基于貪婪策略整體分布優化算法的0－1背包問題求解

薛翠平，劉靜宜，肖 冬

（1.東北大學理學院，遼寧 沈陽110004；2.東北大學信息科學與工程學院，遼寧 沈陽110004）

0 引言

20世紀50年代末，Daunts首次提出0－1背包問題（Knapsack problem），它是一類非常經典的Np問題［1］，在實際生活中，網絡資源分配問題、調運裝載、生產安排、信息加密等問題都能建出0－1背包問題的數學模型［2－4］，因此對該問題的研究在理論上和現實中都具有重要的意義.

0－1背包問題可以簡單描述為：給定n種物品集合N＝｛1，2，…，n｝和一背包.已知物品i的質量為wi（＞0），價值為vi（i＝1，2，…，n），背包容量為c.求最優裝包方案（x1，x2，…，xn），xi∈｛0，1｝（xi＝0表示不把第i個物品放入背包，xi＝1表示把第i個物品裝入背包），使背包獲得的價值達到最大.在選擇裝包物品時，不能將物品裝入背包多次，也不能將物品分割裝入，數學模型如下：

許多學者對該問題進行了行之有效的研究，主要包括適用于小規模問題的分支限界法、遞歸法、回溯法、動態規劃法等及適用于大規模問題的智能計算方法（遺傳算法、人工魚群算法、模擬退火算法、粒子群算法、免疫算法等［5－8］）.目前這方面的文獻很多，每種方法各有優劣，但總體來說思想還是比較復雜.

1 算法

整體分布優化算法是粒子群優化算法衍生出來的一種新智能優化算法［9］，本文將貪婪思想嵌入到整體分布優化算法中，得到基于貪婪策略的整體分布優化算法.該算法主要具有結構簡單、實現容易、代碼較少和參數少的優點.種群相對價值較高，程序對內存要求較小，種群的個體可以逐一形成，不需要存儲.算法的基本思想是首先在定義域范圍內隨機產生一個初始種群，在種群中找到最優粒子，然后直接在最優粒子附近由柯西分布產生新的種群，周而復始，直到達到最大的迭代次數為止.決定該算法性能的因素主要產生種群的概率分布形式及其參數的選取，算法的收斂策略及其對應參數的選取.根據貪婪思想，將所有物品按照價值密度（每種物品的價值系數vi與其質量wi的比值）從大到小編號.將相應的vi和wi按照價值密度順序大小做相應的調整.新的問題記為：

以下內容是在新問題的基礎上求解的：首先，整體分布式優化算法需要編碼，在0－1背包問題中只存在裝入和不裝入2種情況，所以算法采用二進制編碼，0表示不裝入，1表示裝入，編碼長度為所需裝入物品的數量；其次，整體分布優化算法需要適應度函數，這里我們把適應度函數定義為0－1背包問題的目標函數

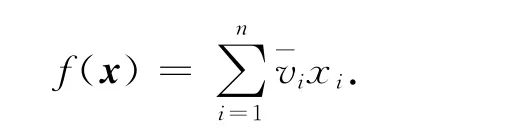
整體分布優化算法的初始種群通過下面的子算法1給出.

算法1 初始種群的產生，種群規模為m，變量的維數為n

Step 2 將第一步產生的解轉換成可行解，思想為貪婪思想，即盡量將下角標小的物品裝入背包.比如，當前已經考慮到第k個物品，若x［i］［k］＝0，則第k個物品不裝入背包；若x［i］［k］＝1，考慮將第k個物品裝入背包，看看是否超重，若不超重，則裝入，否則，該物品不應裝入背包，置x［i］［k］＝0.

下面給出完整的整體分布式優化算法.

算法2 貪婪策略整體分布優化算法

Step 1：初始化.在整個定義域內按照子算法1產生初始種群，同時初始化柯西分布的半徑為覆蓋整個定義域的0.5倍，初始化參數.柯西分布尺度參數γ＝0.1，種群直徑遞減率α＝0.93，停滯次數β＝9，最大迭代次數10 000或者種群直徑的標度小于0.000 001，種群的規模為70.

Step 2：計算種群中每個個體的適應度值，找出本次最好的個體并與上次的最好個體比較，如果好于上次，則進行替換，種群的直徑保持不變.

如果差于上次的最好個體，則保留上次，同時使停滯次數減1，若停滯次數為0，則使種群直徑縮減為原來直徑的0.93，同時使停滯次數變為9；若停滯次數不為0，則保持原來的種群直徑不變.迭代次數減1.

Step 3：以已經找到的最好個體的坐標為中心，用柯西分布產生新的種群.

Step 4：如果當前迭代次數達到了預先設定的最大次數或種群直徑的標度小于0.000 001，則停止迭代、輸出最優解、否則轉到Step 2.

2 實例

為了驗證本文算法在求解0－1背包問題上的有效性，這里引用文獻［7］中的3個實例，3個例子的規模從小到大倍增，通過3個實例比較了幾種算法結果的優劣及本文算法點列的收斂趨勢及速度.

例1 物品個數n＝20，物品價值集合P＝｛92，4，43，83，84，68，92，82，6，44，32，18，56，83，25，96，70，48，14，58｝，物品質量 集 合W ＝｛44，46，90，72，9l，40，75，35，8，54，78，40，77，15，61，17，75，29，75，63｝，背包容量C＝878，具體結果見表1和圖1.

表1 例1中7種算法的最好結果對比

例2 物品個數n＝50，物品價值集合P＝｛220，208，195，192，180，180，165，162，160，158，155，130，125，122，120，118，115，110，105，101，100，100，98，96，95，90，88，82，80，77，75，73，72，70，69，66，65，63，60，58，56，50，30，20，15，10，8，5，3，1｝，物品質量集合W ＝｛80，82，85，70，72，70，66，50，55，25，50，55，40，48，50，32，22，60，30，32，40，38，35，32，25，28，30，22，25，30，45，30，60，50，20，65，20，25，30，10，20，25，15，10，10，10，4，4，2，1｝，背包容量C＝1 000，具體結果見表2和圖2.

圖1 例1中本文算法1次執行過程不同初始點向最優點收斂圖形

表2 例2中7種算法的最好結果對比

例3 隨機產生的實例，n＝100，物品價值集合P＝｛68，101，125，159，65，146，28，92，143，37，5，154，183，117，96，127，139，113，100，95，12，134，65，112，69，45，158，60，142，179，36，43，107，143，49，6，130，151，102，149，24，155，41，177，109，40，124，139，83，142，116，59，131，107，187，146，73，30，174，113，9l，37，168，175，53，151，125，31，192，138，88，184，110，159，189，147，31，169，192，56，160，138，84，42，151，37，21，22，200，85，135，200，139，189，68，94，84，22，18，115｝，物 品 的 質 量 集 合W ＝｛42，35，70，79，63，6，82，62，96，28，92，3，93，22，19，48，72，70，68，36，4，23，74，42，54，48，63，38，24，30，17，9l，89，4l，65，47，91，71，7，94，30，85，57，67，32，45，27，38，19，30，34，40，5，78，74，22，25，7l，78，98，87，62，56，56，32，5l，42，67，8，8，58，54，46，10，22，23，7，14，l，63，11，25，49，96，3，92，75，97，49，69，82，54，19，1，28，29，49，8，11，14｝，背包容量C＝2 010，具體結果見表3和圖3.

表3 例3中7種算法的最好結果對比

圖2 例2中本文算法1次執行過程不同初始點向最優點收斂圖形

圖3 例3中本文算法1次執行過程不同初始點向最優點收斂圖形

由表1—3可以看出，本文基于貪婪策略整體分布優化算法對3個算例求解的最好結果與最優解優于其他幾個算法.由圖1—3又可以看出本文算法向最優點收斂的速度非常快.

3 結論

本文程序都是用C＋＋語言編寫，每個實驗均從不同的隨機初始種群運行10次，整體分布優化算法與其他算法相比，取得了較好的效果，不但取得了最好的優化效果，而且優化結果非常穩定，每次優化結果的值變化不大.說明整體分布優化算法對0－1背包問題是可行的，為有效求解此類問題提供了一種新的可行方法，同時也拓展了整體分布優化算法的應用領域.

［1］SYSLO M M.Discrete optimization algorithm［M］.New Jersey：Prentice－Hall，1983：118－165.

［2］SOOJEONG CHOI，SUNJU PARK，HAK－MAN KIM.The application of the 0－1knapsack problem to the load－shedding problem in microgrid operation［J］.Communications in Computer and Information Science：Control and Automation，and Energy－System Engineering，2011，256（1）：227－234.

［3］NAONORI KAKIMURA，KAZUHISA MAKINO，KENTO SEIMI.Computing knapsack solutions with cardinality robustness［J］.Lecture Notes in Computer Science Algorithms and Computation，2011，7074：693－702.

［4］LAIH C S，LEE J Y，HAM L，et.A linearly shift knapsack public－key cryptosystem［J］.IEEE Journal Selected Areas Communication，1989，7（4）：534－539.

［5］秦玲，白云，章春芳，等.解0－1背包問題的蟻群算法［J］.計算機工程，2006，3（6）：212－214.

［6］沈顯君，王偉武，鄭波盡，等.基于改進的微粒群優化算法的0－1背包問題求解［J］.計算機程，2006（18）：23－24，38.

［7］王秋芬，梁道雷.一種求解0－1背包問題的啟發式遺傳算法［J］.計算機應用與軟件，2013，30（2）：33－37，57.

［8］賀毅朝，劉坤起，張翠軍，等.求解背包問題的貪心遺傳算法及其應用［J］.計算機工程與設計，2007，28（11）：2655－2657.

［9］余炳輝.整體分布優化算法研究及應用［M］.成都：西南交通大學出版社，2012：129－140.