賦廣義Orlicz范數(shù)Orlicz函數(shù)空間的完全k－凸性

程亞煥，段麗芬，左明霞

（1.通化師范學(xué)院數(shù)學(xué)學(xué)院，吉林 通化134002；

2.哈爾濱理工大學(xué)應(yīng)用科學(xué)學(xué)院，黑龍江 哈爾濱150080）

1955年，文獻(xiàn)［1］引進(jìn)了完全k－凸的概念.設(shè)k≥2為正整數(shù)，Banach空間X 稱(chēng)為完全k－凸（FKR）的是指蘊(yùn)含｛xn｝為Cauchy序列.同時(shí)證明了完全k－凸的Banach空間是嚴(yán)格凸且自反的.1989年，文獻(xiàn)［2］獲得了賦Orlicz范數(shù)Orlicz空間完全k－凸的判據(jù).1998年，文獻(xiàn)［3］找到了賦Luxemburg 范數(shù)Orlicz空間完全k－凸的條件.本文給出賦廣義Orlicz范數(shù)Orlicz空間完全k－凸的判別準(zhǔn)則.

1 定義及符號(hào)

定義1［4］若M 是非負(fù)凸連續(xù)偶函數(shù)，且u＝0?M（u）＝0，則映射M：R→［0，∞）稱(chēng)為Orlicz函數(shù)；滿(mǎn)足的Orlicz函數(shù)稱(chēng)為N－函數(shù).

定義M（u）的余函數(shù)

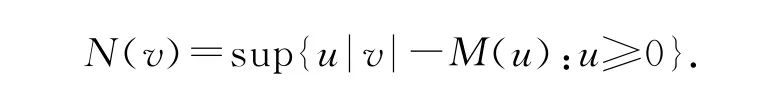
設(shè)（G，Σ，μ）為一有限無(wú)原子測(cè)度空間，L0為G 上的可測(cè)實(shí)函數(shù)全體.泛函x∈L0稱(chēng)為x 關(guān)于M 的模.在

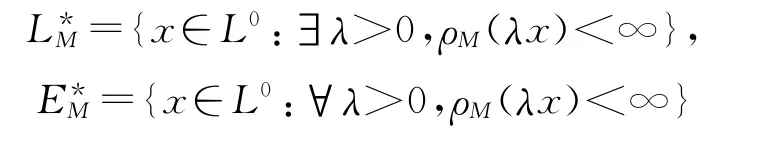
上定義Orlicz范數(shù)

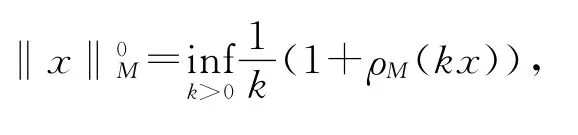
Luxemburg范數(shù)

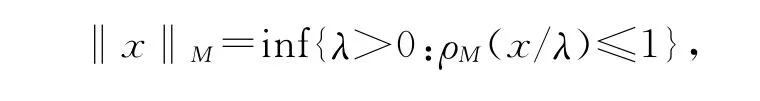
及廣義Orlicz范數(shù)

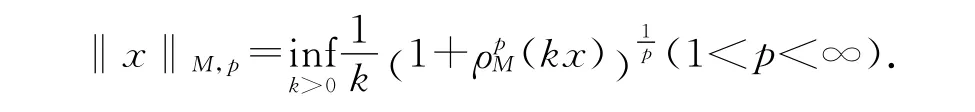
它們均成為Banach空間［5］.在廣義Orlicz范數(shù)下，分別簡(jiǎn)記

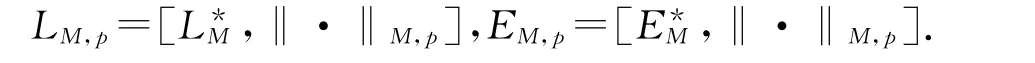
在處理Orlicz函數(shù)空間時(shí)，“M∈Δ2”表示M（u）對(duì)較大的u滿(mǎn)足Δ2條件，即存在K＞2和u0≥0使得M（2u）≤KM（u）（u≥u0）.

2 主要結(jié)果

定理1 設(shè)M 是N－函數(shù)，則對(duì)任何1＜p＜∞，LM，p完全k－凸（k≥2為正整數(shù)）的充要條件是M∈Δ2∩Δ

2且M 嚴(yán)格凸.

證明 必要性.因完全k－凸的Banach空間是自反的，且嚴(yán)格凸，由文獻(xiàn)［6］定理5和文獻(xiàn)［7］定理

3.3.4 可直接得到結(jié)論.

充分性.只需證明條件滿(mǎn)足時(shí)，LM，p完全2－凸即可.事實(shí)上，設(shè)｛xn｝∞n＝1?B （LM，p），設(shè)kn＞1滿(mǎn)足考慮到M∈Δ及文獻(xiàn)［8］的定理2，｛kn｝有界.記k′＝inf｛kn｝，k″＝sup｛kn｝，則0＜k′≤k″＜∞，進(jìn)而再利用M 的凸性及M ∈Δ2，存在δ＞0，使得

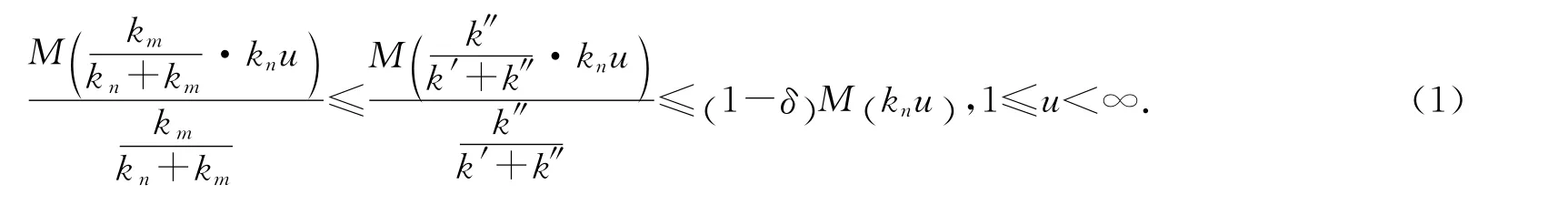
下面分三步證明｛xn｝為Cauchy序列.

第一步 證明｛xn｝∞n＝1?B（LM，p）具有等度絕對(duì)連續(xù)范數(shù).若不然，存在ε0＞0，對(duì)任何η＞0，都存在無(wú)窮多個(gè)n和en?G，μen＜η，使得

記

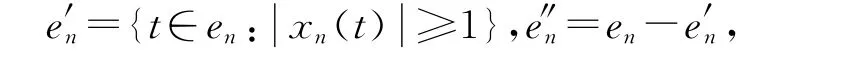
則

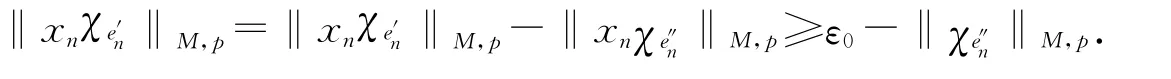
因M∈Δ2，對(duì)任何ε＞0，存在ξ＞0，只要

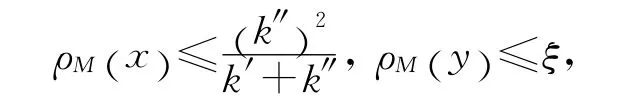
就有

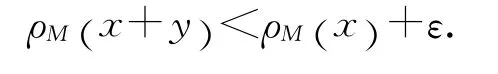
因當(dāng)n，m→∞時(shí)，

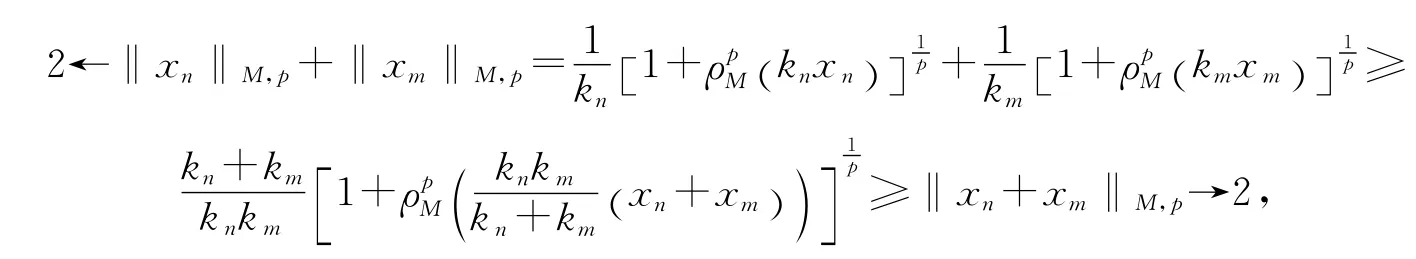
可取定正整數(shù)m，使得當(dāng)n＞m 時(shí)，

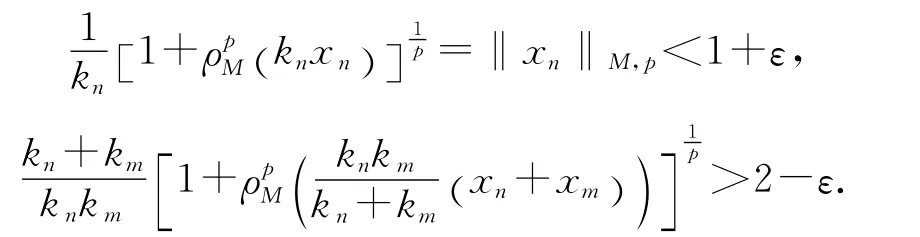
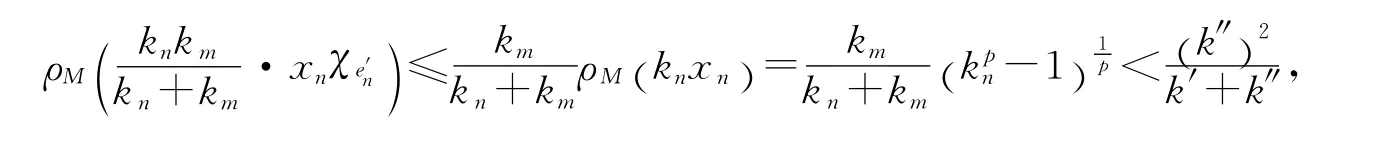
從而

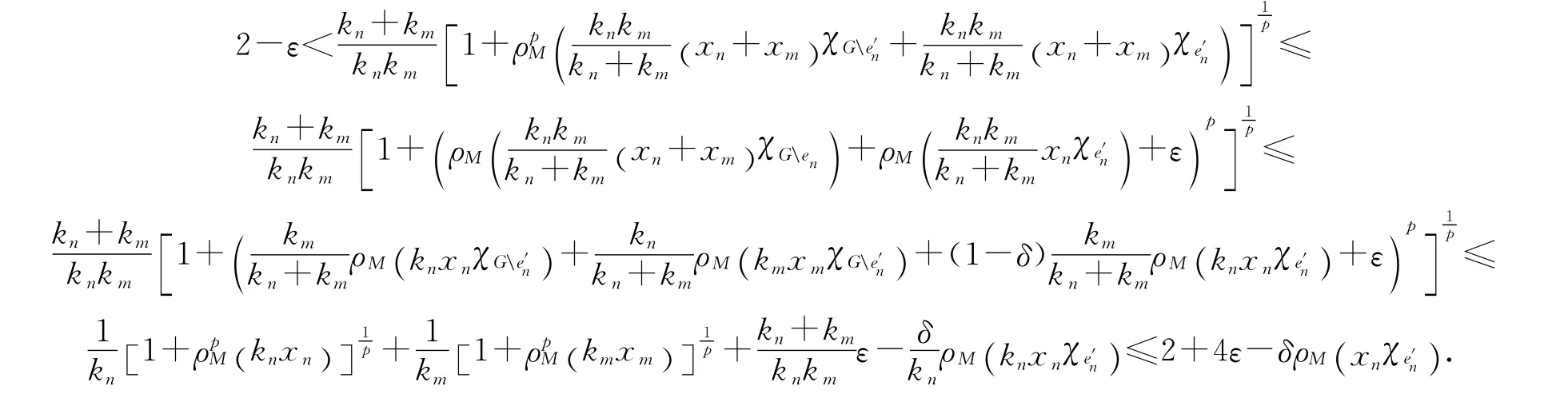
注意到M∈Δ2，存在ε′0＞0，使得蘊(yùn)含由（2）式可得2－ε≤2＋4ε－δε′0，或這與ε的任意性矛盾.從而證明了｛xn｝∞n＝1?B（X）具有等度絕對(duì)連續(xù)范數(shù).

第二步 證明knxn－kmxm→—μ 0（n，m→∞）.若不然，不妨設(shè)對(duì)所有正整數(shù)n，m 不等式

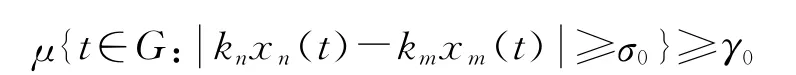
成立.其中σ0，γ0為正常數(shù).因M ∈，據(jù)文獻(xiàn)［8］可知｛kn｝n∞＝0有界，從而｛ρM （knxn）｝n∞＝0有界.設(shè)ρM（knxn）≤d（n＝0，1，2，…），D＝記

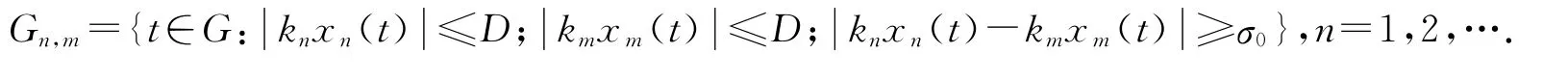
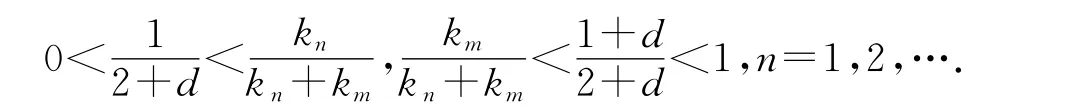
利用文獻(xiàn)［9］中性質(zhì)1.4，存在δ0＞0，使得對(duì)一切u，v及只要便有M（αu＋（1－α）v）≤（1－δ0）［αM（u）＋（1－α）M（v）］.注意到和

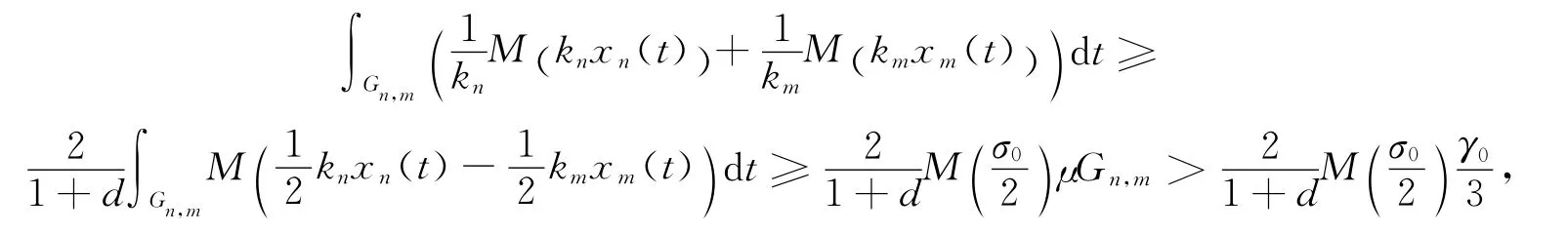
再利用Minkowsky不等式可得

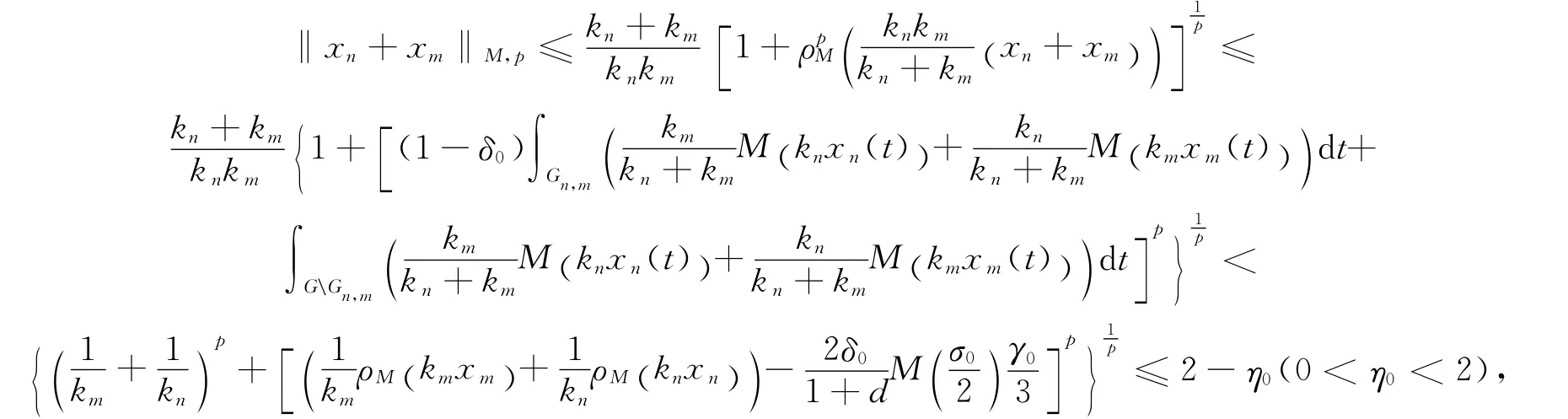
這與‖xn＋xm‖M，p→2（n→∞）矛盾.

第三步 證明｛xn｝為Cauchy序列.事實(shí)上，因則｛knxn｝依測(cè)度收斂，設(shè)

對(duì)｛xn｝的任意子列，相應(yīng)｛kn｝的子列都存在收斂子列，仍記為｛kn｝.設(shè)kn→k0（n→∞），則

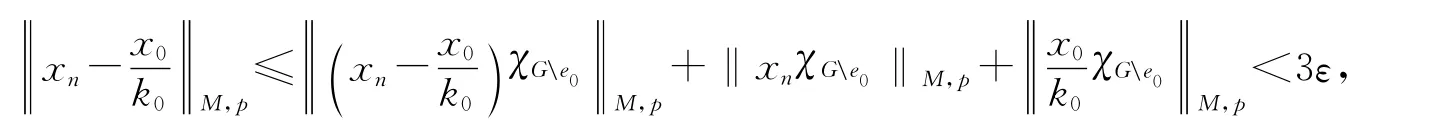
［1］FAN K，GLICKSBERG I.Fully convex normed linear spaces［J］.Proc Nat Acad Sci U S A，1955，41（11）：947－953.

［2］王廷輔，張?jiān)品澹醣Ｏ?Orlicz空間的Fully K 凸［J］.哈爾濱師范大學(xué)自然科學(xué)學(xué)報(bào)，1989，5（3）：19－21.

［3］CHEN SHUTAO，LIN BOLU，YU XINTAI.Rotund reflexive Orlicz spaces are fully convex［J］.Comtemporary Math，1998，85：79－86.

［4］張靜，段麗芬，左明霞.賦廣義Orlicz范數(shù)Orlicz序列空間的k－端點(diǎn)和k－強(qiáng)端點(diǎn)［J］.東北師大學(xué)報(bào)：自然科學(xué)版，2014，46（4）：42－47.

［5］CUI Y A，DUAN L F，HUDZIK H，et al.Basic theory of p－amemiya norm in Orlicz spaces（1≤p≤∞）：extreme points and rotundity in Orlicz spaces endowed with these norms［J］.Nonlinear Analysis：Theory，Methods ＆ Applications，2008，69（5／6）：1796－1816.

［6］李小彥，崔云安.賦P－Amemiya范數(shù)Orlicz空間的對(duì)偶空間［J］.哈爾濱理工大學(xué)學(xué)報(bào)，2011，16（1）：110－112.

［7］段麗芬.Orlicz空間和商空間的若干幾何性質(zhì)［D］.哈爾濱：哈爾濱理工大學(xué)，2004.

［8］許晶，崔云安，莊彩彩.賦廣義Orlicz范數(shù)的Orlicz空間中kx的兩個(gè)特征［J］.通化師范學(xué)院學(xué)報(bào)，2010，31（12）：14－15.

［9］CHEN SHUTAO.Geometry of Orlicz spaces［M］.Warszawa：Dissertations Math，1996：6－7.