優勢決策信息系統規則獲取方法及應用

索中英，程嗣怡，袁修久，李彥明

(1.空軍工程大學 理學院，陜西 西安710051;2.空軍工程大學 航空航天工程學院，陜西 西安710038)

0 引言

原始的粗糙集理論并不能從多準則(描述偏好程度的有序屬性值)有序分類問題的決策表中提取所有的基本知識［1］，然而在很多實際問題中，考慮屬性的有序性是很重要的。例如對于威脅等級分類中不同目標的工作狀態、距離等屬性，不僅要考慮屬性的不可區分性或相似性，更應考慮屬性對于威脅等級分類的有序性。

Greco 等提出多準則有序分類問題的優勢粗糙集方法，使用占優和不可區分結合的二元關系來建立粗糙近似［2-3］。在針對優勢關系粗糙集模型的研究中，根據優勢關系獲取決策規則是研究的熱點之一。Greco 等優勢粗糙集方法給出了確定D≥、可能D≥、確定D≤、可能D≤、近似D≥≤5 種決策規則形式［4-5］，文獻［6］提出了“↑”和“↓”描述符，并給出了“↑”和“↓”兩種可信規則形式，文獻［7］通過語義計算方法給出了3 種規則形式。從這些文獻可以看出，多數規則都是從Greco 形式中演變而來，用于解決不同應用方面的問題，但這些規則形式僅能從有限數據中提取有限決策規則，這就給決策過程帶來了困難。文獻［8］研究協調優勢決策信息系統的規則獲取方法，該方法試圖通過少數樣本數據，獲取涵蓋目標條件屬性所有取值的確定性規則，其規則的正確性是值得商榷的，文獻［8］在決策規則獲取方法中設Et=∧Ft，是以屬性向量(對象屬性取值的有序數組)為單位取小，而在針對目標威脅評估的實例中是以單個屬性為單位取小，并且兩種取法均有其不足之處，以屬性向量為單位取小，作為取得該決策的最小屬性值，要求取得該決策的屬性值必須大于等于該最小屬性值，此種做法要求實例數據必須包含取得各類決策的最小屬性取值樣本，顯然不具通用性;以單個屬性為單位取小則極易出現不同決策的最小屬性取值相同的情況，如文獻［8］實例中E1= E2= {(1，1，1，1，1)}，在此基礎上得到(1，1，1，1，1)→d=1 而不是(1，1，1，1，1)→d =2 是缺少依據的，并且在極端的情況下極有可能出現各類決策的最小屬性取值均相同的情況。綜上所述，文獻［8］中方法易導致所獲取規則正確率較低。

此外在目標威脅評估等實際問題中，所面對的信息系統不僅是基于優勢關系的，而且是不協調的。Greco 等在2000年提出一種基于優勢關系下的可變一致性模型(VC-DRSA)［9］，該模型設定了一個信任度，并利用具有“自反”和“傳遞”特性的優勢關系來解決多屬性決策問題。文獻［10 -11］在基于優勢關系下的信息系統中引入了協調近似空間的概念，分別討論了分配約簡和分布約簡，進一步豐富了基于優勢關系下不協調決策信息系統的研究。

然而通過分析發現文獻［9 -11］中關于不協調優勢決策信息系統的研究均是在“承認引起優勢決策信息系統不協調的對象存在是合理的”基礎上展開的。本文認為要從不協調優勢決策信息系統中提取規則，首先應依據在優勢決策信息系統中，相對于決策屬性而言，條件屬性值是效益型還是成本型，借助一定的方法剔除不合理對象而后提取其決策規則。

1 相關概念及理論

1.1 優勢決策信息系統及其屬性約簡

定義1［1］稱{U，A，F，d}是決策信息系統，其中U={x1，x2，…，xn}為對象集，U 中的每個元素xi(i≤n)稱為一個對象。A ={a1，a2，…，am}為屬性集，A 中的每個元素al(l≤m)稱為一個屬性。F ={fl:U→Vl(l≤m)}為U 與A 之間的關系集，其中Vl為al(l≤m)的值域。d:U→Vd為決策，Vd取有限值。

定義2 設{U，A，F，d}為決策信息系統，R≤A=其中稱為決策信息系統的優勢關系，此時該決策信息系統稱為優勢決策信息系統。

定義3 設{U，A，F，d}為決策信息系統，給出優勢關系R≤B，若R≤B=R≤A，稱B 為優勢決策協調集。若B 為優勢決策協調集，且B 的任何真子集都不是優勢決策協調集，則稱B 為優勢屬性約簡集，簡稱優勢約簡集。

定理1 設{U，A，F，d}是優勢決策信息系統，對于任意Dd＜∈Q，屬性約簡集B 滿足B∩Dd＜≠?.

1.2 基于粗糙集的全序化方法

粗糙集方法通過關系模型得到優勢信息系統中的對象之間的排序［12-13］。

若(xi，xj)∈R≤B，它等價于B，記作若記為

定理2 若B?A，R≤B=R≤A，則xi≤Bxj當且僅當xi≤Axj.

通過粗糙集方法實現優勢決策信息系統中的對象排序［12］，步驟如下:

1)計算優勢決策信息系統的辨識矩陣Q，而后依據定理1 獲得該決策信息系統的屬性約簡集。

2)針對約簡的優勢決策信息系統，求取所有的［xi］≤B(i≤n)，對于，利用包含度計算屬性集B 條件下，對象xi優于xj的程度，

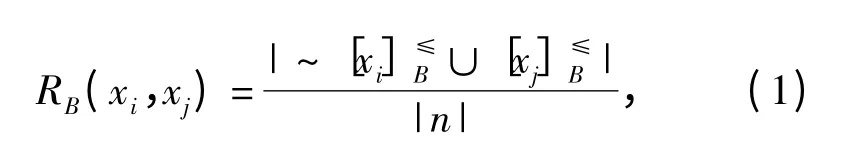
式中:|·|表示集合元素的個數;n 表示對象的個數。進一步獲得對象之間的優勢矩陣

3)利用算術平均得到對象xi在屬性B 下的綜合優勢度

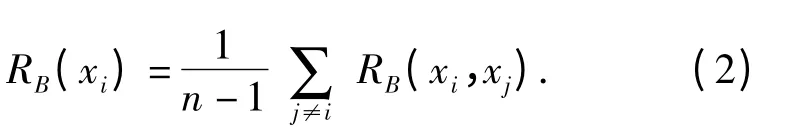
RB(xi)的值越大，則對象xi越具有優勢，因此按照RB(xi)由大到小的順序即可將對象由優到劣排序。

定義4 對任意的x，y∈U，如果x≤y 或x≥y之一成立時，則稱x、y 是可比的，否則稱為不可比的。

由粗糙集方法可以得到對象的某種排序，并且無論約簡屬性集是否唯一，得出的排序在可比較的對象上是一致的。

2 優勢決策信息系統的規則獲取方法

借助粗糙集方法，利用優勢決策信息系統中的條件屬性集能夠實現對象的優劣排序，在排序的基礎上綜合考慮決策屬性，則可剔除不協調對象，將不協調決策信息系統轉化為協調決策信息系統。

因此接下來針對協調決策信息系統{U，A，F，d}，討論其決策規則獲取方法。

設Vl=Vd=V，條件屬性集的取值域與決策屬性的取值域相同。

設Vm={(u1，u2，…，um)|ul∈V(l≤m)}，對于(u1，u2，…，um)∈Vm，(v1，v2，…，vm)∈Vm，記(u1，u2，…，um)∧(v1，v2，…，vm)=(u1∧v1，u2∧v2，…，um∧vm)，(u1，u2，…，um)∨(v1，v2，…，vm)=(u1∨v1，u2∨v2，…，um∨vm)，其中ul∧vl和ul∨vl分別表示取ul與vl中的最小值和最大值。

假定協調優勢決策信息系統{U，A，F，d}是有限值域的，Vl=Vd=V={1，2，…，r}，l≤m.

設Dt={xi|d(xi)=t}，t≤r 表示決策目標為t的對象集合，Ft={F(xi)|xi∈Dt}，t≤r 表示決策目標為t 的對象的屬性值集合，記Ft中存在可比較對象的對象集合為Gt，不存在可比較對象的對象集合為Mt. Et=∧Gt=∧{F(xi)∈Gt|xi∈Dt}，t≤r 表示決策目標為t 的屬性值中取小值，Ht= ∨Gt=∨{F(xi)∈Gt|xi∈Dt}，t≤r 表示決策目標為t 的屬性值中取大值。

1)假設決策目標值越大時，對象的屬性向量越大，即屬性值是效益型時，可以得到以下確定性決策規則:

r1:若F(x)≤F(xi)∈(H1∨M1)，則d(x)=1;

r2:若(F(x)≥F(xi)∈Et)∧(F(x)≤F(xi)∈Ht)，1 ＜t ＜r，或者F(x)=F(xi)∈Mt，則d(x)=t;

r3:若F(x)≥F(xi)∈(Er∨Mr)，則d(x)=r.

此外可得到部分確定性規則:

r4:若F(x)＜(Ht∨Mt)，t ＜r，則d(x)=1∨2∨…∨t;

r5:若F(x)＞F(xi)∈(Et-k∨Mt-k)，并且F(x)＜F(xi)∈(Ht∨Mt)，則d(x)=t-k∨t -k +1∨…∨t;

r6:若F(x)＞F(xi)∈(Et∨Mt)，t ＞1，則d(x)=t∨t+1∨…∨r.

2)假設決策目標值越大時，對象的屬性向量越小，即屬性值是成本型時，可以得到以下確定性決策規則:

r1* :若F(x)≥F(xi)∈(E1∨M1)，則d(x)=1;

r2* :規則不變;

r3* :若F(x)≤F(xi)∈(Hr∨Mr)則d(x)=r.

此外可得到部分確定性規則:

r4* :若F(x)＞(Et∨Mt)，t ＜r，則d(x)=1∨2∨…∨t;

r5* :若F(x)＜F(xi)∈(Ht-k∨Mt-k)，并且F(x)＞F(xi)∈(Et∨Mt)，則d(x)=t -k∨t -k+1∨…∨t;

r6* :若F(x)＜F(xi)∈(Ht∨Mt)，t ＞1，則d(x)=t∨t+1∨…∨r.

3)假設當屬性取某個值、某些值或屬于某個區間時，決策目標值最大，則需要結合實際問題背景，依據屬性值的偏離程度，將屬性值轉化為效益型或成本型，而后借助效益型或成本型的規則獲取方法，獲得決策規則。

3 實例分析

雷達對抗目標威脅等級評估優勢決策信息系統(U，A，F，d)如表1所示，其中U={x1，x2，x3，x4，x5，x6}為目標雷達對象集，A ={a1，a2，a3，a4，a5，a6}為屬性集，雷達對抗目標威脅評估信息系統中屬性取值可能是有限離散值、連續數值，也可能是語言值。本實例已將其統一處理為效益型離散取值屬性，優劣排序為3?2?1，F ={fl:U→Vl，al∈A}為目標雷達對象與屬性之間的關系集，Vl的取值見表1，由于所以該雷達對抗目標威脅等級評估信息系統為不協調優勢決策信息系統，其對應的辨識矩陣如表2所示。

表1 雷達對抗目標威脅評估優勢決策信息系統Tab.1 Dominance decision-making information system for target threat assessment

表2 威脅評估優勢決策信息系統的辨識矩陣Tab.2 Discernibility matrix of dominance decision-making information system for threat assessment

3.1 基于粗糙集的協調化處理

首先在決策辨識矩陣中提取非空決策辨識集，而后依據定理1 可得雷達目標威脅評估優勢決策信息系統的屬性約簡為B={a1，a2，a3，a5，a6}.

對于約簡后的優勢決策信息系統有

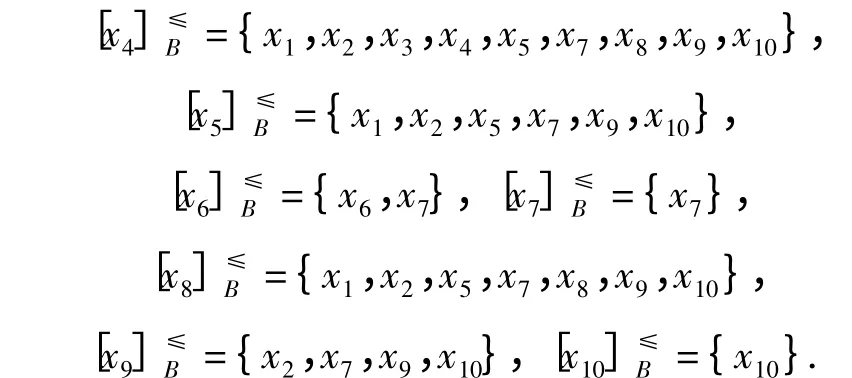
由(1)式可得到雷達目標的優勢矩陣

由(2)式計算目標xi威脅的綜合優勢度RB(xi)為:RB(x1)≈0.83，RB(x2)≈0.78，RB(x3)≈0.52，RB(x4)≈0.43，RB(x5)≈0.67，RB(x6)≈0.79，RB(x7)≈0.88，RB(x8)≈0.6，RB(x9)≈0.78，RB(x10)≈0.88.

根據RB(xi)由大到小，得出目標威脅等級次序為:x7≈x10?x1?x6?x2≈x9?x5?x8?x3?x4，結合決策屬性可以看出目標x7和x8威脅等級決策是不合理的，因此將優勢決策信息系統中的對象x7和x8剔除。

3.2 目標威脅評估規則提取

由對象U={x1，x2，x3，x4，x5，x6，x9，x10}構成的協調優勢決策信息系統中，D1={x3，x4}，D2={x2，x5，x6，x9}，D3={x1，x10}，F1={(2，1，2，2)，(1，1，1，2)}，F2={(2，3，2，3)，(2，2，2，2)，(3，1，3，1)，(2，3，2，3)}，F3={(2，2，3，3)，(2，3，3，3)}，E1=(1，1，1，2)，H1=(2，1，2，2)，E2=(2，2，2，2)，H2=(2，3，2，3)，M2=(3，1，3，1)，E3=(2，2，3，3)，H3=(2，3，3，3)，于是有確定性規則，共17 條:

r1:當F(x)≤H1(x)時，d(x)=1;

r2:當E2(x)≤F(x)≤H2(x)或F(x)=M2(x)時，d(x)=2;

r3:當F(x)≥E3(x)時，d(x)=3.

而后在其余64 類條件屬性中，尋找部分確定性規則:

r4:當F(x)＜H2(x)或F(x)＜M2(x)時，d(x)=1∨2;

r5:當F(x)＞E2(x)或F(x)＞M2(x)時，d(x)=2∨3.

依據以上規則可以得到目標威脅評估的17 條確定規則和40 條部分確定規則，如表3所示。

表3 目標威脅評估規則庫Tab.3 Rules of target threat assessment

4 結論

本文圍繞優勢決策信息系統的規則獲取方法展開研究，具體完成以下主要工作:

1)給出優勢決策信息系統的決策辨識集和決策辨識矩陣的定義，以及尋找屬性約簡集的方法。

2)在屬性約簡的基礎上，利用基于優勢關系的粗糙集方法實現對象的優劣排序，綜合考慮決策屬性，剔除不協調對象，將不協調優勢決策信息系統轉化為協調優勢決策信息系統。其中基于優勢關系的優劣排序方法與其他排序方法得出的結果［13］，在可比較的對象上完全相同，這一點說明了利用該方法進行優劣排序的有效性。

3)提出協調優勢決策信息系統的規則獲取方法，該方法在充分挖掘決策信息系統中蘊含信息的同時，確保規則的正確性。利用文中方法得到的規則與利用基本粗糙集方法僅可以得到的8 條規則一致，此外文獻［8］中利用10 個樣本得到全部條件屬性取值的108 條規則是不甚合理的，本文區分確定性規則和部分確定性規則，保證了規則的正確性和合理性。

準確對多部目標雷達進行威脅等級評估是快速進行干擾決策、合理分配干擾資源，達到最佳干擾效果的重要依據，是電子對抗領域的一個重要研究課題。通過實例分析發現文中方法為雷達目標威脅評估提供了新的方法和思路，此外該方法具有普適性，可以為解決現實生活中大量面對的屬性含有“偏好信息”的決策問題提供參考。

References)

［1］Pawlak Z. Rough sets［J］. International Journal of Information and Computer Sciences，1982，11(5):341 -356.

［2］Greco S，Matarazzo B，Slowinski R. A new rough set approach to multicriteria and multiattribute classification［C］∥Proceedings of the First International Conference on Rough Sets and Current Trends in Computing. Berlin:Springer-Verlag，1998，1424:60 -67.

［3］Greco S，Matarazzo B，Slowinski R. Rough approximation of a preference relation by dominance relation［J］. European Journal of Operational Research，1999，117(2):63 -83.

［4］Greco S，Matarazzo B，Slowinski R. Rough approximation by dominance relation［J］. International Journal of Intelligent Systems，2002，17(2):153 -171.

［5］Greco S，Matarazzo B，Slowinski R. Rough sets theory for multicriteria decision analysis［J］. European Journal of Operational Research，2001，129(1):1 -47.

［6］Yang X B，Xie J，Song X N，et al. Credible rules in incomplete decision system based on descriptors［J］. Knowledge-based Systems，2009，22(1):8 -17.

［7］Liou J J H. A novel decision rules approach for customer relationship management of the airline market［J］. Expert System with Application，2009，36(3):4374 -4381.

［8］蔡佳，胡杰，黃長強. 協調優勢粗糙集方法及其在UVAV 目標威脅評估中的應用［J］. 系統工程理論與實踐，2012，32(6):1377 -1384.CAI Jia，HU Jie，HUANG Chang-qiang. A consistent dominance rough sets method and its application in threat assessment of UCAV＇s targets［J］. Systems Engineering-Theory ＆ Practice，2012，32(6):1377 -1384.(in Chinese)

［9］Greco S，Matarazzo B，Slowinski R，et al. Variable consistency model of dominance-based rough sets approach［C］∥Proceedings of the Second International Conference on Rough Sets and Current Trends in Computing. Banff，Canada:Berlin:Springer-Verlag Berlin Heidelberg，2001:170 -181.

［10］徐偉華，張文修. 基于優勢關系下的協調近似空間［J］. 計算機科學，2005，32(9):164 -165.XU Wei-hua， ZHANG Wen-xiu. Consistent approxi-mation spaces based on dominance relations［J］. Computer Science，2005，32(9):164 -165.(in Chinese)

［11］徐偉華，張曉燕，蘇雅娟，等. 基于優勢關系下的協調近似空間(續)［J］. 計算機科學，2007，34(3):148 -150.XU Wei-hua，ZHANG Xiao-yan，SU Ya-juan，et al. Consistent approximation spaces based on dominance relations(Ⅱ)［J］.Computer Science，2007，34(3):148 -150. (in Chinese)

［12］索中英，程嗣怡，王星，等. 偏序關系全序化的粗糙集方法在裝備效能評估中的應用［J］. 兵工學報，2009，30(4):509-512.SUO Zhong-ying，CHENG Si-yi，WANG Xing，et al. A totally ordered method of partial order based on rough sets applied to evaluation of equipment effectiveness［J］. Acta Armamentarii，2009，30(4):509 -512.(in Chinese)

［13］張文修，仇國芳. 基于粗糙集的不確定決策［M］. 北京:清華大學出版社，2006.ZHANG Wen-xiu，QIU Guo-fang. Uncertain decision making based on rough sets［M］. Beijing:Tsinghua University Press，2006.(in Chinese)