一種簡化的發射系下SINS/GPS/CNS組合導航系統無跡卡爾曼濾波算法

潘加亮，熊智，王麗娜，郁豐，趙慧，林愛軍

(1.南京航空航天大學 自動化學院，江蘇 南京210016;2.北京航天自動控制研究所，北京100854;3.南京航空航天大學 航天學院，江蘇 南京210016)

0 引言

構建發射慣性系下的捷聯慣導系統/導航星全球定位系統/天文尋航系統(SINS/GPS/CNS)多信息組合導航系統是實現未來高超、空天高動態飛行器高精度導航的有效手段之一［1-2］，而發射慣性系下組合導航系統的核心技術是多信息融合處理方法。針對未來高超、空天飛行器飛行軌跡高動態性和導航系統狀態強非線性等特點，傳統的擴展卡爾曼濾波(EKF)算法因系統模型線性化展開的要求而會影響估計的精度［3］。為此，Julier 等提出的無損卡爾曼濾波(UKF)方法可以有效解決模型線性化展開所帶來的模型不準確這一問題［4-9］，其核心思想是通過利用一系列近似高斯分布的采樣點，通過無跡變換(UT)進行狀態和誤差協方差陣的遞推和更新，不需要對系統非線性方程進行線性化，因而可以有效避免引入線性化誤差，提高導航精度。

但對于高階擴維的多組合導航系統，由于組合系統狀態維數過高，傳統的UKF 算法存在大量采樣粒子計算過程，遞推濾波計算步驟繁瑣、運算復雜等問題，影響系統的實時性，使其不便于工程實現。為此，針對發射慣性系下SINS/GPS/CNS 組合導航系統狀態模型非線性而觀測模型線性的特點，本文設計了一種簡化UKF 算法(SUKF)直接進行導航參數的估計，在算法模型等效原則下可以簡化計算步驟，降低計算的復雜度，提高算法的實時性，同時SUKF算法由于繼承了UKF 算法無需狀態模型一階線性化展開的優點，能獲得比EKF 算法更高精度的導航結果，十分適合算法的工程應用。

1 發射系下組合導航系統SUKF 算法

1.1 組合導航系統數學模型

本文選取發射慣性系作為導航坐標系，SINS/GPS/CNS 組合導航系統相關解算方程如下:

式中:q 為姿態四元數(包括一維標量部分q0和三維矢量部分q1、q2、q3);p 為發射慣性系下的位置值;v 為發射慣性系下的速度值;g 為地球的萬有引力;為發射慣性系相對于載體系的姿態矩陣;為發射慣性系相對于地心慣性系的姿態矩陣;fc為加速度實際測量值;fr為加速度計隨機游走誤差;ωc為角速度實際測量值;ωr為陀螺隨機游走誤差;ωε為陀螺測量噪聲;ωn、fn分別為陀螺和加速度計隨機游走驅動噪聲。

考慮到姿態的變化主要反映在四元數的矢量部分，同時為了減少濾波器的計算量，本文選取方程(1)式中的姿態四元數三維矢量部分(q1、q2、q3)、三維位置矢量p、三維速度矢量v、三維陀螺隨機游走誤差ωr、三維加速度計隨機游走誤差fr作為狀態量構建濾波器狀態方程，狀態量定義:X =［q1q2q3pxpypzvxvyvzωrxωryωrzfrxfryfrz］T，系統白噪聲矢量為

W=［ωεxωεyωεzωnxωnyωnzfnxfnyfnz］T.

選取GPS 和星敏感器分別輸出的位置信息和姿態信息(矢量部分)作為觀測量，則有觀測方程:

式中:qc，13為姿態觀測量的矢量部分;qI，13為慣導系統姿態參數的矢量部分;qε，13為姿態量測噪聲;pc為位置觀測量;pI為慣導系統的位置參數;pε為位置量測噪聲;H=［I6×606×9］;V 為量測噪聲陣。

由上述分析，可以獲得發射系下組合導航系統的狀態方程和量測方程一般形式表示為

式中:狀態量X 維數為15 維;系統噪聲向量W 為9 維;系統量測噪聲向量V 為6 維。

1.2 SUKF 算法實現方案

發射慣性系下的SINS/GPS/CNS 組合導航系統狀態方程具有非線性，基于UT 的UKF 濾波算法是處理非線性問題的一種有效方法［10-14］，傳統UKF算法需要將系統噪聲和量測噪聲都增廣為系統狀態，不失一般性，假設系統狀態維數為n 維，系統狀態噪聲陣為w 維，系統量測噪聲陣為v 維，則增廣后的系統狀態維數將由原來的n 維擴展為n +w +v維，擴維后的系統狀態向量表示如下:

在我國計劃生育的變遷過程中，政策專家發揮了不可替代的作用。傳統媒體報道進一步放大了某些代表學者的聲音，甚至使之成為一類政策主張的“符號”；新媒體則賦予了更多專家以話語權，進一步拓展了他們的話語空間，使得專家學者共同體的話語影響力得到強化。

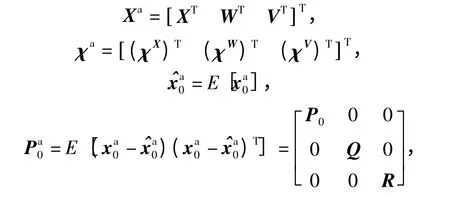
式中:Xa表示擴維后的系統狀態向量;χa為擴維后的狀態對應的采樣點向量;^xa0表示擴維后系統狀態初始均值;Pa0為增廣后的狀態向量初始協方差陣;P0為原狀態向量初始協方差陣;Q 為系統噪聲陣;R為量測噪聲陣。

從擴維后的系統狀態向量可以看出，如果系統自身的狀態噪聲和量測噪聲維數較高，則通過相應的狀態量增廣處理后，進一步增大了狀態維數，從而較大增加了濾波算法運算量，如以本文研究的發射慣性系組合導航系統數學模型為例，按照傳統UKF算法狀態擴維后，其狀態維數將由15 維增加到30 維，從而極大增加了算法的計算量。

為此，在系統狀態自身維數較高的情況下，為減少UKF 算法計算量，結合發射系下組合導航系統量測方程線性的特點，本文設計了一種降維的SUKF實現算法，主要對傳統UKF 算法中^zk/k-1、Pzz和Pxz的計算方法進行簡化，具體簡化部分對應的簡化原理如下:

1.2.1 初始化

基于發射慣性系下系統狀態方程非線性而量測方程線性這一特點，將系統噪聲增廣為狀態向量，而不把量測噪聲增廣為狀態向量，這樣可以有效降低擴維后系統狀態的維數，設簡化后的UKF 算法的增廣狀態向量記為Xa，相應的采樣點向量記為χa，則可得

1.2.2 系統量測方程

由傳統的UKF 算法公式，則有

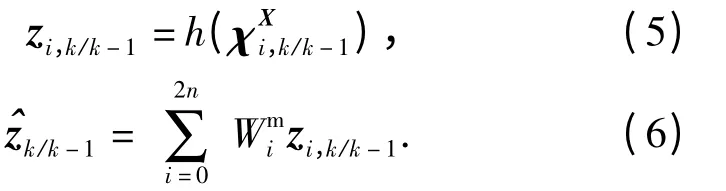
基于發射慣性系下SINS/GPS/CNS 組合導航系統線性量測方程，將(4)式代入(5)式、(6)式得

1.2.3 系統估計誤差方差陣

基于傳統UKF 算法模型有

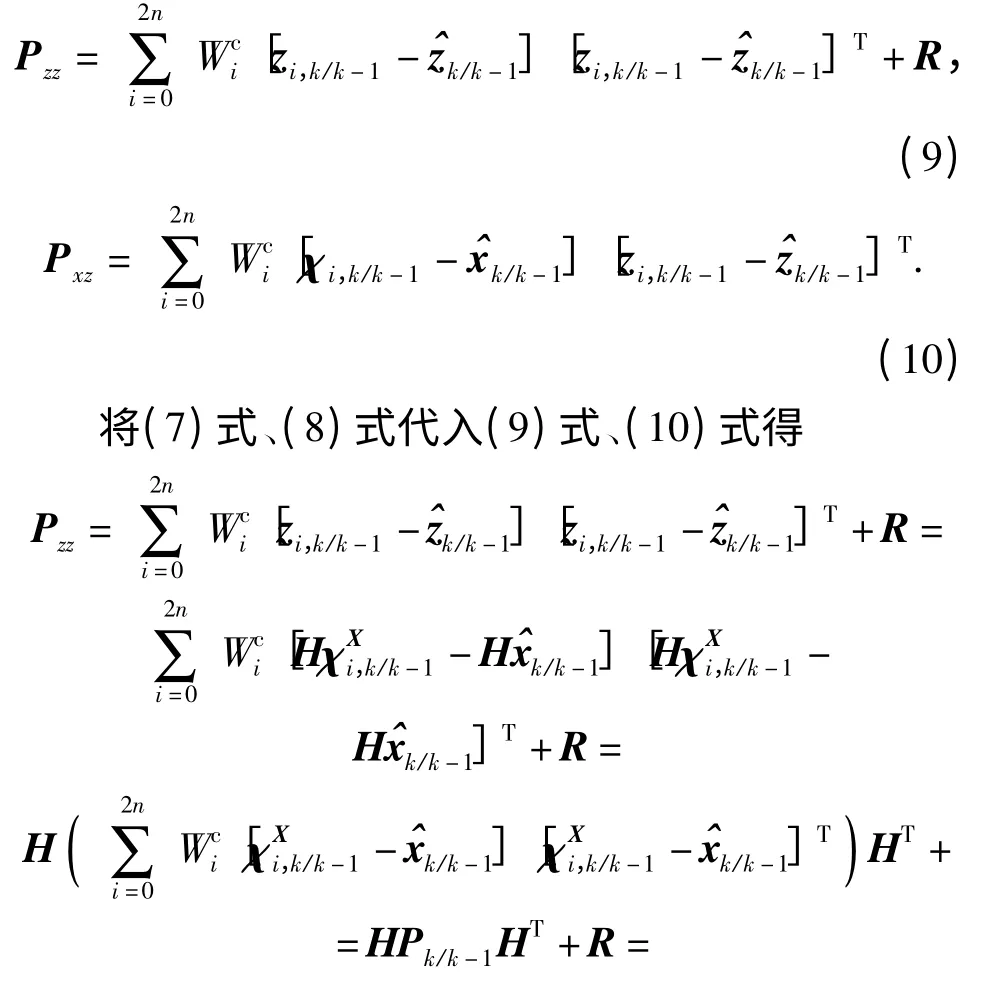
式中:R 表示系統量測噪聲陣;PA1k/k-1表示由Pk/k-1的前六行與前六列構成的分塊矩陣;表示由Pk/k-1的前十五行與前六列構成的分塊矩陣，

根據上述分析，傳統UKF 算法中的計算式(6)式、(9)式和(10)式可分別由(8)式、(11)式和(12)式代替，簡化了矩陣運算維數，從而大大降低了計算的復雜度。由此可以得到改進后的SUKF 算法基本計算流程如圖1所示，其中n 為增廣后的系統狀態向量維數，λ =α2(n +k)-n，α 決定采樣點距均值的遠近程度，通常被賦一個較小的正值，本文取α2=0.002，k≥0 保證方差陣的半正定性，本文取0，β 用于包含狀態量分布的高階成分信息，本文取2.

圖1 SUKF 算法計算流程Fig.1 Calculation procedure of simplified unscented Kalman filter algorithm

2 仿真實驗與分析

為有效驗證本文算法的性能，在MATLAB 2009Ra 環境下，對分別采用UKF、SUKF 和EKF 濾波方法的發射慣性系下的SINS/GPS/CNS 組合導航系統性能進行對比分析，同時還將UKF 與SUKF 的計算量進行了對比分析。

2.1 仿真條件

導彈發射初始經度、緯度、高度為:118°、32°、0 m，初始航向角為90°，發射時間為2014年6月1日0 時0 分0 秒，飛行時間為600 s;捷聯解算周期為0.02 s，濾波周期為1 s;仿真中設置捷聯慣性傳感器仿真參數為:陀螺隨機游走驅動噪聲0.2°/h，陀螺白噪聲0.2°/h，加速度計隨機游走驅動噪聲0.000 1 g，加速度計白噪聲0.000 1 g;衛星接收機和星敏感器仿真參數為:衛星導航位置誤差15 m，星光跟蹤儀誤差21″.

2.2 仿真分析

2.2.1 標準彈道飛行航跡

為有效驗證本文算法性能，設計了一條標準導彈飛行軌跡如圖2所示。仿真誤差曲線如下所示，圖3為采用UKF、SUKF 與EKF 算法求解得到的姿態誤差曲線對比圖，圖4為采用UKF、SUKF 與EKF算法求解得到的位置誤差曲線對比圖，圖5為采用UKF、SUKF 與EKF 算法求解得到的速度誤差曲線對比圖。并根據相應的仿真數據，可以獲得各類導航參數的均方誤差RMS 統計結果如表1所示。

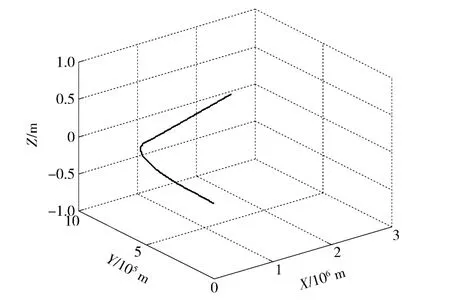
圖2 導彈航跡圖Fig.2 Missile track

圖3 姿態誤差曲線對比圖Fig.3 Attitude error curves

同時估計誤差協方差陣曲線如圖6所示，由于姿態、位置和速度的三軸誤差參數規律大體一致，在此給出滾動角誤差、Y 軸位置誤差和Z 軸速度誤差對應的估計誤差協方差參數。從圖6中可以看出，達到穩態時，采用UKF、SUKF 與EKF 算法求解得到的滾動角估計誤差協方差參數為2.362 rad，2.362 rad，3.774 rad;采用UKF、SUKF 與EKF 算法求解得到的Y 軸位置估計誤差協方差參數為3.038 m，3.038 m，4.166 m;采用UKF、SUKF 與EKF 算法求解得到的Z 軸速度估計誤差協方差參數為0.078 m/s，0.078 m/s，0.206 m/s.

從以上誤差曲線對比圖、誤差RMS 統計表以及估計誤差協方差參數可以看出，SUKF 繼承了UKF 精度高這一優點，其濾波精度較EKF 有顯著的提升。

圖4 位置誤差曲線對比圖Fig.4 Position error curves

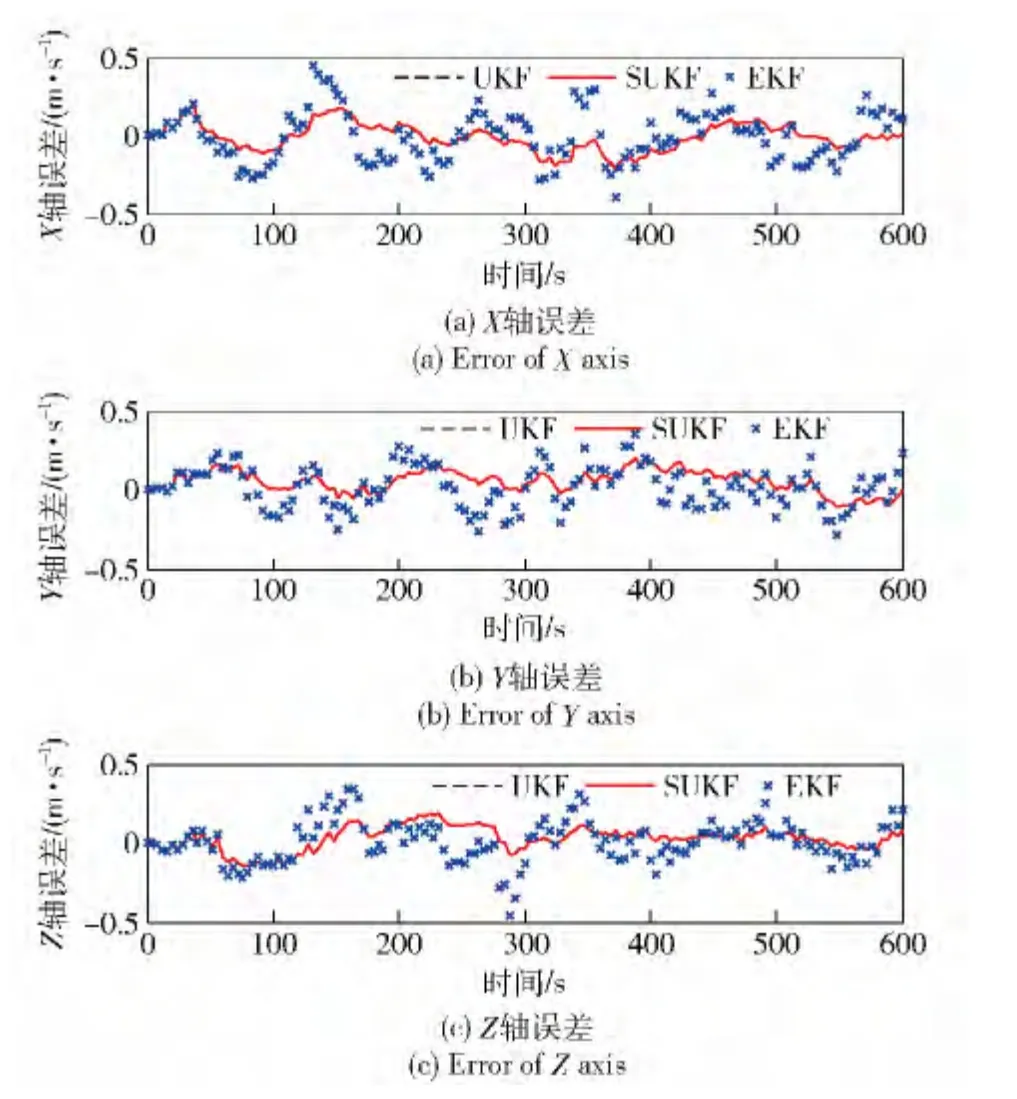
圖5 速度誤差曲線對比圖Fig.5 Velocity error curves

對SUKF 和UKF 算法的計算量進行對比分析，如表2所示。

從表2中還可以看出在同樣的仿真計算條件下，SUKF 算法的計算時間大約比傳統UKF 算法減少了18%，有效降低了計算的復雜度。

表1 組合導航系統UKF、SUKF 與EKF 算法誤差對比表Tab.1 UKF，SUKF and EKF RMS errors of integrated navigation system

表2 算法計算量分析(低動態)Tab.2 Calculated amount (low dynamic range)

圖6 估計誤差協方差參數(低動態)Fig.6 Estimation error covariance matrix parameters(low dynamic range)

2.2.2 高動態飛行航跡

為有效驗證本文算法的性能，還設計了一條高動態環境下導彈飛行軌跡如圖7所示，包含了高速姿態機動等過程。仿真誤差曲線如下所示，圖8為采用UKF、SUKF 與EKF 算法求解得到的姿態誤差曲線對比圖，圖9為采用UKF、SUKF 與EKF 算法求解得到的位置誤差曲線對比圖，圖10 為采用UKF、SUKF 與EKF 算法求解得到的速度誤差曲線對比圖。并根據相應的仿真數據，可以獲得各類導航參數的均方誤差RMS 統計結果，如表3所示。

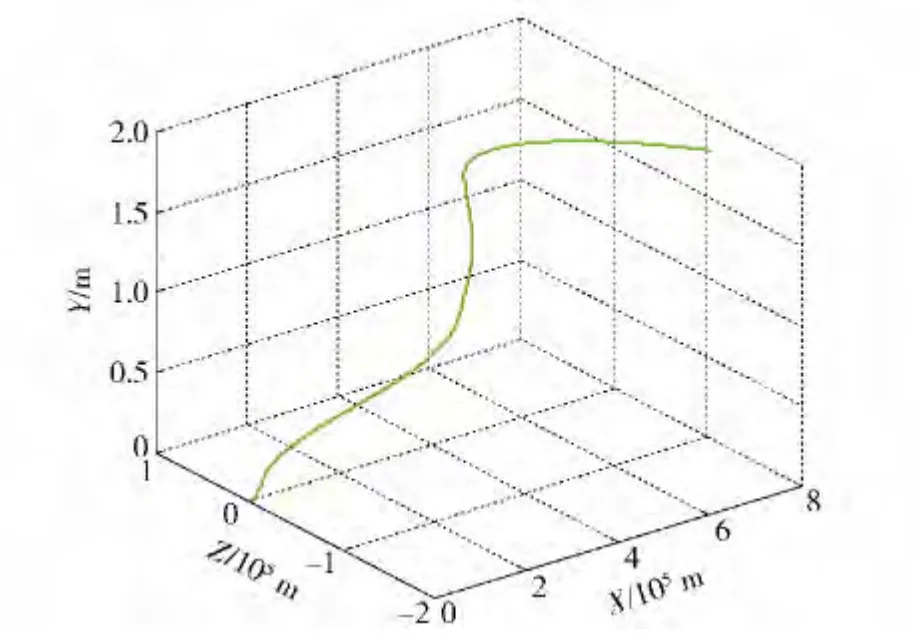
圖7 導彈航跡圖(高動態)Fig.7 Missile track(high dynamic range)

圖8 姿態誤差曲線對比圖(高動態)Fig.8 Attitude error curves(high dynamic range)

估計誤差協方差陣曲線如圖11 所示，從圖11中可以看出，達到穩態時，采用UKF、SUKF 與EKF算法求解得到的滾動角估計誤差協方差參數為2.362 rad，2.362 rad，3.773 rad;采用UKF、SUKF 與EKF 算法求解得到的Y 軸位置估計誤差協方差參數為3.028 m，3.028 m，4.158 m;采用UKF、SUKF 與EKF 算法求解得到的Z 軸速度估計誤差協方差參數為0.079 m/s，0.079 m/s，0.206 m/s.

表3 組合導航系統UKF、SUKF 與EKF 算法誤差對比表(高動態)Tab.3 UKF，SUKF and EKF RMS errors of integrated navigation system

圖9 位置誤差曲線對比圖(高動態)Fig.9 Position error curves(high dynamic range)

從以上誤差曲線對比圖、誤差RMS 統計表以及估計誤差協方差參數可以看出，在高動態環境下，SUKF 依然具備UKF 精度高這一優點，其濾波精度較EKF 有顯著的提升。

對SUKF 和UKF 算法的計算量進行對比分析如表4所示。

從表4中還可以看出，在高動態的仿真計算條件下，SUKF 算法的計算時間大約比傳統UKF 算法減少了17.7%，有效降低了計算的復雜度。

圖10 速度誤差曲線對比圖(高動態)Fig.10 Velocity error curves(high dynamic range)

表4 算法計算量分析(高動態)Tab.4 Calculated amount (high dynamic range)

3 結論

彈載等高動態環境下組合導航系統狀態方程具有強非線性，且各狀態相互耦合影響，傳統的EKF算法由于需要對模型進行線性化展開從而影響導航系統精度，而傳統的UKF 算法又因組合導航系統維數過大而存在濾波過程計算復雜和計算量大的不足，不利于工程實現。為此，本文針對發射慣性系下SINS/GPS/CNS 組合導航系統狀態模型非線性而觀測模型線性的特點，設計了一種SUKF 算法對組合導航系統狀態參數直接進行估計，從而簡化了UKF算法計算步驟，降低了計算的復雜度。算法仿真結果表明SUKF 算法具有比EKF 算法更高的導航精度，同時也有效減少了傳統UKF 算法的計算量，從而為解決高動態環境下非線性濾波估計問題提供了一種有效的方法。

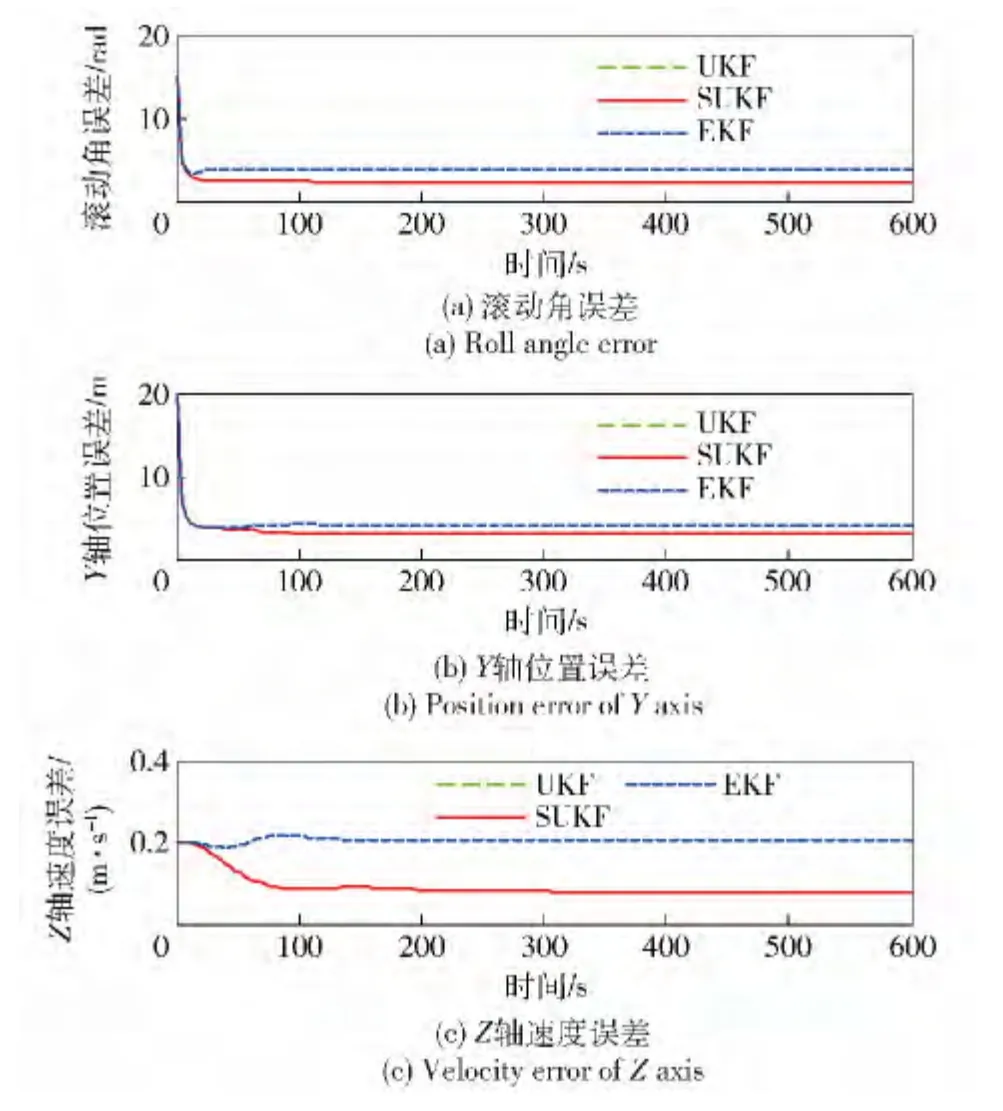
圖11 估計誤差協方差參數(高動態)Fig.11 Estimation error covariance matrix parameters(high dynamic range)

References)

［1］Wang R，Xiong Z，Liu J，et al. SINS/GPS/CNS information fusion system based on improved Huber filter with classified adaptive factors for high-speed UAVs［C］∥Proceeding of the 2012 IEEE/ION Position，Location and Navigation Symposium (PLANS).Myrtle Beach，South Cardina:IEEE，2012:441 -446.

［2］Hu H D，Huang X L.SINS/CNS/GPS integrated navigation algorithm based on UKF［J］. Journal of Systems Engineering and Electronics，2010，21(1):102 -109.

［3］江曉東，謝京穩，郭軍海. 基于UKF 的再入彈道高精度估計方法研究［J］. 航天控制，2011，29(3):28 -32.JIANG Xiao-dong，XIE Jing-wen，GUO Jun-hai.The precision estimation method of reentry target trajectory based on the UKF［J］.Aerospace Control，2011，29(3):28 -32.(in Chinese)

［4］Wang Q T，Xiao D. The research and application of robust UKF algorithm for GPS/SINS integrated system［J］. Journal of Convergence Information Technology，2011，6(6):202 -211.

［5］Majeed M，Kar I N. Aerodynamic parameter estimation using adaptive unscented Kalman filter［J］. Aircraft Engineering and Aerospace Technology，2013，85(4):267 -279.

［6］羅楠，許錄平，張華. 基于UKF 和信息融合的航天器自主導航方法［J］. 中國空間科學技術，2012，32(2):1 -9.LUO Nan，XU Lu-ping，ZHANG Hua. Method of autonomous celestial navigation based on UKF and information fusion［J］. Chinese Space Science and Technology，2012，32(2):1 -9.(in Chinese)

［7］Zhang H T. Unscented Kalman filter and its nonlinear application for tracking a moving target［J］. Optik-International Journal for Light and Electron Optics，2013，13(3):4468 -4471.

［8］Kol?s S，Foss B A，Schei T S. Constrained nonlinear state estimation based on the UKF approach［J］. Computers and Chemical Engineering，2009，33(8):1386 -1401.

［9］周丕森，鮑其蓮. 組合導航系統UKF 濾波算法設計［J］. 上海交通大學學報，2009，43(3):389 -392.ZHOU Pei-sen，BAO Qi-lian. Design of filter in micro-integrated navigation system［J］. Journal of Shanghai Jiaotong University，2009，43(3):389 -392.(in Chinese)

［10］Luo Z，Fang H J. Modified state prediction algorithm based on UKF［J］. Journal of Systems Engineering and Electronics，2013，24(1):135 -140.

［11］Liu J，Ma J. Pulsar/CNS integrated navigation based on federated UKF［J］. Journal of Systems Engineering and Electronics，2010，21(4):675 -681.

［12］Ge Z X，Yang Y M，Zheng H. A new UKF based fault detection method in non-linear systems［J］. International Journal of Plant Engineering and Management，2006，11(3):179 -183.

［13］Rhudy M，Gu Y，Jason V，et al. Evaluation of matrix square root operations for UKF within a UAV GPS/INS sensor fusion application［J］. International Journal of Navigation and Observation，2011:1 -11.

［14］Nowak T，Eidloth A. Dynamic multipath mitigation applying unscented Kalman filters in local positioning systems［J］. International Journal of Microwave and Wireless Technologies，2011，3(3):365 -372.