熱解型絕熱材料燒蝕過程數值仿真

周 源，黃志勇，王 斌

(海軍航空工程學院七系，山東煙臺 264001)

固體火箭發動機中絕熱層的熱防護性能直接影響發動機工作的可靠性和安全性［1］。暴露于高溫高壓燃氣中的絕熱層，主要是通過一種“燒蝕機理”來保護發動機殼體的。絕熱材料在高熱流作用下，由于材料發生化學、物理性質和結構上的變化，生成堅實的碳化層，并進一步產生表面材料燒蝕現象而吸收熱量，從而延緩熱量向殼體內部的傳導。因此，研究絕熱層的傳熱燒蝕規律對確保固體火箭發動機安全工作具有重要意義。

關于熱解型材料的傳熱燒蝕問題已有很多的研究，文獻［2］中和文獻［3］中根據熱解型絕熱材料的特性，對絕熱層燒蝕過程建立了物理結構模型，并提出了數值求解方法。文獻［4］中對于時動邊界上的熱傳導問題的求解提出了人工邊界的方法，文獻［5］中和文獻［6］中采用有限差分法對絕熱層的瞬態傳熱進行計算。

對絕熱層的燒蝕傳熱過程建立了碳化層—熱解面—基體層的物理結構模型，結合絕熱層表面的熱化學燒蝕模型和計算傳熱模型，為絕熱層的燒蝕傳熱研究提供了理論依據。

1 計算模型

1.1 熱化學燒蝕計算模型

在發動機產生的燃氣中，部分氣體組分與絕熱層燒蝕過程中產生的碳化層發生熱化學燒蝕反應。參加燒蝕反應的氣體組分主要是CO2、H2O和H2，將其余不參加燒蝕反應的惰性氣體組分折合成N［7］2。那么，熱化學反應燒蝕率的計算采用以下3個化學反應方程:

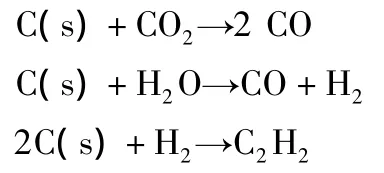
如圖1，在燒蝕表面附面層中，燒蝕反應氣體組分來自于燃氣主流擴散和絕熱層熱解氣體，在燒蝕表面發生反應后被燃氣主流帶走［8，9］。根據質量守恒定理，熱化學燒蝕程序方程組表示如下:

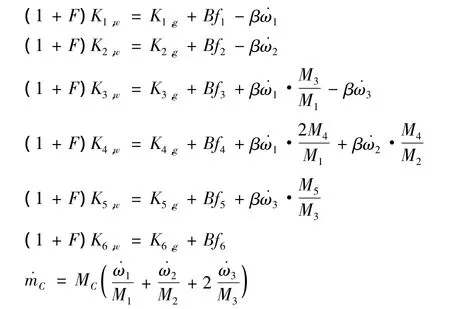
式中:下標1～6分別表示各氣體組分對應的編號;Mi表示化學分子量;˙ωi表示在燒蝕表面上由熱化學反應產生的質量流率;K是組分濃度，fi是熱解氣體中各組分的百分含量;下標w表示燒蝕表面，下標g表示燃氣主流。

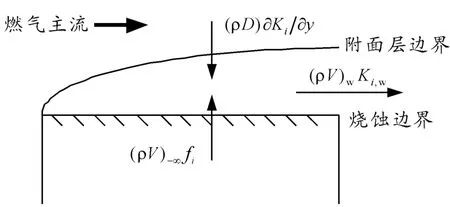
圖1 燒蝕表面質量守恒示意圖

1.2 傳熱計算模型

絕熱層在工作過程中形成碳化層—熱解面—原始材料層的結構，如圖2所示。將絕熱層內部的導熱過程簡化為一維大平板的瞬態導熱［2］，不考慮絕熱材料的熱膨脹及其引起的熱應力，且材料參數隨溫度的變化忽略不計［8］，由此建立傳熱計算模型。

1)碳化層內的瞬態導熱

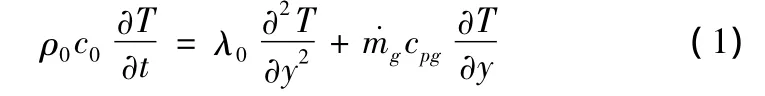
式中:ρ0表示碳化層的密度;c0表示碳化層的比熱;λ0表示碳化層的導熱系數;cpg表示熱解氣體的比熱;˙mg表示熱解氣體的質量流率。

2)熱解面上能量守恒

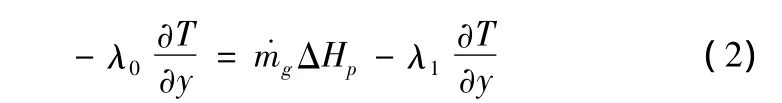
式中:ΔHp表示絕熱材料的熱解潛熱;λ1表示原始材料層的導熱系數;Tp表示絕熱材料的熱解溫度。

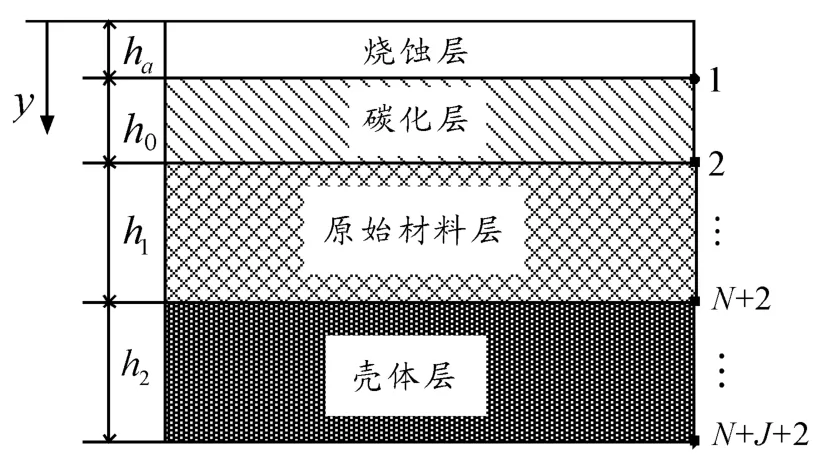
圖2 傳熱計算模型

3)原始材料層內的瞬態導熱

式中:ρ1表示原始材料層的密度;c1表示原始材料層的比熱;λ1表示原始材料層的導熱系數。

4)原始材料層與殼體層之間的界面上能量守恒

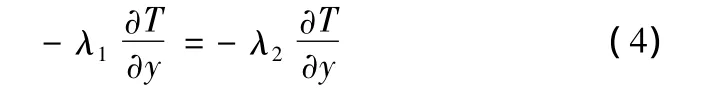
式中，λ2表示殼體層的導熱系數。

5)殼體層內的瞬態導熱

式中:ρ2表示殼體層的密度;c2表示殼體層的比熱;λ2表示殼體層的導熱系數。

6)邊界條件

根據假設，燃氣發生器工作期間與外界是絕熱的。殼體層與外部環境之間的界面上能量守恒

當Tw＜Tp時，絕熱層表面沒有發生碳化，根據邊界條件方程，可得

當Tw≥Tp時，絕熱層表面出現碳化層，根據邊界條件方程，

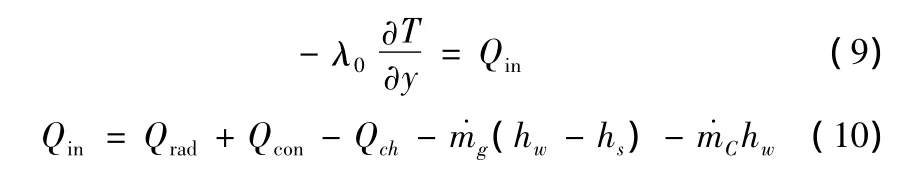
式(8)和式(10)中，Qcon表示對流熱流率;Qrad表示輻射熱流率;hs表示熱解氣體生成熱流率;(+)hw表示壁面處氣體流動帶走的熱流率;燃氣溫度T=3 000 K。圖3為燒蝕界面能量守恒示意圖。

圖3 燒蝕界面能量守恒示意圖

7)初始條件

絕熱層內部初始溫度是常數，取環境溫度。

1.3 數值離散方法

在燒蝕過程中絕熱層的厚度不斷減少，絕熱層內表面不斷移動。對于具有時動邊界的瞬態傳熱問題，采用預測—校正格式［10］進行離散求解。如圖2所示，對每一層結構進行等分離散，則有

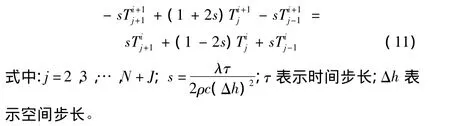
通過與其他數值離散格式對比，該格式具有二階精度且無條件穩定。

2 計算結果與分析

在計算過程中，使用變空間步長的差分方法，節點坐標不斷更新。在每個時間步長上，根據燒蝕速率來確定移動邊界節點的位置，然后重新進行離散，再計算溫度場。

取燒蝕過程中燃氣溫度為3 000 K，燃氣壓力為10 MPa，工作時間為10 s，絕熱層原始厚度為5 mm，時間步長為1 ms。

圖4給出了絕熱層內表面的溫度變化規律。在開始階段，溫度迅速升高，溫度越高，變化速率越小。在達到約2 500 K時，溫度趨于平衡。

圖5給出了絕熱層內表面碳化層的線燒蝕率隨時間變化曲線。在絕熱層表面未形成碳化層的時候，燒蝕率為零。隨著絕熱層內表面溫度的升高，以及燃燒室壓力的增加，根據Arrhenius定律，碳化層燒蝕率逐漸增大。而隨著燃燒室壓力急劇下降，線燒蝕率也急劇下降。

圖6給出了燃氣發生器工作過程中燒蝕線與熱解線的相對位置。在開始階段，絕熱層不發生熱解和碳化。直到絕熱層溫度達到熱解溫度，碳化層厚度迅速增大，并隨著溫度的升高逐漸減緩。從圖6中可以看出，熱解速率明顯比燒蝕速率快很多。

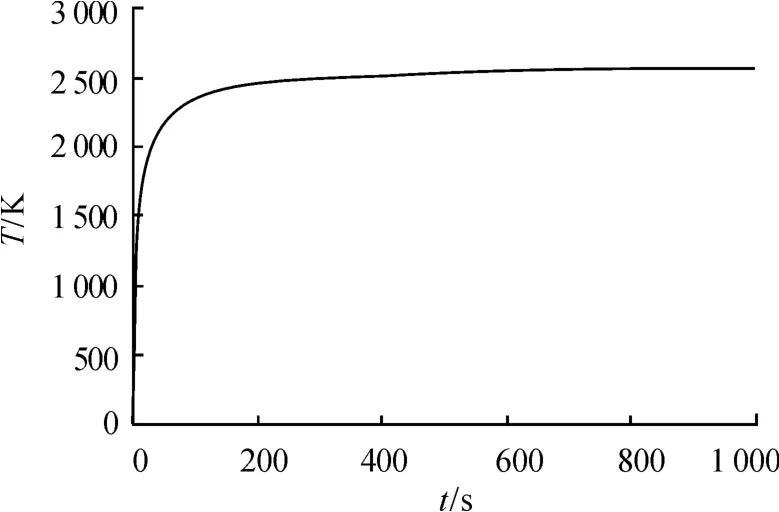
圖4 絕熱層內表面溫度

圖5 碳化層表面線燒蝕率

圖6 燒蝕線和熱解線的相對位置

3 結論

1)本研究建立的熱化學燒蝕模型和傳熱計算模型以及所采用的離散格式和計算方法實現了燒蝕變形與傳熱的雙向耦合。

2)絕熱層的熱解速率比碳化層的燒蝕速率快很多，因此絕熱材料的熱解潛熱對絕熱層的熱防護能力具有極大的影響。

［1］ 鄭亞，陳軍，鞠玉濤，等.固體火箭發動機傳熱學［M］.北京:北京航空航天大學出版社，2006:6－11.

［2］ 徐善瑋，侯曉，張宏安.固體火箭發動機內絕熱層燒蝕質量損失計算［J］.固體火箭技術，2003，26(3):28 －31.

［3］ 張濤，孫冰.三維燒蝕內部熱響應數值計算研究［J］.宇航學報，2012，33(3):298 －304.

［4］ 張雪艷，周愛霞.時動邊界上熱傳導問題的求解方法［J］.廊坊師范學院學報:自然科學版，2010，10(2):9－12.

［5］ 李宛珊，王文洽.二維熱傳導方程的有限差分區域分解算法［J］.山東大學學報:理學版，2011，46(12):1 －5.

［6］ 任麗麗，朱少紅，趙鳳柱.熱傳導方程的C－N格式區域分解方法及其穩定性分析［J］.唐山師范學院院報，2011，33(2):36 －38.

［7］ 張斌，劉宇，王長輝，等.長時間工作固體火箭發動機燃燒室熱防護層燒蝕計算［J］.固體火箭技術，2011，34(2):189－192.

［8］ 楊春杰.固體火箭發動機后效沖量研究［D］.長沙:國防科技大學，2011.

［9］ 何洪慶，嚴紅.EPDM 的燒蝕模型［J］.推進技術，1999，20(4):36－39.

［10］南京大學數學系計算數學專業.偏微分方程數值解法［M］.北京:科學出版社，1979:145－182.

(責任編輯蒲 東)