基于Lagrangian支持向量機的機械手魯棒自適應控制

劉紅平

長沙師范學院 電子信息工程系，長沙 410100

1 引言

多關節(jié)機械手系統是一個多輸入多輸出、高度耦合的復雜非線性系統。如果能夠得到描述機器人動力學的精確數學模型，那么計算力矩控制[1]就能夠有效地實現機器人的軌跡跟蹤控制。然而，計算力矩控制必須事先精確獲得機器人的動力學模型的先驗知識。但在實際中，即使獲得一個較為理想的機器人動力學模型也是很困難的。經典的PD控制不依賴系統模型，然而難以保證系統的穩(wěn)定性和控制精度。在系統模型未知的情況下，為實現機械手的高性能控制，通常在控制律中引入補償項，以消除不確定性因素的影響。傳統的控制方法由于控制精度低（如：PID控制）或缺乏魯棒性（如：計算轉矩控制）等原因，往往難以保證良好的動態(tài)性能。考慮到神經網絡強大的非線性逼近能力，可以補償各種非線性未建模動態(tài)的影響，因此，基于神經網絡的控制方法成為機械手智能控制的重要手段[2-6]。然而，由于神經網絡固有的缺乏泛化性和容易陷入局部極小的缺陷，在一定程度上限制了其應用。支持向量機的提出，有效地解決了這一問題[7-10]。

支持向量機（SVM）是一種基于統計學習理論的學習機[10-14]，通過結構風險最小化準則來提高泛化能力。相對神經網絡來說，SVM具有嚴格的理論基礎，在訓練中不存在陷入局部最優(yōu)和維數災難問題，小樣本學習也具有很強的泛化能力。文獻[15]在標準的支持向量機基礎上提出了一種改進的Lagrangian支持向量機（LSVM），并將其應用到分類問題，實驗結果表明，Lagrangian支持向量機具有更快的計算速度[16-20]。

本文首先將Lagrangian支持向量機推廣應用到回歸問題，學習過程采用梯投影法[21-23]；然后將Lagrangian支持向量機應用于機械手的滑模控制。具體來說，首先通過Lagrangian支持向量機對機械手系統進行非線性補償；然后進一步在線調整參數，并增加一個滑模魯棒控制項來消除逼近誤差對跟蹤性能的影響。最后，通過仿真實現，驗證了以上控制方法的有效性。

2 Lagrangian支持向量機

2.1 LSVM分類

首先考慮標準的支持向量機分類（SVC），標準的二階范數軟間隔SVC形式為：

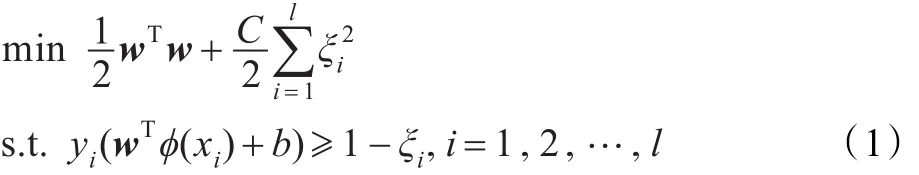
其中，w=(w1，w2，…，wm)T∈Rm，φ(?):Rn→Rm為非線性映射；b為截距，C為正則參數，ξi為松弛變量；((x1，y1)，(x2，y2)，…，(xl，yl))為給定的樣本集，l為樣本個數。其對偶問題為：

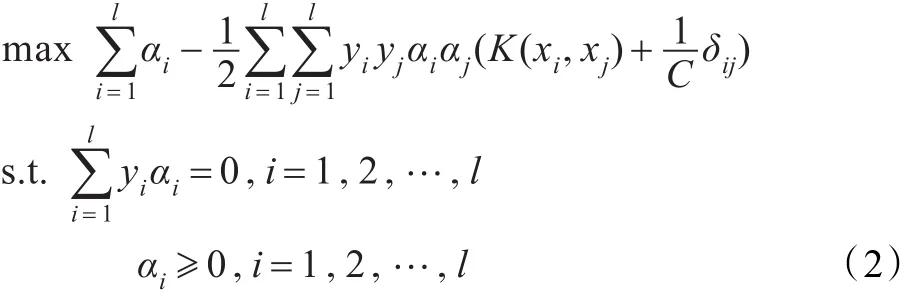
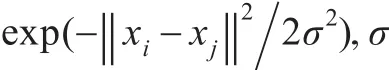
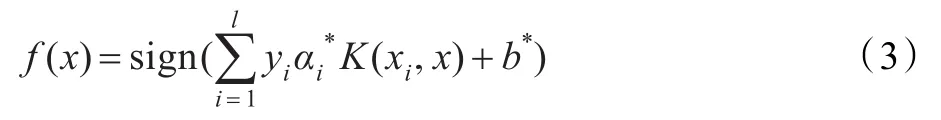
上述SVC的特點是：含有等式約束，且當樣本不可分時的取值并不唯一。Lagrangian支持向量機是上述標準SVC的一種改進，在目標函數b2中增加了項，對應的LSVC形式如下：

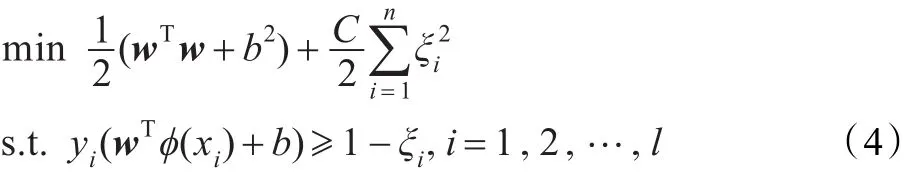
通過引入拉格朗日函數，可將以上問題求解轉化為如下對偶問題：

式（5）相對式（2）來說，沒有了等式約束。因此，使得對應問題的求解相對簡單。設對偶問題（5）的最優(yōu)解為，則唯一的b*滿足以下條件：

這樣得到如下的判別函數：

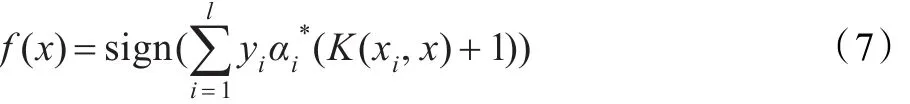
2.2 LSVM回歸

為了能夠將Lagrangian支持向量機（LSVM）應用于函數逼近，將上述LSVM推廣應用到回歸問題。首先定義Huber損失函數：

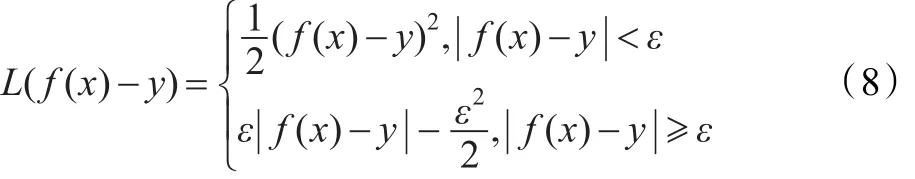
其中ε為不敏感參數。對于具有Huber損失函數的LSVR定義如下：

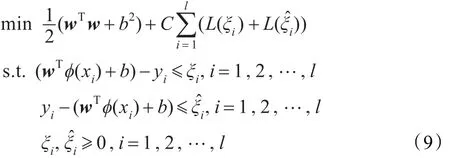
通過引入約束優(yōu)化問題（9）的拉格朗日函數，并利用KKT互補條件，得到其對偶問題為：

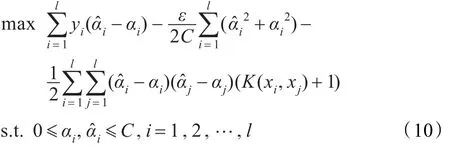
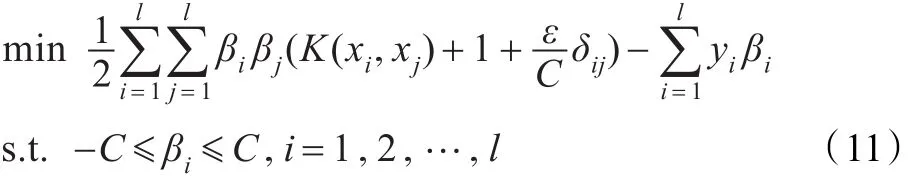
假定通過求解上述二次規(guī)劃問題，得到最優(yōu)解，則相應的回歸函數為：

得到的Lagrangian支持向量機回歸結構如圖1所示，其中xi為支持向量機的輸入，y為輸出；βi可以看作支持向量機網絡的輸出權值。

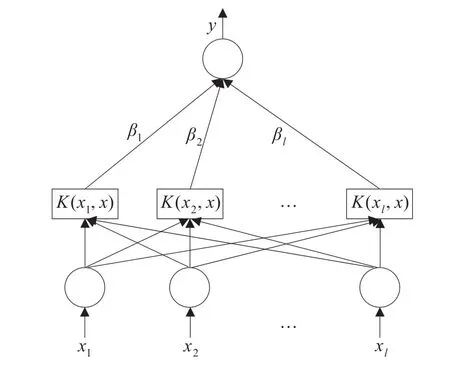
圖1 LSVR結構示意圖

3 LSVR的學習

本部分主要研究如何通過樣本學習獲得LSVR的未知參數βi。為獲得最優(yōu)參數，必須求解含約束的二次規(guī)劃問題（11）。首先將式（11）改寫為如下矩陣形式：

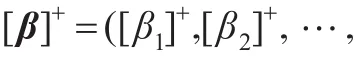
將采用如下梯度投影法求解參數β：

其中，βk為k時刻變量β所在位置，s＞0為學習步長。

下面，將研究參數學習過程的收斂性。對于由式（16）描述的迭代學習過程，有如下定理：

定理1設β*為二次規(guī)劃問題（12）的唯一最優(yōu)解，則當 0＜s＜2/λmax時，迭代式（16）收斂于β*，其中λmax為矩陣A的最大特征值。

證明β*由于為式（12）的唯一最優(yōu)解，則β*必滿足最優(yōu)條件：

將式（16）（17）兩式相減，得：

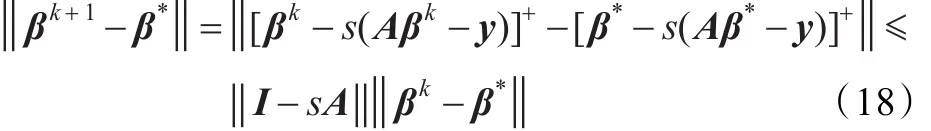
設矩陣A的特征值為λi，i=1，2，…，l，要使得βk收斂于β*，必須有：

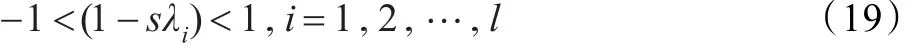
由此即可得 0＜s＜2/λmax時，βk收斂于β*，故得證。

4 機械手控制

在本章中，將把Lagrangian支持向量機回歸（LSVR）應用于機械手系統的控制。對于具有n自由度的機械手，其動力學方程為：

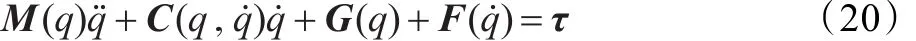
其中，q∈Rn為關節(jié)角位移量，M(q)∈Rn×n為慣性矩陣，C(q，)∈Rn為向心力和哥氏力，G(q)∈Rn為重力矩，F()∈Rn為摩擦力，τ∈Rn為控制力矩。系統（20）具有如下性質：

性質1(q)-2C(q，)為反對稱矩陣，即：

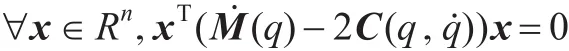
性質2慣性矩陣M(q)為有界的對稱正定矩陣，即存在m1，m2＞0使得：m1I≤M(q)≤m2I

在本文中，系統的控制目標為使得關節(jié)輸出q(t)跟蹤參考輸出qd(t)。對應跟蹤誤差為：

定義誤差函數：

其中，Λ為對稱正定矩陣，則

其中，Kv為對稱正定矩陣。當f未知時，用支持向量機去學習f，用其估計值代替f。然而，由于估計誤差的存在，使得控制器（24）并不能保證閉環(huán)系統的穩(wěn)定性，必須對控制律進行修正。根據支持向量機回歸逼近理論，存在一個最佳逼近，使得：

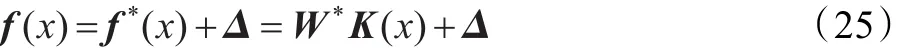
其中Δ為有界的逼近誤差，W*為最佳逼近參數，K(x)為核函數。然而，在實際中通過有限樣本的學習難以精確獲得最佳參數，一般只能獲得參數的近似估計值，即

此時控制力矩為：

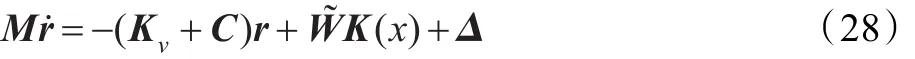
觀察上式，可以將其看作關于參數的含有結構不確定性Δ(t)的模型。對于參數不確定性，設計參數自適應律，對于結構不確定性，可在控制器式（28）的基礎上增加一個魯棒控制器。在設計魯棒控制器時，假設存在常數L＞0，使得有界的逼近誤差實際中，逼近誤差的界也常難以直接得到，因此，先給定L的一個估計值，然后再進行在線調整。

綜合以上分析，實際的控制器由兩部分組成：

且對應的參數自適應律為：

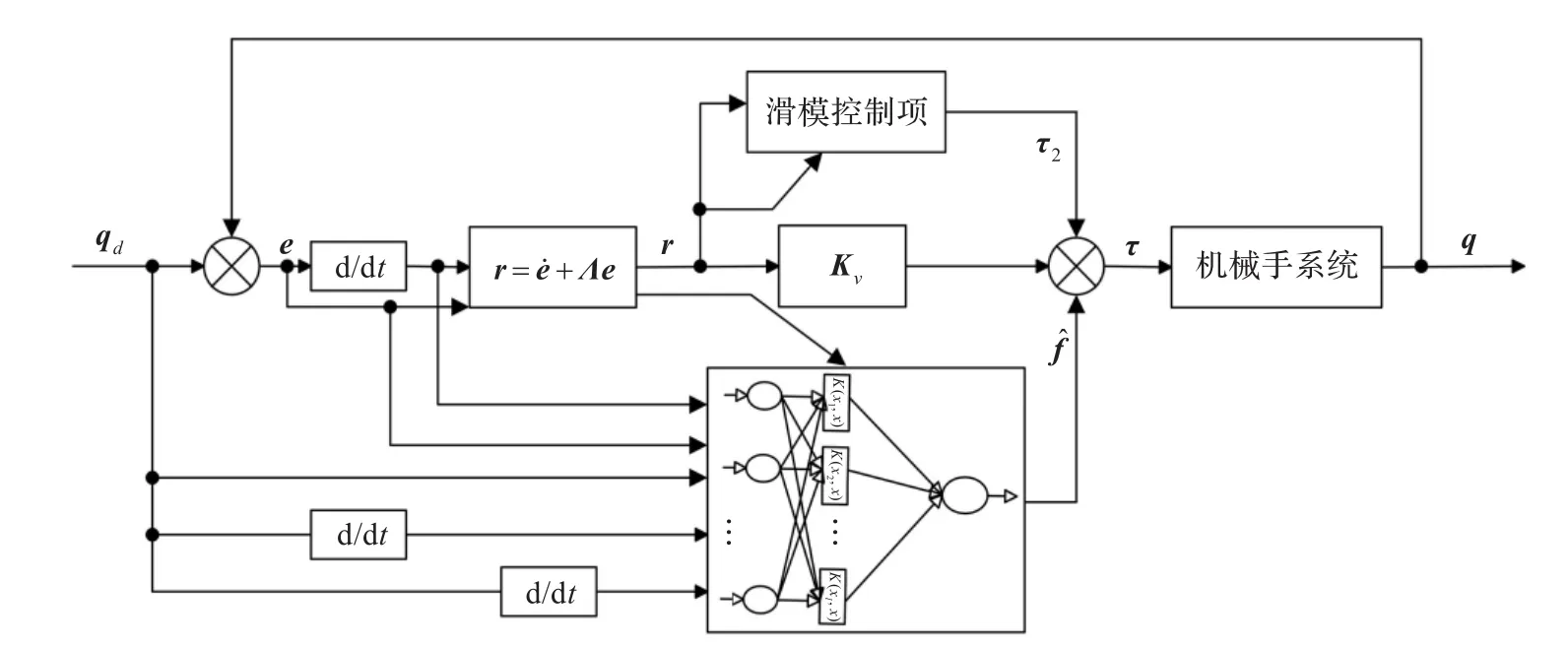
圖2 LSVR控制器框圖

對于此控制器有如下定理：

定理2對于由式（20）描述的機械手系統，若系統控制器由式（29）～（33）確定，則閉環(huán)控制系統漸近穩(wěn)定。

證明定義系統的Lyapunov函數：

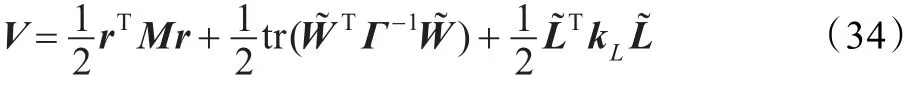
對以上Lyapunov函數求導得：

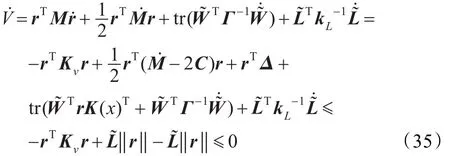
故由Lyapunov穩(wěn)定性理論可得系統的漸近穩(wěn)定性，定理得證。

5 仿真實例

以兩關節(jié)機械手為例，對本文提出的控制方法進行仿真。考慮如圖3所示的二關節(jié)機器手系統，其動力學模型由式（20）描述，其中：

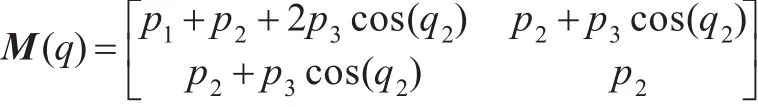
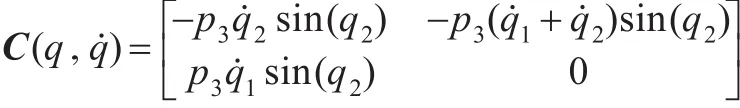
首先利用LSVM對系統進行非線性補償，其中LSVM的正則參數C=5，高斯核函數中的寬度參數σ=2。實施控制時，相應的控制參數取為：Kv=diag(15，10)，Λ=diag(5，5)，kL=0.5，Γ=10。所得到的仿真結果如圖4和圖5所示。另外，為突出跟蹤效果，將本文所提出的方法與經典的PD控制方法進行了對比，其中比例和微分系數的大小選擇與本文提出的控制器中誤差和誤差變化率的系數相同。跟蹤誤差比較效果如圖6和圖7所示。觀察仿真結果可知，本文設計的控制器實現了對參考信號的跟蹤，且比PD控制具有更好的跟蹤性能。這是因為本文提出控制器可以看作在PD控制器的基礎上增加了一個非線性前饋補償器，前饋補償能夠抵消系統非線性和不確定性的影響，有助于提高控制器的跟蹤性能。

圖3 兩關節(jié)機械手模型

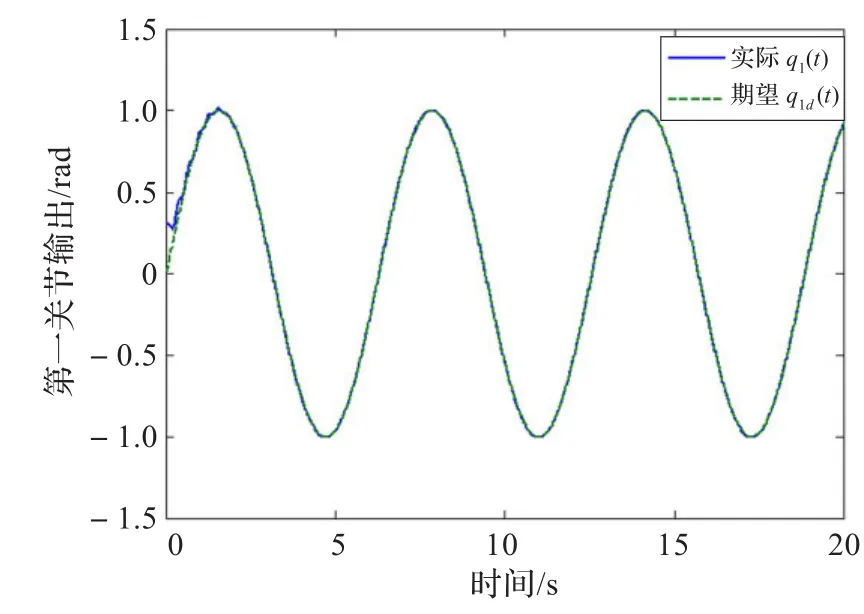
圖4 第一關節(jié)的輸出q1(t)與參考輸出q1d(t)

圖5 第二關節(jié)的輸出q2(t)與參考輸出q2d(t)

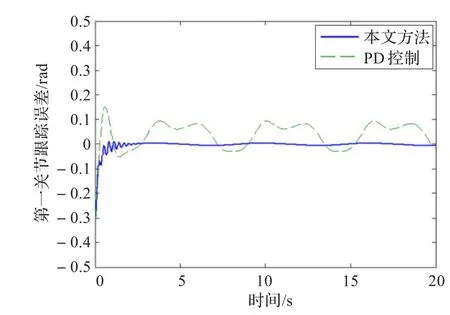
圖6 第一關節(jié)的輸出誤差e1(t)

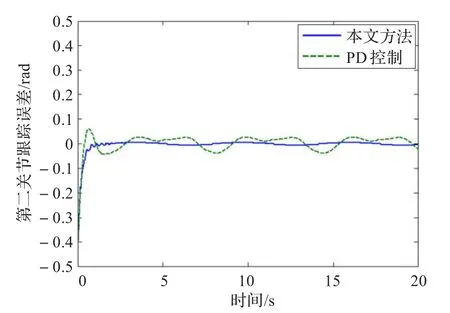
圖7 第二關節(jié)的輸出誤差e2(t)

6 結束語

本文將Lagrangian支持向量機推廣應用到回歸問題，并提出了基于梯度投影法的學習方法，與標準的SVM相比，LSVM具有更快的學習速度。進而采用LSVR補償來實現對機械手的控制，由于補償誤差的存在，因此，在自適應控制器的基礎上增加了一個魯棒控制器，使得控制系統具有了更好的跟蹤性能。對兩關節(jié)機械手的仿真結果表明本文的方法優(yōu)于傳統的PD控制。

[1]Craig J J.Introduction to robotics：mechanics and control[M].3rd ed.New Jersey：Pearson Prentice Hall，2005.

[2]Lewis F L，Liu K，Yesildirek A.Neural net robot controller with guaranteed tracking performance[J].IEEE Trans on Neural Networks，1995，6（3）：703-715.

[3]Lewis F L，Yegildirek A，Liu K.Multilayer neural-net robot controller with guaranteed tracking performance[J].IEEE Trans on Neural Networks，1996，7（2）：388-399.

[4]Byung K Y，Woon C H.Adaptive control of robot manipulator using fuzzy compensator[J].IEEE Trans on Fuzzy Systems，2000，8（2）：186-199.

[5]Meddah D Y，Benallegue A.A stable neuro-adaptive controller for rigid robot manipulators[J].Journal of Intelligent and Robotic Systems，1997，20（2/4）：181-193.

[6]Ge S S，Hang C C.Adaptive neural network control of robot manipulators in task space[J].IEEE Trans on Industrial Electronics，1997，44（6）：746-752.

[7]劉涵，劉丁，任海鵬.基于最小二乘支持向量機的混沌控制[J].物理學報，2005，55（9）：4019-4025.

[8]Sun Zonghai，Sun Youxian，Yang Xuhua，et al.Sequential support vector machine control of nonlinearsystems by state feedback[C]//LNCS 3498：ISNN 2005.Berlin Heidelberg：Springer-Verlag，2005：7-14.

[9]沈曙光，王廣軍，陳紅.最小支持向量機在系統逆動力學辨識與控制中的應用[J].中國電機工程學報，2008，28（5）：85-89.

[10]Mahmoud T A.Adaptive control scheme based on the least squares support vector machine network[J].Int J Appl Math Comput Sci，2011，20（4）：685-696.

[11]Vapnik V.Statistical learning theory[M].New York：John Wiley and Sons，1998.

[12]Cortes C，Vapnik V.Support vector networks[J].Machine Learning，1995，20（3）：273-297.

[13]Cristianini N，Shawe-Taylor J.An introduction to support vector machines[M].Cambridge：Cambridge University Press，2000.

[14]Smola A J，Sch?lkopf B.On a kernel-based method for pattern recognition，regression，approximation，and operator inversion[R].1997.

[15]Mangasarian O L，Musicant D R.Lagrangian support vector machines[J].Journal of Machine Learning Research，2001，1：161-177.

[16]Mangasarian O L，Musicant D R.Successive overrelaxation for support vector machines[J].IEEE Transactions on Neural Networks，1999，10（5）：1032-1037.

[17]Lee Y J，Hsieh W F，Huang C M.ε-SSVR：a smooth support vector machine forε-insensitive regression[J].IEEE Transactions on Knowledge and Date Engineering，2005，17（5）：678-685.

[18]Sheng M，Chen Y，Dai Q.A novel Lagrangian support vector machine and application in the crane gear fault diagnosis system[J].Advances in Mechanical and ElectronicEngineering LectureNotesin ElectricalEngineering，2012，176：369-373.

[19]Hwang J P，Choi B，Hong I W，et al.Multiclass Lagrangian support vector machine[J].Neural Computing and Applications，2013，22（3/4）：703-710.

[20]Shao Y，Chen W，Zhang J，et al.An efficient weighted Lagrangian twin supportvectormachineforimbalanced data classification[J].Pattern Recognition，2014，47（9）：3158-3167.

[21]Xia Youshen，Wang Jun.A one-layer recurrent neural network forsupportvectormachinelearning[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2004，34（2）：1261-1269.

[22]Bertsekas D P，Tsitsiklis J N.Parallel and distributed computation：numericalmethods[M].Englewood Cliffs，NJ：Prentice-Hall，1989：210-219.

[23]Bertsekas D P.Nonlinear programming[M].Massachusetts：Athena Scientific，1999：234-250.