雙平行四邊形碼垛機器人的運動學分析及功能研究

柳賀，萬君，曾輝，劉蕾

(安徽埃夫特智能裝備有限公司蔡鶴皋院士工作站，安徽蕪湖 241009)

0 前言

隨著現代工業的發展，重載搬碼垛運機器人的應用越來越廣泛，結構設計不同，對于機器人運動學算法也不同，但最終目的相同，大多設計成4自由度的串聯機器人，有些針對該4自由度機器人應用D-H法進行運動學求解，計算量相對比較大。

文中以某公司生產的ER180機器人為研究對象，其結構由兩組平行四邊形組成。提出基于幾何法的運動學分析方法，計算量小，便于實時控制，同時對運動算法進行仿真并實際應用，完全滿足要求。

1 機器人模型與坐標系的建立

如圖1所示，主平行四邊形確定末端點位置，上臂的輔助平行四邊形使末端執行器與水平面保持一個固定的姿態。驅動主平行四邊形的電機被對稱安裝在轉座上，其分別標為軸2、軸3，對應關節角度為θ2和θ3;轉座由一個電機驅動，記為軸1，對應關節角度為θ1。前3個關節確定腕部末端點的位置，在手抓處加裝一個電機，轉角記為θ4，用以對所操作工件進行旋轉。

坐標系如圖2所示，其中全局坐標系為O0－x0y0z0，簡記為O系。各個關節為1，2，3，4系，工具坐標系為T系。

圖1 機器人三維模型

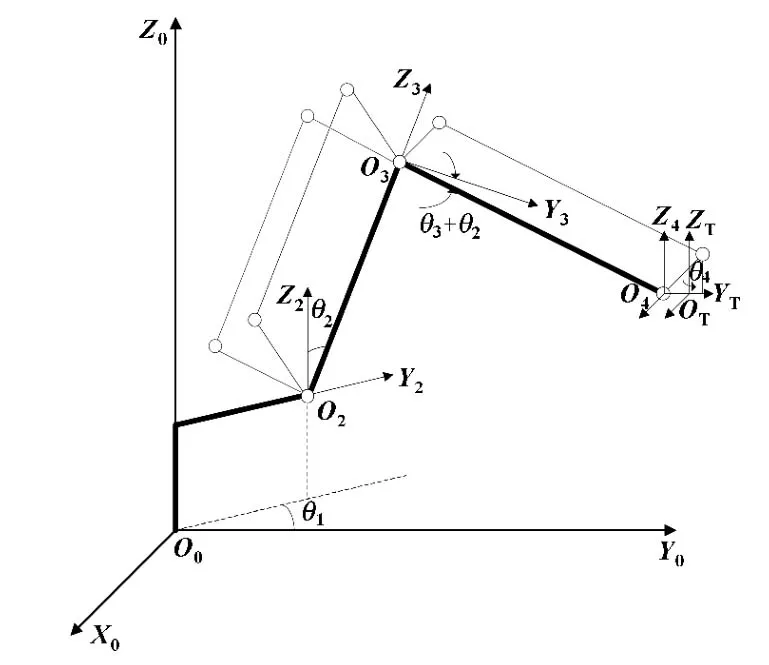
圖2 機器人坐標系

2 機器人運動學正解

已知各個關節的轉角，求得機器人工具端OT的姿態和位置，即為機器人的正解。用坐標變換來描述為從0到T的變換。從圖2可知，從0到1的變換矩陣為1T0。依次類推2T1、3T2、4T3。從而可以得到從 0到4的坐標變換4T0。從0到T的變換為TT0=4T0TT4。即:

其中:TT4=Tz(θ4)+TR(yT，zT)

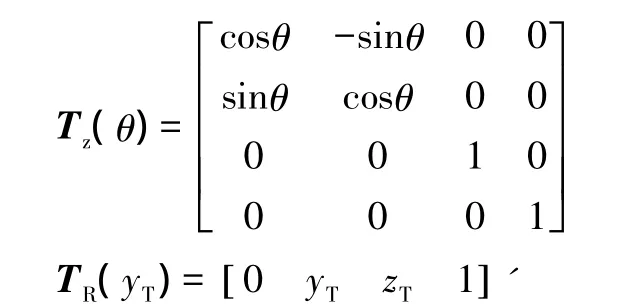
3 碼垛機器人運動學求解

已知末端的位姿，求得各個關節的轉角就是機器人的逆運動學求解。……