定心式彈托對(duì)彈體侵徹混凝土效應(yīng)影響規(guī)律研究

劉堅(jiān)成，黃風(fēng)雷，皮愛(ài)國(guó)，申超

(北京理工大學(xué) 爆炸科學(xué)與技術(shù)國(guó)家重點(diǎn)實(shí)驗(yàn)室，北京100081)

0 引言

平衡炮是一種用于模擬侵徹戰(zhàn)斗部終點(diǎn)彈道及毀傷效應(yīng)的常規(guī)試驗(yàn)加載裝置，通常采用彈托組件發(fā)射次口徑侵徹體，而彈托對(duì)戰(zhàn)斗部侵徹終點(diǎn)效應(yīng)的影響往往被忽略。相比卡瓣式氣動(dòng)分離彈托而言，前后定心式彈托組件可保證侵徹體的膛內(nèi)穩(wěn)定性且在著靶前對(duì)彈體姿態(tài)無(wú)干擾，因此更適用于次口徑彈體高速侵徹試驗(yàn)。早期的脫殼技術(shù)通常采用三瓣式氣動(dòng)分離彈托，為避免托瓣在氣動(dòng)分離時(shí)對(duì)彈飛行姿態(tài)的影響，美國(guó)學(xué)者提出了尾翼穩(wěn)定次口徑氣推彈托脫殼技術(shù)［1］和非包裹卡瓣式彈托技術(shù)［2］。隨著侵徹著速的提高，彈體相對(duì)平衡炮口徑減小，彈托組件的相對(duì)附加質(zhì)量增加，彈托對(duì)侵徹終點(diǎn)效應(yīng)的影響程度逐漸增加。為了獲得足夠精確的侵徹試驗(yàn)數(shù)據(jù)，需要通過(guò)合理設(shè)計(jì)，使彈托對(duì)終點(diǎn)效應(yīng)的影響盡可能降低，與之相關(guān)的科學(xué)問(wèn)題包括:彈托的相對(duì)附加質(zhì)量、彈托組件與彈體連接強(qiáng)度，在不同侵徹著速下對(duì)侵徹終點(diǎn)效應(yīng)影響的量化規(guī)律如何?利用平衡炮進(jìn)行次口徑彈體侵徹試驗(yàn)時(shí)如何確定彈靶設(shè)計(jì)準(zhǔn)則?

為定量研究高速侵徹試驗(yàn)時(shí)定心彈托對(duì)戰(zhàn)斗部侵徹終點(diǎn)效應(yīng)的影響規(guī)律，本文在文獻(xiàn)［3］Forrestal侵徹模型基礎(chǔ)上，建立了帶有前后定心式彈托的剛性彈體侵徹模型，分析了彈托相對(duì)附加質(zhì)量、彈托組件與彈體連接強(qiáng)度、彈體侵徹著速等對(duì)彈體侵徹終點(diǎn)效應(yīng)的影響規(guī)律，研究結(jié)果可為次口徑發(fā)射條件下彈托設(shè)計(jì)及侵徹終點(diǎn)效應(yīng)的評(píng)價(jià)提供參考。

1 帶前后定心式彈托的彈體侵徹模型

1.1 侵徹阻力表達(dá)形式

圖1 為帶有前后定心式彈托的彈體結(jié)構(gòu)示意圖，其中彈體全長(zhǎng)為L(zhǎng)，前定心彈托距彈體頭部尖端為lf，后定心彈托距前定心彈托距離為lb，彈體直徑d，彈托直徑D. 前彈托質(zhì)量mf，后彈托質(zhì)量mb，戰(zhàn)斗部自身質(zhì)量m，前彈托寬度bf，后彈托寬度bb.

圖1 前后定心彈托彈體結(jié)構(gòu)示意圖Fig.1 Projectile structure with forward and back centering sabots

對(duì)于侵徹模型的計(jì)算，F(xiàn)orrestal 等［3］在空腔膨脹理論的基礎(chǔ)上將彈體侵徹混凝土靶的過(guò)程分為開(kāi)坑區(qū)和隧道區(qū)兩部分，并分別給出了阻力表達(dá)式:

圖2 中給出了彈體脫殼侵徹的示意圖，侵徹過(guò)程分為5 個(gè)階段，每階段的受力及過(guò)載均有不同的求解方式，需單獨(dú)分析:圖2(b)侵徹開(kāi)坑階段由彈體與彈托附加質(zhì)量聯(lián)合作用，選取(1)式描述;圖2(c)中前彈托分離時(shí)由彈體與后彈托附加質(zhì)量共同作用，假設(shè)彈托與隧道區(qū)接觸時(shí)發(fā)生前彈托分離現(xiàn)象，脫殼作用力的大小與前彈托連接強(qiáng)度σs有關(guān)。因彈托與彈體之間是由螺紋連接，可由螺紋配合結(jié)構(gòu)給出螺紋的剪切面積［4］，前彈托與彈體承受剪力的螺紋面積近似為則螺紋的抗剪強(qiáng)度為Ff=σsAsf;圖2(d)中彈體與后彈托附加質(zhì)量聯(lián)合侵徹，參考脫前殼的參數(shù)，后彈托螺紋面積阻力Fb=σsAsb;圖2(f)后彈托脫掉后，彈體將在隧道區(qū)保持穩(wěn)定的侵徹過(guò)程，應(yīng)用(2)式即可求解該區(qū)域的受力情況。至此，給出帶彈托侵徹模型中5 個(gè)過(guò)程的阻力及過(guò)載表達(dá)式如(3)式和(4)式所示，可計(jì)算帶彈托彈體侵徹的運(yùn)動(dòng)過(guò)程。

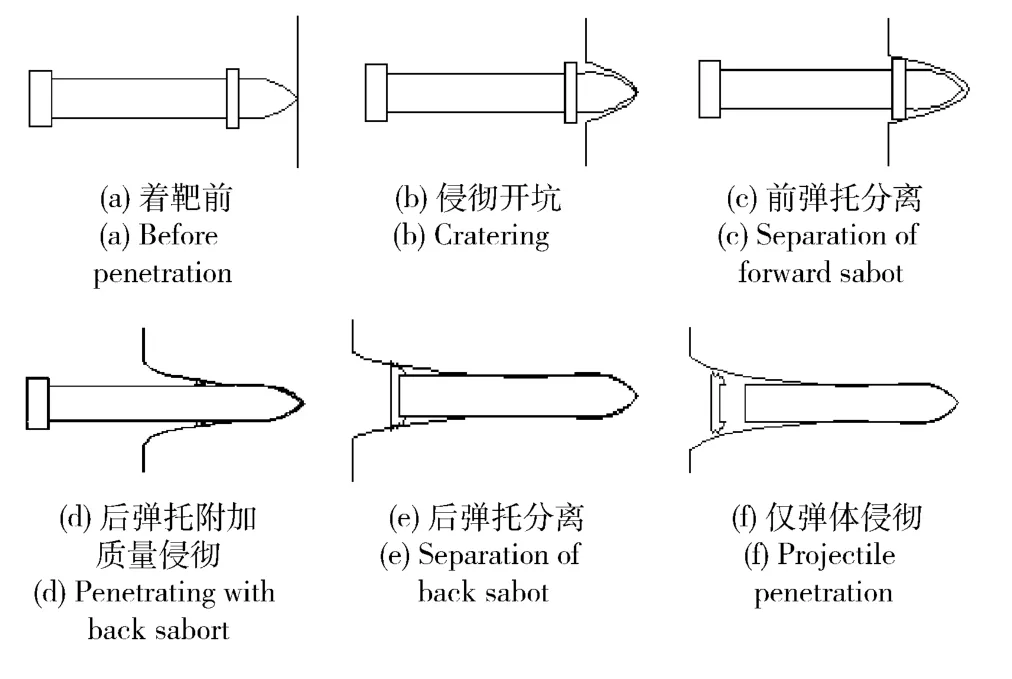
圖2 彈體脫殼侵徹過(guò)程示意圖Fig.2 Schematic diagram of projectile Discarding sabot process

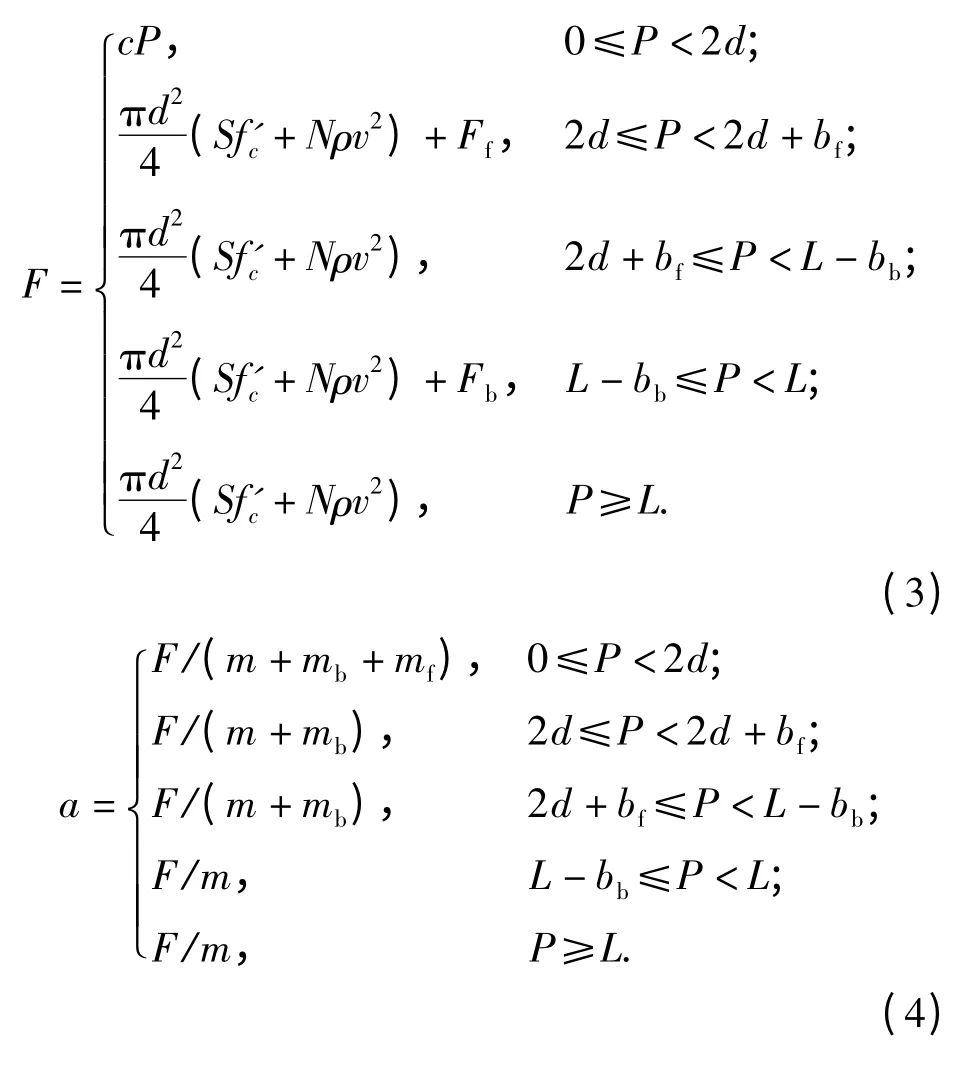
1.2 侵徹深度解析表達(dá)式

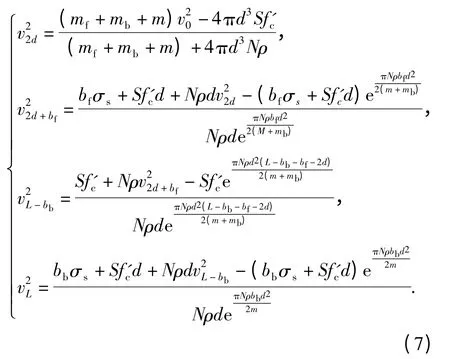
根據(jù)Forrestal 等［3］給出的侵徹深度求解方法及最終的侵徹深度公式為

通過(guò)改變求解過(guò)程中的積分上下限及阻力函數(shù)形式可分別求得幾種不同區(qū)域的侵徹深度表達(dá)式如(6)式所示，其中v2d、v2d+bf、vL-bb、vL分別為侵徹深度2d、2d+ bf、L - bb、L 時(shí)彈體的速度，表達(dá)形式見(jiàn)(7)式。

假設(shè)彈體的基本參數(shù)m =100 kg，kb=1.25kf，d=0.08 m，bf=bb=0.03 m當(dāng)k 取不同值時(shí)，為簡(jiǎn)化vL的表達(dá)式，對(duì)侵徹初速v0與vL的關(guān)系進(jìn)行二次擬合簡(jiǎn)化處理，如圖3 所示。

圖3 不同k 取值時(shí)v0和vL的曲線關(guān)系Fig.3 Relation between v0 and vL for different k

由圖3 可知，3 條曲線的表達(dá)式分別為vL=x +yv0+，求解k 與x、y、z 的線性關(guān)系如圖4 所示。得到

則vL的表達(dá)式可寫(xiě)為

通過(guò)vL與v0的關(guān)系，將(9)式代入(6)式可直接寫(xiě)出P≥L 時(shí)含定心彈托的彈體侵徹深度表達(dá)式。

1.3 侵徹模型試驗(yàn)驗(yàn)證

為驗(yàn)證侵徹模型的正確性，開(kāi)展帶前后定心式彈托侵徹試驗(yàn)，試驗(yàn)中彈靶參數(shù)如表1 所示。彈體初速812 m/s，侵徹深度2.34 m. 利用1.1 節(jié)中的阻力模型對(duì)該工況下的彈體侵徹過(guò)程進(jìn)行迭代計(jì)算，得出彈體的侵徹深度時(shí)程曲線如圖5 所示，圖中兩點(diǎn)分別代表試驗(yàn)結(jié)果和利用(9)式方法擬合計(jì)算得到的侵徹深度。侵徹深度與理論預(yù)估及擬合公式計(jì)算結(jié)果基本一致，且大于無(wú)彈托彈體的侵徹深度。

表1 彈體與靶板的物理參數(shù)Tab.1 The physical parameters of projectile and target

2 脫殼侵徹性能及殼體參數(shù)影響關(guān)系

2.1 彈托相對(duì)附加質(zhì)量對(duì)侵徹深度影響規(guī)律研究

圖4 k 與x、y、z 的線性擬合關(guān)系Fig.4 Linear fitting of k and x、y、z

對(duì)于相對(duì)附加質(zhì)量系數(shù)k =kf+kb的研究，主要從總附加質(zhì)量系數(shù)k 對(duì)侵徹深度的影響及kf和kb分別對(duì)侵徹深度的影響兩方面進(jìn)行研究。

以初速850 m/s 為例，給出不同k 值與無(wú)量綱侵徹深度的關(guān)系如圖6 所示。由圖中可知，帶前后定心式彈托的彈體侵徹深度隨彈托質(zhì)量比k 值的增加而增加，且總k 值相同時(shí)kb在k 中所占的比重越大，對(duì)侵徹深度的增益效果越明顯，即對(duì)侵徹終點(diǎn)效應(yīng)的干擾越大。圖7 給出了初速850 m/s 在不同k取值時(shí)的侵徹過(guò)載時(shí)程曲線，可見(jiàn)圖中有兩個(gè)波峰A、B，此兩個(gè)波峰為脫前殼與脫后殼時(shí)產(chǎn)生的過(guò)載震蕩，因脫殼前后質(zhì)量發(fā)生變化且脫殼過(guò)程受到阻力作用。

圖5 試驗(yàn)結(jié)果與理論預(yù)估的侵徹深度時(shí)程曲線Fig.5 Experimental and theoretical penetration depths vs. time

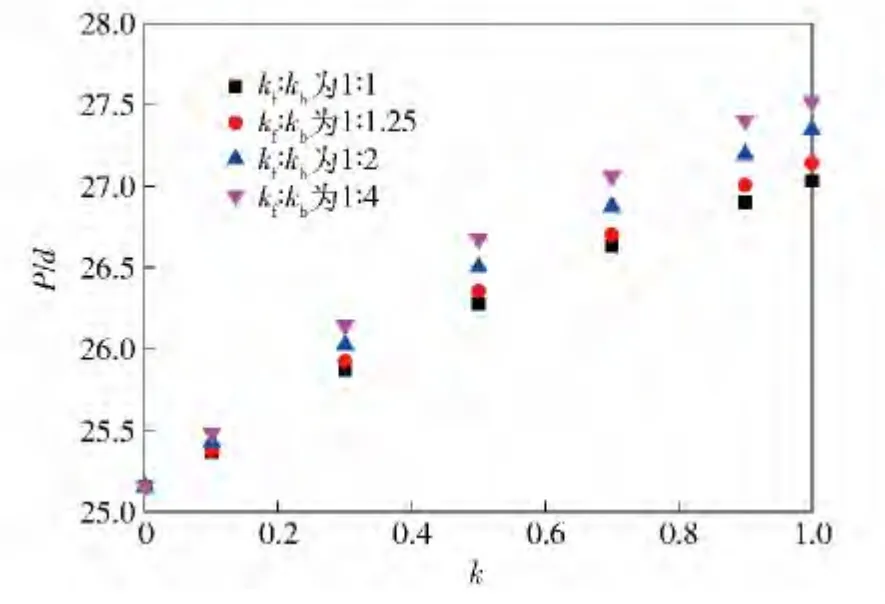
圖6 初速850 m/s 時(shí)k 值與無(wú)量綱侵徹深度的關(guān)系Fig.6 Relation between k and dimensionless penetration depth at 850 m/s

圖7 初速850 m/s 在不同k 值下的過(guò)載時(shí)程曲線Fig.7 Decelerations with different k at 850 m/s

2.2 彈托組件與彈體連接強(qiáng)度對(duì)侵徹深度的影響規(guī)律

彈托組件與彈體連接強(qiáng)度主要與二者固連寬度相關(guān)。彈托寬度較大(彈托與彈體連接強(qiáng)度較大)時(shí)，侵徹深度逐漸減小;對(duì)于總寬度相同但前后彈托寬度不同時(shí)，后彈托越寬，對(duì)侵徹深度減小越明顯。圖8 中給出了彈托寬度與侵徹深度的關(guān)系，圖9 給出了3 種固連條件下的侵徹過(guò)載曲線。當(dāng)彈托寬度越大時(shí)對(duì)應(yīng)于彈托與彈體的連接強(qiáng)度越大，脫殼時(shí)產(chǎn)生的過(guò)載幅值增加，持續(xù)時(shí)間增長(zhǎng)，此為侵徹深度減小的主要原因。

圖8 初速850 m/s 時(shí)不同彈托寬度與無(wú)量綱侵徹深度的關(guān)系Fig.8 Dimensionless penetration depths with different s abot widths at 850 m/s

圖9 初速850 m/s 在不同λ 值下的過(guò)載曲線Fig.9 Decelerations with different sabot widths at 850 m/s

2.3 不同侵徹著速條件下彈托對(duì)侵徹深度的影響規(guī)律

在研究不同侵徹初速v0對(duì)侵徹終點(diǎn)效應(yīng)影響時(shí)，給出了不同k 值不同初速v0下的侵徹深度增量百分比，如圖10 所示。假設(shè)相對(duì)影響量在±5%范圍內(nèi)可接受，可通過(guò)合理設(shè)計(jì)不同附加質(zhì)量k 值、改變彈托與彈體固連強(qiáng)度來(lái)實(shí)現(xiàn)。隨著侵徹速度增加，彈托的連接強(qiáng)度對(duì)侵徹深度的影響越來(lái)越小。因彈托連接強(qiáng)度對(duì)侵徹深度起到減小作用，而彈托質(zhì)量對(duì)侵徹深度起到增益作用，故合理分配二者關(guān)系可使彈托對(duì)侵徹的影響降為最低，如圖11 中λ =0.2，kf∶kb為1∶1.25，k =0.5 時(shí)在馬赫數(shù)為1.5 ～4的著速時(shí)彈靶附加質(zhì)量對(duì)侵徹深度的影響均小于5%.

圖10 不同k 值在不同初速v0下的侵徹深度增量百分比Fig.10 The incremental percentage of penetration depth with different k at different impact velocities

圖11 不同λ 值在不同初速v0下的侵徹深度增量百分比Fig.11 The incremental percentage of penetration depths with different λ at different impact velocities

2.4 含彈托組件彈體侵徹能力數(shù)值模擬

為研究正侵徹條件下彈托對(duì)于高速?gòu)楏w侵徹混凝土靶結(jié)果的影響規(guī)律，利用LS-DYNA 有限元軟件分別開(kāi)展對(duì)帶彈托彈體與不帶彈托彈體在初速的馬赫數(shù)為1 ～4 時(shí)侵徹半無(wú)限厚混凝土靶的數(shù)值模擬研究，其中計(jì)算模型參數(shù)選用1.3 節(jié)中試驗(yàn)所得數(shù)據(jù)進(jìn)行標(biāo)定，模擬選取彈體及混凝土與試驗(yàn)相同，并針對(duì)該彈靶條件下的不同侵徹速度，對(duì)其帶彈托與不帶彈托及彈托的不同連接強(qiáng)度下3 種情況進(jìn)行模擬，與試驗(yàn)及理論計(jì)算結(jié)果進(jìn)行對(duì)比。

采用1∶1等比例建模，因試驗(yàn)彈體采用高強(qiáng)鋼，侵徹過(guò)程中侵蝕量極小，可視為理想剛體，故彈體選用剛體本構(gòu)模型，前后定心式彈托采用塑性動(dòng)態(tài)硬化本構(gòu)模型。考慮彈體侵徹過(guò)程中混凝土靶的破碎、成坑和崩落現(xiàn)象，混凝土靶采用自定義的TCK材料模型。帶彈托彈體正侵徹混凝土靶的過(guò)程如圖12 所示。由圖12 可知，彈體脫前殼及后殼的位置均接近開(kāi)坑區(qū)與隧道區(qū)銜接處，驗(yàn)證了理論模型中脫殼位置假設(shè)的合理性。

圖12 侵徹脫殼過(guò)程圖Fig.12 Penetration process

圖13 侵徹深度隨初速的變化曲線(k=0.144)Fig.13 Relationship between penetration depth and initial velocity(k=0.144)

圖13中給出了24 種計(jì)算工況與理論預(yù)估的侵徹初速與侵徹深度曲線，可知隨侵徹初速的提高，彈托附加質(zhì)量對(duì)侵徹深度增加量影響逐漸增大。而對(duì)于不同彈托連接強(qiáng)度，當(dāng)連接強(qiáng)度增大時(shí)，低速侵徹?zé)o法完成脫后殼的過(guò)程，當(dāng)速度到達(dá)500 m/s 左右時(shí)才可脫掉后殼，此處侵徹深度存在拐點(diǎn)。隨侵徹速度的提高，不同彈托連接強(qiáng)度的彈托對(duì)侵徹深度的影響減弱，侵徹深度相近。當(dāng)初速達(dá)到1 000 m/s時(shí)，λ=0.42 的彈體侵徹深度已經(jīng)超過(guò)無(wú)彈托的彈體。對(duì)比數(shù)值模擬、試驗(yàn)結(jié)果和理論預(yù)估曲線，三者吻合較好，說(shuō)明文中理論模型的正確性，同時(shí)證明了文中數(shù)值模擬的可信性，進(jìn)一步驗(yàn)證了前文所得結(jié)果。

3 結(jié)論

利用侵徹阻力分段計(jì)算公式，對(duì)帶前后定心式彈托的侵徹脫殼過(guò)程進(jìn)行求解，得出了脫殼侵徹深度的解析表達(dá)式，并對(duì)計(jì)算參數(shù)進(jìn)行了擬合，建立了適用于彈托與彈體質(zhì)量比k 在0.1 ～1，初速馬赫數(shù)1 ～4 范圍內(nèi)的彈體侵徹深度計(jì)算求解方法，得到以下主要結(jié)論:

1)彈托附加質(zhì)量越大，對(duì)侵徹深度增益越明顯，對(duì)于試驗(yàn)彈體在不同彈托附加質(zhì)量侵徹時(shí)誤差可達(dá)9%，過(guò)載曲線中脫后殼時(shí)峰值基本不變，脫前殼的峰值逐漸減小;后彈托質(zhì)量越大時(shí)，對(duì)侵徹深度影響越明顯，誤差約為2%.

2)彈托組件與彈體連接強(qiáng)度越強(qiáng)，使侵徹深度減小，脫殼時(shí)過(guò)載峰值越大，持續(xù)時(shí)間越長(zhǎng)。對(duì)于試驗(yàn)彈體，極限情況下彈托與彈體完全連接與不帶彈托情況對(duì)比，侵徹深度誤差可達(dá)58%.

3)隨侵徹著速的增加，同樣設(shè)計(jì)下的彈托附加質(zhì)量影響變小，如100 kg 戰(zhàn)斗部在馬赫數(shù)為3 的著速的侵徹試驗(yàn)中，彈托附加質(zhì)量為15%時(shí)對(duì)終點(diǎn)效應(yīng)影響不超過(guò)3%.

4)為保證試驗(yàn)精度，在中低速侵徹時(shí)(300 ～750 m/s)，應(yīng)盡量減小彈托附加質(zhì)量與彈托連接強(qiáng)度，當(dāng)k=0.144 且λ=0.08 時(shí)可將彈托影響控制在5%以內(nèi);高速侵徹時(shí)(750 ～1 400 m/s)，k =0.144且λ=0.42 時(shí)可將彈托影響控制在5%以內(nèi)。針對(duì)不同著速等彈靶影響條件，可合理設(shè)計(jì)彈托附加質(zhì)量、彈托與彈體連接強(qiáng)度，將影響偏差控制在可接受范圍內(nèi)。

References)

［1］Luther H W. Fin stabilized，subcaliber propelling cage sobot projectile:US，4920889［P］. 1990-05-01.

［2］Eches N，Bachelier J，Leblond J，et al. Sabot for fin-stabilized ammunition:US，6805058B2［P］. 2004-10-19.

［3］Forrestal M J，Altman B S，Cargile J D，et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets［J］. International Journal of Impact Engineering，1994，15(4):395 -405.

［4］機(jī)械設(shè)計(jì)手冊(cè)編委會(huì). 機(jī)械設(shè)計(jì)手冊(cè):第2 卷［M］. 北京:機(jī)械工業(yè)出版社，2008:9 -97.Editorial Board of Machine Design Manual. Machine design manual:Vol 2［M］. Beijing:China Machine Press，2008:9 -97. (in Chinese)