雙電機耦合驅(qū)動履帶車輛自適應(yīng)滑模轉(zhuǎn)向控制

蓋江濤，黃守道，周廣明，劉翼，馬田

(1.湖南大學(xué) 電氣與信息工程學(xué)院，湖南 長沙410082;2.中國北方車輛研究所 車輛傳動重點實驗室，北京100072)

0 引言

采用電傳動可以使履帶車輛實現(xiàn)能源的多元化利用，比機械或液力機械綜合傳動具有諸多無可比擬的優(yōu)點，如無級變速、效率高、易于布置、更適合于采用現(xiàn)代控制技術(shù)等優(yōu)點［1］。轉(zhuǎn)向控制技術(shù)極大地影響著車輛的機動性能。為了解決經(jīng)典的雙電機獨立驅(qū)動無法實現(xiàn)履帶車輛轉(zhuǎn)向再生功率機械循環(huán)的問題［2］，文獻(xiàn)［3］提出了一種雙電機耦合驅(qū)動技術(shù)方案，是典型的雙輸入雙輸出系統(tǒng)。

目前的電傳動履帶車輛轉(zhuǎn)向控制策略，一般都沒有考慮履帶車輛的轉(zhuǎn)向動力學(xué)過程對電機的驅(qū)動轉(zhuǎn)矩做反饋性自適應(yīng)調(diào)節(jié)，導(dǎo)致較難實現(xiàn)任意轉(zhuǎn)向目標(biāo)的跟蹤控制。文獻(xiàn)［4］基于神經(jīng)網(wǎng)絡(luò)PID 控制方法，實現(xiàn)了一定車速范圍內(nèi)的轉(zhuǎn)向目標(biāo)跟蹤控制，但由于其神經(jīng)網(wǎng)絡(luò)主要針對電機阻力矩進(jìn)行訓(xùn)練，較難體現(xiàn)履帶車輛高速轉(zhuǎn)向時的慣性力負(fù)載，只實現(xiàn)了低速轉(zhuǎn)向具有較好的操控性能。文獻(xiàn)［5］基于模型參考自適應(yīng)控制方法，實現(xiàn)了差速轉(zhuǎn)向控制，但控制效果較為依賴參考模型，穩(wěn)定性較差。雙電機耦合驅(qū)動雖然機械特性很好，但是雙電機的耦合作用卻使得轉(zhuǎn)向控制更加復(fù)雜。如何針對履帶車輛轉(zhuǎn)向動力學(xué)固有特性來設(shè)計魯棒性好的雙電機耦合驅(qū)動控制算法，是履帶車輛轉(zhuǎn)向控制的難題。

本文在轉(zhuǎn)向動力學(xué)模型存在不確定參量，以及兩電機驅(qū)動轉(zhuǎn)矩高度耦合的前提下，通過系統(tǒng)動力學(xué)解耦結(jié)合滑模變結(jié)構(gòu)控制，建立了一種魯棒性較好的轉(zhuǎn)向控制算法，實現(xiàn)了對履帶車輛轉(zhuǎn)向的快速穩(wěn)定控制。搭建了“駕駛員—控制器”在環(huán)的雙電機驅(qū)動耦合履帶車輛實時仿真系統(tǒng)，進(jìn)行了不同工況的控制算法的仿真驗證。

1 系統(tǒng)描述

1.1 履帶車輛轉(zhuǎn)向動力學(xué)模型

建立履帶車輛轉(zhuǎn)向動力學(xué)分析圖(見圖1)，O 點在固定坐標(biāo)系中的坐標(biāo)(X，Y，Z)用于確定車輛中心的運動軌跡，C 點為固定坐標(biāo)系的原點，θ 用于確定車體相對Y 軸的逆時針方向角，即車體繞Z 軸的轉(zhuǎn)角，Z 軸方向與X、Y 軸由右手定則確定。x、y、θ作為隨動坐標(biāo)，它們的導(dǎo)數(shù)分別表示車輛縱向速度、車輛橫向速度、轉(zhuǎn)向角速度。

履帶車輛的轉(zhuǎn)向動力學(xué)模型為

圖1 履帶車輛轉(zhuǎn)向動力學(xué)分析圖Fig.1 Steering dynamics of a tracked vehicle

式中:FL、FR分別為左、右側(cè)的牽引力(力值為負(fù)時為制動力);FfL、FfR分別為左、右的行駛阻力;m 為履帶車輛質(zhì)量;g 為重力加速度;Fc為橫向阻力;J 為車輛繞Oz 軸的轉(zhuǎn)動慣量;B 為履帶中心距;M為地面總轉(zhuǎn)向阻力矩。

此外，還有以下關(guān)系式:

式中:TL、TR分別為左、右主動輪的阻力轉(zhuǎn)矩;r 為主動輪半徑;f 為地面行駛阻力系數(shù);fK為迎風(fēng)阻力和履帶功率耗散的等效阻力系數(shù)。

履帶車輛的運動是依靠履帶推進(jìn)的，履帶的運動是由主動輪驅(qū)動的，主動輪出現(xiàn)轉(zhuǎn)速差時，車輛就能產(chǎn)生相應(yīng)的轉(zhuǎn)向角速度。因此，主動輪才是實際的轉(zhuǎn)向運動被控對象，建立兩側(cè)主動輪上微分方程:

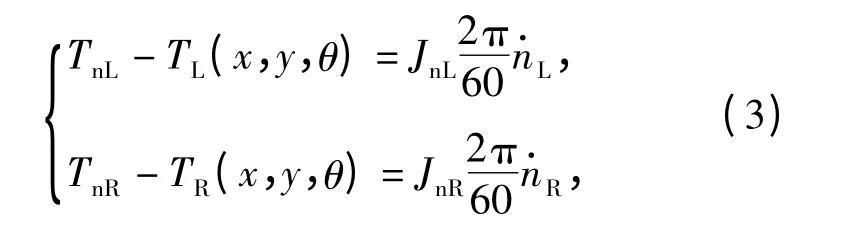
式中:TnL、TnR分別為傳動系統(tǒng)傳遞至左、右主動輪的驅(qū)動轉(zhuǎn)矩;nL、nR分別為左、右主動輪的轉(zhuǎn)速;JnL，JnR分別為左、右主動輪的轉(zhuǎn)動慣量。

1.2 雙電機耦合驅(qū)動運動學(xué)和動力學(xué)關(guān)系

履帶車輛雙電機耦合驅(qū)動系統(tǒng)，由左右兩側(cè)驅(qū)動電機、耦合機構(gòu)(中央3 個行星排)組成，如圖2所示。電機帶動耦合機構(gòu)旋轉(zhuǎn)，利用耦合機構(gòu)差速差矩功能，調(diào)節(jié)兩側(cè)主動輪的驅(qū)動轉(zhuǎn)矩以適應(yīng)地面阻力，并在主動輪上形成速度差，實現(xiàn)車輛轉(zhuǎn)向。其中:kL、kR、kO分別為左、右兩側(cè)普通排及中間雙星復(fù)合排的特征參數(shù)，且kL=kR=k，kO=1;nmL、nmR分別為左、右電機的轉(zhuǎn)速;TmL、TmR分別為左、右電機的輸出轉(zhuǎn)矩;ic為側(cè)傳動比。

根據(jù)行星傳動運動學(xué)和動力學(xué)關(guān)系，在耦合機構(gòu)作用下，可得如圖2 所示的雙電機耦合驅(qū)動系統(tǒng)的運動學(xué)、動力學(xué)關(guān)系:

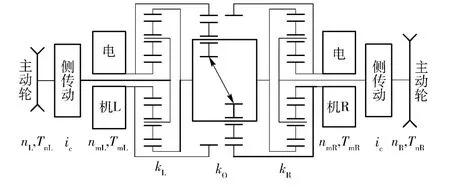
圖2 雙電機耦合電驅(qū)動系統(tǒng)圖Fig.2 System structure of double motor coupling drive transmission

轉(zhuǎn)向控制的目標(biāo)就是通過控制兩電機的轉(zhuǎn)矩TmL、TmR，使左、右兩側(cè)主動輪轉(zhuǎn)速nL、nR能跟蹤其期望轉(zhuǎn)速，從而驅(qū)動履帶車輛實現(xiàn)預(yù)定的轉(zhuǎn)向目標(biāo)。

2 轉(zhuǎn)向系統(tǒng)解耦及控制結(jié)構(gòu)分析

履帶車輛轉(zhuǎn)向的控制是根據(jù)踏板、方向盤等駕駛操縱信號決定的期望車速v*、期望轉(zhuǎn)向角速度ω*，以及反饋而來的主動輪轉(zhuǎn)速nL、nR，解算出兩電機的目標(biāo)轉(zhuǎn)矩指令經(jīng)由前述分析，方程(1)式中x、y、θ 均較難觀測，屬于不確定的參數(shù)，不同工況下轉(zhuǎn)向阻力矩難以實時預(yù)測，這就使得履帶車輛轉(zhuǎn)向系統(tǒng)具有多輸入多輸出(MIMO)、非線性耦合且參數(shù)不確定的特點。如圖3 所示。

圖3 原系統(tǒng)開環(huán)控制結(jié)構(gòu)圖Fig.3 Open loop control structure of the original system

為此，須進(jìn)行系統(tǒng)解耦，以降低控制狀態(tài)變量的耦合關(guān)聯(lián)度。根據(jù)雙電機耦合驅(qū)動履帶車輛轉(zhuǎn)向系統(tǒng)運動學(xué)關(guān)系，可通過以下狀態(tài)變換設(shè)計系統(tǒng)解耦算法。

式中:vn即為經(jīng)由主動輪轉(zhuǎn)速變換得到的車速;ωn為相應(yīng)的轉(zhuǎn)向角速度。解耦同時，對系統(tǒng)其他參量做同步線性變換。

可將控制系統(tǒng)的動力學(xué)模型變換為

其中各項阻力為

Fn、Mn則可由履帶車輛轉(zhuǎn)向行駛理論計算，其中μ是轉(zhuǎn)向阻力系數(shù)，由尼基金計算模型［6］得到。

通過變換后的新系統(tǒng)的控制解耦拓?fù)浣Y(jié)構(gòu)如圖4 所示。

圖4 新系統(tǒng)開環(huán)控制拓?fù)浣Y(jié)構(gòu)圖Fig.4 Open loop control structure of the new system

解耦后的等效開環(huán)控制結(jié)構(gòu)如圖5 所示。

從解耦新系統(tǒng)的開環(huán)結(jié)構(gòu)來看，狀態(tài)變量之間的耦合作用大大減弱，原MIMO 系統(tǒng)近似變換為兩個單輸入單輸出(SISO)的控制系統(tǒng):一為車速控制系統(tǒng);二為轉(zhuǎn)向角速度控制系統(tǒng)。

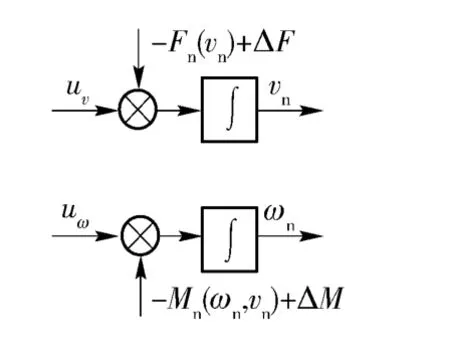
圖5 解耦后的等效開環(huán)控制結(jié)構(gòu)Fig.5 Equivalent open loop control structure of the decoupled system

解耦后的系統(tǒng)轉(zhuǎn)向運動控制目標(biāo)為:調(diào)節(jié)系統(tǒng)的等效轉(zhuǎn)矩輸入(uv、uω)T，使運動狀態(tài)(vn、ωn)T跟蹤期望的(v*、ω*)T。由(8)式可知狀態(tài)vn將影響狀態(tài)ωn的變化情況，而狀態(tài)ωn不影響狀態(tài)vn. 所以，將控制策略設(shè)計為:先針對v*完成vn的跟蹤控制;隨后將控制所得的vn視作已知參量，并針對ωn完成ω*的跟蹤控制。

3 控制算法設(shè)計

由于狀態(tài)vn將在一定程度上影響狀態(tài)ωn的變化情況，而狀態(tài)ωn不影響狀態(tài)vn. 所以，控制時可以先穩(wěn)定當(dāng)前車速即保持主動輪轉(zhuǎn)速和不變，再調(diào)節(jié)轉(zhuǎn)向角速度即調(diào)節(jié)兩側(cè)主動輪轉(zhuǎn)速差。這恰與履帶車輛差速式轉(zhuǎn)向的特點［7］相吻合。但新系統(tǒng)仍然具有一定的非線性和參數(shù)不確定性問題。滑模變結(jié)構(gòu)控制方法，具有較強的魯棒性控制特點，再加上綜合設(shè)計的模糊及自適應(yīng)算法，特別適合于解決前述系統(tǒng)的控制問題。

3.1 車速魯棒滑模變結(jié)構(gòu)控制算法設(shè)計

設(shè)計車速的魯棒滑模控制算法為

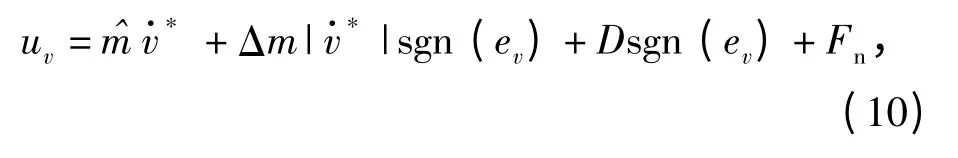
式中:

而mmax和mmin分別為慣量mn的上下界，可以預(yù)估或離線仿真確定。D 為滿足下式的任意非零正數(shù):

車速控制系統(tǒng)的Lyapunov 函數(shù)可取為

顯然該函數(shù)是正定的。且有

說明系統(tǒng)穩(wěn)定，車速跟蹤誤差有界。

3.2 轉(zhuǎn)向角速度自適應(yīng)模糊滑模控制算法設(shè)計

解耦后得到的轉(zhuǎn)向角速度控制系統(tǒng)中，Jn、Mn、ΔM 均未知，難以進(jìn)行精確數(shù)學(xué)描述。三者雖然具有界限，但是在不同車速、轉(zhuǎn)向角速度時其值波動較大，直接采用強制界限約束的經(jīng)典滑模控制，極易產(chǎn)生較強抖振，系統(tǒng)控制不穩(wěn)定。根據(jù)文獻(xiàn)［8 -10］，可將模糊邏輯系統(tǒng)及自適應(yīng)控制方法引入到經(jīng)典的滑模變結(jié)構(gòu)控制當(dāng)中。

定義轉(zhuǎn)向角速度的跟蹤誤差為

定義積分滑模面

理想的最優(yōu)控制算法應(yīng)為

由于Mn和Jn未知，可設(shè)計模糊邏輯系統(tǒng)逼近

模糊輸入設(shè)計為兩個參量:s2，vn. 采用高斯型隸屬函數(shù)，其一般形式為

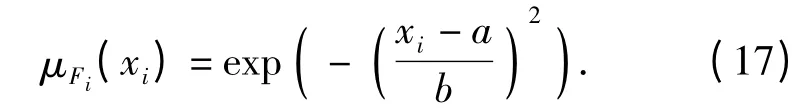
模糊規(guī)則的形式設(shè)計為

Rule:IF s2isvnisTHEN u is θl，其中:為模糊控制器輸入量的模糊子集;θ =［θ1，θ2，…，θl］為模糊規(guī)則庫中規(guī)則中的“則”部分對應(yīng)的模糊集合的中心。輸出量的反模糊化采用中心解模糊進(jìn)行，為便于后文討論，定義模糊集向量ξ=［ξ1，ξ2，…，ξm］T作為輸出子集中心的權(quán)重，則有

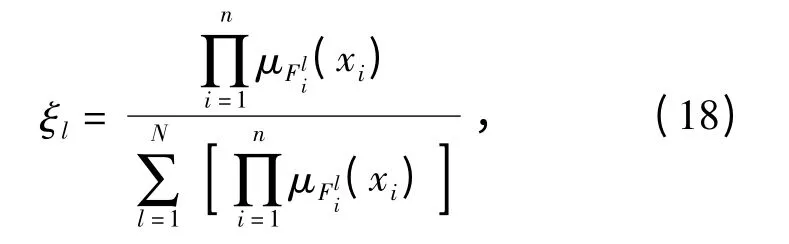
則該模糊邏輯系統(tǒng)所實現(xiàn)的模糊控制算法為

當(dāng)取定可調(diào)參數(shù)為最優(yōu)的θ*時，模糊算法的控制量uωf(θ*)將逼近，但仍然會有誤差ε，有

實際控制中，由于路面條件在變化，難以準(zhǔn)確地找到θ*. 因此，采用其估計值即實際的模糊控制輸出應(yīng)當(dāng)為

對于偏差ε，設(shè)計切換控制算法uωs來消除。

式中:H ＞εmax.

因此，轉(zhuǎn)向角速度控制算法為

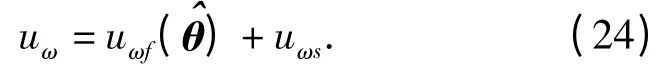
穩(wěn)定性證明如下:

定義Lyapunov 函數(shù)

式中:β 為預(yù)定的正實數(shù)。

整理狀態(tài)方程和滑動模態(tài)方程可知

總有

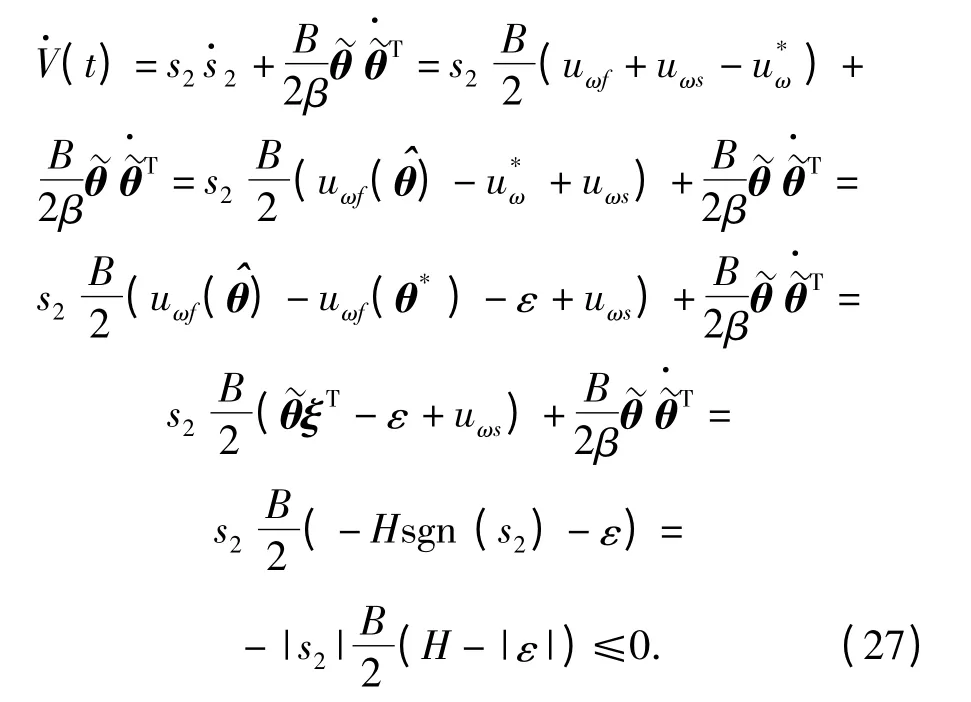
顯然，系統(tǒng)是穩(wěn)定的。

3.3 系統(tǒng)控制結(jié)構(gòu)

綜上所述，設(shè)計的雙電機耦合驅(qū)動履帶車輛控制結(jié)構(gòu)如圖6 所示。對于任意給定的期望車速v*、期望轉(zhuǎn)向角速度ω*，都可以根據(jù)車速控制系統(tǒng)的魯棒滑模控制算法求解出uv，根據(jù)轉(zhuǎn)向角速度控制系統(tǒng)的自適應(yīng)模糊滑模控制算法求解出uω，最終線性映射出電機的期望轉(zhuǎn)矩指令控制電機完成合理的轉(zhuǎn)矩輸出，實現(xiàn)轉(zhuǎn)向目標(biāo)跟蹤控制。

4 控制算法實時仿真與實驗驗證

圖6 雙電機耦合驅(qū)動閉環(huán)轉(zhuǎn)向控制結(jié)構(gòu)Fig.6 Closed loop control structure of the double motor coupling drive transmission

為了驗證控制算法的可行性和可實現(xiàn)性，通過搭建“駕駛員—控制器”［11］在環(huán)雙電機耦合驅(qū)動履帶車輛實時仿真系統(tǒng)(見圖7)，進(jìn)行控制算法的實時驗證。

操縱系統(tǒng)(方向盤、踏板)、綜合控制器為實物;建立電機及其變頻器、耦合機構(gòu)等機械系統(tǒng)以及履帶車輛等動態(tài)模型，運行在dSPACE 系統(tǒng)中DS4302進(jìn)行實時模擬;控制算法通過代碼自動生成，下載到綜合控制器。通過操縱系統(tǒng)將駕駛員操作指令轉(zhuǎn)換為輸入信號輸入綜合控制器，綜合控制器運行控制算法求得兩個電機的目標(biāo)轉(zhuǎn)矩指令，通過CAN 總線發(fā)送給dSPACE 中運行的動態(tài)模型，進(jìn)行控制算法的實時仿真驗證。

圖7 雙電機耦合驅(qū)動履帶車輛實時仿真系統(tǒng)Fig.7 Real time simulation system of the double motor coupling drive tracked vehicle

在柏油路(μmax取0.49，f 取0.038)路面下，通過油門踏板和方向盤配合，進(jìn)行車輛轉(zhuǎn)向?qū)崟r仿真。

圖8 踏板和方向盤信號Fig.8 Signals of accelerator pedal and steering wheel

圖9 左側(cè)電機的目標(biāo)轉(zhuǎn)矩及輸出轉(zhuǎn)矩Fig.9 Target torque and output torque of left motor

圖10 右側(cè)電機的目標(biāo)轉(zhuǎn)矩及輸出轉(zhuǎn)矩Fig.10 Target torque and output torque of right motor

仿真過程進(jìn)行了4 次不同轉(zhuǎn)速、轉(zhuǎn)向角速度的轉(zhuǎn)向?qū)嶒灒鐖D8 ～圖12 所示。第1 次轉(zhuǎn)向目標(biāo)車速10.0 km/h，目標(biāo)轉(zhuǎn)向角速度0.32 rad/s 對應(yīng)相對轉(zhuǎn)向半徑為3.0，實驗時車速穩(wěn)定在9.7 km/h，達(dá)到轉(zhuǎn)向角速度0.31 rad/s，實現(xiàn)的相對轉(zhuǎn)向半徑為3.1;第2 次轉(zhuǎn)向目標(biāo)車速17.0 km/h，目標(biāo)轉(zhuǎn)向角速度0.37 rad/s 對應(yīng)相對轉(zhuǎn)向半徑為4.5，實驗時車速穩(wěn)定在16.7 km/h，達(dá)到轉(zhuǎn)向角速度0.35 rad/s，實現(xiàn)的相對轉(zhuǎn)向半徑為4.7;第3 次轉(zhuǎn)向目標(biāo)車速24.0 km/h，目標(biāo)轉(zhuǎn)向角速度0.30 rad/s 對應(yīng)相對轉(zhuǎn)向半徑為8.0，實驗時車速穩(wěn)定在23.7 km/h，達(dá)到轉(zhuǎn)向角速度0.29 rad/s，實現(xiàn)的相對轉(zhuǎn)向半徑為8.2;第4 次轉(zhuǎn)向目標(biāo)車速40.0 km/h，目標(biāo)轉(zhuǎn)向角速度0.19 rad/s 對應(yīng)相對轉(zhuǎn)向半徑為21.0，實驗時車速穩(wěn)定在39.2 km/h，達(dá)到轉(zhuǎn)向角速度0.19 rad/s，實現(xiàn)的相對轉(zhuǎn)向半徑為21.9.

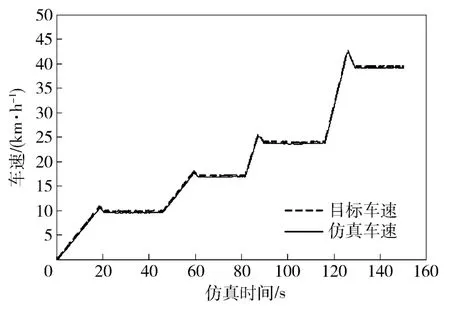
圖11 目標(biāo)車速及仿真車速Fig.11 Target and simulation forward speeds

圖12 目標(biāo)轉(zhuǎn)向角速度及仿真轉(zhuǎn)向角速度Fig.12 Target and simulation steering angular speeds

通過仿真過程可以看出:1)應(yīng)用“駕駛員—控制器”在環(huán)雙電機驅(qū)動履帶車輛實時仿真很好地驗證了轉(zhuǎn)向控制算法的可實現(xiàn)性;2)通過采用自適應(yīng)滑模轉(zhuǎn)向控制策略，解算左右電機轉(zhuǎn)矩目標(biāo)，實現(xiàn)了對車速控制目標(biāo)、轉(zhuǎn)向角速度控制目標(biāo)的精確跟蹤，具有很好的控制效果。

5 結(jié)論

1)提出了一種履帶車輛雙電機耦合驅(qū)動轉(zhuǎn)向動力學(xué)的解耦算法，將原來的雙輸入雙輸出、非線性耦合系統(tǒng)解耦為兩個SISO 系統(tǒng)，在不改變系統(tǒng)動力學(xué)特性的情況下，降低了參數(shù)之間的耦合作用，有利于控制律的設(shè)計。

2)基于解耦所得車速控制系統(tǒng)和轉(zhuǎn)向角速度控制系統(tǒng)，分別設(shè)計了自適應(yīng)模糊滑模控制算法，仿真結(jié)果證明其能實現(xiàn)車速和轉(zhuǎn)向角速度的穩(wěn)定控制。

3)在車速較高時，車速和轉(zhuǎn)向角速度的控制誤差比車速較低時要大，這是轉(zhuǎn)向離心力增大的影響結(jié)果。因此，控制律還應(yīng)針對此作進(jìn)一步的改進(jìn)。

References)

［1］史青錄.電傳動履帶車輛轉(zhuǎn)向動力學(xué)特性研究［D］. 北京:北京理工大學(xué)，2007:1.SHI Qing-lu. Study on dynamic characteristics of electric tracked vehicle on steering［D］. Beijing:Beijing Institute of Technology，2007:1. (in Chinese)

［2］孫逢春，張承寧. 裝甲車輛混合動力電傳動技術(shù)［M］.北京:國防工業(yè)出版社，2008.SUN Feng-chun，ZHANG Cheng-ning. Technologies for the hybrid electric drive system of armored vehicle［M］.Beijing:National Defense Industry Press，2008. (in Chinese)

［3］蓋江濤，李慎龍，周廣明，等. 一種履帶車輛機電復(fù)合傳動裝置:中國，CN101985279A［P］.2011-11-02.GAI Jiang-tao，LI Shen-long，ZHOU Guang-ming，et al. A type of electro-mechanical transmission for tracked vehicle:China，CN101985279A［P］.2011-11-02. (in Chinese)

［4］翟麗，孫逢春，谷中麗.電子差速履帶車輛轉(zhuǎn)向轉(zhuǎn)矩神經(jīng)網(wǎng)絡(luò)PID 控制［J］.農(nóng)業(yè)機械學(xué)報，2009，40(2):1 -4.ZHAI Li，SUN Feng-chun，GU Zhong-li. Neural networks PID control of steering torque for electronic differential tracked vehicle［J］.Transactions of the Chinese Society for Agricultural Machinery，2009，40(2):1 -4. (in Chinese)

［5］劉翼，毛明，馬曉楓，等.零差速電傳動履帶車輛轉(zhuǎn)向負(fù)載自適應(yīng)控制策略研究［J］.車輛與動力技術(shù)，2013(1):7 -11.LIU Yi，MAO Ming，MA Xiao-feng，et al. Research on self-adaptive steering control strategy for single motor cross drive electric transmission for tracked vehicles［J］. Vehicle ＆ Power Technology，2013(1):7 -11. (in Chinese)

［6］LIU Long，ZHAI Li，F(xiàn)ENG Hui-xia. Effects of dynamic characteristics of motor on steering dynamics of electric drive tracked vehicle［J］.Journal of Beijing Institute of Technology:English Edition，2011，20(2):149 -156.

［7］Wong J Y，Chiang C F. A general theory for skid steering of tracked vehicles on firm ground［J］. Proceedings of the Institution of Mechanical Engineers，2001，215(3):343 -355.

［8］劉金琨. 滑模變結(jié)構(gòu)控制MATLAB 仿真［M］. 北京:清華大學(xué)出版社，2005，379 -387.LIU Jin-kun. Sliding mode control design and MATLAB simulation［M］. Beijing:Tsinghua University Press，2005:379 -387. (in Chinese)

［9］王聲遠(yuǎn)，霍偉.不確定非完整動力學(xué)系統(tǒng)的自適應(yīng)模糊滑模控制器［J］.控制理論與應(yīng)用，2003，20(3):427 -431.WANG Sheng-yuan，HUO Wei. Adaptive fuzzy sliding-mode controllers of uncertain dynamic nonholonomic systems［J］. Control Theory ＆ Applications，2003，20(3):427 -431. (in Chinese)

［10］劉金琨，孫富春.滑模變結(jié)構(gòu)控制理論及其算法研究與進(jìn)展［J］.控制理論與應(yīng)用，2007，24(3):407 -418.LIU Jin-kun，SUN Fu-chun. Research and development on theory and algorithms of sliding mode control［J］. Control Theory ＆Applications，2007，24(3):407 -418. (in Chinese)

［11］鄒淵，孫逢春，張承寧.電傳動履帶車輛“駕駛員——綜合控制器”在環(huán)的雙側(cè)驅(qū)動控制實時仿真［J］機械工程學(xué)報，2007，43(3):193 -198.ZOU Yuan，SUN Feng-chun，ZHANG Cheng-ning. Electric tracked vehicle real-time simulation of dual-motor driving control with driver-global controller in-loop［J］. Chinese Journal of Mechanical Engineering，2007，43(3):193 -198. (in Chinese)