彈性力學(xué)平面問題的幾種解法
明星 沈強
(鄭州大學(xué) 土木工程學(xué)院,河南 鄭州 450001)
彈性力學(xué)作為固體力學(xué)的一個重要分支,它是研究彈性固體由于受外力作用,邊界約束或者溫度改變及其他一種或多種外界條件作用下產(chǎn)生的應(yīng)力、應(yīng)變和位移。它的研究對象是板、殼、實體以及單根桿件。可以說彈性力學(xué)是材料力學(xué)問題的精確解,是結(jié)構(gòu)力學(xué),塑性力學(xué)等力學(xué)學(xué)科的基礎(chǔ),其廣泛應(yīng)用于土木工程、航空航天工程及機械工程等多個學(xué)科領(lǐng)域。并且隨著科學(xué)技術(shù)手段的進步,電子計算機得以應(yīng)用到彈性力學(xué)的計算分析中,這極大地促進了彈性力學(xué)問題的分析計算更加深入,促使了有限單元法得以實現(xiàn)。因此本文從彈性力學(xué)最基本的平面問題出發(fā),通過求解平面問題的解析法、數(shù)值法和試驗方法來感受彈性力學(xué)研究問題的手段、方法,體會彈性力學(xué)的魅力,并為其它力學(xué)學(xué)科的學(xué)習(xí)打下基礎(chǔ)。
1 解析法
解析法是根據(jù)研究對象在結(jié)構(gòu)中的靜力平衡條件,幾何關(guān)系和物理關(guān)系建立邊界條件,平衡微分方程,幾何方程和物理方程,并以此求解應(yīng)力分量,應(yīng)變分量和位移分量的一種平面問題的精確解法。按求解時的基本未知量選取不同可分為按位移求解的位移法和按應(yīng)力求解的應(yīng)力法。
(1)位移法:以位移為基本未知量時的基本方程如下
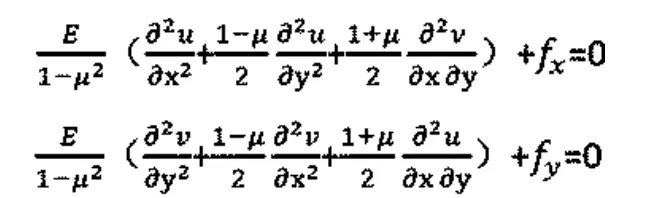
位移邊界條件如下
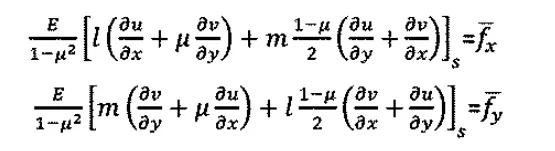
從上面的公式可以看出位移法求解平面問題時的基本未知量只有兩個,與應(yīng)力法的三個基本未知量相比求解簡單很多,并且不但能求解位移邊界條件,還能求解應(yīng)力邊界條件與混合邊界條件。
(2)應(yīng)力法:應(yīng)力法以應(yīng)力分量作為基本未知量,由此平面問題的平衡微分方程,幾何方程,物理方程以及邊界條件經(jīng)過推導(dǎo)可變?yōu)槿缦滦问剑?/p>
基本方程:
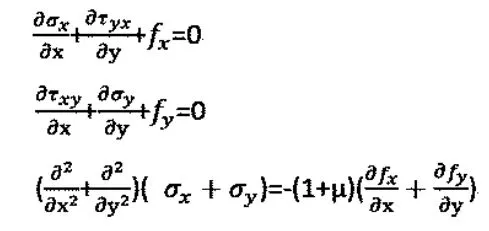
應(yīng)力邊界條件:

值得注意的是按應(yīng)力求解時邊界條件應(yīng)全部為應(yīng)力邊界條件。對于位移邊界條件,雖然在局部邊界上可用圣維南定理轉(zhuǎn)化為應(yīng)力邊界條件,但此時得到的解答已不是精確解,同時上述推導(dǎo)過程是基于平面應(yīng)力問題的,對于平面應(yīng)變問題應(yīng)把彈性常數(shù)作相應(yīng)調(diào)整。
2 數(shù)值解法
彈性力學(xué)平面問題的解法雖然針對某些問題來說可以得到精確解,但是其不適合實際工程中復(fù)雜問題的計算。相反的,數(shù)值分析方法雖然只是對實際問題的近似解答,但其求解時的過程清晰,步驟明確,便于編程,并且工程上常有安全系數(shù)的保證,因此近似解與不會對實際工程造成太大影響。從而使數(shù)值分析方法在工程問題中得到大量應(yīng)用。數(shù)值分析方法有以下三種:
差分法:用差分方程替代平衡微分方程,將求解微分方程變?yōu)榍蠼獯鷶?shù)方程,簡化了計算。
變分法:變分法其實是一種能量法,以外力所做的功及彈性體的應(yīng)變勢能來建立彈性力學(xué)的求解方程。其中基本未知量為彈性體的虛位移,運用的基本原理為虛位移原理和最小勢能原理。
有限單元法:在力學(xué)模型上進行近似將彈性體簡化為有限個單元體,且各單元體之間僅在有限個結(jié)點處交鉸結(jié)而成的結(jié)構(gòu)物。然后進行單元分析,形成單元剛度矩陣,進行整體分析,集成整體剛度矩陣,并運用矩陣位移法求解。有限單元法便于編程,因此隨著電子計算機技術(shù)的發(fā)展得以廣泛應(yīng)用于工程實踐的各個方面。相關(guān)軟件有ANSYS、ADINA、MSC、ABAQUS。
3 實驗的方法
除了解析法和數(shù)值分析方法外,工程上常用的簡單實用的方法還有實驗法。將彈性體貼上應(yīng)變片,連接上計算機便可以輕松模擬計算彈性體的內(nèi)力分布情況。
4 結(jié)論
彈性力學(xué)問題求解的解析法,數(shù)值分析方法和實驗法各有千秋,應(yīng)結(jié)合具體的工程實際問題選用合適的方法。同時也應(yīng)認識到目前彈性力學(xué)求解方法并不完善,在工程中中仍有許多問題還無法得到令人滿意的結(jié)果。因此學(xué)習(xí)掌握彈性力學(xué)的現(xiàn)有方法,并結(jié)合科學(xué)技術(shù)的發(fā)展和認識了解的加深提出新的,更加符合實際工程要求的彈性力學(xué)求解方法才是彈性力學(xué)研究的根本目的所在。

