材料維氏硬度儀器化壓入方法準確度研究

馬德軍，王家梁，肖富君，孫 亮，黃 勇

（1.裝甲兵工程學院機械工程系，北京 100072；2.總裝備部南京軍事代表局，江蘇 南京 210024）

材料維氏硬度儀器化壓入方法準確度研究

馬德軍1，王家梁1，肖富君2，孫 亮1，黃 勇1

（1.裝甲兵工程學院機械工程系，北京 100072；2.總裝備部南京軍事代表局，江蘇 南京 210024）

針對儀器化壓入測試識別材料維氏硬度的精度問題，該文采用有限元數值分析方法獲得不同材料的維氏硬度理論計算值，以此為基礎，分別對儀器化壓入識別材料維氏硬度的3種代表性方法——“ISO方法”、“Kang方法”和“Ma方法”進行理論精度分析，并進行實驗驗證。結果表明：1)3種方法識別的維氏硬度理論誤差均隨材料比功We/Wt增加呈先減小后增大的趨勢；其中，“ISO方法”識別的維氏硬度值相比理論值普遍偏大，“Kang方法”識別的維氏硬度值相比理論值均偏小。2)“Ma方法”基于儀器化壓入識別材料維氏硬度的理論誤差最小，理論準確度相對較高。3)當被測材料的材料比功在0.01＜We/Wt＜0.3時，對應η和n不同取值下的3種方法各自識別的維氏硬度誤差值較為離散；當0.3＜We/Wt＜0.85時則較為集中。該文工作，為下一步研究維氏硬度儀器化壓入新方法提供一定的理論基礎。

儀器化壓入；維氏硬度；有限元數值分析；理論準確度

0 引 言

目前，傳統維氏硬度[1-5]的測量需要通過準確量取壓痕對角線的長度獲得，對于壓痕形貌不清晰的被測材料（如圖1所示)，往往存在無法準確識別維氏硬度的問題。儀器化壓入測試[6-12]因其無需量取壓痕形貌參數，因此可以方便地確定被測材料的儀器化壓入硬度[13-14]。然而，在儀器化壓入硬度與傳統維氏硬度的關系問題以及如何將儀器化壓入硬度轉換為傳統維氏硬度的研究中，一部分通過儀器化壓入響應定義等效維氏硬度，其并不代表傳統意義的維氏硬度值[15-17]；另一部分基于實驗數據建立儀器化壓入硬度與維氏硬度的經驗關系[18-21]。因此，不同儀器化壓入識別材料維氏硬度方法的準確度問題以及方法的選擇問題值得研究并亟待解決。

圖1 最大壓入載荷為100N時的SiC試樣維氏壓痕形貌

鑒于上述情況，本文基于有限元數值分析方法獲得不同材料的維氏硬度理論計算值，以此為基礎，分別對儀器化壓入測試識別材料維氏硬度的3種代表性方法——“ISO方法”[15]、“Kang方法”[18-19]和“Ma方法”[21]進行理論準確度分析，并通過5種金屬和5種陶瓷材料對3種維氏硬度識別方法進行儀器化壓入實驗，從而進一步對本文準確度分析結論進行驗證。

1 儀器化壓入識別材料維氏硬度的方法

儀器化壓入硬度由Oliver W C和Pharr G M[13-14]在1992年提出，是目前商用儀器化壓入儀中廣泛采用的硬度指標。其定義為

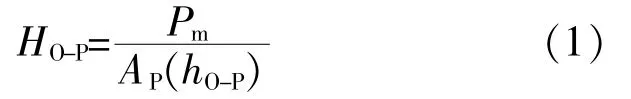
式中：Pm——儀器化壓入過程中最大壓入載荷；

hO-P——O-P接觸深度；

AP（hO-P)——O-P接觸深度hO-P時壓頭橫截面積。

O-P硬度的測試方法為：利用儀器化壓入儀及Vickers或Berkovich壓頭對被測材料實施某一最大壓入載荷為Pm的儀器化壓入測試，獲得壓入載荷-位移曲線，如圖2所示。其中，hm為最大壓入深度，Su為對應最大壓入深度hm時的初始卸載斜率，Wt與We分別為壓頭在加載和卸載過程所做的功，其值分別為加載曲線和卸載曲線與載荷-位移曲線橫坐標所圍面積；利用冪函數關系P=α（h-hf)m對卸載曲線進行擬合獲得擬合系數α、hf和m，據此計算Su=mPm（α/Pm)1/m及O-P接觸深度hO-P=hm-0.75Pm/Su，最終通過式（1)計算HO-P。

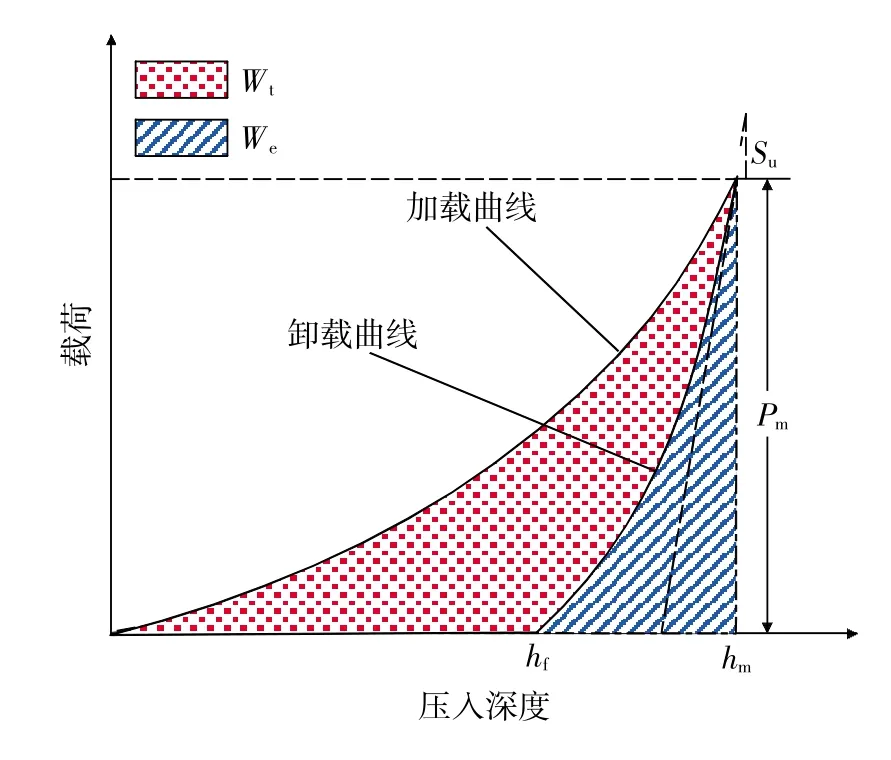
圖2 儀器化壓入載荷-位移曲線示意圖

根據儀器化壓入硬度的定義，儀器化壓入識別材料維氏硬度的方法被陸續提出：

2002年，國際標準ISO14577-1——2002[15]將最大壓入載荷Pm與對應O-P接觸深度hO-P時的Vickers或Berkovich壓頭表面積（AS（V)（hO-P)或AS（B)（hO-P))的比值當作傳統維氏硬度，其表達式為

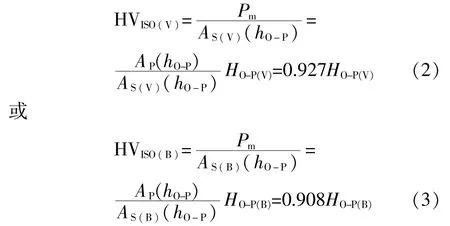
式中：HO-P（V)——基于Vickers壓頭的儀器化壓入O-P硬度；

HO-P（B)——基于Berkovich壓頭的儀器化壓入O-P硬度。

2010年，Kang S K等[18-19]對24種金屬材料進行了儀器化Vickers壓入測試和維氏硬度試驗，將測量獲得的壓痕對角線長度d轉換為Vickers壓頭與被測材料間的接觸深度

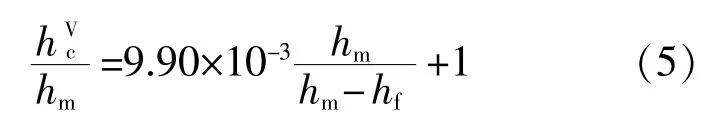
由此可以根據儀器化壓入識別材料維氏硬度，其公式為

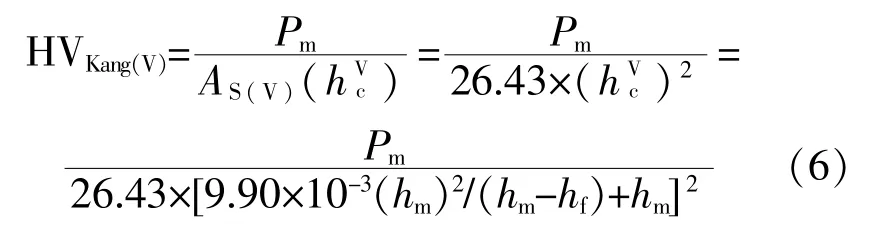
2010年，馬德軍[21]對71種鋼和5種陶瓷材料的儀器化壓入硬度與維氏硬度進行了分析，其中材料的維氏硬度由試驗獲得，71種鋼的儀器化壓入硬度由有限元數值計算獲得，5種陶瓷材料儀器化壓入硬度由實驗獲得。通過分析給出了維氏硬度與O-P硬度的近似關系為

本文將對上述3種代表性的儀器化壓入識別材料維氏硬度方法分別通過數值計算和實驗進行準確度分析。

2 數值計算

2.1 有限元模型的建立

本文運用商用有限元軟件ABAQUS[22]分別建立儀器化Vickers和Berkovich壓入三維有限元數值分析模型。因標準Vickers壓頭和Berkovich壓頭分別為面角136°正四棱錐和面角130.54°正三棱錐，為節省計算成本，根據對稱性分別取Vickers壓頭的1/8和Berkovich壓頭的1/6建立模型，如圖3陰影部分所示。同時被測材料也取與壓頭相對應的1/8和1/6。兩模型被測材料整體尺寸為4000μm×4000μm× 2000μm，壓頭最大壓入深度hm=5μm。

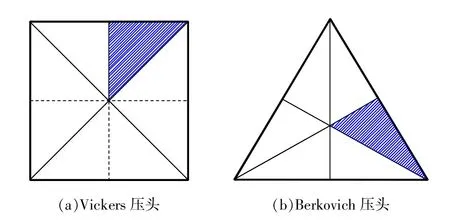
圖3 Vickers和Berkovich壓頭示意圖

定義壓頭為理想彈性壓頭，其參數設定為Ei= 1 141GPa，νi=0.07；假設被測材料為均勻、各向同性的率無關固體，考慮到幾種儀器化壓入識別維氏硬度方法的普適性，被測材料彈性模量分別取E=70，200，400 GPa，泊松比取值ν=0.3，相應的平面應變彈性模量之比η=[E/（1-0.32)]/[1141/（1-0.072)]=0.0671，0.1917，0.3834，應變硬化指數n=0，0.15，0.3，0.45；由于絕大多數工程材料比功We/Wt處于0.01～0.85之間，根據此范圍取相應的屈服強度值σy=0.98～42255MPa。壓頭與被測材料間的摩擦系數取f=0.16[23]。根據接觸核心區網格精細，遠場非核心區網格稀疏的原則，兩模型壓頭均劃分為23828個C3D4單元。對于儀器化Vickers壓入模型，被測材料劃分為51 330個C3D8R單元和158 115個C3D4單元；對于儀器化Berkovich壓入模型，被測材料劃分為46170個C3D8R單元和122847個C3D4單元，其接觸區域網格劃分如圖4所示。收斂性分析表明，兩模型網格分析誤差均不超過0.5%。整個儀器化壓入數值計算采用非線性大變形理論。

圖4 兩種儀器化壓入有限元模型局部網格圖

關于有限元數值分析模型計算材料維氏硬度的思路與文獻[24-27]接近，即當壓頭加載至最大壓入載荷Pm時，通過壓頭與被測材料間的接觸應力識別被測材料對角線方向的接觸邊緣節點；當壓頭卸載至初始位置時，將此節點與壓痕中心的最終距離作為壓痕對角線半長a，從而通過維氏硬度公式：HV=0.463 5Pm/a2，確定有限元數值計算獲得的維氏硬度理論值。

2.2 數值計算結果

分別對“ISO方法”[15]、“Kang方法”[18-19]和“Ma方法”[21]識別出的維氏硬度值進行準確度分析。

定義HVISO（V)為“ISO方法”基于Vickers壓頭計算得到的維氏硬度值，其理論誤差δISO（V)=（HVISO（V)-HV)/HV；HVISO（B)為“ISO方法”基于Berkovich壓頭計算得到的維氏硬度值，其理論誤差δISO（B)=（HVISO（B)-HV)/HV；HVKang（V)為“Kang方法”基于Vickers壓頭計算得到的維氏硬度值，其理論誤差δKang（V)=（HVKang（V)-HV)/HV；HVMa（V)為“Ma方法”基于Vickers壓頭計算得到的維氏硬度值，其理論誤差δMa（V)=（HVMa（V)-HV)/HV；由本文所建立的有限元數值分析模型計算獲得的HO-P和HV計算結果，可分別獲得對應η和n不同取值下的3種維氏硬度儀器化壓入識別方法的理論誤差隨材料比功變化的關系，即δISO（V)-We/Wt關系、δISO（B)-We/Wt關系、δKang（V)-We/Wt關系、δMa（V)-We/Wt關系，如圖5～圖8所示。

由圖可知，3種方法識別的維氏硬度理論誤差均隨被測材料比功增加呈先減小后增大的趨勢。其中，“ISO方法”識別的維氏硬度值相比理論值普遍偏大，其基于Vickers壓頭和Berkovich壓頭識別的維氏硬度最大理論誤差分別為38.1%和36.8%；“Kang方法”識別的維氏硬度值相比理論值均偏小，其基于Vickers壓頭識別的維氏硬度最大理論誤差高達-70.8%。而“Ma方法”識別的維氏硬度值相比理論值有大有小，其基于Vickers壓頭識別的維氏硬度最大理論誤差為24.6%。據此可知，“Ma方法”基于儀器化壓入識別材料維氏硬度的理論誤差最小，理論準確度相對較高。此外，當被測材料的材料比功在0.01＜We/Wt＜0.3時，對應η和n不同取值下的3種方法各自識別的維氏硬度誤差值較為離散；當0.3＜We/Wt＜0.85時則較為集中。上述結論可進一步通過實驗進行驗證。

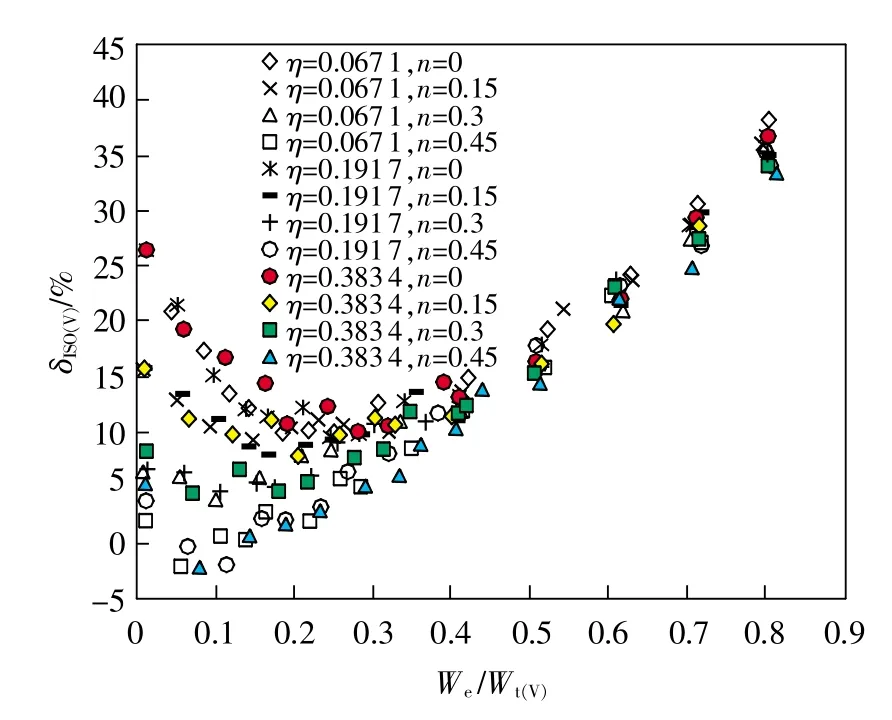
圖5 對應η和n不同取值下的δISO（V)-We/Wt關系

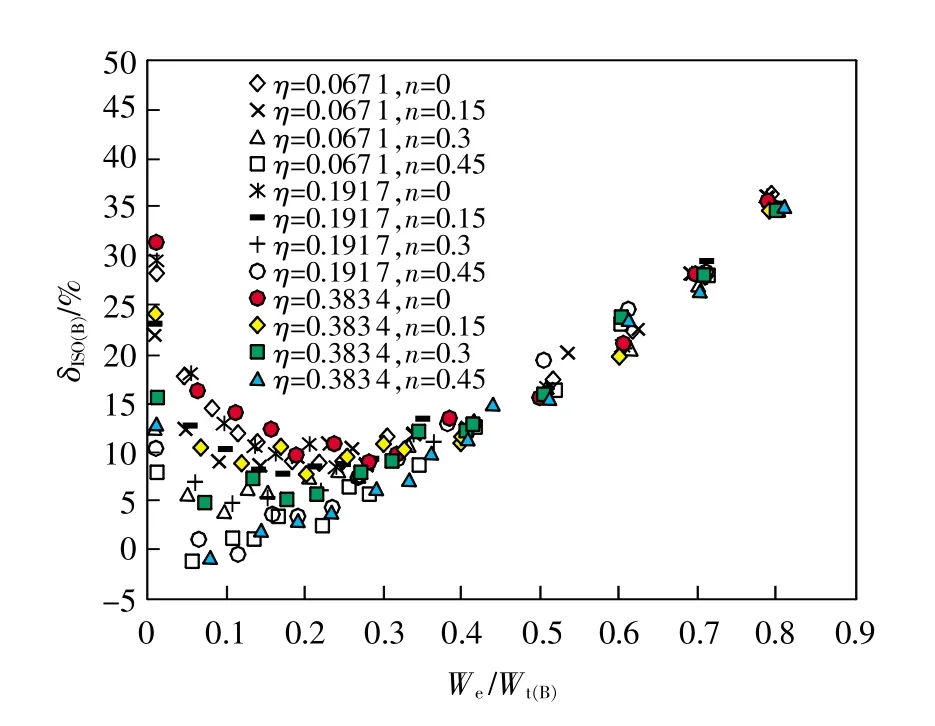
圖6 對應η和n不同取值下的δISO（B)-We/Wt關系

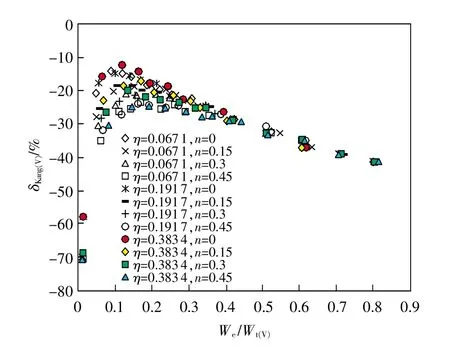
圖7 對應η和n不同取值下的δKang（V)-We/Wt關系

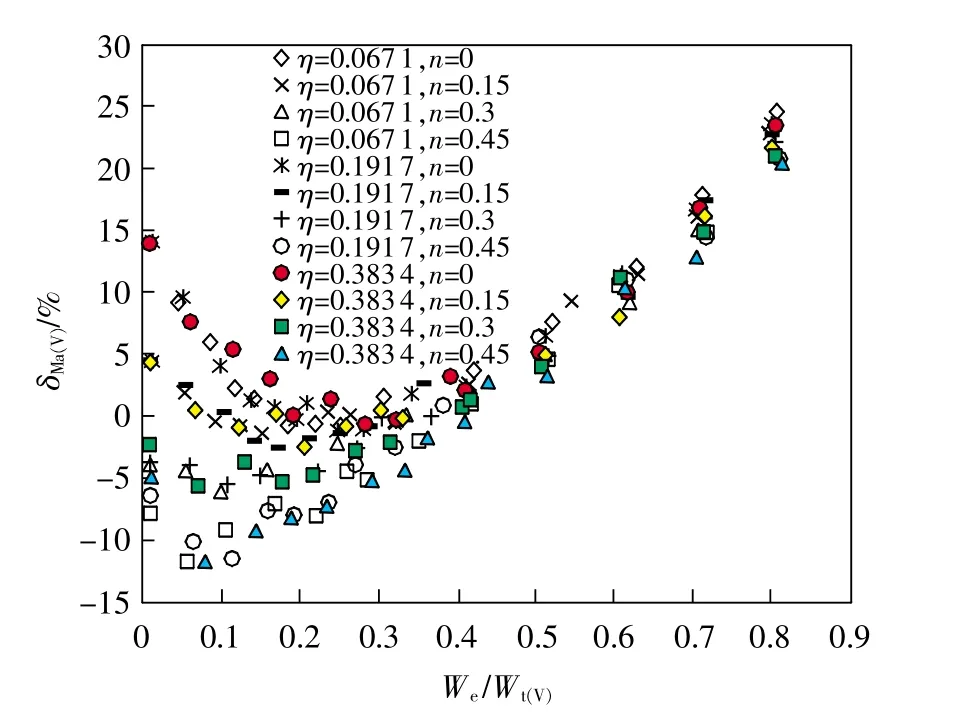
圖8 對應η和n不同取值下的δMa（V)-We/Wt關系

3 實驗驗證

本文選用5種金屬試樣（S45C、SS304、SS316、6061Al、Brass)和5種陶瓷試樣（Si3N4、ZrO2、ZTA、Al2O3、Silica)按照ISO 14577-1——2002[15]的要求制備成標準壓入試樣塊。其中，5種金屬材料由鋼鐵研究總院提供；Si3N4、ZrO2、ZTA、Al2O3試樣由中國建筑材料科學研究總院陶瓷科學研究院提供；Silica試樣為寶山鋼鐵股份有限公司提供的納米壓入儀用標準試樣（國標編號：GSB 03-2496——2008)。實驗通過本課題組前期研制的高準確度宏觀儀器化壓入儀和微觀儀器化壓入儀[28-30]在GB/T 4340.1——2009《金屬材料維氏硬度試驗第1部分：試驗方法》[31]規定的3種載荷范圍內（見表1)進行儀器化壓入測試，并通過顯微鏡測量維氏壓痕對角線半長a以獲得材料的傳統維氏硬度。以此為基礎，分別采用“ISO方法”、“Kang方法”和“Ma方法”對上述10種材料基于儀器化壓入識別的維氏硬度值與傳統維氏硬度值進行比較，從而對3種方法識別維氏硬度的準確度進行驗證。

根據表1所示 GB/T 4340.1——2009所規定的維氏硬度試驗力范圍，宏觀、小力值和顯微維氏硬度的最大壓入載荷分別設定為50，10，1N。為保證測試結果的準確性，每種材料重復測試10次。表2～表5分別為3種方法基于不同棱錐壓頭在3種載荷范圍內識別的維氏硬度均值及誤差，其中，HV為傳統維氏硬度值。

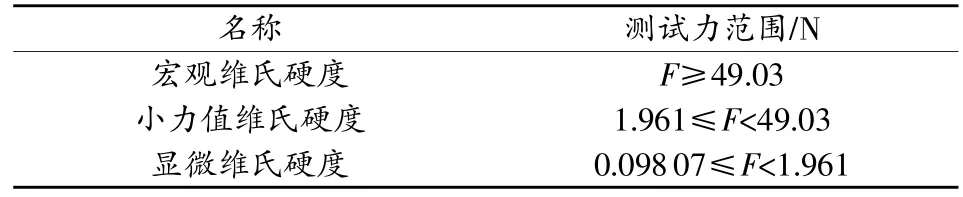
表1 維氏硬度試驗力范圍

圖9 最大壓入載荷為50N時的Silica試樣Vickers壓痕形貌圖

由表2～表5可知，“ISO方法”識別的維氏硬度值相比傳統維氏硬度值均偏大，“Kang方法”識別的維氏硬度值均偏小。除Silica試樣由于載荷過大導致壓痕形貌不清晰外（如圖9所示)，“ISO方法”、“Kang方法”和“Ma方法”對其他9種材料的宏觀維氏硬度最大識別誤差分別為：17.30%、-26.99%和5.92%；小力值維氏硬度最大識別誤差分別為：13.47%、-31.61%和-6.43%；顯微維氏硬度最大識別誤差分別為：25.95%、-34.82%和9.55%。對于Silica試樣，“ISO方法”、“Kang方法”和“Ma方法”的顯微維氏硬度最大識別誤差分別為：44.77%、-38.93%和19.77%。

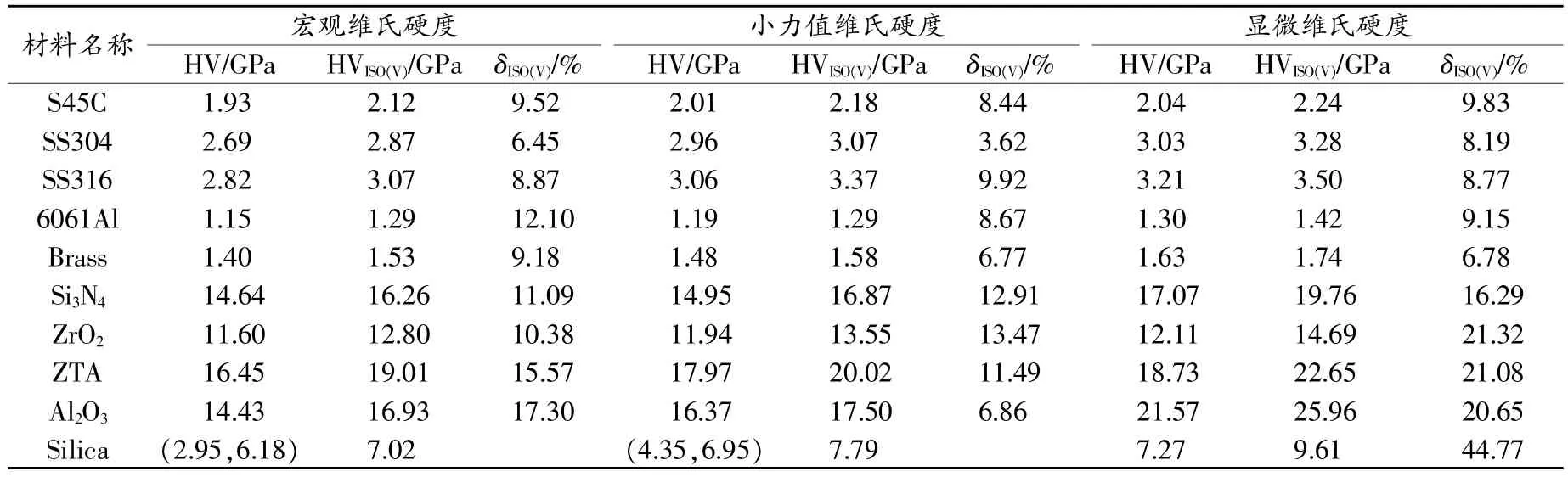
表2 “ISO方法”基于儀器化Vickers壓入識別的10種材料維氏硬度均值及誤差

表3 “ISO方法”基于儀器化Berkovich壓入識別的10種材料維氏硬度的均值及誤差

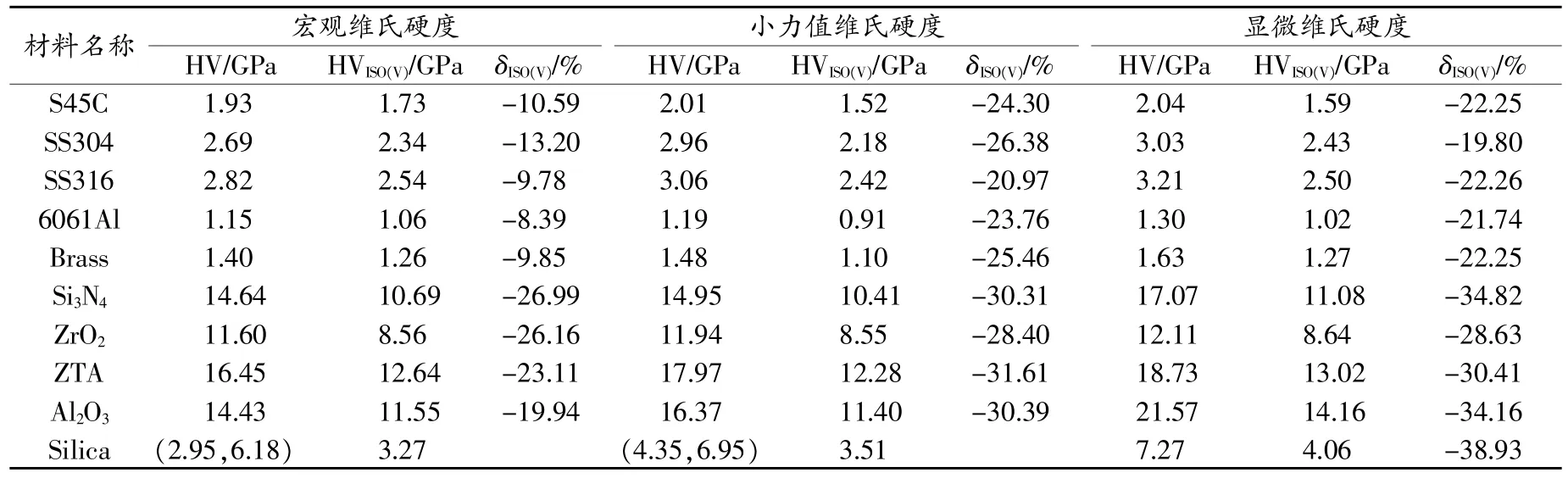
表4 “Kang方法”基于儀器化Vickers壓入識別的10種材料維氏硬度均值及誤差

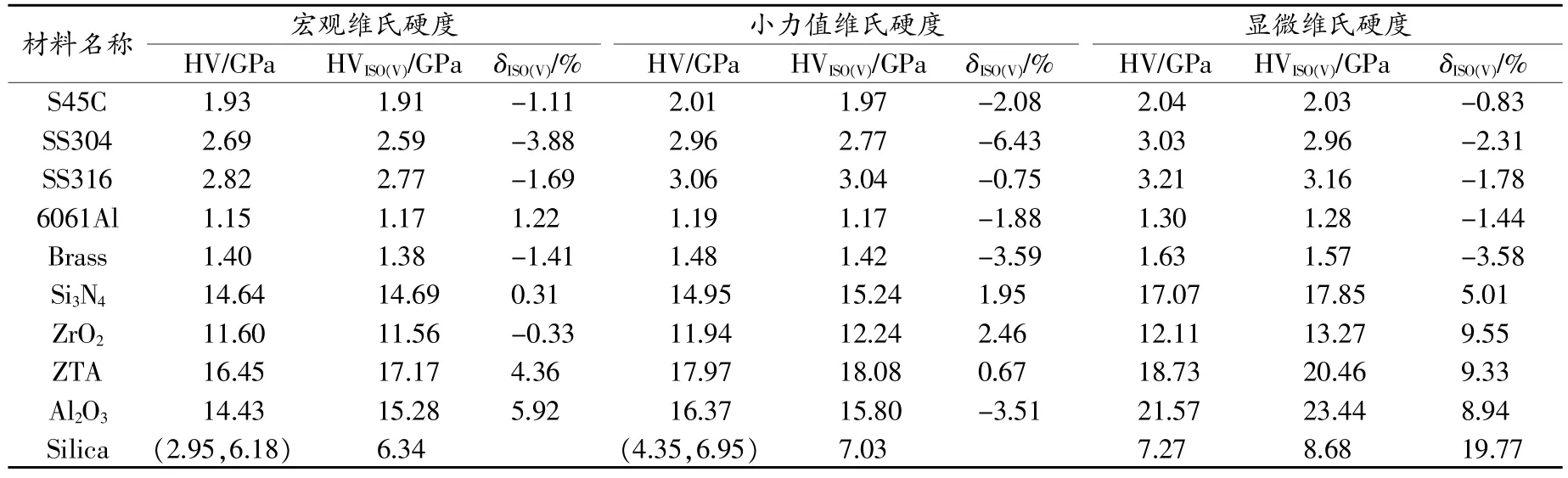
表5 “Ma方法”基于儀器化Vickers壓入識別的10種材料維氏硬度的均值及誤差

由此可知，相比其他兩種維氏硬度儀器化壓入識別方法，3種載荷下Ma方法的維氏硬度識別誤差最小，測試準確度最高。從而進一步驗證了本文通過數值計算獲得的結論。

4 結束語

本文針對儀器化壓入測試識別材料維氏硬度方法的準確度問題以及方法的選擇問題，采用有限元數值分析方法獲得不同材料的維氏硬度理論計算值，以此為基礎，分別對儀器化壓入識別材料維氏硬度的“ISO方法”、“Kang方法”和“Ma方法”進行理論準確度分析，并進行了實驗驗證，具體結論如下：

1)3種方法的維氏硬度理論誤差均隨We/Wt增加呈先減小后增大的趨勢。其中，“ISO方法”識別的維氏硬度值相比理論值普遍偏大，“Kang方法”識別的維氏硬度值相比理論值均偏小。

2)“Ma方法”基于儀器化壓入識別材料維氏硬度的理論誤差最小，理論精度相對較高。在被測材料比功We/Wt=0.01～0.85范圍內，“ISO方法”基于Vickers壓頭和Berkovich壓頭識別的維氏硬度最大理論誤差分別為38.1%和36.8%；“Kang方法”基于Vickers壓頭識別的維氏硬度最大理論誤差高達-70.8%；而“Ma方法”基于Vickers壓頭識別的維氏硬度最大理論誤差為24.6%。

3)當被測材料的材料比功在0.01＜We/Wt＜0.3時，對應η和n不同取值下的3種方法各自識別的維氏硬度誤差值較為離散；當0.3＜We/Wt＜0.85時則較為集中。本文工作，為下一步研究維氏硬度儀器化壓入新方法提供了一定的理論基礎。

[1]Tabor D.The hardness of metals[M].Oxford：Clarendon Press，1951：57-64.

[2]ISO 6507-1—2005 Metallic materials-Vickers hardness test-Part 1:Test method[S].2005.

[3]Rios C T，Coelho A A，Batista W W，et al.ISE and fracture toughness evaluation by Vickers hardness testing of an Al3Nb-Nb2Al-AlNbNi in situ composite[J].Journal of Alloys and Compounds，2009，472（1-2)：65-70.

[4]Hemalatha P，Veeravazhuthi V，Mangalaraj D.Vickers microhardness study of nonlinear optical single crystals of doped and undoped S-Benzyl isothiouronium chloride[J]. Journal of Materials Engineering and Performance，2009，18（1)：106-108.

[5]Asikuzun E，Ozturk O，Cetinkara H A，et al.Vickers hardness measurements and some physical properties of Pr2O3doped Bi-2212 superconductors[J].Journal of Materials Science：Materials in Electronics，2012，23（5)：1001-1010.

[6]Cheng Y T，Cheng C M.Scaling，dimensional analysis，and indentation measurements[R].Materials Science and Engineering，2004，44（4-5)：91-149.

[7]張泰華.微/納米力學測試技術：儀器化壓入的測量、分析、應用及其標準化[M].北京：科學出版社，2013：60-69.

[8]Sakharova N A，Oliveira M C，Antunes J M，et al.On the determination of the film hardness in hard film/substrate composites using depth-sensing indentation[J].Ceramics International，2013，39（6)：6251-6263.

[9]Ma Z S，Zhou Y C，Long S G，et al.On the intrinsic hardness of a metallic film/substrate system:Indentation size and substrate effects[J].International Journal of Plasticity，2012（34)：1-11.

[10]Chicot D，Bemporad E，Galtieri G，et al.Analysis of data from various indentation techniques for thin films intrinsic hardness modelling[J].Thin Solid Films，200 8，516（8)：1964-1971.

[11]Tuck J R，Korsunsky A M，Bhat D G，et al.Indentation hardness evaluation of cathodic arc deposited thin hard coatings[J].Surface and Coatings Technology，2001，139（1)：63-74.

[12]Chen X，Yan J，Karlsson A M.On the determination of residual stress and mechanical properties by indentation[J].Materials Science and Engineering，2006，416（1-2)：139-149.

[13]Oliver W C，Pharr G M.An improved technique for determining hardness and elastic-modulus using load and displacementsensing indentation experiments[J]. Journal of Materials Research，1992，7（6)：1564-1583.

[14]Oliver W C，Pharr G M.Measurement of hardness and elastic modulus by instrumented indentation：Advances in understanding and refinementsto methodology[J]. Journal of Materials Research，2004，19（1)：3-20.

[15]ISO14577-1—2002 Metallic materials-Instrumented indentation test for hardness and materials parameters Part 1：Test method[S].2002.

[16]邢思明.硬度標度的統一與維氏硬度試驗的數字化[J].武漢工業大學學報，2000，22（6)：43-45.

[17]邢思明，鄖建平.維氏硬度計數字化原理[J].武漢大學學報，2002，35（1)：51-54.

[18]Kang S K，Kim J Y，Park C P，et al.Conventional Vickers and true instrumented indentation hardness determined by instrumented indentation tests[J].Journal of Materials Research，2010，25（2)：337-343.

[19]Kang S K，Kim Y C，Lee J W，et al.Effect of contact angle on contact morphology and Vickers hardness measurement in instrumented indentation testing[J].International Journal of Mechanical Sciences，2014（85)：104-109.

[20]王春亮.納米壓痕試驗方法研究[D].上海：機械科學研究院，2007.

[21]馬德軍.材料力學性能儀器化壓入測試原理[M].北京：國防工業出版社，2010：219-223.

[22]Hibbitt，Karlsson.ABAQUS theory manual version 6.2[M]. Pawtucket，2000：71-86.

[23]Antunes J M，Menezes L F，Fernandes J V.Three-dimensional numerical simulation of Vickers indentation tests[J].International Journal of Solids and Structures，2006（43)：784-806.

[24]Bouzakis K D，Michailidis N，Erkens G.Thin hard coatings stress-strain curve determination through a FEM supported evaluation of nanoindentation test results[J]. Surface and Coatings Technology，2001：102-109.

[25]Bouzakis K D，Michailidis N，Hadjiyiannis S，et al. Continuous FEM simulation of the nanoindentation to determine actual indenter tip geometries,elastic-plastic materialdeformation lawsand universalhardness[J]. Zeitschrift für Metallkunde，2002（93)：862-869.

[26]Bouzakis K D，Michailidis N.Indenter surface area and hardness determination by means of a FEM-supported simulation of nanoindentation[J].Thin Solid Films，2006（494)：155-160.

[27]Bouzakis K D，Michailidis N，Skordaris G.Hardness determination by means of a FEM-supported simulation of nanoindentation and applications in thin hard coatings[J].Surface and Coatings Technology，2005（200)：867-871.

[28]宋仲康.高準確度壓入儀設計與材料力學性能測試方法研究[D].北京：裝甲兵工程學院，2011.

[29]馬德軍，郭俊宏，陳偉，等.高準確度壓入儀設計與應用[J].儀器儀表學報，2012，33（8)：1889-1896.

[30]馬德軍，宋仲康，郭俊宏，等.一種高準確度壓入儀及金剛石壓頭壓入試樣深度的計算方法：中國，CN102288500A[P].2011-12-21.

[31]GB/T 4340.1—2009金屬材料維氏硬度試驗第1部分：試驗方法[S].北京：中國質檢出版社，2009.

Study on the accuracy problems for identifying the vickers hardness by instrumented indentation method

MA Dejun1，WANG Jialiang1，XIAO Fujun2，SUN Liang1，HUANG Yong1
（1.Department of Mechanical Engineering，Academy of Armored Force Engineering，Beijing 100072，China；2.Nanjing Military Representative Bureau，General Armament Ministry，Nanjing 210024，China）

To analyize the accuracy in identifying the material’s Vickers hardness by instrumented indentation，the finite element analysis method was adopted to obtain the theoretical values of Vickers hardness of different materials.The theoretical accuracy of three representative instrumented indentation methods（ISO method，Kang method and Ma method）for identifying material’s Vickers hardness were analyzed respectively and verified experimentally.The results show that，1）The theoretical errors of the three methods in identifying material’s Vickers hardness have all been decreased at first and then increased withWe/Wt.Among them，the Vickers hardness identified by the ISO method is generally larger than the theoretical value，and that identified by the Kang method is generally smaller than the theoretical value.2）The theoretical error in Vickers hardness identified by the Ma method is the smallest but its theoretical accuracy is relatively higher compared with the other two methods.3）When 0.01＜We/Wt＜0.3，the theoretical errors in Vickers hardness indentified by these three methods are different as differentηandnvalues are taken. When 0.3＜We/Wt＜0.85，the theoretical errors are closer to each other.The analytic comarision of thispaperhasserved asa theory basisforstudying the new instrumented indentation for identifying Vickers hardnesses.

instrumented indentation；vickershardness；numericalanalysisoffinite element；theoretical accuracy

A

：1674-5124（2015）10-0006-07

10.11857/j.issn.1674-5124.2015.10.002

2014-12-16；

：2015-02-17

軍隊科研計劃項目（2014CJ011)

馬德軍（1964-)，男，山東煙臺市人，教授，博士生導師，主要從事機械力學性能測試方法研究。