基于回轉器理論的電流模式控制型 DC-DC 變流器統一大信號模型

杜韋靜 張軍明 錢照明

（浙江大學電氣工程學院 杭州 310027）

國家自 然科學基金資助項目（50907061）。

改稿日期 2013-04-14

1 引言

隨著全球范圍內對能源消耗以及環境保護的日益重視，如何高效利用能源，特別是如何利用新能源技術在世界范圍內引起了廣泛的關注。但新能源系統的大范圍接入也對傳統電網的電壓及頻率穩定性造成了影響。由于直流分布式系統能夠更容易地與新能源的輸出端口相連接，并且不包含無功分量，也不存在頻率穩定性問題，故在大力發展新能源的今天，直流分布式系統也逐漸成為業界研究的熱點。

在直流分布式系統的分析、設計過程中，穩定性問題仍是令人困擾的一大難題。盡管系統中每個變流器模塊均能夠獨立穩定運行，但模塊之間復雜的相互作用仍有可能使系統進入不穩定的工作狀態。在多模塊系統的小信號穩定性研究方面，學術界基于成熟的狀態空間平均法及其衍生出的小信號模型已經建立起較為系統的穩定性分析方法，如等效環路增益法[1]和阻抗禁止區法[2]等。然而當電路中存在大信號擾動，如啟動或大范圍負載切換時，電力電子變流器的非線性特性將凸顯，故傳統小信號模型和穩定性分析方法不再適用[3]。目前設計者大多采用計算機仿真的形式對多模塊系統的大信號穩定性進行分析。為解決大型系統仿真時間長并可能出現仿真不收斂等問題，文獻[4-8]分別基于狀態空間平均法、廣義平均法和功率守恒原理等提出了相關的仿真模型，能夠在保證一定精度的情況下大大加快系統的仿真速度。但仿真的目的主要偏重于對系統的穩定性進行驗證，無法得到解析形式的、對設計階段具有指導意義的穩定性判據或結論。

文獻[9]提出了一種適用于分岔和混沌研究的離散模型；文獻[10-13]結合現代控制理論的相關方法，如切換系統理論、分段仿射系統理論、混雜系統理論和等效小參量法等構建了相應的大信號模型。這些模型考慮了DC-DC 變流器固有的非線性特性，因此精確度較高；但模型比較復雜，大多需要借助計算機進行輔助分析，故也暫未能據此得出解析形式的穩定性判別依據。

面對越來越龐雜的系統，極有必要借助有效的建模手段，建立適合于理論分析的大信號模型，為系統的大信號穩定性設計提供具有指導意義的、解析形式的設計準則。本文結合回轉器理論和能量守恒原理，將回轉器大信號模型由Buck 變流器應用[14]推廣至所有基本拓撲及其變形得到的電路，即將回轉器模型發展為一種統一的大信號模型。該模型實現了降階，結構簡潔，輸入-輸出表達式簡單，且僅需修改一個模型參數即可實現對不同拓撲變流器的建模分析。模型的簡便性、普適性和結構統一性為理論分析系統穩定性提供了便利，也為解析形式大信號穩定性判據的提出提供了可能。同時，作為一個合格、完備的大信號模型，應當可以從中推導出原系統在任意平衡點附近的小信號特性[15]。因此，為驗證該統一大信號模型的完備性，本文對其穩態工作點附近的小信號特性進行了分析，并與目前學術界公認的、能夠較精確描述電流模式控制型變流器特性的Ridley 小信號模型進行對比，得到了較好的結果。

2 回轉器統一大信號模型原理及結構

2.1 回轉器二端口網絡簡介

在系統研究的層面上，子系統或單個變流器模塊內部的開關狀態不再是研究的重點。在不考慮損耗的前提下，根據電力電子變流器輸入功率與輸出功率相等這一特性，可考慮采用功率守恒的二端口網絡對變流器的輸入-輸出特性進行建模分析。

理想變壓器、回轉器和無損電阻是三種常見的功率守恒二端口網絡模型[16]。其中，回轉器具有電壓-電流對偶轉換功能，故較適合用于模擬電流模式控制型DC-DC 變流器的行為特性。

回轉器二端口網絡框圖如圖1 所示，其中g(t)為回轉電導。根據圖1 所示參考方向，該二端口網絡的輸入-輸出參數矩陣如式（1）～式（4）所示。

圖1 回轉器二端口網絡框圖 Fig.1 The diagram of gyrator

Uin(t)、Iin(t)、Uout(t)、Iout(t)分別為輸入-輸出電壓、電流的平均值。很容易證明，盡管計算時僅考慮參數的平均值而忽略開關紋波，但功率守恒關系仍然成立，即

2.2 統一大信號模型

基于回轉器結構為電流模式控制型DC-DC 變流器建立的統一大信號模型如圖2 所示（為簡化分析，暫不考慮斜坡補償功能）。其中，Iload(t)為負載電流，Vref為電壓環反饋網絡的參考電壓，1/H 為反饋分壓比。反饋網絡參數均與原變流器相同。

圖2 回轉器統一大信號模型結構框圖 Fig.2 The diagram of unified gyrator large-signal model

可調的回轉電導g(t)由兩個參數的乘積構成：一是反饋網絡輸出電壓u(t)。當模型輸出電壓Uout(t)改變時，g(t)會跟隨u(t)變化從而達到調整回轉器輸入/輸出電流的目的，以模擬原變流器中電流模式控制的功能。由圖2 可知，由于回轉器具有電壓-電流對偶轉換特性，可使原變流器中電壓、電流雙環控制結構得以簡化，僅采用電壓單環反饋即可實現電流模式控制的功能；構成g(t)的另一個參數k 主要用來調節變流器中被控電流所能達到的最大值，且該參數表達式與變流器拓撲有關。對于不同的DC-DC 變流器拓撲而言，其大信號模型結構均與圖2 相同，唯一的區別是參數k 的表達式不同。本文以Buck、Boost 和Buck-Boost 三種基本拓撲為例進行分析研究。

2.3 Buck 變流器大信號模型參數計算

圖3 為峰值電流模式控制Buck 變流器電路簡圖。

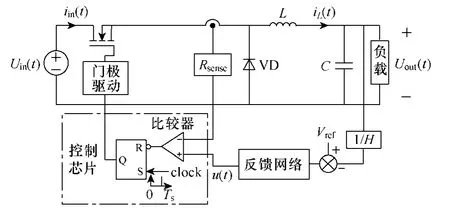
圖3 峰值電流模式控制Buck 變流器電路簡圖 Fig.3 Diagram of peak current mode controlled Buck converter

其中，Rsense為等效電流采樣電阻。對比圖2 與圖3 可知，Buck 變流器電感電流平均值IL與回轉器電流 Iout(t)相等。根據回轉器輸入-輸出關系可得Iout(t)表達式如下

假設反饋網絡輸出電壓的飽和值為usat，電感電流峰值的最大值為iLmax，則有

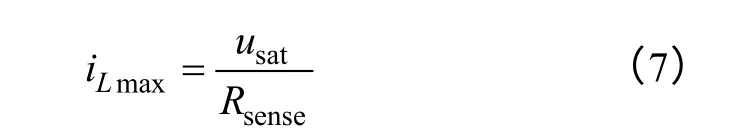
當變流器正常工作時，電感電流平均值和峰值均遠小于iLmax。而當反饋環飽和、電感電流峰值達到iLmax時，大多數變流器均工作在CCM 模式，且電感電流紋波相對于其平均值而言較小。因此可忽略該紋波以達到簡化計算的目的，即假設此時電感電流平均值的最大值IL-max=iLmax。

對大信號模型而言，當u(t)=usat時，Iout(t)也將達到其最大值Iout-max(t)，表達式如下

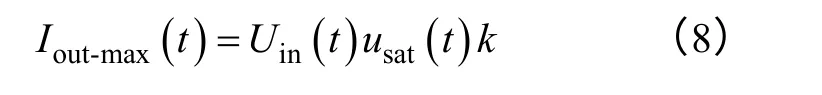
利用關系式IL-max=Iout-max，聯立式（7）和式（8），可得Buck 變流器大信號模型參數k 的表達式如下所示。

2.4 Boost 變流器大信號模型參數計算

圖4 為峰值電流模式控制Boost 變流器電路。

圖4 峰值電流模式控制Boost 變流器電路 Fig.4 Diagram of peak current mode controlled Boost converter

對比圖2 和圖4 可知，Boost 變流器電感電流平均值IL與回轉器電流Iin(t)相等。當反饋環達到飽和時，Iin(t)也將達到其最大值Iin-max(t)。根據回轉器輸入-輸出關系可得

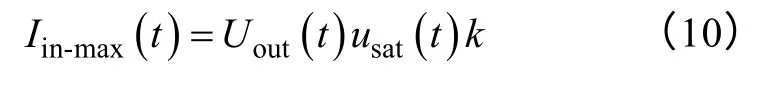
與Buck 變流器分析思路類似，忽略此時電感電流的紋波，令Iin-max(t)和iLmax相等并聯立式（7）和式（10），可得Boost 變流器大信號模型參數k 的表達式如下

2.5 Buck-Boost 變流器大信號模型參數計算

圖5 所示為峰值電流模式控制型Buck-Boost 變流器電路簡圖。

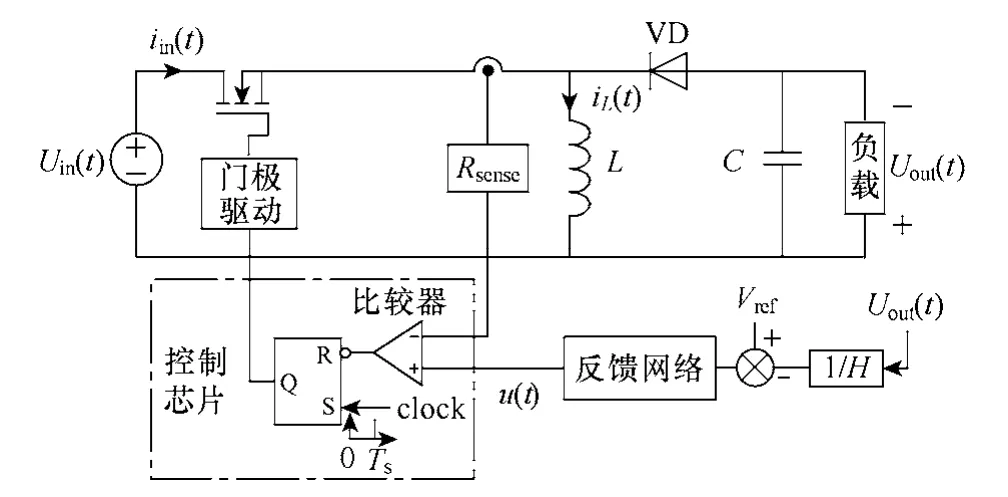
圖5 峰值電流模式控制Buck-Boost 變流器電路簡圖 Fig.5 Diagram of peak current mode controlled Buck-Boost converter

對比圖2 和圖5 可知，Buck-Boost 變流器電感電流平均值IL與回轉器電流Iin(t)和Iout(t)之和相等，即

當反饋環電壓u(t)=usat時，IL達到最大值IL-max，結合式（8）和式（10）可得

與上述分析類似，忽略此時的電感電流紋波，聯立式（7）和式（13），令IL-max與iLmax相等，可得Buck-Boost 變流器大信號模型參數k 的表達式如下：

2.6 小結

綜上所述，除反饋網絡參數外，電流模式控制DC-DC 變流器的基本拓撲均可采用圖2 所示的統一大信號模型表示。對于不同拓撲的變流器而言，大信號模型結構均保持不變，唯一的區別是參數k 的表達式不同，總結見表1。

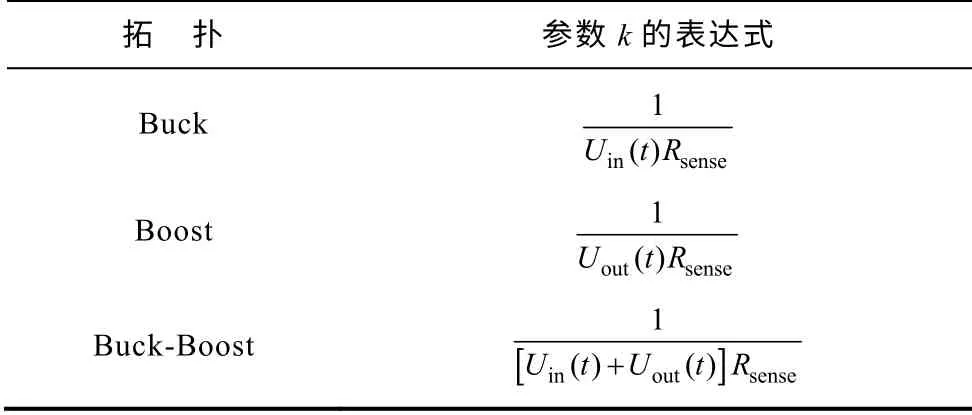
表1 三種基本拓撲下大信號模型參數k 的表達式 Tab.1 Expressions of parameter k in large-signal model for the three basic DC-DC topologies

由于該統一大信號模型的理論基礎是普適的能量守恒定律，故該模型不僅適用于上述三種DC-DC基本拓撲，還可用于描述由這些基本拓撲變化衍生出的其他DC-DC 變流器，如反激變流器等。

此外，本文提出的統一大信號模型其回轉器部分的輸入、輸出端口可看做受控電流源。輸入電壓與回轉器輸入側電流源相連，輸出側電流源與電容相連，示意圖如圖6 所示。

圖6 統一大信號模型的等效框圖 Fig.6 Equivalent diagram of the unified large-signal model

該模型在忽略電感的情況下能夠自然滿足電壓源與電流源交替相連的電路連接規則[17]，成功地實現了降階，使模型得以簡化，為后續的理論分析提供了便利。

3 仿真和實驗驗證

為驗證該統一大信號模型的有效性，分別針對峰值電流模式控制型Buck、Boost 和Buck-Boost 三種基本拓撲進行驗證。仿真和實驗中均采用純阻性負載，并對負載由20%階躍至滿載這種大信號行為進行了研究。

3.1 Buck 變流器大信號模型仿真和實驗結果

峰值電流模式控制型Buck 變流器參數如表2所示。其中，模型參數k=0.1。仿真、實驗波形如圖7 所示，參數定義與圖2 及圖3 一致。

表2 峰值電流模式控制型Buck 變流器參數表 Tab.2 Parameters of peak-current mode controlled Buck converter

圖7 Buck 變流器及統一大信號模型仿真、實驗波形圖 Fig.7 Simulation and experimental results of unified large-signal model and Buck converter

3.2 Boost 變流器大信號模型仿真和實驗結果

表3 為峰值電流模式控制型Boost 變流器參數。根據表1 可知，Boost 變流器大信號模型參數k 的取值與輸出電壓Uout有關，且該電壓在負載階躍的暫態過程中會有波動。出于簡化分析的目的，將Uout的額定電壓值30V 代入計算，得k=0.167。其仿真和實驗結果如圖8 所示。

表3 峰值電流模式控制型Boost 變流器參數表 Tab.3 Parameters of peak-current mode controlled Boost converter

圖8 Boost 變流器及統一大信號模型仿真、實驗波形圖 Fig.8 Simulation and experimental results of unified large-signal model and Boost converter

3.3 Buck-Boost 變流器大信號模型仿真和實驗結果

表4 為峰值電流模式控制型Buck-Boost 變流器參數。其仿真、實驗結果如圖9 所示。假設輸入電壓源為理想電源，且基于與3.2 節相同的簡化方法，可將Uin和Uout的額定電壓值代入計算，得模型參數k=0.04。

表4 峰值電流模式控制型Buck-Boost 變流器參數表 Tab.4 Parameters of peak-current mode controlled Buck-Boost converter

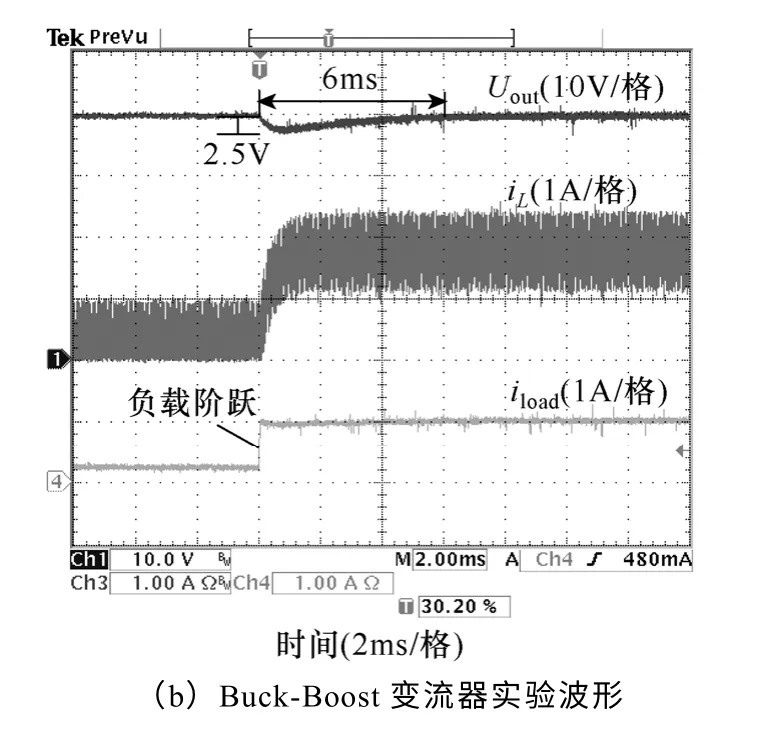
圖9 Buck-Boost 變流器及統一大信號模型仿真、 實驗波形圖 Fig.9 Simulation and experimental results of unified large-signal model and Buck-Boost converter

3.4 小結

根據上述仿真、實驗波形可知，在負載由20%階躍至滿載的暫態過程中，大信號模型的仿真波形與原變流器實驗波形相吻合。該模型能夠較好地反映峰值電流控制型Buck、Boost 及Buck-Boost 變流器的大信號特性，從而驗證了模型的有效性。

4 統一大信號模型的小信號特性分析

合格的大信號模型應包括系統在任意平衡點附近的小信號特性。為驗證該回轉器大信號模型的完備性，需對其穩態工作點附近的小信號特性進行分析。假設圖2 中所帶負載R 為純阻性負載，且輸入電壓為理想電壓源，不存在擾動。若輸入-輸出電壓、電流的穩態值分別為Uin、Uout、Iin和Iout，反饋網絡輸出電壓的穩態值為U，則在平衡點處對上述變量施加微小擾動，可得

根據回轉器網絡的輸入-輸出關系式可得

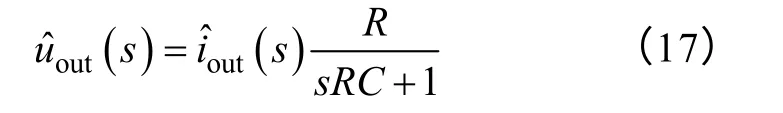
聯立式（16）和式（17）可得控制至輸出的傳 遞函數Gvu(s)如式（18）所示，其中。

統一大信號模型的環路增益Tm如式（19）所示，其中Gcv(s)為反饋網絡的傳遞函數。

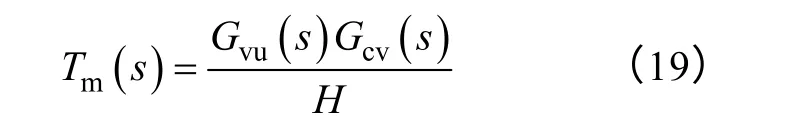
在傳統小信號模型中，Raymond B.Ridley 建立的模型是目前公認的、能夠比較準確地描述電流模式控制型DC-DC 變流器特性的小信號模型[18]。故將統一大信號模型的分析結果與Ridley 模型進行對比。圖10～圖12 分別為基于Buck、Boost 及Buck- Boost 變流器的環路增益對比結果，開關頻率均為20kHz。

圖10 基于Buck 變流器的小信號特性對比結果 Fig.10 Comparison result of small-signal characteristic based on Buck converter

圖11 基于Boost 變流器的小信號特性對比結果 Fig.11 Comparison result of small-signal characteristic based on Boost converter

圖12 基于Buck-Boost 變流器的小信號特性對比結果 Fig.12 Comparison result of small-signal characteristic based on Buck-Boost converter

由于Ridley 模型考慮了采樣保持特性，故控制信號擾動量造成的影響在至少一個開關周期后才會反映在電感電流峰值上；而統一大信號模型中，控制信號u(t)的擾動會立刻通過回轉系數影響回轉器的輸入、輸出電流值。因此低頻段統一大信號模型的增益略微高于Ridley 模型。此外，Ridley 模型中的采樣保持模塊使系統在二分之一開關頻率（10kHz）處存在兩個極點；而統一大信號模型中并未考慮采樣保持作用。故二者的特性在二分之一開關頻率處存在較大差異。但總體而言，在二分之一開關頻率以下的頻率段內，統一大信號模型的小信號特性與Ridley 模型吻合較好，進一步驗證了該大信號模型的完備性和有效性。

5 結論

本文基于回轉器理論為電流模式控制型 DC- DC 變流器建立了統一的大信號模型。該模型輸入-輸出表達式簡單，實現了降階，采用電壓單環反饋即可實現電流模式控制的功能；同時，僅需修改一個模型參數即可實現對不同拓撲變流器的建模，使分析過程大大簡化。模型的簡便性、普適性和統一性均為理論分析大信號穩定性提供了便利。仿真和實驗分別以Buck、Boost 及Buck-Boost 三種基本拓撲為例，對模型的有效性進行驗證，并得到了較好的結果。同時，為了驗證該統一大信號模型的完備性，對其穩態工作點附近的小信號特性也進行了分析，并與Ridley 模型的分析結果進行對比，二者的環路增益在二分之一開關頻率以下的頻率段內吻合較好，模型的完備性得以驗證。

[1] Middlebrook R D.Input filter considerations in design and application of switching regulators[C].Proceedings of the IEEE Industry Applications Con- ference,1976:91-107.

[2] Zhang J M,Xie X G,Jiao D Z,et al.Stability problems and input impedance improvement for cascaded power electronic systems[C].Proceedings of the IEEE Applied Power Electronics Conference and Exposition,2004:1018-1024.

[3] Erickson Robert W,Cuk Slobodan,Middlebrook R D.Large-signal modelling and analysis of switching regulators[C].Proceedings of the IEEE Power Elec- tronics Specialists Conference,1982:240-250.

[4] Liu Yanfei,Sen Paresh C.A general unified large signal model for current programmed DC-to-DC converters[J].IEEE Transactions on Power Electronics,1994,9(4):414-424.

[5] Zhou Yan,Wang Bolin.A large signal dynamic model for buck-cascaded Buck-Boost converter in universal-input PFC applications[C].Proceedings of the IEEE Electrical Machines and Systems,2008:4080-4085.

[6] Canalli V M,Cobos J A,Oliver J A,et al.Behavioral large signal averaged model for DC/DC switching power converters[C].Proceedings of the IEEE Power Electronics Specialists Conference,1996:1675-1681.

[7] Mahdavi J,Emadi A,Bellar M D,et al.Analysis of power electronic converters using the generalized state-space averaging approach[J].IEEE Transactions on Circuits and Systems,1997,44(8):767-770.

[8] 王潤新,劉進軍,侯丹.用于實現互聯系統仿真的電源模塊大信號模型[J].西安交通大學學報,2009,43(6):76-81.

Wang Runxin,Liu Jinjun,Hou Dan.Large-signal model of power supply modules for implementing inter-connected system simulations[J].Journal of Xi’an Jiaotong University,2009,43(6):76-81.

[9] 張波,李萍,齊群.DC-DC 變換器分叉和混沌現象的建模和分析方法[J].中國電機工程學報,2002,22(11):81-86.

Zhang Bo,Li Ping,Qi Qun.Methods for analyzing and modeling bifurcations and chaos in DC-DC converter[J].Proceedings of the CSEE,2002,22(11):81-86.

[10] 陸益明,張波,尹麗云.DC/DC 變換器的切換仿射線性系統模型及控制[J].中國電機工程學報,2008,28(15):16-22.

Lu Yiming,Zhang Bo,Yin Liyun.Switched affine systems modeling and control of DC/DC converters [J].Proceedings of the CSEE,2008,28(15):16-22.

[11] Tahami F,Mobed M,Molayee B.On piecewise affined large-signal modeling of PWM converters[C].Proceedings of the IEEE International Conference on Industrial Technology,2006:1419-1423.

[12] 陳明亮,馬偉明,騰方宏.HS 理論在DC/DC 變換器建模及仿真中的應用[J].電力電子技術,2007,41(3):86-88.

Chen Mingliang,Ma Weiming,Teng Fanghong.Application of hybrid system theory in modeling and simulation of DC/DC converter[J].Power Electronics,2007,41(3):86-88.

[13] 陳艷峰,丘水生.用符號法分析 PWM 開關功率變換器閉環系統的穩態[J].電子學報,2007,28(7):130-134.

Chen Yanfeng,Qiu Shuisheng.Steady-state analysis of closed-loop PWM switching power converter systems using symbolic method[J].Acta Electronica Sinica,2007,28(7):130-134.

[14] 張陽,張軍明,杜韋靜.基于回轉器的Buck 變換器大信號建模[J].電工技術學報,2011,26 (增刊1):49-55.

Zhang Yang,Zhang Junming,Du Weijing.Large- signal model by means of gyrators for buck converters [J].Transactions of China Electrotechnical Society,2011,26(Sup.1):49-55.

[15] 王潤新.用于多模塊互聯系統仿真的電力電子變流器大信號模型研究[D].西安:西安交通大學,2009.

[16] Singer Sigmunt,Erickson Robert W.Canonical mode- ling of power processing circuits based on the POPI concept[J].IEEE Transactions on Power Electronics,1992,7(1):37-43.

[17] Liu Kwang Hwa,Lee Fred C.Topological constraints on basic PWM converters[C].Proceedings of the IEEE Power Electronics Specialists Conference,1988:164- 172.

[18] Ridley Raymond B.A new,continuous-time model for current-mode control[J].IEEE Transactions on Power Electronics,1991,6(2):271-280.