兩自由度微撲翼飛行器升阻力系數分析

李德寶， 舒寧， 王洪洋

（合肥工業大學機械與汽車工程學院，合肥230009）

0 引言

微型撲翼飛行器由于運動方式獨特、靈活性強等特點，越來越受到關注。在數值理論研究方面，研究人員［1］分析了二維機翼在一定頻率范圍內推力產生的機理，研究發現在0.7 Hz附近推進效果最佳；研究人員［2］分析研究了低雷諾數下，昆蟲翅翼做非定常運動的氣動性能，發現當翅翼大攻角撲動時，對大升力的產生十分有利；研究人員［3］通過數值模擬，對昆蟲懸停時高升力機理有了更為深入的解釋。計算流體力學（簡稱CFD）分析軟件Fluent是通過數值模擬計算，對研究流體運動、熱傳遞等現象具有良好的優勢。研究人員［4］利用Fluent軟件分析比較了翅翼在三種不同拍動模式下的升力和升力系數。研究人員［5］運用Fluent軟件模擬分析了仿蜻蜓翅翼撲動時的流場特性。研究結果表明，對比以前風洞實驗等研究方法，利用Fluent軟件使空氣動力的計算變得便捷和準確，且成本低、周期短，能分析模擬不同狀態并獲得完整數據。

利用Fluent軟件，根據所設計兩自由度撲翼結構的撲動運動規律，對兩種不同撲動形式進行了二維仿真模擬，分析研究兩種拍動形式下流場特性，獲得翅翼在一個拍動周期內升阻力系數的變化情況，并進行相互間分析比較。

1 基本控制方程

在對昆蟲和鳥類的長期觀察中，研究人員發現翅膀上下撲動的過程中，不僅有上下平動，而且同時伴隨著翅翼繞某一軸線的規律轉動，可以認為是低雷諾數下的湍流流動。黏性不可壓縮流體（二維）的基本控制方程由如下兩個方程組成。

連續性方程為

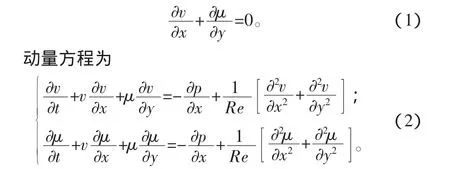
式中：p 為壓力，Pa；v為流體的速度矢量，m/s；Re 為雷諾數，常規飛行器流場雷諾數Re一般都大于106，由于撲翼飛行器在低空飛行，尺寸和飛行速度都較小，故流場雷諾數Re要比常規飛行器Re小得多，一般都在104～105以下。撲翼飛行器雷諾數按照Ellington［6］的定義，可利用翅膀的平均弦長D和平均翼尖速度V進行計算：

式中：ψ為展翅角；λ為展弦比；f為頻率；l為翅長；μ為運動黏度。

2 撲翼結構分析

采用雙曲柄雙搖桿機構，故對曲柄搖桿機構進行簡要分析。如圖1所示，在機構中，構件L1為原動件，構件L3在構件L2帶動下做往復運動，翅翼固連在構件L3上，從而實現翅翼的上下拍打運動。四桿尺寸參數如表1所示。

圖1 鉸鏈四桿機構

根據機構各桿所構成的封閉矢量多邊形，可以得出以下矢量關系式：

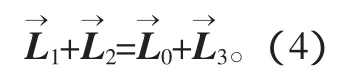
求解可得角位移分量形式為：

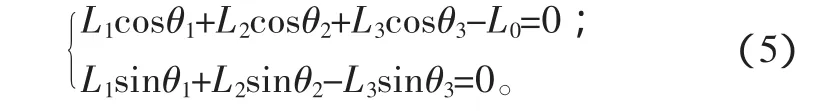
其中 θ1、θ2、θ3分別為各構件的方位角，對于給定任意一個曲柄位置θ1，均可以根據上式求出連桿和搖桿的方位角 θ2、θ3，相應的角速度和角加速度可通過求一階和二階導數得到。

在微型電機驅動下，通過減速機構，構件1以14 Hz的頻率勻速轉動時，翅翼的上下撲動角度及角速度隨時間變化規律如圖2所示，翅翼的最大撲動角和最小撲動角分別為 124°、50.37°，整個拍動幅度約為 73°。

表1 四桿機構參數mm

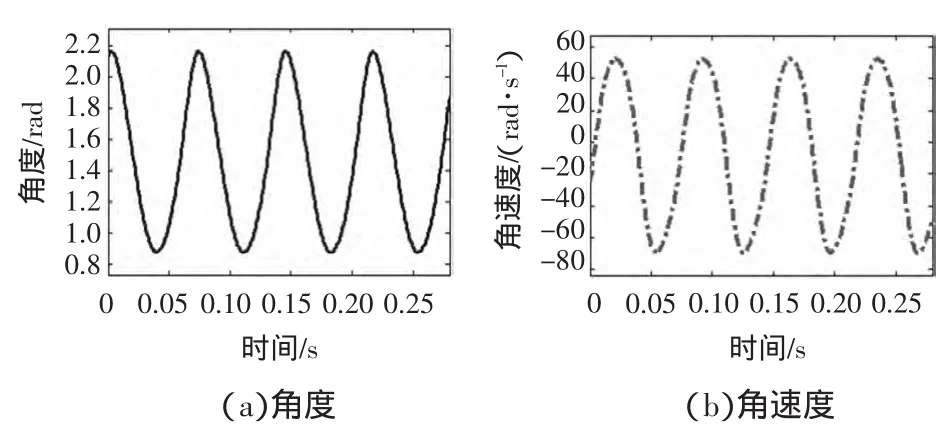
圖2 角度和角速度變化曲線

考慮到研究人員［7］所設計的轉動機構過于復雜，故在凸輪機構的基礎上引入了球形鉸鏈，有效地簡化了撲翼結構，減輕了整機重量。如圖3所示，由微電機驅動，經過減速機構帶動曲柄轉動，通過連桿傳遞實現翅翼上下往復運動，同時由于翅根處凸輪機構的轉向作用，從而使得翅翼從單一沉浮運動演變為沉浮加俯仰的兩自由度運動模式，圖4為凸輪扭轉角度變化規律，如圖所示，翅翼可以實現約為40°的扭轉。

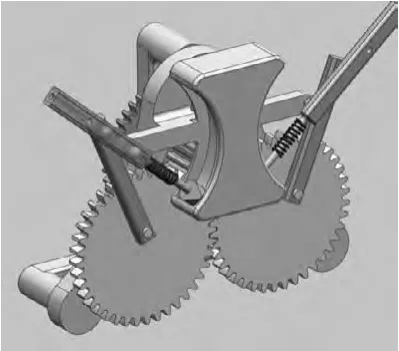
圖3 三維實體模型

圖4 凸輪扭轉角度變化曲線

3 撲動過程中的升阻力系數分析

3.1 網格劃分及動網格設置

網格劃分之前，選取合理計算區域十分關鍵，合理的求解區域將直接影響整個計算結果的準確性以及計算時間。采用橢圓面為翅翼的弦向截面，從而建立計算模型。將翼型置于800 mm×400 mm的矩形區域內，為提高網格適應性、計算精度和節約計算時間，網格采用三角形非結構化網格。利用Gambit生成網格，如圖5所示，共有30 396個節點數個，網格數為60 122個。

圖5 全局網格圖

利用CFD軟件Fluent中的用戶自定義函數（UDF），使用void DEFINE_CG_MOTION函數編譯動網格UDF文件控制翅翼的上下拍動的運動規律，從而建立所需的動態網格模型。網格更新主要有三種動網格方式：彈簧近似光滑模型、動態分層模型和局部重構模型。彈簧近似光滑模型計算精度高，但在計算區域變形較大時，會影響計算精度；動態分層模型要求與運動邊界相鄰的網格必須為楔形或者六面體網格；局部重構模型僅能用于四面體網格和三角形網格。根據翅翼模型實際運動情況綜合考慮，確定采用彈簧近似光滑模型和局部重構模型相結合的方法進行動網格的生成。

3.2 沉浮運動的升阻力系數

在FLUENT中有很多湍流模型可供選擇，在撲動過程中，翅翼的上下往復運動使得翅翼附近的空氣流動復雜多變，因此擬采用RNG k-ε模型。針對撲翼模型在流場的撲動飛行，設定無窮遠處自由來流速度U∞=3 m/s，在控制體上利用simple算法［8］對其進行數值離散。翅翼在流場中快速拍打，翼背（上表面）和翼面（下表面）產生壓力差，從而產生升阻力。升阻力系數計算公式為

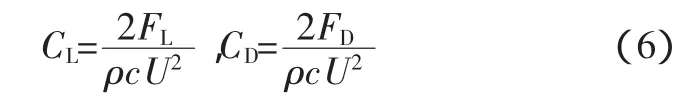
式中：ρ為空氣密度；c為翼型的弦長；U為周期內翼型表面來流平均速度。

在Fluent中，可以直接對升阻力系數進行監測，圖6為Fluent軟件求解流程圖。

圖6 Fluent求解流程圖

設定拍動頻率為14 Hz，時間步長為0.001 s，計算300個時間步長，迭代了6000次后，升阻力系數變化規律曲線如圖7所示。

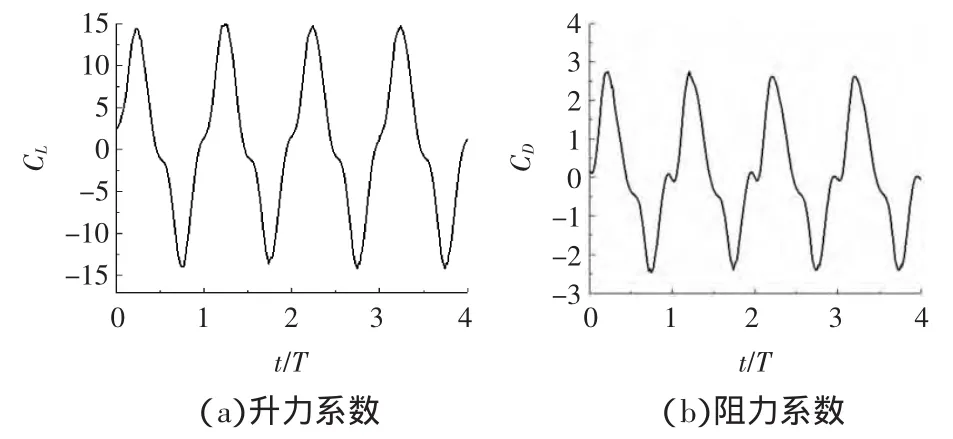
圖7 升阻力系數變化曲線

從圖中可以看出在下拍過程中，升力系數急劇增加，約在0.25T時達到了峰值，此時在上表面形成的漩渦最大，上下表面的空氣流動速度的差異使得上下表面形成了壓力差，上表面壓力小于下表面，便形成了升力。同時由于攻角存在，后緣渦強度大于前緣渦強度，表現為阻力系數的增加。上拍過程中升阻力系數變為負值。在整個拍動周期，凈升阻力系數為正值。下拍時流場速度及壓力分布如圖8～圖9所示。

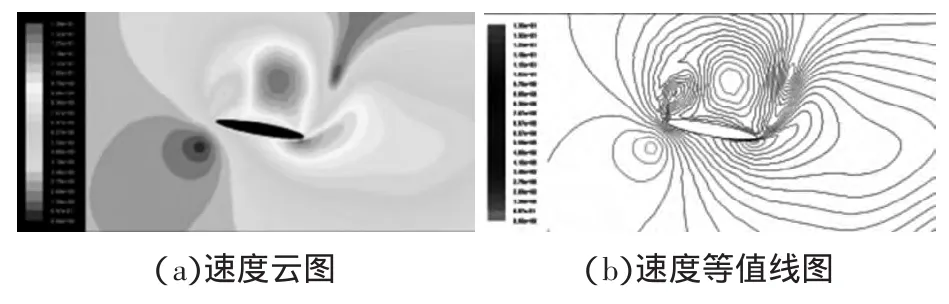
圖8 下拍時流場速度分布

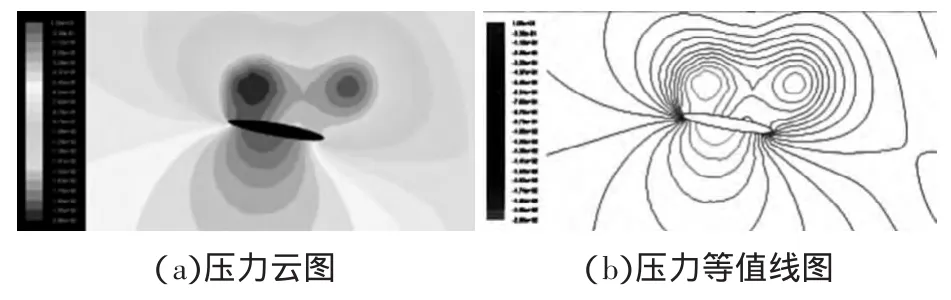
圖9 下拍時流場壓力分布

3.3 沉浮加俯仰運動的升阻力系數比較

在凸輪機構的轉向作用下，可以實現翅翼約為40°的扭轉。翅翼在下拍過程中與來流方向呈10°夾角，到最低位置時經過凸輪機構的作用，使得翅翼在上拍過程與來流方向夾角為50°。可根據仿真數據將扭轉變化規律簡化為如下方程：

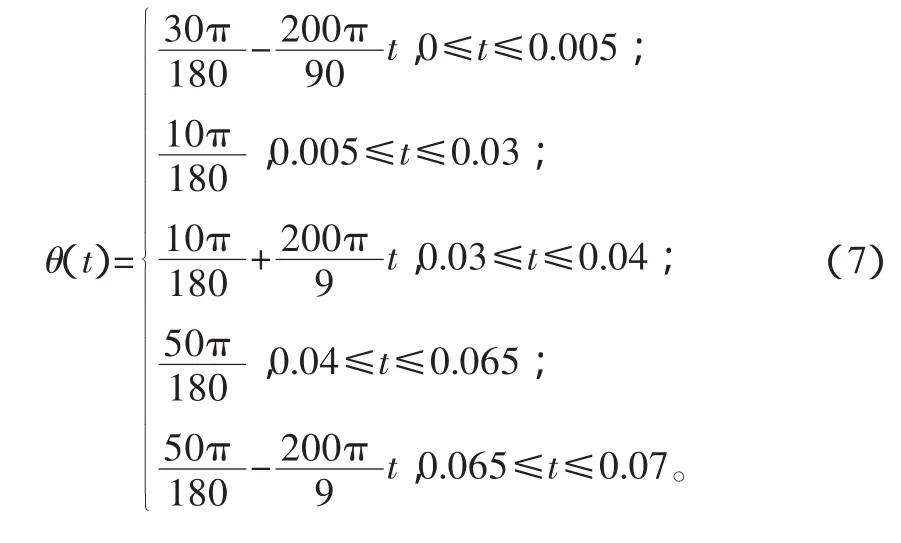
運用與上述相同的研究方法，將轉動的運動模式加入翅翼的運動中，可以得到升阻力系數的變化曲線，如圖10所示。圖中，A為沉浮運動時的升阻力系數，B為沉浮加俯仰運動時的升阻力系數，通過曲線對比可知，沉浮加俯仰運動時，上拍過程中，升力系數明顯升高，同時阻力系數也有所降低，整個拍動周期翅翼獲得的凈升力系數要大于單一的沉浮運動時的凈升力系數，凈阻力系數要小于單一沉浮運動時的凈阻力系數。上拍時流場速度與壓力分布如圖11～圖12所示。

圖10 升阻力系數對比圖

圖11 上拍時流場速度分布

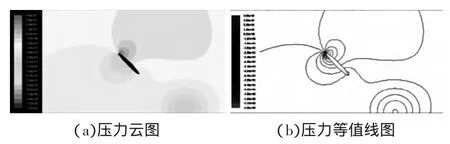
圖12 上拍時壓力流場分布

4 結論

CFD軟件Fluent可有效模擬模型翼在流場中的運動情況，所提供的自定義函數（UDF）窗口把翅翼相對復雜的運動模式轉化成可編譯的外部C程序，有效解決了數值模擬中流場N-S方程所存在的“動邊界問題”，結果表明運用Fluent軟件模擬分析流場相關特性是可靠的。

研究結果表明，翅翼在不同的運動模式下的升阻力系數存在著差異，由于凸輪轉向機構的作用，兩自由度的機構在撲動中獲得了更大的凈升力系數，同時也降低了凈阻力系數，有效增大了升力，減小了阻力。

研究局限在機構有無扭轉情況下的升阻力系數，且均采用二維簡化模型，對于具體翼型產生的影響及更復雜的撲翼運動規律還需更深入的研究。

［1］ Wang J.Vortex shedding and frequency selection in flapping flight［J］.JFluid Meeh，2000，410：323-341.

［2］ 蘭世隆，孫茂.模型昆蟲翼非定常運動時的空氣動力特性［J］.力學學報，2001，33（2）：173-182.

［3］ Sun M，Hossein H.Force and flow structures of an airfoil performing some unsteady motions at small Reynolds number［J］.Aeta Aerodyamica Siniea，2000，18（Suppl）：96-102.

［4］ 朱洪波，謝進，陳永.用Fluent分析仿生翅翼運動產生的升力和升力系數［J］.機械設計與制造，2011(5)：68-70.

［5］ 張孝松，基于蜻蜓翅翼的仿生微撲翼飛行器機翼的有限元分析［D］：哈爾濱：哈爾濱工業大學，2006.

［6］ E1lington C.The aerodynamics of hovering insect flight∶I.the quasi-steady analysis ［J］.Philosophical Transactions of the Royal Society of London B，1984,305∶1-15.

［7］ 朱寶，王姝歆.兩自由度撲翼機構及其運動仿真研究［J］.中國制造業信息化，2009,38（21）：24-28.

［8］ 周建華.微型拍翅式飛行機器人翅運動及控制系統研究［D］.南京：東南大學，2005.