J2攝動下基于平均軌道要素差的集群航天器空間圓形編隊設計

張 朔， 吳 國 強*,2

( 1.大連理工大學 工業裝備結構分析國家重點實驗室, 遼寧 大連 116024；2.大連理工大學 航空航天學院, 遼寧 大連 116024 )

J2攝動下基于平均軌道要素差的集群航天器空間圓形編隊設計

張 朔1， 吳 國 強*1,2

( 1.大連理工大學 工業裝備結構分析國家重點實驗室, 遼寧 大連 116024；2.大連理工大學 航空航天學院, 遼寧 大連 116024 )

集群航天器是通過無線連接方式構成的虛擬航天器系統，考慮J2攝動下其在太陽同步軌道的空間圓形編隊設計，對滿足其模塊間能量傳輸、數據交互的需要和應用需求具有重要意義．基于主、從模塊平均軌道要素差建立了相對運動模型，并給出了空間圓形編隊的詳細設計步驟；在零J2攝動條件不再適用時，通過定量分析J2攝動對該編隊構形的影響，提出了相應的修正公式；將模塊修正后的平均軌道要素轉換為初始時刻密切軌道要素確定了初始編隊構形．采用無奇點的新四元數軌道要素進行J2攝動分析，仿真結果驗證了設計方法的有效性．

J2攝動；平均軌道要素；集群航天器；空間圓形編隊

0 引 言

集群航天器最初由美國麻省理工學院的Mathieu等提出[1]，相較于傳統航天器，集群航天器具有在軌靈活、可擴展、可維護和可快速響應等優勢，研究集群航天器對于加快快速響應空間系統的建設速度，增強空間技術創新能力和提高新型航天器研制水平具有重要意義[2]．空間圓形編隊可高精度保持各功能模塊間相對距離，滿足集群航天器模塊間能量傳輸和數據交互的要求．太陽同步軌道則具有很高的應用價值，資源衛星、氣象衛星、軍用衛星、海洋衛星等均采用太陽同步軌道[3]．因此，研究集群航天器在太陽同步軌道的空間圓形編隊設計具有重要意義．

關于建立航天器編隊相對運動方程的方法有很多種，高云峰等提出了編隊飛行的相對軌道要素法[4]．安雪瀅則基于相對軌道要素差推導了一階相對運動模型[5]．殷建豐等通過定義新的軌道要素，推導了含有相對漂移率的相對運動方程[6]．孟鑫等推導了便于攝動分析的相對運動方程[7]．采用上述相對運動方程直接進行編隊構形設計時，都能滿足較小的構形誤差，但是在考慮地球非球形體引起的J2攝動后，無法保持構形的穩定性．平均軌道要素在編隊構形設計中通過合適的算法，可以使編隊構形更加穩定，設計的控制律更加有效，從而節省編隊構形控制的燃料消耗[8]．

本文建立以主、從模塊初始平均軌道要素差表示的相對運動方程，給出空間圓形編隊設計的詳細步驟．上述設計步驟可確定主、從模塊的初始平均軌道要素，然而在考慮J2攝動時，構形仍會遭到破壞，因此需要進行修正．在利用零J2攝動條件對模型進行修正時，僅存在零解，因此本文結合平均攝動法[9]，定量分析J2攝動對編隊構形形狀和方向的影響，進而提出相應的修正公式．將修正后的模塊的初始平均軌道要素轉換為初始密切軌道要素[10]，采用新四元數軌道要素進行攝動分析[11]．通過對比零J2攝動條件和本文修正公式的攝動仿真結果，驗證設計方法的有效性．

1 相對運動建模與構形設計

1.1 坐標系定義

為了描述集群航天器中主、從模塊間的相對運動，選取兩個參考坐標系：J2000地心赤道慣性坐標系Oe-X1Y1Z1，其中原點Oe位于地心，OeX1軸指向春分點，OeZ1軸垂直于平赤道面指向北極，OeY1軸的方向由右手定則確定；主模塊軌道坐標系Os-X2Y2Z2，Os位于主模塊質心，OsX2軸方向為主模塊質心背離地心方向，OsY2軸在主模塊軌道平面上且垂直于OsX2軸并指向飛行前方，OsZ2軸的方向由右手定則確定．

1.2 平均軌道要素與相對運動方程

(1)

其中平均軌道要素中的元素按順序分別為平均半長軸、平均軌道偏心率、平均軌道傾角、平均升交點赤經、平均近地點幅角和平均平近點角．

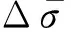
(2)

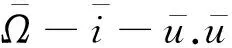
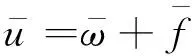
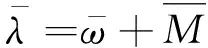
(3)

(4)

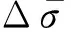
(5)

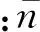
(6)

1.3 空間圓形編隊設計

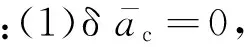
根據上述約束條件，給出空間圓形編隊的具體設計步驟：

(2)給定空間圓形編隊半徑l，求得A和C；

(3)選擇ψ=0或ψ=π，本文選取前者；

(4)給定編隊從模塊的總數，設計不同的φ，本文將φ在0至2π的范圍內均分，使得各從模塊之間相位差一致；

(6)由式(6)中A和cosφ的計算公式求得

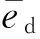
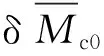
在編隊構形設計時采用的是主、從模塊于編隊初始時刻的平均軌道要素，編隊設計時尚未考慮模塊的平均軌道要素受J2攝動的影響，因此，上述編隊構形設計只適用理想情況．仍需分析攝動對編隊構形影響，然后對編隊初始時刻的平均軌道要素進行修正，來抑制攝動引起的構形變化．

2 J2攝動對編隊構形的影響及修正

2.1 一般的編隊構形的軌道平面分析

由式(5)可得一般的編隊構形所在軌道平面(繞飛軌道平面)的幾何方程：

(7)

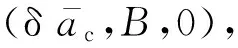
(8)

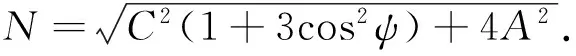
(9)

2.2 J2攝動下編隊構形的變化

根據平均攝動法[9]，平均軌道要素在J2攝動影響下的攝動方程為

(10)

式中：J2為帶諧系數，Re為地球半徑，μ為地球引力常數．分別計算主、從模塊的平均軌道要素變化率時只需在上式中替換相對應的變量即可．

由前文知，從模塊與主模塊的平均軌道要素差為小量，近似為一階變分關系，對從模塊與主模塊的平均軌道要素變化率之差也作近似一階變分處理，結合式(10)推得

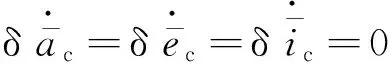
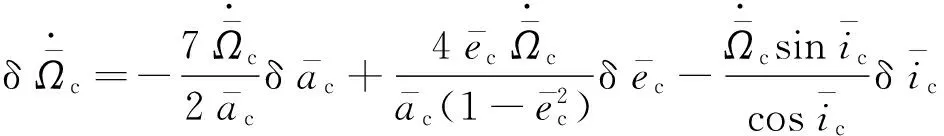
(11)

根據主模塊的初始時刻平均軌道要素和編隊構形要求設計得到的從模塊的初始平均軌道要素，雖然在初始時刻滿足構形要求，但是考慮J2攝動的影響后，隨著主、從模塊的飛行，約束條件就不再精確滿足，下面分析編隊構形受J2攝動的影響情況．

(12)

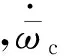
(13)

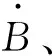
2.3 平均軌道要素的修正公式

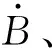
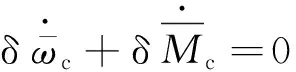
(14)

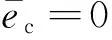
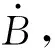
(15)

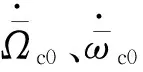
2.4 軌道要素的轉換及攝動方程

將修正后的主、從模塊的初始平均軌道要素轉換為初始密切軌道要素后，通過求解攝動方程，可計算編隊構形隨時間的變化．由歐拉角定義的經典軌道要素存在奇異性；而改進的春分點軌道要素雖然避免了奇異性，但存在繁瑣的三角函數計算．本文采用新四元數軌道要素表示的攝動方程[11]．

3 仿真算例及結果分析

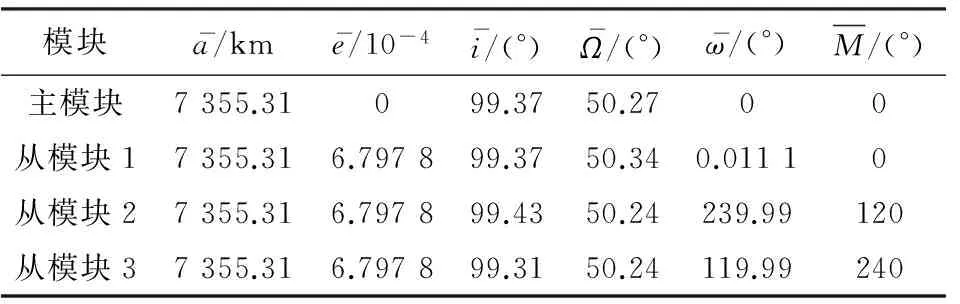
表1 模塊初始時刻的平均軌道要素Tab.1 Initial mean orbital elements of modules

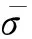
表2 從模塊的平均軌道半長軸修正量Tab.2 Revised values for mean orbital semi-major axis of deputy modules

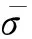
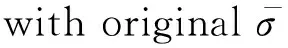
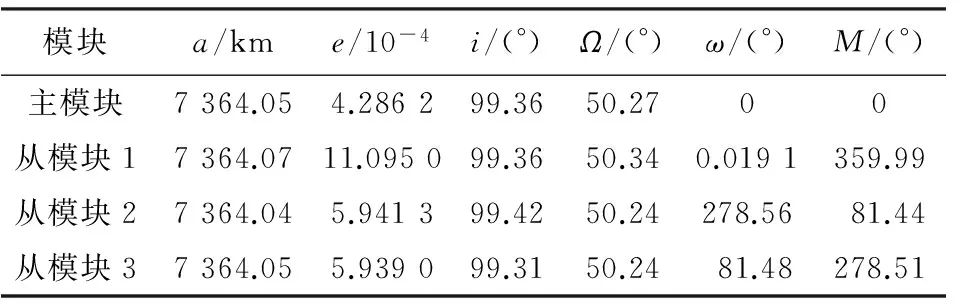
模塊a/kme/10-4i/(°)Ω/(°)ω/(°)M/(°)主模塊7364.054.286299.3650.2700從模塊17364.0711.095099.3650.340.0191359.99從模塊27364.045.941399.4250.24278.56081.44從模塊37364.055.939099.3150.24081.48278.51

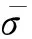
表4 修正與未修正的從模塊初始密切軌道要素之差Tab.4 The difference between revised and unrevised osculating orbital elements of deputy modules

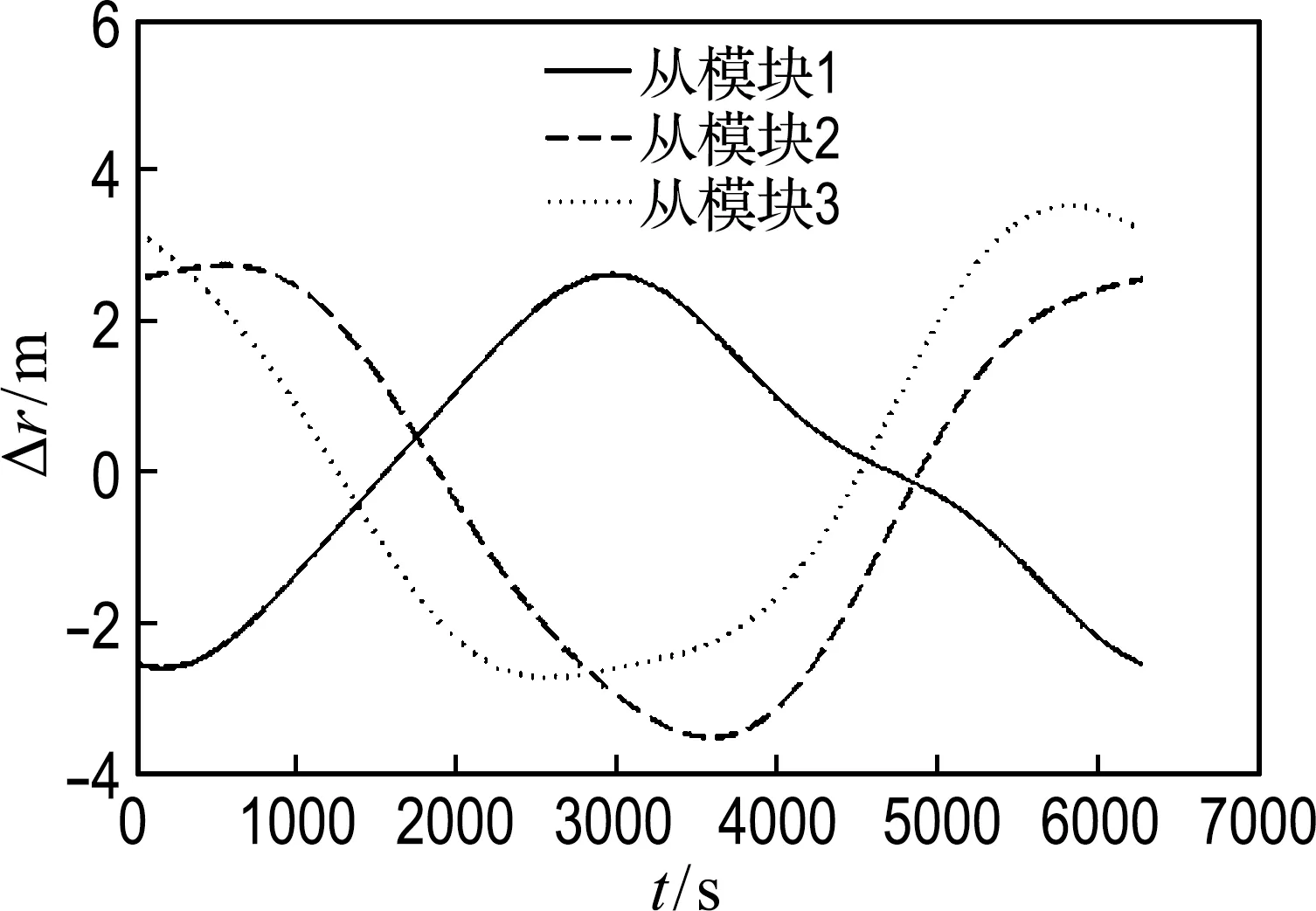
圖1 無J2攝動時編隊構形的相對位置誤差Fig.1 Relative position error of formation configuration without J2 perturbation

由圖1可知，在不考慮J2攝動時，實際編隊飛行中與繞飛半徑10 km的理想空間圓形的位置誤差僅在4 m左右，驗證了本文相對運動模型的有效性．考慮J2攝動時，對比圖1與圖3(a)知，編隊構形發生了較大改變，相對位置誤差隨飛行時間逐漸增大，在3個交點周期已達到近300 m．由圖3(a)與圖3(b)對比可知，從模塊1的相對位置誤差并沒有減小，因為兩者同平均軌道傾角，故無須修正，但其他從模塊的相對位置誤差從300 m減少至150 m，驗證了本文的修正公式可有效抑制繞飛軌道的跡向漂移．由圖2可知，各從模塊之間相位差相同，并在中心為主模塊、半徑為10 km的空間圓形軌道上飛行．

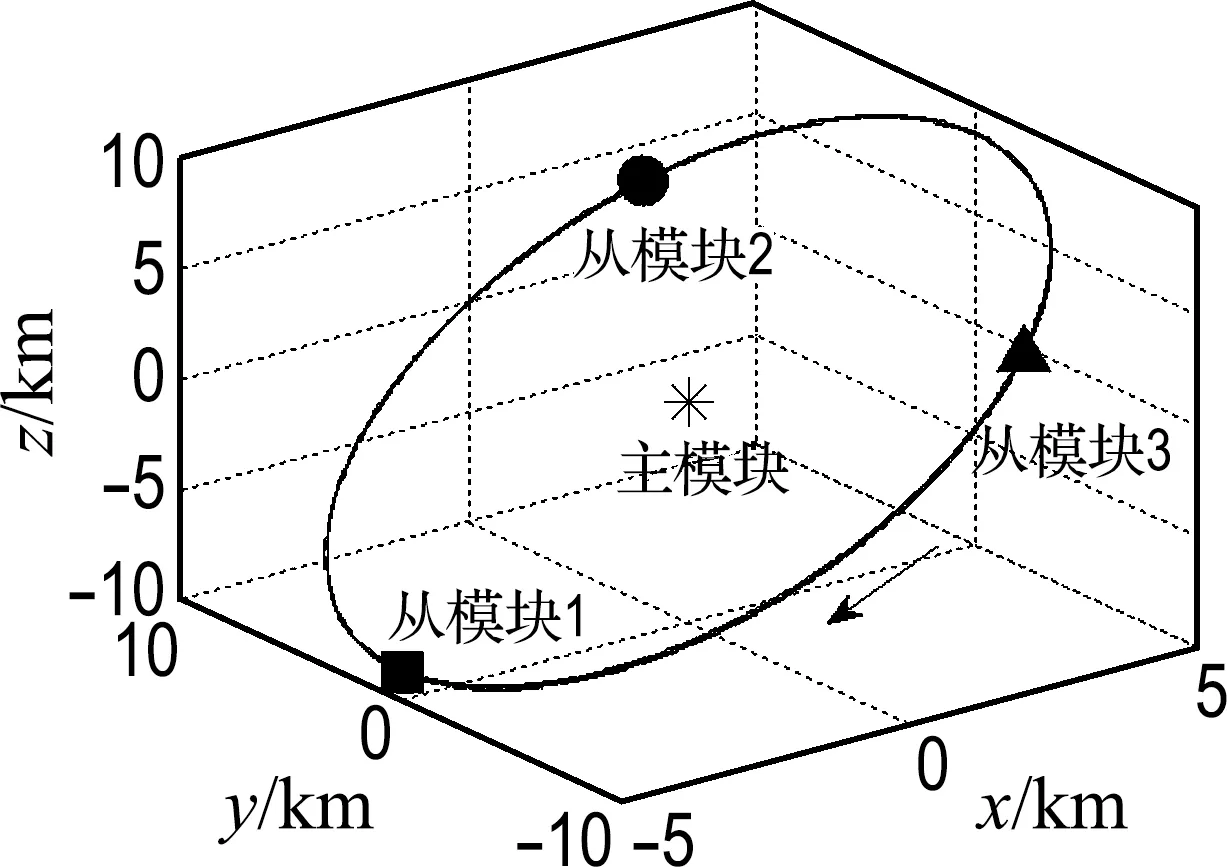
圖2 修正后J2攝動下編隊飛行的三維軌跡

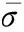
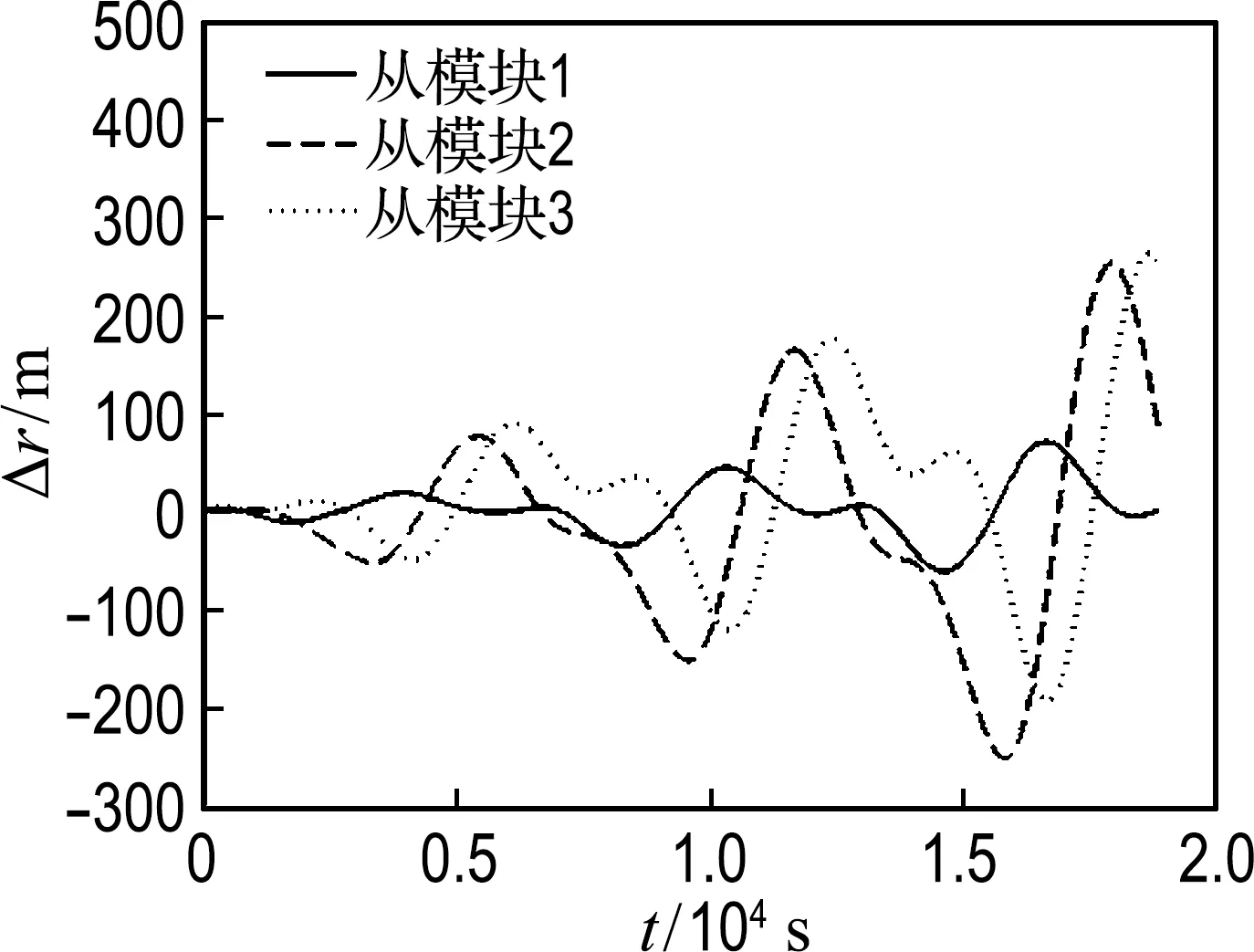
(a) 未修正時

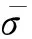
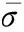
4 結 論

(1)當主模塊位于小偏心率軌道，不考慮J2攝動時，相對運動方程設計結果具有很高的精度，但不適用于赤道軌道和極地軌道的編隊構形設計．

(2)主模塊位于太陽同步軌道，其平均軌道偏心率為0時，無法采用零J2攝動條件進行修正．

(3)本文的修正公式有效抑制了編隊構形的跡向漂移，實際編隊時，從模塊與主模塊的平均軌道傾角之差越小，其相對漂移越小，所以應盡可能設計同軌道傾角編隊．考慮J2攝動時，采用平均軌道要素差對集群航天器進行空間圓形編隊設計，對其后續編隊構形保持、節省燃料和控制律的設計具有重要意義．

[1] Mathieu C, Weigel A L. Assessing the flexibility provided by fractionated spacecraft [C] // Space 2005 Conference. Long Beach:American Institute of Aeronautics and Astronautics, 2005:6700.

[2]胡 敏,曾國強. 集群航天器發展概況[J]. 裝備指揮技術學院學報, 2011, 22(4):61-66.

HU Min, ZENG Guo-qiang. Developments of the fractionated spacecraft [J]. Journal of the Academy of Equipment Command & Technology, 2011, 22(4):61-66. (in Chinese)

[3]楊嘉摨. 航天器軌道動力學與控制(上)[M]. 北京:中國宇航出版社, 2009.

YANG Jia-zhi. Spacecraft Orbit Dynamics and Control:Part 1 [M]. Beijing:China Astronautic Publishing House, 2009. (in Chinese)

[4]高云峰,寶音賀西,李俊峰. 衛星編隊飛行中C-W方程與軌道根數法的比較[J]. 應用數學和力學, 2003, 24(8):799-804.

GAO Yun-feng, BAOYIN He-xi, LI Jun-feng. Comparison of two methods in satellite formation flying [J]. Applied Mathematics and Mechanics, 2003, 24(8):799-804. (in Chinese)

[5]安雪瀅. 橢圓軌道航天器編隊飛行動力學及應用研究[D]. 長沙:國防科學技術大學, 2006.

AN Xue-ying. Dynamics and application of spacecraft formation flying in eccentric orbits [D]. Changsha:National University of Defense Technology, 2006. (in Chinese)

[6]殷建豐,賀 泉,韓 潮. 基于相對軌道要素的航天器相對運動碰撞分析[J]. 航空學報, 2011, 32(2):311-320.

YIN Jian-feng, HE Quan, HAN Chao. Collision analysis of spacecraft relative motion based on relative orbit elements [J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(2):311-320. (in Chinese)

[7]孟 鑫,李俊峰,高云峰. 一種便于攝動分析的編隊飛行衛星相對運動的描述[J]. 應用數學和力學, 2005, 26(11):72-80.

MENG Xin, LI Jun-feng, GAO Yun-feng. Useful relative motion description method for perturbations analysis in satellite formation flying [J]. Applied Mathematics and Mechanics, 2005, 26(11):72-80. (in Chinese)

[8]胡 敏,曾國強. 平均軌道根數與密切軌道根數的互換[J]. 飛行器測控學報, 2012, 31(2):77-81.

HU Min, ZENG Guo-qiang. Transformation between mean and osculating orbital elements [J]. Journal of Spacecraft TT&C Technology, 2012, 31(2):77-81. (in Chinese)

[9]劉 林. 航天器軌道理論[M]. 北京:國防工業出版社, 2000.

LIU Lin. Orbit Theory of Spacecraft [M]. Beijing:National Defense Industry Press, 2000. (in Chinese)

[10]袁建平,和興鎖. 航天器軌道機動動力學[M]. 北京:中國宇航出版社, 2010.

YUAN Jian-ping, HE Xing-suo. Spacecraft Orbital Maneuvering Dynamic [M]. Beijing:China Astronautic Publishing House, 2010. (in Chinese)

[11]曹 靜,袁建平,羅建軍. 一組新的四元數軌道要素建模方法[J]. 中國空間科學技術, 2013(5):62-68.

CAO Jing, YUAN Jian-ping, LUO Jian-jun. A set of novel orbital elements modeling approach using quaternion [J]. Chinese Space Science and Technology, 2013(5):62-68. (in Chinese)

[12]孟 鑫,李俊峰,高云峰. 編隊飛行衛星相對運動的零J2攝動條件[J]. 清華大學學報:自然科學版, 2004, 44(2):219-223.

MENG Xin, LI Jun-feng, GAO Yun-feng. J2 invariant perturbation conditions for the relative movement for satellites in formation flying [J]. Journal of Tsinghua University:Science and Technology, 2004, 44(2):219-223. (in Chinese)

[13]郝繼剛. 分布式衛星編隊構形控制研究[D]. 長沙:國防科學技術大學, 2006.

HAO Ji-gang. Study on formation configuration control of distributed satellites [D]. Changsha:National University of Defense Technology, 2006. (in Chinese)

[14]王 瑞,向開恒,馬興瑞. 平均軌道要素及其在衛星星座設計中的應用[J]. 中國空間科學技術, 2002(5):16-22.

WANG Rui, XIANG Kai-heng, MA Xing-rui. The mean orbit elements and its application in the satellite constellation design [J]. Chinese Space Science and Technology, 2002(5):16-22. (in Chinese)

Space circular formation configuration design of fractionated spacecraft based on difference of mean orbital elements for J2 perturbation

ZHANG Shuo1, WU Guo-qiang*1,2

( 1.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China；2.School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China )

Fractionated spacecraft is a virtual spacecraft system which is constituted by wireless connection. The space circular formation configuration design as the chief module at the sun-synchronous orbit for J2 perturbation, has great significance of meeting the needs of energy transfer and data exchange accurately between the modules, and its application requirements. To begin with, relative motion model is established through the difference of mean orbital elements between deputy module and chief module, and the design steps of the space circular formation configuration are given. The J2 invariant perturbation conditions are no longer applied, so the revised formula is proposed through the quantitative analysis of J2 perturbation. The initial formation configuration is determined by converting the revised mean orbital elements to the osculating orbital elements at the initial time. The nonsingular novel quaternion orbital elements are used to analyze J2 perturbation, and the efficacy of the design method is demonstrated by the results of simulations.

J2 perturbation; mean orbital elements; fractionated spacecraft; space circular formation

1000-8608(2015)03-0236-07

2014-08-10；

2015-01-18．

國家自然科學基金資助項目(11202044).

張 朔(1990-)，男，碩士生，E-mail:dlzs@mail.dlut.edu.cn；吳國強*(1977-)，男，博士，副教授，碩士生導師，E-mail:gqwu@dlut.edu.cn.

V412.4

A

10.7511/dllgxb201503002