離心壓縮機模型級尺寸縮放對性能影響數值研究

劉 艷， 王 海 倫， 王 鍵， 王 學 軍， 汪 創 華

( 1.大連理工大學 能源與動力學院, 遼寧 大連 116024；2.沈陽鼓風機集團股份有限公司， 遼寧 沈陽 110142 )

離心壓縮機模型級尺寸縮放對性能影響數值研究

劉 艷*1， 王 海 倫1， 王 鍵1， 王 學 軍2， 汪 創 華2

( 1.大連理工大學 能源與動力學院, 遼寧 大連 116024；2.沈陽鼓風機集團股份有限公司， 遼寧 沈陽 110142 )

選用流量系數分別為0.015 0、0.033 5、0.068 0和0.120 0的4組離心壓縮機模型級為研究對象,幾何縮放比尺分別選取0.78、1.00、1.89和2.67．采用數值方法對這些模型級進行計算，進而獲得每個模型級的氣動性能．同時,對流量系數為0.033 5和0.068 0兩個模型級的計算結果與實驗值進行對比，對計算精度進行了評價．綜合4組模型級的計算結果，可以發現：幾何相似放大后的模型級由于雷諾數增大，邊界層流動改善，因而其氣動性能比基準級提高了．相反，幾何相似縮小后的模型級由于雷諾數減小，邊界層相對變厚，黏性損失增加，因而其多變效率比大尺寸模型級降低了，但縮放后的模型級能頭系數變化不大． 在研究的流量系數范圍內，流量系數越小，尺寸縮放對多變效率的影響就越顯著．模型級尺寸放大后，其最大效率所對應的流量系數將向增大的方向偏移，比尺越大偏移越大，但偏移量較小．

離心壓縮機；模型級；尺寸效應；湍流模擬；氣動性能

0 引 言

現代離心壓縮機的設計和制造大都根據用戶需求，單件設計和生產．單件設計需要有不同系列的模型級數據庫，設計者根據用戶要求，基于已有的模型級數據庫或模型機，利用相似理論進行方案設計和最終設計．由于完全相似條件很難滿足，按比例放大或縮小的模型級的氣動性能與原型級不完全相同．這其中有幾何結構方面的原因也有流動本身的原因，如表面粗糙度、密封間隙、葉片厚度以及邊界層大小等．因此，經過模化得到的壓縮機的性能與模型級會有一定差別，這種性能差別稱為尺寸效應．尺寸效應的研究對實際產品設計具有重要的指導作用．

陳國福[1]根據國外管線離心壓縮機的雙級模型及實物機器性能實驗結果得出，當葉輪出口直徑大于基準模型級時，其多變效率增加；當葉輪出口直徑小于基準模型級時，其多變效率降低．祁大同等[2]研究了離心壓縮機和通風機葉輪進口密封間隙對性能相似換算的影響，從理論上進行分析并探討了修正方法，結果表明由于密封間隙往往不能按照比例進行縮放，小尺寸模型級的泄漏量相對較大．盧金鈴等[3]定性討論了葉片厚度和流道表面相對粗糙度對離心壓縮機性能相似換算的影響，并結合算例進行了探討和分析，對小尺寸模型級而言,葉片厚度和表面粗糙度均相對較大,導致阻塞和流動損失也較大,效率偏低．Ma等[4]采用CFD方法研究了幾何相似縮放對某小型離心葉輪性能的影響，在絕熱和等溫兩種壁面條件下，大尺寸葉輪的效率均高于小尺寸葉輪．Schleer等[5]研究了離心壓縮機的幾何縮放對其穩定性以及工況范圍的影響，得出不同尺寸模型級的穩定工況范圍并無較大差別．

雷諾數是慣性力和黏性力的比值，常用來衡量黏性力的影響程度．對于離心壓縮機，雷諾數的表達式有多種，其中特征速度可取相對速度或者葉輪出口周向速度．有關雷諾數對壓縮機性能的影響可參見文獻[6-14]，其中文獻[6-11]給出了效率、壓比等性能參數隨雷諾數變化的預測和修正關系，文獻[12-14]則研究了高空下低雷諾數條件對離心壓氣機性能的影響．本文選取葉輪出口周向速度u2和出口寬度b2為特征參數來定義雷諾數，即Re=u2b2/ν，ν為模型級入口空氣運動黏度．由此可知：在u2一定的情況下，b2越大，雷諾數越高．大流量系數模型級的b2比小流量系數的大，此外，尺寸放大后b2也增大．雷諾數越高，黏性力的影響相對就越小．

已有的研究表明，離心壓縮機結構放大后，氣動性能有所提高，反之亦然．但目前為止，還沒有看到針對不同流量系數壓縮機尺寸效應的綜合研究．基于此，本文對4種流量系數的基準模型級進行尺寸效應研究,對各模型級進行流場計算和分析，進而獲得離心壓縮機模型級尺寸縮放對性能影響的變化規律，為產品模化設計提供理論指導．

1 研究對象

本文選取設計流量系數分別為0.015 0、0.033 5、0.068 0和0.120 0的4個離心壓縮機模型級作為研究對象，為方便說明，依次記為Model1、Model2、Model3和Model4．4個模型級均由葉輪、無葉擴壓器、彎道和回流器組成．Model1和Model2的葉輪為二元結構，Model3和Model4的葉輪為三元結構，各模型級的主要結構參數見表1．基準模型級葉輪出口直徑D2=450 mm，在基準模型級的基礎上，本文選取4個比尺S分別為0.78、1.00、1.89和2.67進行幾何縮小和放大，相應地葉輪出口直徑D2為350、450、850和1 200 mm．

本文根據機器馬赫數相等的原則計算尺寸縮放后新模型級的葉輪轉速，再依據流量系數相等得到尺寸縮放后新模型級的設計流量，換算后的相關參數和雷諾數見表2，工質為空氣．這樣，在保證幾何相似的基礎上，可以滿足進口速度三角形相似、機器馬赫數相等以及絕熱指數相等，理論上滿足了不同尺寸模型級相似的條件[15]．

表1 模型級主要結構參數Tab.1 Main geometrical parameters of model stages

表2 相似換算后各模型級主要參數Tab.2 Operational parameters of model stages after transformation of similarity

2 數值模擬方法

本文使用NUMECA商用軟件包Fine/Turbo 進行定常數值模擬，計算求解圓柱坐標系下三維雷諾平均N-S方程．計算中選用Spallart-Allmaras方程湍流模型，空間項使用二階精度的中心差分格式[16]．為了加快收斂速度,采用了隱式殘差光順和當地時間步長以及完全多重網格技術．

采用NUMECA軟件自帶模塊IGG對計算域進行單通道結構化離散，計算域通道兩側邊界網格設置周期性邊界條件，子午面網格如圖1所示．網格第一層厚度均設為0.005 mm，確保絕大部分壁面第一層網格Y+小于2．動靜子交界處(R-S)使用周向守恒型連接面，數據傳遞采用混合平面法實現，并對動靜交界面上、下游的網格進行了適當的加密，防止交界面前后網格尺寸差異過大，造成不必要的插值誤差．對于幾何縮放后的不同模型級，使用與基準模型級相同的拓撲結構生成網格，R-S線都放置在葉輪出口1.05%D2的位置，以求最大限度地減少網格結構對計算結果的影響．

圖1 子午面網格示意圖Fig.1 Meridional view of grid

使用面積定義法設置葉輪中旋轉的固壁，所有的固壁均采用絕熱、無滑移的邊界條件．計算域入口處給定總溫(293 K)、總壓(98 000 Pa)，軸向進氣，出口給定質量流量．所有工況點經過3 000步以上的迭代均可使計算殘差下降到10-3量級以下，當進出口質量流量誤差小于0.5%，效率和壓比保持恒定時，即可認為計算收斂．

本文以Model 3為例，對葉輪出口直徑D2=850 mm的模型級進行了網格無關性分析，計算結果如圖2所示．由圖2可以看出，當網格節點數大于220×104后，多變效率ηp與滯止壓比ε變化不明顯，可以認為網格達到了無關性．為了節省計算時間，其他不同尺寸模型級的網格數將根據此計算結果進行適當的增減．

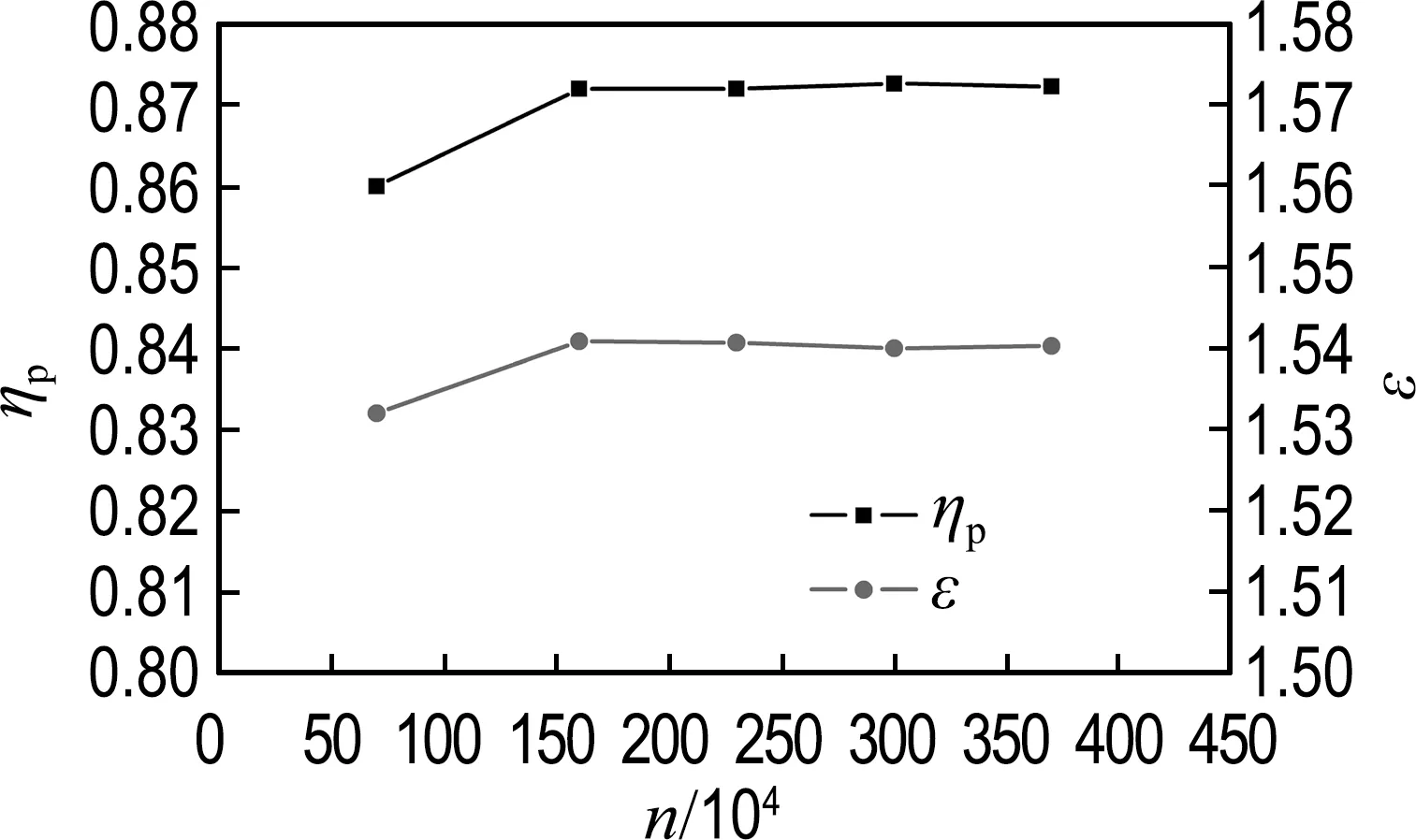
圖2 網格無關性驗證Fig.2 Verification of grid independence

3 計算結果與分析

3.1 模型級數值模擬精度驗證

為了評價數值模擬的可靠性和準確度，本文首先對Model 2(D2=450 mm)和Model 3(D2=850 mm)兩個模型級的計算值與實驗值進行比較．圖3(a)、(b)分別顯示的是兩個模型級的多變效率和能頭系數隨流量系數(φ1)的變化曲線.由圖可以看出，除了最小流量點和最大流量點外，Model 2的多變效率和能頭系數隨φ1的變化趨勢與實驗值吻合很好．在小流量系數φ1=0.024 8 時，計算結果顯示此流量下，壓縮機還沒有發生喘振的特征，而實驗結果卻表明壓縮機有喘振的征兆，因為此流量下，效率明顯下降．Model 3與Model 2相似，設計點附近的計算值與實驗值吻合很好，但計算得到的喘振點和阻塞點所對應的流量系數與實驗值相比偏大．正如文獻[17]中所指出的那樣，遠離設計工況時，氣流沖角發生較大變化，特別是小流量工況，流動還會出現分離，流動變得不穩定．這種情況下，定常計算不太合適，計算誤差較大．本文喘振和阻塞工況不作為重點研究對象，所以沒有采用非定常計算．

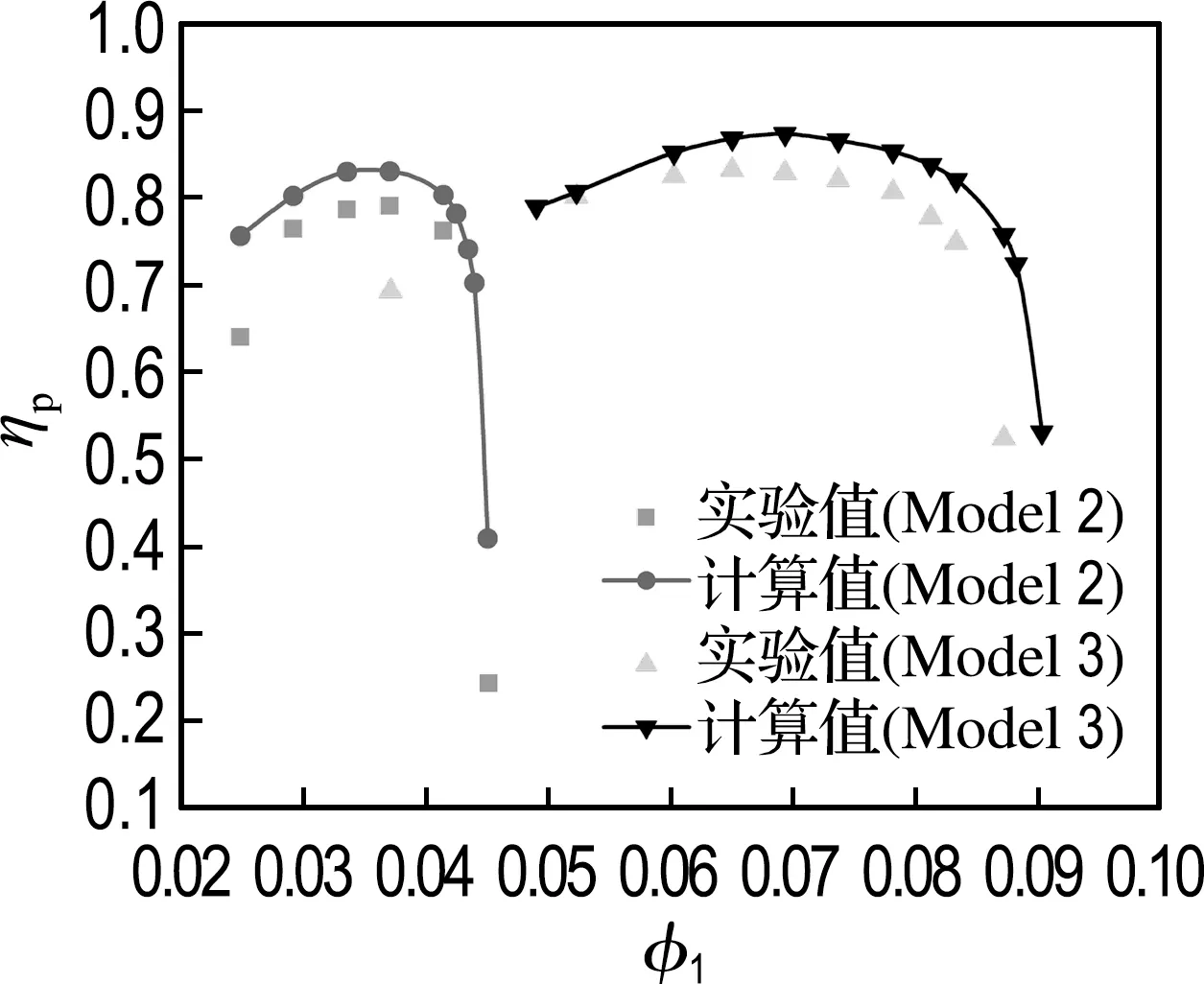
(a) 多變效率曲線

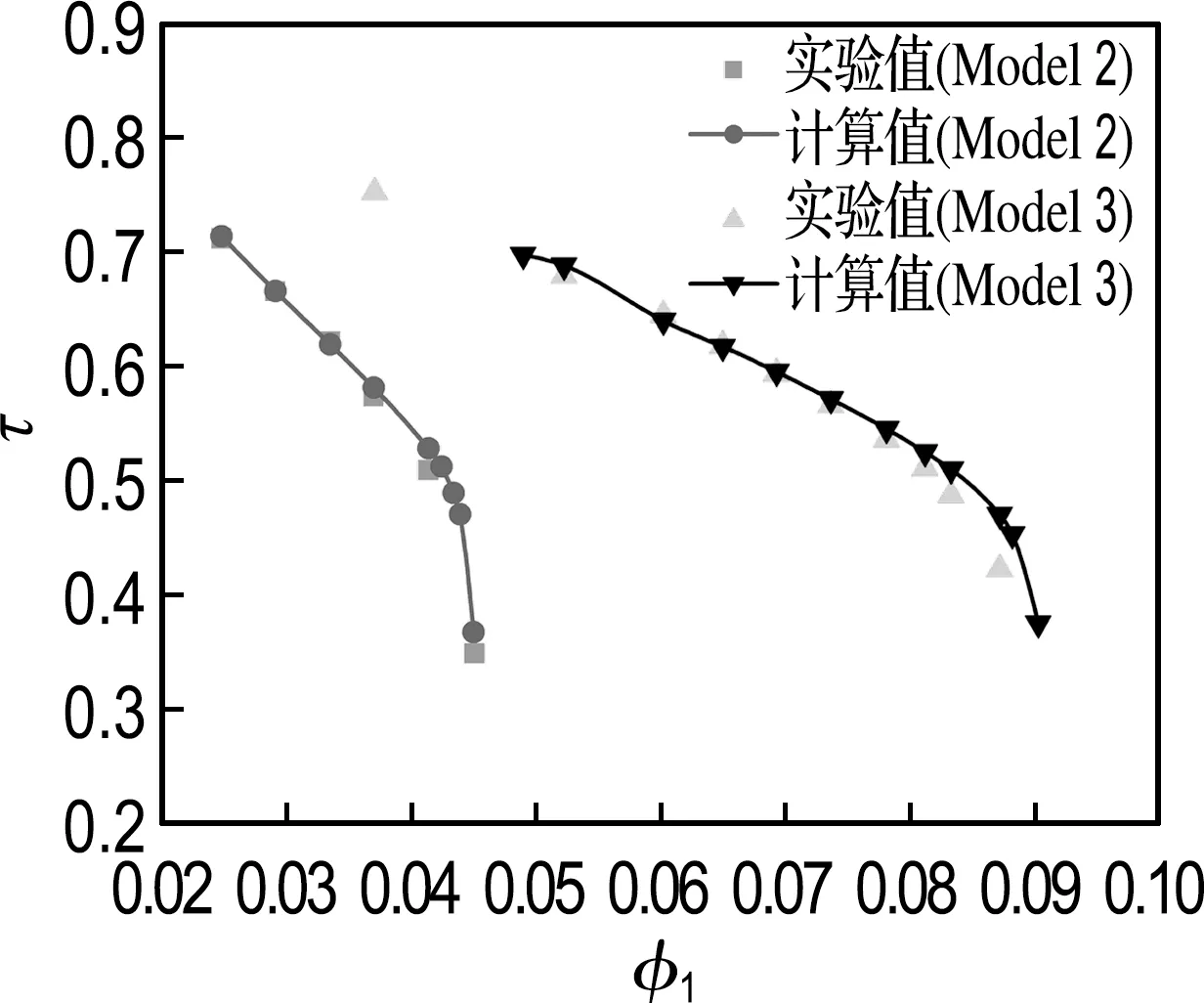
(b) 能頭系數曲線

圖3 Model 2、3計算值與實驗值比較

Fig.3 Comparison of calculated value with measurements for Model 2, 3

綜合Model 2和Model 3的計算結果，可以得出：在忽略密封間隙泄漏影響的情況下，與實驗值相比，設計工況附近兩個模型級平均的多變效率和能頭系數的相對誤差分別約為5.0%和1.8%，且多變效率和能頭系數的變化規律與實驗值吻合較好，說明計算是可靠和可信的，為后續計算提供了支撐．

3.2 模型級尺寸縮放計算結果

3.2.1 氣動性能比較 對每個基準模型級進行尺寸縮小和放大，葉輪出口直徑D2分別為350、450、850、1 200 mm．圖4～7分別顯示的是Model 1～4不同尺寸模型級多變效率和能頭系數曲線．由圖4～7可以清楚地看出，模型放大后，多變效率曲線整體上移，上移幅度因放大比尺的不同而不同，能頭系數不如多變效率隨比尺變化那樣明顯．為進一步研究比尺的影響，考查設計工況點的尺寸效應．

圖8給出了Model 1～4設計工況點的尺寸效應．圖中縱坐標是不同比尺時的多變效率或能頭系數與D2=450 mm模型級的比值．由圖可以看出，4個模型級的多變效率均隨著尺寸的增大而增大．當D2由450 mm增大到850 mm(比尺為1.89)時，Model 1～4的多變效率分別提高了3.20%、1.45%、1.18%和0.60%．當D2由450 mm 增大到1 200 mm(比尺為2.67)時，Model 1～4的多變效率分別提高了5.29%、3.07%、2.33%和1.40%．當D2由450 mm減小到350 mm(比尺為0.78)時，Model 1～4的多變效率分別降低了2.40%、0.84%、0.13%和0.35%．對于能頭系數，除了Model 1(D2=350 mm)的情況，其他模型級隨尺寸的增大并沒有明顯變化．

由圖8(a)還可以看出，在本文研究的流量系數范圍內，流量系數越小，尺寸縮放對多變效率的影響越明顯．這主要是由于小流量系數模型級的雷諾數一般較小(b2較小)，黏性摩擦損失的影響較大，自動模化程度降低，所以尺寸縮放后氣動性能的變化比較明顯．

圖9顯示的是Model 1～4各自幾何相似模型級最大多變效率所對應的流量系數偏移圖，最大值點通過三次樣條插值得到．整體上看，尺寸增大后，最大多變效率也增大，最大值點向流量增大的方向偏移，但流量系數偏移量不大．

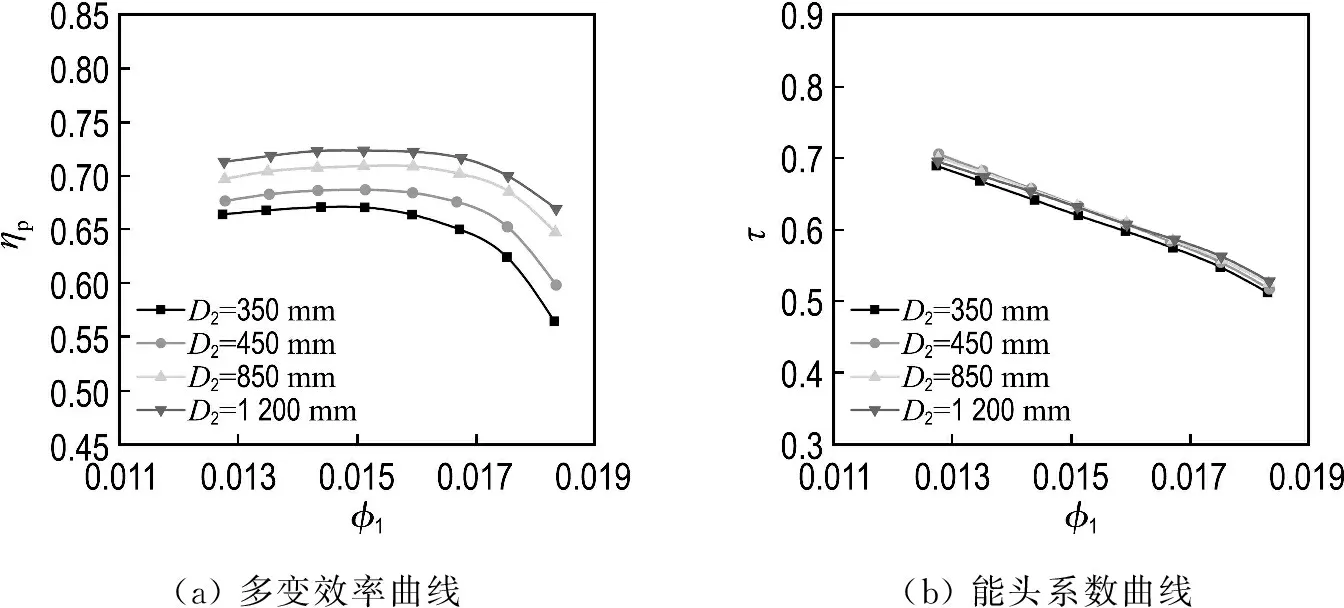
圖4 Model 1不同尺寸模型級多變效率曲線和能頭系數曲線Fig.4 Polytropic efficiency and head coefficient curves of model stages with Model 1 at different sizes

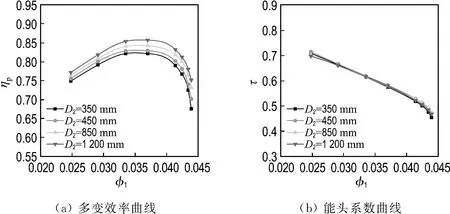
圖5 Model 2不同尺寸模型級多變效率曲線和能頭系數曲線Fig.5 Polytropic efficiency and head coefficient curves of model stages with Model 2 at different sizes

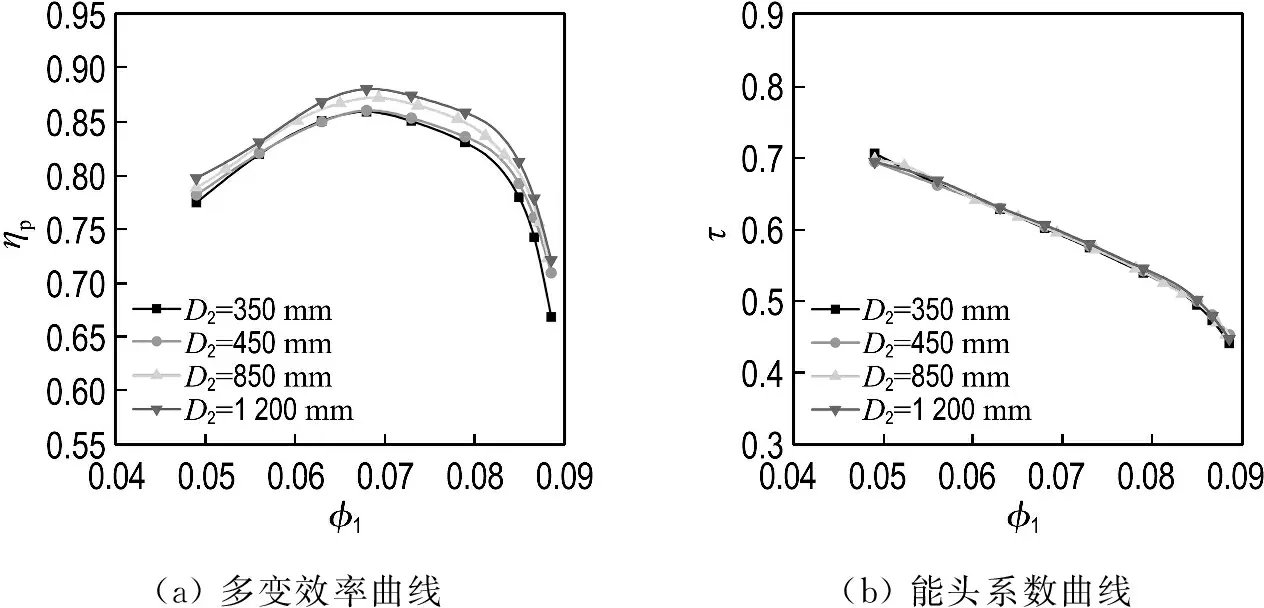
圖6 Model 3不同尺寸模型級多變效率曲線和能頭系數曲線Fig.6 Polytropic efficiency and head coefficient curves of model stages with Model 3 at different sizes

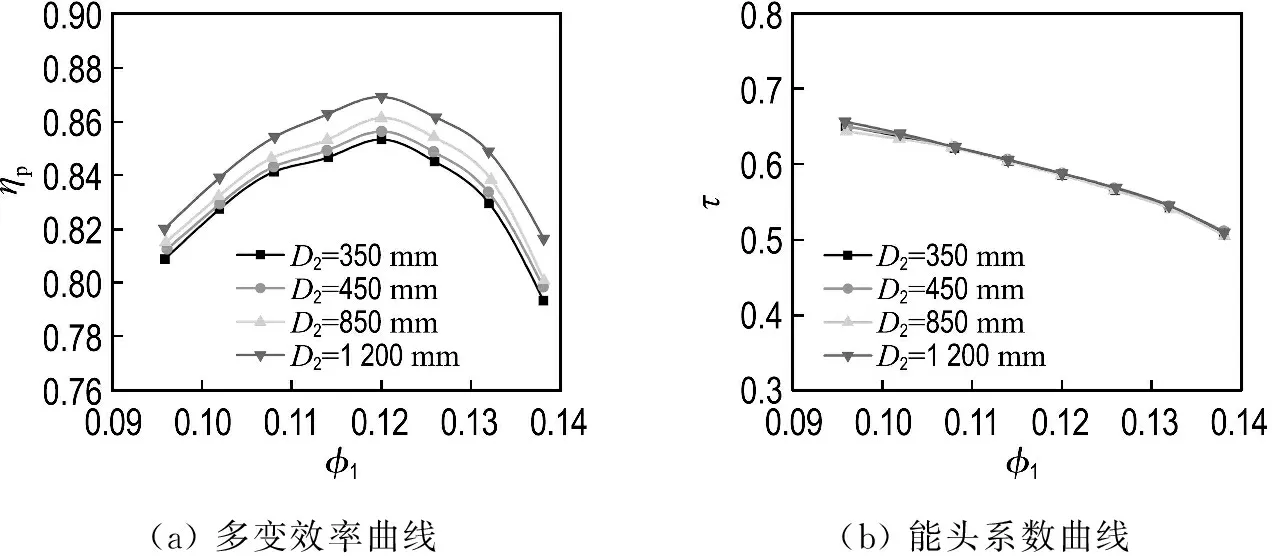
圖7 Model 4不同尺寸模型級多變效率曲線和能頭系數曲線Fig.7 Polytropic efficiency and head coefficient curves of model stages with Model 4 at different sizes

圖8 4個模型級設計工況點的尺寸效應

Fig.8 Size effects of the four models at the design condition point

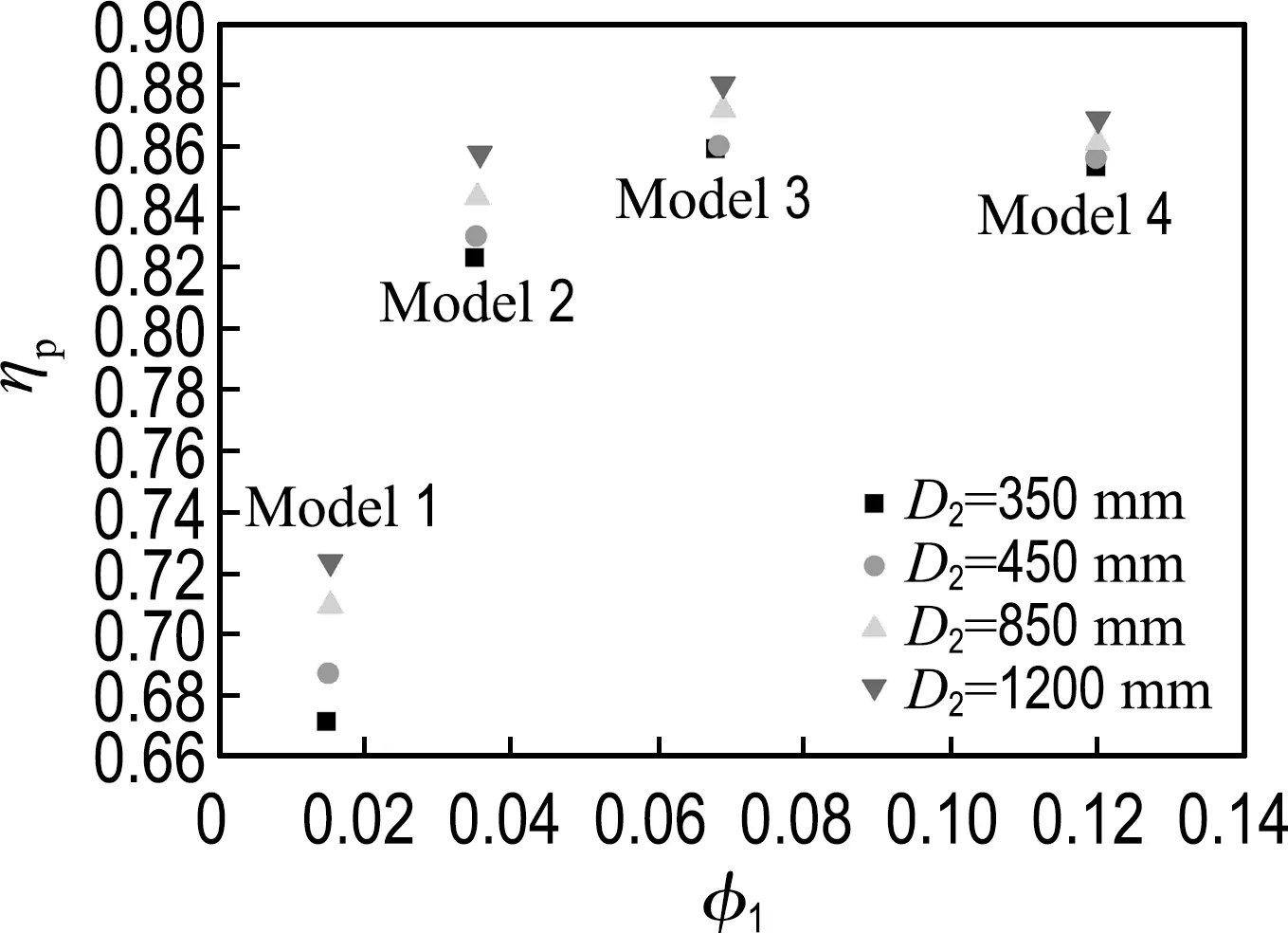
圖9 流量系數偏移圖Fig.9 Shift map of flow coefficient

3.2.2 流場分析 為了從物理上說明尺寸放大后性能提高的原因，需要研究流場參數的變化．在本文計算中，壁面按光滑壁面處理，因而沒有考慮粗糙度變化的影響．經流場分析可知，在Model 1～4整個通道內都沒有產生明顯的漩渦和回流，且4組模型級在不同尺寸下各參數的分布規律很相似，所以下文將以Model 3為例，對不同尺寸設計工況下的流場進行對比和分析．

周向平均的子午流線如圖10所示，可以看出4個尺寸下的流線分布很相近．為了進一步分析不同尺寸下氣動性能的微小差異，需要比較熵的分布[18]．葉輪50%葉高截面處的熵分布如圖11所示，4個尺寸下流場的分布規律相似，熵值較大的區域均集中在葉輪出口吸力面附近．一方面由于葉輪通道是擴壓通道，邊界層沿通道不斷增厚；另一方面由于二次流的存在，低速氣流不斷從壓力面涌向吸力面，使吸力面的邊界層增厚，流動情況惡化，以致形成了高熵區．由圖11可以明顯看出，大尺寸模型級高熵值的區域比較小，損失少，氣動性能較好；而小尺寸模型級近壁面處熵增較大，氣動性能比大尺寸模型級降低了．正如前面所述，在葉輪出口圓周速度相同的條件下，尺寸增大，雷諾數也增大，邊界層相對變薄，黏性的影響相對減弱，因此高熵值的區域減小，氣動性能變好；而幾何相似縮小后的模型級由于雷諾數減小，邊界層相對變厚，近壁面處的流動更易分離，增加了黏性損失，因而在近壁面處熵增較大，氣動性能降低了．

回流器50%葉高截面處的熵分布如圖12所示．回流器具有通道狹長、工質流速低的特點，葉片表面邊界層比較厚，使得摩擦損失較大．尤其在吸力面后半段，4個模型級均存在一個熵值較大的區域，且模型級尺寸越小，此區域的面積越大，這主要是由于葉根、葉尖兩個端壁二次流的遷移與堆積造成的[19]．隨著尺寸的減小，雷諾數減小，黏性的作用增強，導致摻混損失增大．

圖10 周向平均的子午流線Fig.10 Circumferentially averaged meridional streamline

圖11 葉輪50%葉高截面熵分布Fig.11 Entropy distribution of impeller at 50% spanwise section

圖12 回流器50%葉高截面熵分布

Fig.12 Entropy distribution of return at 50% spanwise section

圖13顯示的是葉輪出口(1.022%D2處)截面各周向平均參數沿葉輪出口量綱一化寬度變化曲線．需要說明的是，橫坐標(0)點對應的是盤側，橫坐標(1.0)點對應的是蓋側．總壓比定義為各點當地總壓與入口總壓(98 000 Pa)的比值．由圖13可以清楚地看出，4個尺寸下各參數的分布規律很相似．在邊界層之外的主流區域，多變效率呈現出從輪盤到輪蓋逐漸下降的趨勢，總溫和子午速度沿展向均先減小再增大，且不同尺寸下極值點的位置趨于一致；總壓比則隨著尺寸的放大而增大．從圖13(a)壁面(盤側)附近的局部放大圖中可以清楚地看出，由于小尺寸模型級邊界層相對較厚，靠近壁面處尺寸大的模型級子午速度要大一些，遠離壁面進入主流區后，尺寸小的模型級子午速度要大一些，符合邊界層內速度分布規律；從圖13(b)也可以得到，靠近壁面處，大尺寸模型級的多變效率要高于小尺寸，說明大尺寸模型級邊界層內的流動改善了，因而效率提高了．其他截面位置的參數分布與圖13相似，不再重復顯示．

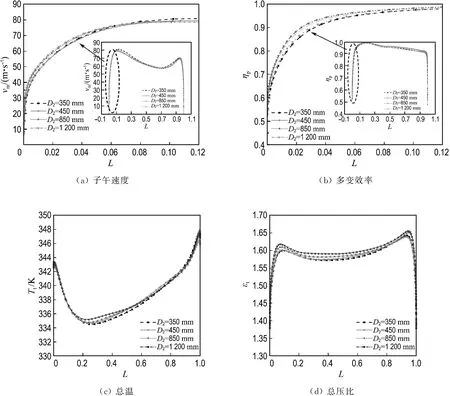
圖13 周向平均參數沿葉輪出口寬度的變化曲線

Fig.13 Variation curves of circumferentially averaged parameters along the width of impeller outlet

4 結 論

(1)除近失速和喘振工況以及近阻塞工況外，定常計算得到的流量系數為0.033 5和0.068 0兩個模型級的氣動性能規律與實驗吻合較好，平均多變效率和能頭系數的相對誤差分別約為5.0% 和1.8%，說明設計工況附近流動不穩定程度不大，定常計算是可信和可靠的．

(2)在不考慮制造誤差的影響時，幾何相似放大后的模型級由于雷諾數增大，邊界層流動改善，因而其氣動性能比基準模型級提高了．相反，縮小后的模型級由于雷諾數減小，邊界層相對變厚，近壁面處的流動更易分離，增加了黏性損失，因而多變效率比大尺寸模型級降低了，但能頭系數變化不大．

(3)在本文研究的流量系數范圍內，流量系數越小，尺寸縮放對多變效率的影響就越明顯．這主要是由于大流量系數模型級的雷諾數一般較高，使得黏性摩擦損失的影響變小，自動模化的程度提高，所以尺寸縮放后氣動性能的變化就不明顯了．在設計中可以進行相應的氣動性能修正．

(4)模型級尺寸放大后，其最大效率所對應流量系數將向增大的方向偏移，但偏移量較小．

(5)本文所研究的4個離心壓縮機模型級都沒有葉片擴壓器，且計算中并沒有考慮制造誤差以及間隙泄漏，所得結論具有一定的局限性．今后還要對微小以及特大流量系數模型級的尺寸效應進行研究，同時要增大縮放的比尺，從而找到更加普遍的規律．

[1] 陳國福. 離心壓縮機的比例尺寸對性能的影響研究[J]. 化工與通用機械, 1982(4):6-12.

CHEN Guo-fu. Study of scale effects on performance of centrifugal compressors [J]. Chemical and General Machinery, 1982(4):6-12. (in Chinese)

[2]祁大同,李占良,袁民健,等. 葉輪進口密封間隙對離心式壓縮機、通風機性能相似換算的影響[J]. 流體機械, 1991(10):30-33.

QI Da-tong, LI Zhan-liang, YUAN Min-jian,etal. The influence of sealing clearance at inlet of impeller for transformation of similitude on performance of centrifugal compressors and fans [J]. Fluid Machinery, 1991(10):30-33. (in Chinese)

[3]盧金鈴,祁大同,李景銀,等. 離心壓縮機性能相似換算的修正計算[J]. 流體機械, 1999, 27(3):18-22.

LU Jin-ling, QI Da-tong, LI Jing-yin,etal. A correction method for transformation of similitude on performance of centrifugal compressors [J]. Fluid Machinery, 1999, 27(3):18-22. (in Chinese)

[4]MA Yan, XI Guang. Effects of Reynolds number and heat transfer on scaling of a centrifugal compressor impeller [C] // ASME Turbo Expo 2010:Power for Land, Sea, and Air, GT 2010. New York:American Society of Mechanical Engineers, 2010:565-572.

[5]Schleer M, Abhari R S. Influence of geometric scaling on the stability and range of a turbocharger centrifugal compressor [C] // ASME Turbo Expo 2005, GT-2005-68713. New York:ASME, 2005.

[6]Bullock R O. Analysis of Reynolds number and scale effects on performance of turbomachinery [J]. Journal of Engineering for Power, 1964, 86(3):247-256.

[7]Pelz P F, Stonjek S S. The influence of Reynolds number and roughness on the efficiency of axial and centrifugal fans — a physically based scaling method [J]. Journal of Engineering for Gas Turbines and Power, 2013, 135(5):052601.

[8]Simon H, Bülsk?mper A. On the evaluation of Reynolds number and relative surface roughness effects on centrifugal compressor performance based on systematic experimental investigations [J]. Journal of Engineering for Gas Turbines and Power, 1984, 106(2):489-498.

[9]Casey M V. The effects of Reynolds number on the efficiency of centrifugal compressor stages [J]. Journal of Engineering for Gas Turbines and Power, 1985, 107(2):541-548.

[10]Casey M V, Robinson C J. A unified correction method for Reynolds number, size, and roughness effects on the performance of compressors [J]. Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy, 2011, 225(7):864-876.

[11]Strub R A, Bonciani L, Borer C J,etal. Influence of the Reynolds number on the performance of centrifugal compressors [J]. Journal of Turbomachinery, 1987, 109(4):541-544.

[12]陳 浮,王云飛,陳煥龍,等. 雷諾數對帶蝸殼的離心壓氣機內部流場影響研究[J]. 推進技術, 2013, 34(7):911-917.

CHEN Fu, WANG Yun-fei, CHEN Huan-long,etal. Effects of Reynolds number on internal flow field of centrifugal compressor with the volute [J]. Journal of Propulsion Technology, 2013, 34(7):911-917. (in Chinese)

[13]曾令君,馬千里. 雷諾數對壓氣機性能影響的數值模擬[J]. 汽輪機技術, 2008, 50(5):325-330.

ZENG Ling-jun, MA Qian-li. The simulation of the Reynolds number effects on the characteristic of the compressor [J]. Turbine Technology, 2008, 50(5):325-330. (in Chinese)

[14]霍 磊,劉火星. 低雷諾數下離心壓氣機性能及流動影響的數值研究[J]. 航空動力學報, 2013, 28(4):911-920.

HUO Lei, LIU Huo-xing. Numerical analysis of centrifugal compressor performance and flow at low Reynolds number [J]. Journal of Aerospace Power, 2013, 28(4):911-920. (in Chinese)

[15]徐 忠. 離心式壓縮機原理[M]. 北京:機械工業出版社, 1990.

XU Zhong. Principle of Centrifugal Compressors [M]. Beijing:China Machine Press, 1990. (in Chinese)

[16]王福軍. 計算流體動力學分析[M]. 北京:清華大學出版社, 2004.

WANG Fu-jun. Analysis of Computational Fluid Dynamics [M]. Beijing:Tsinghua University Press, 2004. (in Chinese)

[17]孔祥杰,劉正先,郭 佳. 計算軟件對離心壓縮機性能的數值模擬及與試驗結果的對比驗證[J]. 風機技術, 2008(2):48-50.

KONG Xiang-jie, LIU Zheng-xian, GUO Jia. Numerical simulation for centrifugal compressor performance based on CFD software and the comparison with test result [J]. Compressor Blower & Fan Technology, 2008(2):48-50. (in Chinese)

[18]沈維道,童鈞耕. 工程熱力學[M]. 北京:高等教育出版社, 2007.

SHEN Wei-dao, TONG Jun-geng. Engineering Thermodynamics [M]. Beijing:Higher Education Press, 2007. (in Chinese)

[19]高 星,劉寶杰. 雙級離心壓氣機回流器流動特點分析[J]. 航空動力學報, 2009, 24(2):432-438.

GAO Xing, LIU Bao-jie. Analysis of the flow in return vanes of a two-stage centrifugal compressor [J]. Journal of Aerospace Power, 2009, 24(2):432-438. (in Chinese)

Numerical study of scale effects on performance of centrifugal compressor model stage

LIU Yan*1, WANG Hai-lun1, WANG Jian1, WANG Xue-jun2, WANG Chuang-hua2

( 1.School of Energy and Power Engineering, Dalian University of Technology, Dalian 116024, China；2.Shenyang Blower Works Group Corporation, Shenyang 110142, China )

Four groups of centrifugal compressor model stages are chosen with flow coefficients of 0.015 0, 0.033 5, 0.068 0 and 0.120 0. Scales of 0.78, 1.00, 1.89 and 2.67 are set. Numerical methods are applied in order to investigate aerodynamic performance of each model stage. Meanwhile, calculation results for two model stages with flow coefficients of 0.033 5 and 0.068 0 are compared with experimental data, and the calculation accuracy is evaluated. Synthesizing calculation results of these four groups of model stages, it can be found that aerodynamic performance of geometric similarity enlarged model stages is improved due to the increase in Reynolds number and improvement of flow in boundary layers. In contrast, the polytropic efficiency of geometric similarity shrunken model stages declines due to the increase in thickness of boundary layers and in viscous loss caused by the decrease of Reynolds number. However, head coefficients do not change much for these scaled model stages. Within the range of flow coefficients studied, the smaller the flow coefficient is, the more significant the scale effect on polytropic efficiency is. The flow coefficients corresponding to the maximum polytropic efficiency make a shift to the direction of increase. The larger the scale is, the larger the displacement is, but the shift is relatively small.

centrifugal compressor; model stage; scale effect; turbulent simulation; aerodynamic performance

1000-8608(2015)03-0252-09

2014-11-27；

2014-12-19．

遼寧省自然科學基金資助項目(2014010502-301)；中央高校基本科研業務費專項資金資助項目(DUT14ZD204，DUT14LH007).

劉 艷*(1966- )，女，博士，教授，E-mail:yanliu@dlut.edu.cn.

TH452

A

10.7511/dllgxb201503004