THE INVARIANCE OF STRONG AND ALMOSTSPIRALLIKE MAPPINGS OF TYPE β AND ORDER α?
(崔艷艷)(王朝君)
College of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001,China
E-mail:cui9907081@163.com;wang9907081@163.com
Hao LIU(劉浩)
College of Mathematics and Information Science,Henan University,Kaifeng 475001,China
E-mail:haoliu@henu.edu.cn
THE INVARIANCE OF STRONG AND ALMOST
SPIRALLIKE MAPPINGS OF TYPE β AND ORDER α?
Yanyan CUI(崔艷艷)?Chaojun WANG(王朝君)
College of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001,China
E-mail:cui9907081@163.com;wang9907081@163.com
Hao LIU(劉浩)
College of Mathematics and Information Science,Henan University,Kaifeng 475001,China
E-mail:haoliu@henu.edu.cn
The invariance of strong and almost spirallike mappings of type β and order α is discussed in this paper.From the maximum modulus principle of holomorphic functions,we obtain that the generalized Roper-Sufridge operators preserve strong and almost spirallikeness of type β and order α on the unit ball Bnin Cnand on bounded and complete Reinhardt domains.Therefore we obtain that the generalized Roper-Sufridge operators preserve strong spirallikeness of type β,strong and almost starlikeness of order α,strong starlikeness on the corresponding domains.Thus we can construct more subclasses of spirallike mappings in several complex variables.
strong and almost spirallike mappings of type β and order α;Roper-Sufridge operators;homogeneous expansion
2010 MR Subject Classifcation32A30;30C25
1 Introduction
As we all know,there are a lot of beautiful results in one complex variable.In the progress of generalizing these results in several complex variables,some basic conclusions(e.g.the models of the coefcients of the homogeneous expansion of an univalent analytic function on the unit disk are bounded)don’t hold in several complex variables.So many people began to discuss the mappings whose image regions have particular geometric properties,such as starlike mappings, convex mappings[1-7].So starlike mappings and convex mappings play an important role in several complex variables.Later many scholars discussed the subclasses or expansions of the two classes in the geometric function theories of several complex variables[8-12].At that time, people knew few examples of normalized biholomorphic starlike mappinngs,convex mapping and their subclasses or expansions.While such examples are lots of in one complex variable.So many people began to construct the corresponding mappings on specifc domains in several complex variables from normalized biholomorphic starlike functions,convex functions and their subclasses or expansions.
In the following,let D be the unit disk in C.Let Bnbe the unit ball in Cn.
In 1995,Roper and Sufridge[13]introduced an operator

In 2005,Muir and Sufridge[18]introduced a generallized Roper-Sufridge operator

Wang and Liu[19]generallized the above operator as follows
They discussed that the generallized Roper-Sufridge operator preserves almost starlikeness of order α and starlikeness of order α if‖P‖satisfes diferent conditions.
In this paper,the above operators are generalized further.We discuss the generallized Roper-Sufridge operators preserve the properties of the subclasses of biholomorphic mappings.
In 1995,Chuaqui[20]introduced the defnition of strong and almost starlike mappings of order α on Bnfrstly.In 2010,Liu[21]generalized the defnition on bounded starlike and circular domains and on the unit ball in complex Banach spaces.They established the relation between the class of almost starlike mappings of order α and the class of strong and almost starlike mappings of order α.
In 2001,Hamada and Kohr[22]introduced the defnition of strong spirallike mappings of type β.Xu and Liu[23]generalized the defnition on the unit ball in complex Banach spaces and they obtained the growth and covering theorems for the mappings.In 2010,Xu and Liu [24]introduced the defnition of strong and almost spirallike functions of type β and order α by combining strong and almost starlike mappings of order α and strong spirallike mappings of type β.
In this paper,we generalize the defnition of strong and almost spirallike functions of type β and order α on Bnand bounded Reinhardt domains.We discuss the invariance of strong and almost spirallike mappings of type β and order α under some generalized Roper-Sufridge operators.

Then we say that f(z)is a strong and almost spirallike functions of type β and order α on D.
If we generalize Defnition 1.1 on the unit ball Bnin Cnand on bounded Reinhardt domains, we obtain the following defnitions.

Then we say that f(z)is a strong and almost spirallike functions of type β and order α on Bn.
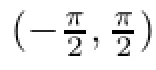
Then we say that f(z)is a strong and almost spirallike functions of type β and order α on Ω.
Remark 1.4Let α=0,β=0,α=β=0 in the above defnitions respectively,we obtain the corresponding defnitions of strong spirallike mappings of type β,strong and almost starlike mappings of order α,strong starlike mappings.
In order to give the main results,we need the following lemmas.
Lemma 1.5(see[25])Let f(z)be an univalent analytic function on D,|f(z)|<1.Then
Lemma 1.6(see[25])Let f(z):D→D be an analytic function on D and f(0)=0. Then|f′(0)|≤1 and|f(z)|≤|z|for?z∈D.
2 Main Results
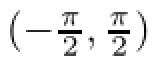
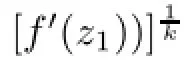
F(z)is a strong and almost spirallike functions of type β and order α on Bn.
ProofFrom Defnition 1.2,we need only to prove

by direct computations,we get
Letting ν(z)=(DF(z))-1F(z)=(a,A)′,where A∈Cn-1,we have
As?P(z0)z0=kP(z0),we can get
For(DF(z))-1F(z)=ν(z)=(a,A)′,we obtain
Since f(z)is a strong and almost spirallike functions of type β and order α on D,we have |λ(z1)|<1.By direct computations,we get
It follows that
From(2.2)and(2.3),we obtain
On the one hand,we have
we obtain
On the other hand,from Lemma 1.5,we have
Thus
As
Therefore
From(2.4),(2.5)and(2.6),we obtain
It follows that F(z)is a strong and almost spirallike functions of type β and order α on Bn. ?


F(z)is a strong and almost spirallike functions of type β and order α on Bn.
ProofFrom Defnition 1.2,we only need to prove

Since f(z)is a strong and almost spirallike functions of type β and order α on D,from Defnition 1.1,we have
For
by direct computations,we get
Lettingμ(z)=(DF(z))-1F(z)=(b,B)′,where B∈Cn-1,we get DF(z)μ(z)=F(z)which follows that
As?P(z0)z0=kP(z0),by direct computations,we can get
For(DF(z))-1F(z)=μ(z)=(b,B)′,we obtain
So
On the other hand,we can get
Letting

As
For f′(z1)/=0,we get g(z1)is holomorphic on D.From Lemma 1.6,we have|g(z1)|≤|z1|,i.e.,
If
from(2.9)and(2.10),we can get
From(2.7),(2.8)and(2.11),we obtain
It follows that F(z)is a strong and almost spirallike functions of type β and order α on Bn. ?
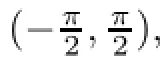

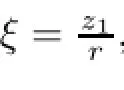
where
Thus
Therefore
So we get
Letting
It follows that F(z)is a strong and almost spirallike functions of type β and order α on Ω.?
Remark 2.4Letting α=0,β=0,α=β=0 in Theorems 2.1-2.3,we obtain the corresponding conclusions of strong spirallike mappings of type β,strong and almost starlike mappings of order α,strong starlike mappings,respectively.

[2]Barnard R W,FitzGerald C H,Gong S.The growth and -theorem for starlike mappings in Cn.Pacifc J Math,1991,150:13-22
[3]Hamada H.starlike mappings on bounded balanced domains with C1-plurisubharmonic defning functions. Pacifc J Math,2000,194(2):359-371
[4]Hamada H,Honda T.Sharp growth theorems and coefcient bounds for starlike mappings in several complex variables.Chin Ann Math,2008,29B(4):353-368
[5]Liu T S,Ren G B.The growth theorem for starlike mappings on bounded starlike circular domains.Chin Ann Math,1998,19B(4):401-408
[6]Liczberski P,Starkov V V.Distortion theorems for biholomorphic convex mappings in Cn.J Math Anal Appl,2002,274:495-504
[7]¨Ozdemir M E,Dragomir S S,Yildiz C.The hadamard inequality for convex function via fractional integrals. Acta Math Sci,2013,33B(5):1293-1299
[8]Arif M,Sok′oi J,Ayaz M.Sufcient condition for functions to be in a class of meromorphic multivalent sakaguchi type spiral-like functions.Acta Math Sci,2014,34B(2):575-578
[9]Liczberski P.New characterization of strongly starlike mappings on balanced pseudoconvex domains in Cn. J Math Anal Appl,2011,384:497-503
[10]Hamada H,Kohr G.Subordination chains and the growth theorem of spirallike mappings.Mathematic (Cluj),2000,42(65):153-161
[11]Lu J,Liu T S,Wang J F.Distortion theorems for subclasses of starlike mappings along a unit direction in Cn.Acta Math Sci,2012,32B(4):1675-1680
[12]Feng S X,Liu T S.Uniformly starlike mappings and uniformly convex mappings on the unit ball Bn.Acta Math Sci,2014,34B(2):435-443
[13]Roper K,Sufridge T J,Convex mappings on the unit ball of Cn.J Anal Math,1995,65:333-347
[14]Graham I.Loewner chains and the Roper-Sufridge extension operator.J Math Anal Appl,2000,247: 448-465
[15]Gong S,Liu T S.The generalized Roper-Sufridge extension operator.J Math Anal Appl,2003,284: 425-434
[16]Liu T S,Xu Q H.Loewner chains associated with the generalized Roper-Sufridge extension operator.J Math Anal Appl,2006,322:107-120
[17]Wang J F.On the growth theorem and the Roper-Sufridge Extension Operator for a class of starlike mappings in Cn.Acta Math Sci,2010,30A(6):1699-1703
[18]Muir J R.A modifcation of the Roper-Sufridge extension operator.Comput Methods Funct Theory,2005, 5:237-251
[19]Wang Jianfei,Liu Taishun.A modifcation of the Roper-Sufridge extension operator for some holomorphic mappings.Chin Ann Math,2010,31A(4):487-496
[20]Chuaqui M.Applications of subordination chains to starlike mappings in Cn.Pacif J Math,1995,168: 33-48
[21]Liu X S.A relation between two subclasses of biholomorphic mappings in several complex variables.Journal of Henan University(Natural Sciance)(in Chinese),2010,40(6):556-559
[22]Hamada H,Kohr G.The growth theorem and quasiconformal extension of strongly spiralike mappings of type α.Complex Variables,2001,44:281-297
[23]Xu Q H,Liu T S.On the growth and covering theorem for normalized biholomorphic mappings.Chin Ann Math,2009,30A(2):213-220
[24]Cai R H,Liu X S.The third and fourth coefcient estimations for the subclasses of strongly spirallike functions.Journal of Zhanjiang Normal College(in Chinese),2010,31(6):38-43
[25]Ahlfors L V.Complex Analysis.New York:Mc Graw-Hill Book Co,1979
?Received June 19,2014;revised January 24,2015.This work is supported by NSF of China(11271359, U1204618),and Science and Technology Research Projects of Henan Provincial Education Department (14B110015,14B110016).
?Corresponding author:Yanyan CUI.
 Acta Mathematica Scientia(English Series)2015年6期
Acta Mathematica Scientia(English Series)2015年6期
- Acta Mathematica Scientia(English Series)的其它文章
- ADDITIVE PERTURBATIONS OF LOCAL C-SEMIGROUPS?
- THEORY AND APPLICATION OF FRACTIONAL STEP CHARACTERISTIC FINITE DIFFERENCE METHOD IN NUMERICAL SIMULATION OF SECOND ORDER ENHANCED OIL PRODUCTION?
- BLOWING UP AND MULTIPLICITY OF SOLUTIONS FOR A FOURTH-ORDER EQUATION WITH CRITICAL NONLINEARITY?
- QUADRATIC ρ-FUNCTIONAL INEQUALITIES IN BANACH SPACES?
- STABILITY OF SOME POSITIVE LINEAR OPERATORS ON COMPACT DISK?
- A NOTE ON THE REPRESENTATIONS FOR THE GENERALIZED DRAZIN INVERSE OF BLOCK MATRICES?
