A NOTE ON THE REPRESENTATIONS FOR THE GENERALIZED DRAZIN INVERSE OF BLOCK MATRICES?

Faculty of Sciences and Mathematics,University of Niˇs,P.O.Box 224,18000 Niˇs,Serbia

E-mail:dijana@pmf.ni.ac.rs

A NOTE ON THE REPRESENTATIONS FOR THE GENERALIZED DRAZIN INVERSE OF BLOCK MATRICES?

Dijana MOSI′C

Faculty of Sciences and Mathematics,University of Niˇs,P.O.Box 224,18000 Niˇs,Serbia

E-mail:dijana@pmf.ni.ac.rs

generalized Drazin inverse;block matrix;Banach algebra

2010 MR Subject Classifcation46H05;47A05;15A09

1 Introduction

Let A be a complex unital Banach algebra with unit 1.For a∈A,we denote by σ(a)the spectrum of a.The sets of all invertible,nilpotent and quasinilpotent elements(σ(a)={0})of A will be denoted by A-1,Aniland Aqnil,respectively.

Let us recall that the generalized Drazin inverse of a∈A(or Koliha-Drazin inverse of a) is the unique element ad∈A which satisfes

The generalized Drazin inverse adexists if and only if 0/∈acc σ(a)(see[1]).It is well-known that aπ=1-aadis the spectral idempotent of a corresponding to the set{0}.We use Adto denote the set of all generalized Drazin invertible elements of A.

The following result is well-known for matrices[2,Theorem 2.1],for bounded linear operators[3,Theorem 2.3]and for elements of Banach algebra[4].

Lemma 1.1([4,Example 4.5])Let a,b∈Adand let ab=0.Then a+b∈Adand

If p=p2∈A is an idempotent,we can represent element a∈A as

where a11=pap,a12=pa(1-p),a21=(1-p)ap,a22=(1-p)a(1-p).

We present well-known result on the generalized Drazin inverse of a triangular block matrix.

Lemma 1.2([4,Theorem 2.3])Let

relative to the idempotent p∈A.If a∈(pAp)dand b∈((1-p)A(1-p))d,then x∈Adand

We state the auxiliary results which are proved for matrices[5]and Banach space operators [6],and they are equally true for elements of Banach algebras.

Lemma 1.3Let p∈A be an idempotent,b∈pA(1-p)and c∈(1-p)Ap.If bc∈(pAp)d, then cb∈((1-p)A(1-p))d,(cb)d=c[(bc)d]2b and b(cb)d=(bc)db.

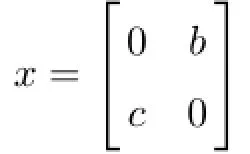
2 Results

Let

relative to the idempotent p∈A,a∈(pAp)dand d∈((1-p)A(1-p))d.

We present the main result which involve new formula for the generalized Drazin inverse of x in terms of adand(bc)dunder some conditions.The following result is a generalization of [6,Theorem 3.8]for the generalized Drazin inverse of an anti-triangular operator matrix.

Theorem 2.1Let x be defned as in(2.1)and let bc∈(pAp)d.If

then x∈Adand

where

ProofWe can write

By the assumptions,we obtain that yz=0.

To prove that y∈Ad,let

Observe that y1y2=0.Since aaπ∈(pAp)qnil,(aaπ)d=0.Using Lemma 1.2,we see that y1∈Adand

From bcaπ=bc∈(pAp)dand Lemma 1.4,we deduce that y2∈Adand

Applying Lemma 1.3,note that caπb∈((1-p)A(1-p))d.So,

實際上，就大部分的協管員的工作崗位而言，工作也不容易，他們經常身兼多職，有時很難做到家家戶戶走訪宣講。有時遇到很多瑣事，也會導致工作中的情緒化，而這種負面情緒也會影響工作質量。也有一些協管員，綜合素質較低，仗著是領導的親戚朋友等關系，對待農民態度蠻橫，很多農民不愿意去他們那里咨詢新農保相關政策。對于不少農民來講，與上層領導的溝通也是很不方便，有時候信息反饋出現嚴重滯后性。有時由于通知不到位，有不少外出務工的農民，無法按時完成參保手續。

and,for n≥0,

Also,for n≥1,

By Lemma 1.1,we deduce that y∈Adand

By Lemma 1.2,we have that z∈Ad,

It follows that zzπ=0 implying z∈A#and z#=zd.Note that z#y1=0.

Using Lemma 1.1,x∈Adand

Notice that the conditions aaπb=0,bcaad=0 and dc=0 of Theorem 2.1 are equivalent with the following geometrical conditions:

where x?={y∈A:xy=0}.

Applying Theorem 2.1,we obtain the next consequences.

Corollary 2.2Let x be defned as in(2.1),d∈((1-p)A(1-p))d,bc∈(pAp)dand dc=0.

(i)If a∈(pAp)qniland ab=0,then x∈Adand

(ii)If bca=0 and a2=a,then x∈Adand

where

(iii)If a∈(pAp)-1and bc=0,then x∈Adand

(iv)If a∈(pAp)d,aπb=0 and caad=0,then x∈Adand

(v)If a∈(pAp)d,aaπb=0 and bca=0,then x∈Adand

where

Proof(i)It follows by ad=0.

(ii)Since ad=a,we prove this part.

The parts(iii)and(v)follow by direct computations.

(iv)From aπb=0 and caad=0,we get cad=0,caπ=c,caad=0,(bc)2=bcaπbc=0, cb=caadb=0 and(bc)d=0.?

Observe that part(ii)of Corollary 2.2 is an extension of[13,Corollary 3.3]for complex matrices.

If the condition d=0 is added in Corollary 2.2,notice that parts(i)-(v)of Corollary 2.2 recover[6,Corollary 4.1-4.5],respectively,which include formulae for the generalized Drazin inverse of an anti-triangular operator matrix.

Now,we consider some expressions for the generalized Drazin inverse of triangular and anti-triangular matrices in Banach algebras which can be obtained using Theorem 2.1.

ProofIf b=0 in Theorem 2.1,we show this result.?

ProofThis result follows by Theorem 2.1 for c=0.? We can see that Corollary 2.3 and Corollary 2.4 are particular cases of[4,Theorem 2.3].

ProofUsing Theorem 2.1 for a=0,we obtain this corollary.?

We next develop necessary and sufcient conditions for the existence and the expressions for the group inverse of an anti-triangular matrix in Banach algebras.

ProofAssume that bc∈(pAp)#,d∈((1-p)A(1-p))#and dc=0.From Lemma 1.3, we deduce that cb∈((1-p)A(1-p))dand(cb)π(cb)2=c(bc)πbcb=0.Denote by u the right hand side of(2.3).Using Corollary 2.5,we have that x∈Adand

The assumption dc=0 implies that d#c=0 and

Observe that x∈A#if and only if x=xdx2.The equality x=xdx2is equivalent to

Since c=c(bc)#bc implies(cb)πcbdd#=c(bc)πbdd#=0,we conclude that x∈A#and x#=u if and only if c(bc)π=0 and(bc)πbdπ=0.?

The next corollary can be proved applying Theorem 2.1 for d=0.

In the following corollary,we obtain the same expression for the generalized Drazin inverse xdas in[14,Theorem 4.4]for the Drazin inverse of an operator matrix.

ProofThis result follows by Theorem 2.1.?

[1]Koliha J J.A generalized Drazin inverse.Glasgow Math J,1996,38:367-381

[2]Hartwig R E,Wang G,Wei Y.Some additive results on Drazin inverse.Linear Algebra Appl,2001,322: 207-217

[3]Djordjevi′c D S,Wei Y.Additive results for the generalized Drazin inverse.J Austral Math Soc,2002,73: 115-125

[4]Castro-Gonz′alez N,Koliha J J.New additive results for the g-Drazin inverse.Proc Roy Soc Edinburgh Sect A,2004,134:1085-1097

[5]Catral M,Olesky D D,Van Den Driessche P.Block representations of the Drazin inverse of a bipartite matrix.Electron J Linear Algebra,2009,18:98-107

[6]Deng C,Wei Y.A note on the Drazin inverse of an anti-triangular matrix.Linear Algebra Appl,2009,431: 1910-1922

[7]Campbell S L,Meyer C D.Generalized Inverses of Linear Transformations.London:Pitman,1979

[8]Bu C,Sun L,Zhou J,Wei Y.Some results on the Drazin inverse of anti-triangular matrices.Linear Multilinear Algebra,2013,61:1568-1576

[9]Castro-Gonz′alez N,Dopazo E.Representations of the Drazin inverse for a class of block matrices.Linear Algebra Appl,2005,400:253-269

[10]Castro-Gonz′alez N,Mart′?nez-Serrano M F.Drazin inverse of partitioned matrices in terms of Banachiewicz-Schur forms.Linear Algebra Appl,2010,432:1691-1702

[11]Deng C,Wei Y.Representations for the Drazin inverse of 2×2 block-operator matrix with singular Schur complement.Linear Algebra Appl,2011,435:2766-2783

[12]Huang J,Shi Y,Chen A.The representation of the Drazin inverse of anti-triangular operator matrices based on resolvent expansions.Appl Math Comput,2014,242:196-201

[13]Li X,Wei Y.A note on the representations for the Drazin inverse of 2×2 block matrix.Linear Algebra Appl,2007,423:332-338

[14]Xu Q,Wei Y,Song C.Explicit characterization of the Drazin index.Linear Algebra Appl,2012,436: 2273-2298

?Received June 2,2014;revised November 28,2014.The work was supported by the Ministry of Education and Science,Republic of Serbia(174007).