基于預報的實時衛星鐘差完好性監測算法比較

吳傳龍，陳 慎，張海濤，劉 夢

（1.61175部隊，湖北武昌430000；2.61243部隊，甘肅蘭州730000）

基于預報的實時衛星鐘差完好性監測算法比較

吳傳龍1，陳 慎1，張海濤1，劉 夢2

（1.61175部隊，湖北武昌430000；2.61243部隊，甘肅蘭州730000）

利用鐘差歷史數據建立衛星鐘差模型，提出了基于預報鐘差的衛星鐘差完好性監測算法，并對比分析了采用最小二乘算法和遺忘因子最小二乘算法對鐘差異常監測的效果，結果表明：遺忘因子最小二乘算法監測效果明顯優于最小二乘算法。

衛星鐘差；完好性；實時監測；遺忘因子最小二乘

0 引 言

衛星鐘差在精密定位中占有重要的地位，鐘差納秒級的誤差引起的等效距離誤差可達分米甚至是米級，其準確與否將直接影響用戶的定位精度，從用戶角度而言，衛星鐘差的完好性比精度有著更加重要的地位，因此，研究衛星鐘差的完好性算法具有重要的現實意義[1］。目前衛星鐘差的完好性監測主要是依靠地基輔助技術實現，利用地面監測站監測衛星鐘的完好性，但其對地面依賴程度高、費用昂貴、及時告警能力差。衛星鐘的完好性監測主要是監測衛星鐘差異常，還可以通過動態Allan方差、平均滑動濾波等算法和基于滑動窗口的最小二乘擬合算法實現，這些算法雖然能夠監測衛星鐘差異常情況，但在實時性上它們很難滿足提供實時定位服務系統的需要，尤其無法滿足基于區域參考站網絡的實時精密單點定位[2－6］。本文提出利用鐘差歷史數據建立衛星鐘差模型，采用實時更新的固定長度的鐘差數據的算法實時監測衛星鐘差異常，并通過實驗進行了驗證。

1 衛星鐘差完好性監測算法

1.1 衛星鐘差預報模型

衛星鐘差完好性監測需要衛星鐘時鐘頻率具有足夠的穩定性，以保證時鐘偏差是可以預測的，一般采用二次多項式模型，表示為矩陣形式[6－7］為

式中，H為n×3維設計矩陣

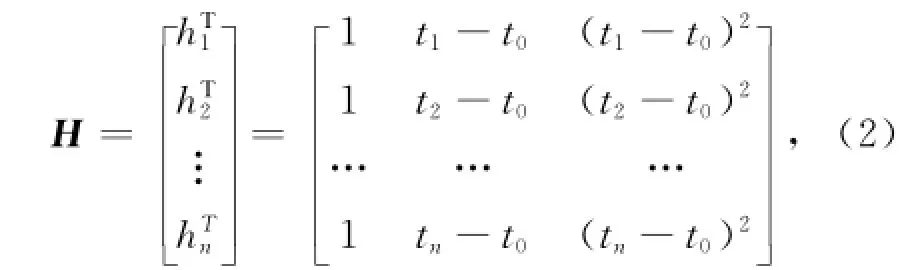
式中：X為n維觀測向量；a＝[a0a1a2］T為3維未知參數向量，a0、a1和a2分別表示衛星在參考時刻t0時的鐘差、鐘速和鐘速變化率；e為n維誤差向量。可得最小二乘解

普通最小二乘解算衛星鐘差模型參數時，采用單位陣作為觀測值權矩陣，即將新老鐘差觀測數據統一對待，但對于預報而言，離預報時刻越近的觀測數據與后續預報結果的相關性越強，對預報鐘差的貢獻也越大。因此，在解算鐘差模型參數時，把單位陣當作觀測值權矩陣是不合理的[8］。為了離預報時刻越近的觀測數據對預報模型的貢獻，削弱老數據的影響，可以引入遺忘因子矩陣作為觀測權矩陣。取遺忘因子不同的值就可以得到不同的遺忘效果[8］。若已知遺忘因子為λ，則遺忘因子矩陣W

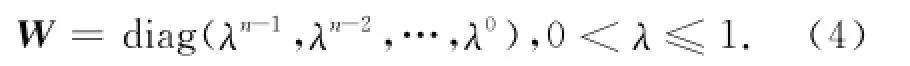
在采用以前的全部觀測數據進行衛星鐘差的預報衛星鐘差，隨著觀測數據時間的增加，會造成數據飽和，降低參數估計的速度和效率，顯然不能用以前所有的全部觀測量進行衛星鐘差的預報，可以采用實時更新的固定的一定長度的鐘差數據對衛星鐘差進行擬合預報。

1.2 衛星鐘差完好性監測算法步驟

衛星鐘的完好性監測主要是監測衛星鐘差異常，其具體步驟如下

1）建立衛星鐘差模型，利用實時更新的一定長度的鐘差數據實時預報衛星鐘差。在衛星鐘異常監測算法中，實時更新的數據長度是很重要的，數據長度決定了預報鐘差的精度，長度越大預報鐘差精度越高，處理器負擔也越大，影響系統的實時性，在實際處理中固定數據長度可以在20～100之間取值。

2）計算統計檢驗量及監測門限，判斷是否發生異常。

若利用參考站網絡實時解算出的衛星鐘差為x（n）solve，預報鐘差為x（n）pre，則可構造統計監測量z（n＋1）為

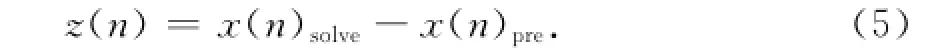
已知實時解算鐘差標準偏差σsolve、預報鐘差的標準偏差σpre，根據方程（5），利用協方差傳播定律可得z的方差結果：

3）如果鐘差數據沒有發生異常，則利用正常結算得到的鐘差數據，實時更新衛星鐘差預報模型；若鐘差數據發生異常，則對鐘差異常數據進行剔除，并利用實時輸出的預報鐘差代替異常值對鐘差預報模型進行更新，預報下一歷元，從而完成異常數據的替換。

2 實驗分析

為了能夠更好的驗證文中算法的監測效果，采用IGS網站提供的事后精密衛星鐘差產品進行實驗分析，數據為2012年1月27日采樣間隔為30s的數據。根據表1隨機選取不同類型的四顆衛星進行試驗分析，這四顆星分別是8號Block IIA銫鐘、17號Block IIR－M銣鐘、18號Block IIR銣鐘及26號Block IIA銣鐘。設計了兩種試驗方案進行衛星鐘完好性監測分析，兩種方案均利用實時更新的長度一定的鐘差數據實時預報衛星鐘差，進而實現衛星鐘差的異常監測，均固定實時更新數據的長度為100.其中，方案一采用最小二乘算法（LS），方案二采用遺忘因子最小二乘算法（FFLS）。

2.1 衛星鐘差預報性能分析

由衛星鐘差異常監測原理可知，衛星鐘差異常監測的能力與衛星鐘差的預報精度有很大關系，圖1～圖4分別給出了采用不同方法對8、17、18和26四顆衛星的鐘差預報誤差圖，表1示出了兩種方案對四顆衛星鐘差的預報精度。

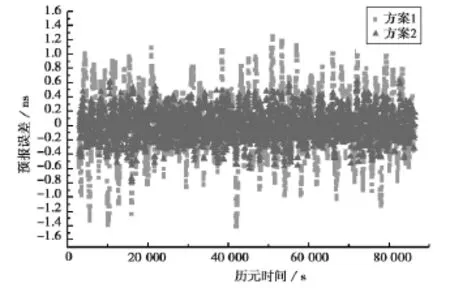
圖1 8號衛星鐘差預報誤差

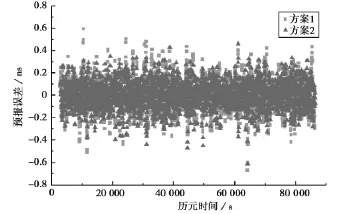
圖2 17號衛星鐘差預報誤差

圖3 18號衛星鐘差預報誤差

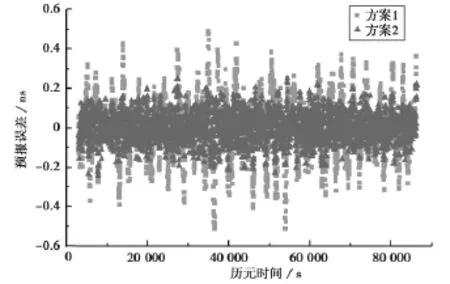
圖4 26號衛星鐘差預報誤差

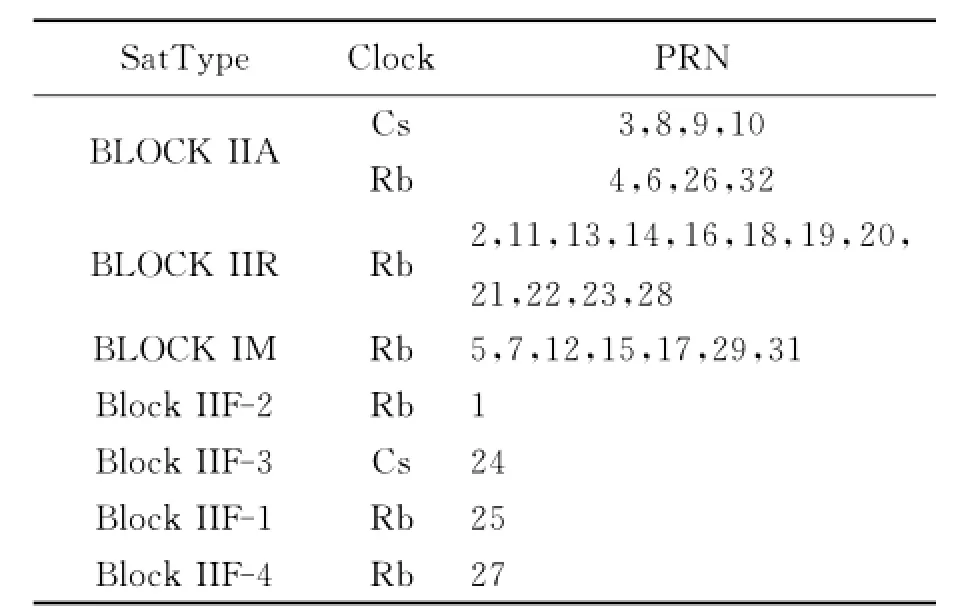
表1 GPS衛星鐘類型和衛星號對照表

采用相同算法預報的不同衛星鐘差的精度并不相同，通常情況下，原子鐘越穩定預報效果越好，但由圖1～圖4和表2可知，采用最小二乘算法時，原子鐘性能較好的17號和18號衛星的預報精度與穩定性較差的26號衛星預報精度基本相當，采用遺忘因子最小二乘算法時，穩定性較差的26號星的預報精度反而好于穩定性較好的17號和18號衛星，這主要是因為在這種小樣本的超短期鐘差預報中，預報鐘差的精度雖與衛星鐘的穩定性有關，但更主要的是取決于衛星鐘鐘差在該時段內的小尺度變化[9－10］。對同一衛星而言，FFLS算法具有波動相對較小的特點，對衛星鐘差的預報精度優于LS算法。采用FFLS算法分別可以將四顆衛星的鐘差預報精度從0.46ns、0.15ns、0.14ns、0.15ns分別提高到0.21ns、0.12ns、0.12ns、0.07ns，尤其是對于對8號和26衛星的鐘差預報精度提高較為明顯，考慮到這兩顆衛星分別為已經工作了20多年的Block IIA銫鐘和Block IIA銣鐘，原子鐘的穩定性相對較低，因此可以得出結論衛星鐘穩定性越差，采用FFLS算法對鐘差預報精度提高越明顯，越能體現出FFLS算法的優越性。

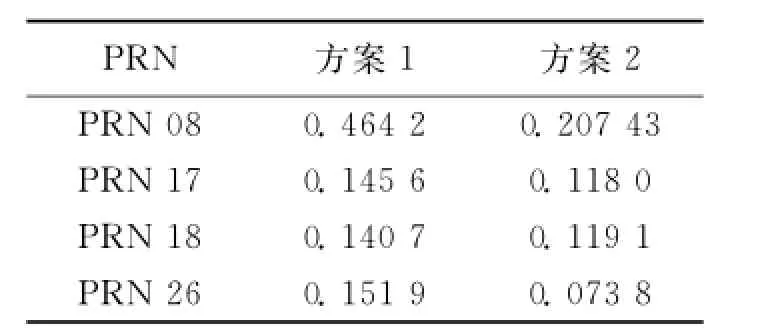
表2 三方案鐘差預報精度RMS（單位：ns）

2.2 衛星鐘差異常監測性能分析

為了能更好的驗證算法的監測效果，本文通過對IGS事后精密鐘差數據加入異常數據模擬異常發生的情況，對算法進行驗證和分析。誤警概率取為1/15 000，計算一天數據，統計能夠準確探測出異常的百分比。圖5示出了8、17、18和26四顆衛星采用兩種方法探測出鐘差異常的成功率隨加入的鐘差異常值大小的曲線變化。

圖5 鐘差異常探測成功率曲線

從圖5可以看出，鐘差異常檢測成功率隨著加入鐘差異常值的增大而增大。當探測成功率達到99%時，采用LS算法，8、17、18和26四顆衛星能探測出的最小鐘差異常分別為2.265、0.650、0.900、0.950；采用FFLS算法，四顆衛星能探測出的最小鐘差異常分別為1.225、0.550、0.775、0.575.顯然，對于同一顆衛星，FFLS算法的異常監測能力明顯高于LS算法，尤其是對衛星鐘穩定性越差8號衛星，探測能力提高的更為明顯，能夠將檢測出的鐘差異常從2.265ns提高到1.225ns.

3 結束語

衛星鐘差精度直接影響高精度用戶的定位結果，實時定位系統中，在提供實時精密衛星鐘差產品的同時，還應當實時提供鐘差完好性信息，因此應當對衛星鐘差異常進行實時監測。本文基于鐘差預報值實現了衛星鐘差的完好性算法，在鐘差擬合預報模型基礎上，實時得到衛星鐘差預報值，將實時解算的衛星鐘差與預報鐘差比較，來實時對衛星鐘差異常進行監測，試驗結果表明：FFLS算法鐘差預報精度和鐘差完好性監測能力均明顯高于LS算法，并且FFLS算法方法簡便易行，應用靈活，比較適用于衛星鐘差完好性的實時監測。

[1]方書山.GPS衛星鐘差完備性監測研究與算法實現[D］.阜新：遼寧工程技術大學，2011：19－35.

[2]唐 升，劉 婭，李孝輝.星載原子鐘自主完好性監測方法研究[J］.宇航學報，2013，34（1）：39－45.

[3]牛 飛，韓春好，張義生，等.導航衛星星載原子鐘異常監測分析[J］.武漢大學學報·信息科學版，2009，34（5）：585－588.

[4]RODRIGUEZ I，GARCFA C，CATALAN C，et al.Satellite autonomous integrity monitoring（SAIM）for GNSS systems[C］//ION GNSS 2009，2009.

[5]黃新明，龔 航，朱祥維，等.基于Kalman濾波器的衛星鐘實時異常監測算法[J］.宇航計測技術，2011，31（5）：6－11.

[6]許龍霞，李孝輝.基于接收機鐘差的GPS完好性自主檢測算法[J］.宇航學報，2011，32（3）：537－542.

[7]黃觀文.GNSS星載原子鐘質量評價及精密鐘差算法研究[D］.西安：長安大學，2012.

[8]宋 成，王雪飛，莊釗文.基于遺忘因子最小二乘的GPS接收機鐘差預測算法研究[J］.測繪科學，2008（s1）：41－43.

[9]郭海榮.導航衛星原子鐘時頻特性分析理論與方法研究[D］.鄭州：信息工程大學，2006：143－161.

[10]于合理，郝金明，劉偉平，等.衛星鐘差超短期預報模型分析[J］.大地測量與地球動力學，2014，34（1）：161－164.

Real－Time Integrity Monitoring Algorithm of Satellite Clock Based on Prediction

WU Chuanlong1，CHEN Shen1，ZHANG Haitao1，LIU Meng2
（1.61175 Troops of PLA，Wuchang430000，China；2.61243 Troops of PLA，Lanzhou730000，China）

The model of satellite clock error was established based on historical data，a real－time integrity monitoring algorithm of satellite clock was proposed，and comparative analysis the effect of integrity monitoring by using the least squares algorithm and forgetting factor least squares algorithm.The results showed that：forgetting factor least squares algorithm is better than the least－squares algorithm to monitor.

Satellite clock error；integrity；real－time monitoring；the forgetting factor least square algorithm

P228.4

A

1008－9268（2015）01－0023－04

10.13442/j.gnss.1008－9268.2015.01.005

吳傳龍（1987－），男，湖北天門人，助理工程師，主要從事大地測量和衛星導航定位研究。

陳 慎（1986－），男，湖北應城人，助理工程師，主要從事大地測量和衛星導航定位研究。

張海濤（1986－），男，湖南澧縣人，助理工程師，主要從事大地測量和衛星導航定位研究。

劉 夢（1978－），女，山東萊蕪人，工程師，主要從事測量數據處理和地圖編繪工作。

2014－11－03

聯系人：吳傳龍E－mail：wuchuanlong1987＠163.com