SOM網絡在雷達目標識別中的應用

王 龍 杜敦偉 白艷萍

（1.中北大學理學院，山西 太原 030051；2.北京機電工程研究所，中國 北京 100074）

0 引言

雷達是戰場信息處理系統最基本、最直接、最重要的信息來源之一，對雷達系統進行數字化和信息化改造，增加自動目標識別功能，是現代雷達武器系統的發展方向。識別系統中采用的識別算法是整個系統的核心和中樞環節。因此，識別算法是否具備原理簡單、結構合理、人工調整參數少以及性能穩定等特點，不僅決定識別系統的綜合分類能力，而且直接影響著系統維護與擴展的難易程度和穩健性[1]。

人工神經網絡模擬生物神經系統結構和信息處理機制，具有自組織、自學習等性能，允許樣本存在缺損和畸變，具有對不確定性問題的學習與適應能力，被越來越多地應用與目標識別領域中[2]。自組織特征映射網絡[3](Self-Organizing Feature Map,SOM)作為一類無監督學習的神經網絡模型，可以對外界未知環境或樣本空間進行學習或者模擬，不需要先驗知識，與BP神經網絡[4]等方法相比更適合用于雷達目標識別。

1 SOM神經網絡原理

自組織特征映射網絡 (Self-Organizing Feature Map,SOM)也稱Kohonen網絡，它是由荷蘭學者Teuvo Kohonen于1981年提出的。該網絡是一個由全連接的神經元陣列組成的無教師、自組織、自學習的網絡，實現從輸入空間(n維)到輸出平面(二維)的低維映射，并且映射具有拓撲特征保持性質，通過不斷地調整網絡節點連接權值，自動地尋找樣本數據類型間的內在特征并進行聚類[5]。

1.1 SOM神經網絡結構

典型的SOM網絡結構如圖1所示，由輸入層和競爭層組成。第一層為輸入層，輸入層神經元個數同輸入樣本向量維數一致；第二層為競爭層，競爭層節點呈全連接二維陣列分布，輸入節點和競爭節點之間以可變權值連接。

1.2 SOM神經網絡學習算法

自組織特征映射算法能夠自動找出輸入數據之間的類似度，將相似的輸入在網絡上就近配置，因此是一種可以構成對輸入數據有選擇地給予反應的網絡。自組織特征映射的學習算法步驟如下[5]：

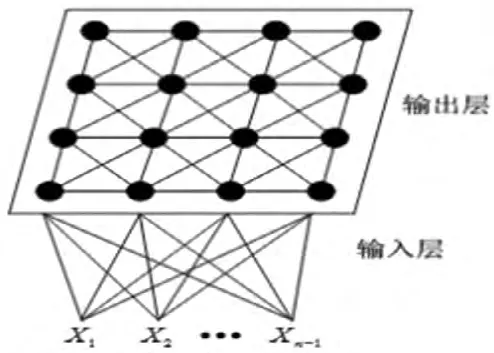
圖1 二維陣列SOM神經網絡模型

（1）網絡初始化

用隨機數設定輸入層和映射層之間的權值的初始值。對m個輸入神經元到輸出神經元的鏈接權值賦予較小的權值。選取輸出神經元j個“鄰接神經元”的集合Sj。其中，Sj(0)表示時刻t＝0的神經元j的“鄰接神經元”的集合，Sj(t)表示時刻t的神經元j的“鄰接神經元”的集合。區域Sj(t)隨著時間的增長而不斷縮小。

（2）確定輸入向量

把輸入向量X＝(x1,x2,…xm)T輸入給輸入層。

（3）尋找獲勝神經元

在映射層，計算各神經元的權值向量和輸入向量的歐氏距離。映射層的第j個神經元和輸入向量的距離計算公式如下：

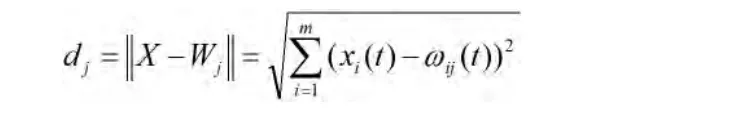
其中，ωij為輸入層的i神經元和映射層的j神經元之間的權值。通過計算，得到一個具有最小距離的神經元，將其稱為勝出神經元，記為j*，即確定出某個單元k，使得對于任意的j，都有dk＝min(dj)，并給出

j其鄰接神經元集合。

（4）權值的調整

修正輸出神經元j*及其“鄰接神經元”的權值：

Δωij=ωij(t+1)-ωij(t)＝η(t)(xij(t)-ωij(t))

式中，η為一個大于0小于1的常數，隨著時間變化逐漸下降到0。

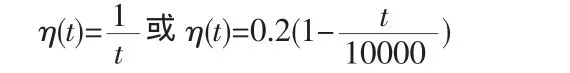
（5）計算輸出 ok

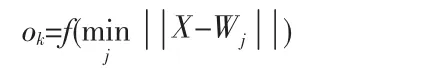
式中，f(*)一般為0-1函數或者其他非線性函數。

（6）驗證結果

如達到要求（此要求根據具體問題具體確定）則算法結束；否則返回步驟（2），進行下一輪學習。

2 雷達目標識別實驗

2.1 實驗場景及數據說明

本實驗的場景以及場景的三維回波顯示如圖2所示。

其中，圖2中主要包含三種特征信息：公路、草地和車輛。兩條高速公路穿過一片草地，在上行高速公路中運行著五輛小轎車和一輛大卡車。本實驗的目的是準確識別出各個車輛的位置。

首先，利用統計的方法，選取合適的閾值，去除孤立點和不合理的聚集點，會得到非常好的結果。但是，此方法的閾值都是符合具體問題的，具有窮舉性，不具有通用性。

圖2 場景以其三維回波顯示圖

2.2 評價指標

針對此問題，本文定義了三個評價指標，分別為最小距離和D、信息覆蓋率ρ和冗余信息率ζ。

最小距離和：本文第二章中，用統計的方法選取合適的閾值，會得到雷達目標點的集合A。本文中集合A會作為標準目標點，用其它算法得到的雷達目標點集合記為S，那么S中每個點到A的所有點的最小距離求和，就是最小距離和D。計算公式如下：

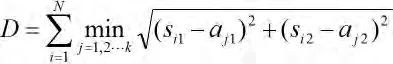
式中，aj1,aj2分別為集合A中第j個點的橫縱坐標值；si1,si2分別為集合S中第i個點的橫縱坐標值。

信息覆蓋率：集合A和集合S中位置相同的目標點占集合A的比例，計算公式如下：

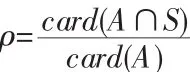
冗余信息率：集合S中除去集合A和集合S中位置相同的目標點，其余的目標點占集合A的比例，計算公式如下：

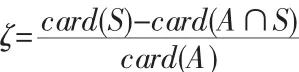
通過評價指標的定義，我們可以知道，最小距離和D和冗余信息率ζ越趨近于0越好，而信息覆蓋率ρ越趨近于1越好。

3 實驗結果

文獻[2]中，提出競爭層神經元的個數應為聚類類別的1.5～2.5倍，因此，本實驗選取從5×5到12×12幾個類別進行比較分析。進行200次實驗，計算平均值進行統計分析，得到表1：

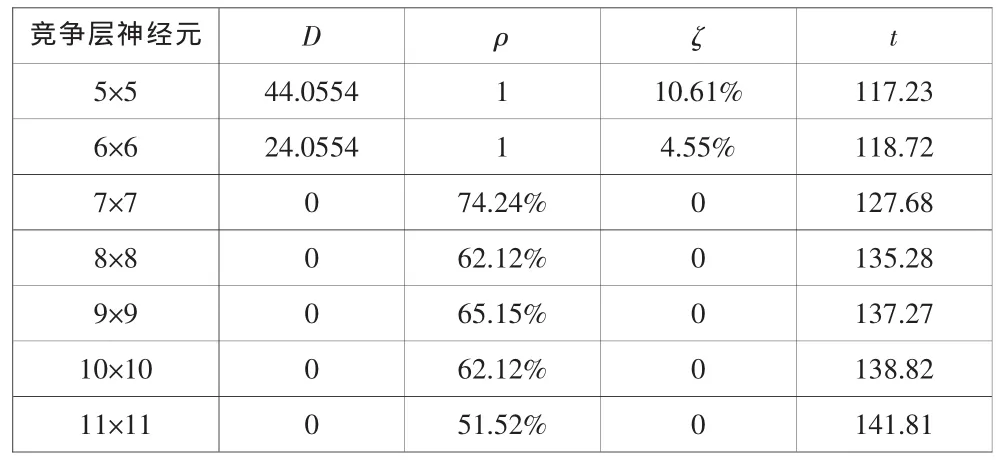
表1 實驗結果

從表1中，我們可以知道，隨著競爭層神經元個數的增加，最小距離和D越來越小，最后變為0，而信息覆蓋率ρ由1慢慢變少，冗余信息率ζ也會也來越少，直至變為0，但是運行時間t會變得越來越長。通過比較，我們發現當競爭層神經元為6×6時，各個指標最好。于是得到如圖3所示的目標點相對位置圖。

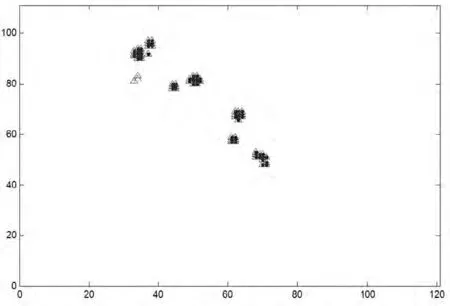
圖3 聚類結果和統計方法的目標點位置對比圖

其中，圖3中三角形是SOM網絡得到的目標點位置即S，實心圓點是統計的方法得到的目標點位置即A。

4 結論

本文針對現有的雷達目標識別問題，采用了無監督的SOM網絡得到了較為理想的結果。但是還是存在一些不足，如：學習率的選取，本文只是選取了η＝0.9，不具有普遍性，下一步的改進方向就可以是把學習率改為學習函數，這樣，可以根據前一步或者前幾步的學習速率，自動的調整其大小。另外，還可以把粒子群算法(PSO)引入其中，進行權值訓練，加快運行速度。總之，SOM網絡在雷達目標識別中具有其特有的優勢。

［1］郁文賢.智能化識別方法及其在艦船雷達目標識別系統中的應用[D].長沙：國防科技大學,1992．

［2］Bishop C M.Neural networks for pattern recognition[M].Oxford,England：Oxford University Press,1996：1-28.

［3］涂曉芝,顏學峰,錢鋒.基于SOM網絡的基因表達數據聚類分析[J].華東理工大學學報：自然科學版,2006,32(8)：992-996.

［4］張靜,宋銳,郁文賢.雷達目標識別中的BP神經網絡算法改進及應用[J].系統工程與電子技術,2005,27(4)：582-585.

［5］王小川,史峰,郁磊,李洋.MATLAB神經網絡 43個案例分析[M].北京：北京航空航天大學出版社,2013：186-195.