具有時滯的兩種群Lotka-Volterra 合作系統的穩定性

陳曉英， 韓榮玉

(1. 福州大學至誠學院 計算機工程系，福建 福州350002;2. 福州大學 數學與計算機科學學院，福建福州350108)

1 引 言

經典的兩種群Lotka-Volterra 合作系統可以表示為

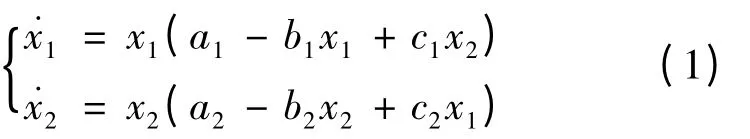
由文獻［1－2］，對該系統而言，條件

足以保證系統(1)存在唯一的全局吸引的正平衡點。

近來，許多學者對合作系統的持久性及穩定性問題進行了研究，讀者可參考文獻［3－6］及其引文文獻。考慮到現實的生物數學模型不可避免地都要受到歷史狀態的影響，LIN Suqing，LU Zhengyi［3］考慮了具有時滯的合作系統，研究了如下模型:

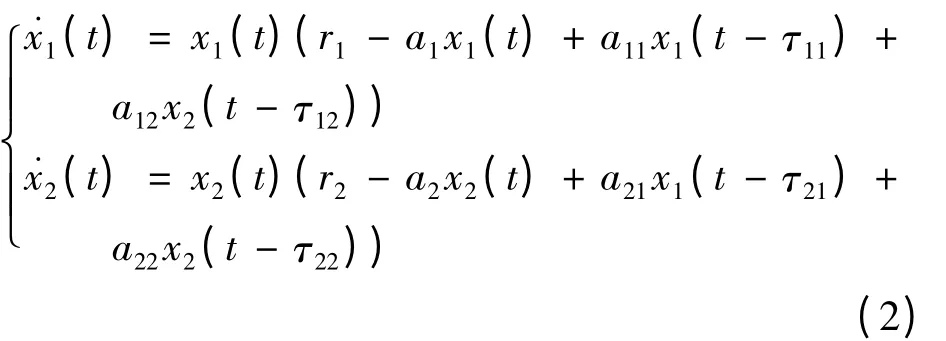
其中ri，ai，aij，τij(i，j = 1，2)均為常數，且ai＞0，τij≥0(i，j = 1，2)，考慮條件:

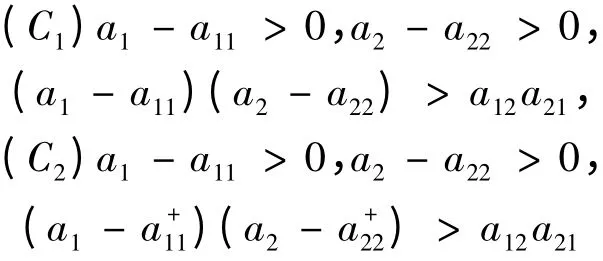
文中旨在發展文獻［8－9］的研究技巧，通過構造適當的Lyapunov 泛函，得到保證系統正平衡點全局吸引的充分性條件，所得結果補充和完善了前人的結果。

2 主要結果

基于系統的生態學意義，文中恒設系統(2)滿足如下初始條件:

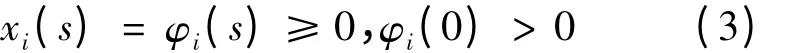
式中，φi(s)(i = 1，2)是［－ τ，0］上的連續函數，τ =max{τij:i，j = 1，2}。

引理1 系統(2)滿足初始條件(3)的解x1(t)＞0，x2(t)＞0(t ≥0)。

證

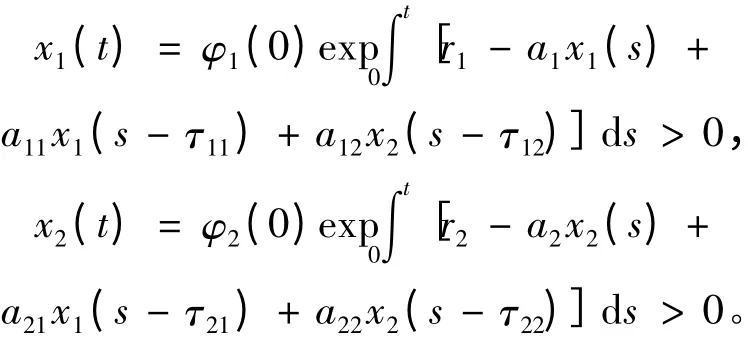
作為LIN Suqing，LU Zhengyi［3］定理2.2 的直接推論，關于系統(2)的持久性，有

引理2 若條件(C2)成立，系統(2)，(3)是持久的，即存在與系統的解無關的正常數m 和M 使得系統(2)的任一正解均滿足:

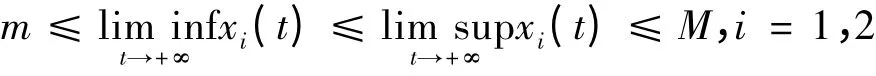
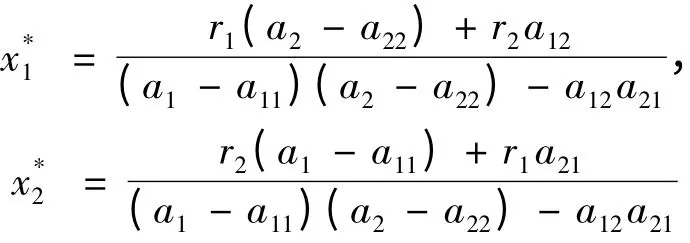
下面，考慮條件

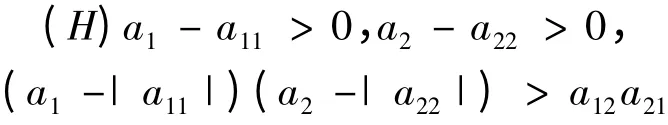
證 構造Lyapunov 函數:

沿著系統(2)～(3)的解計算V1(t)的導數，有

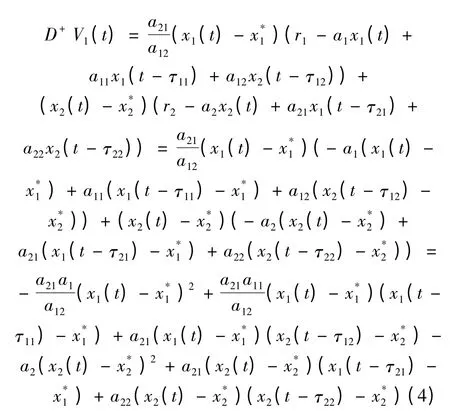
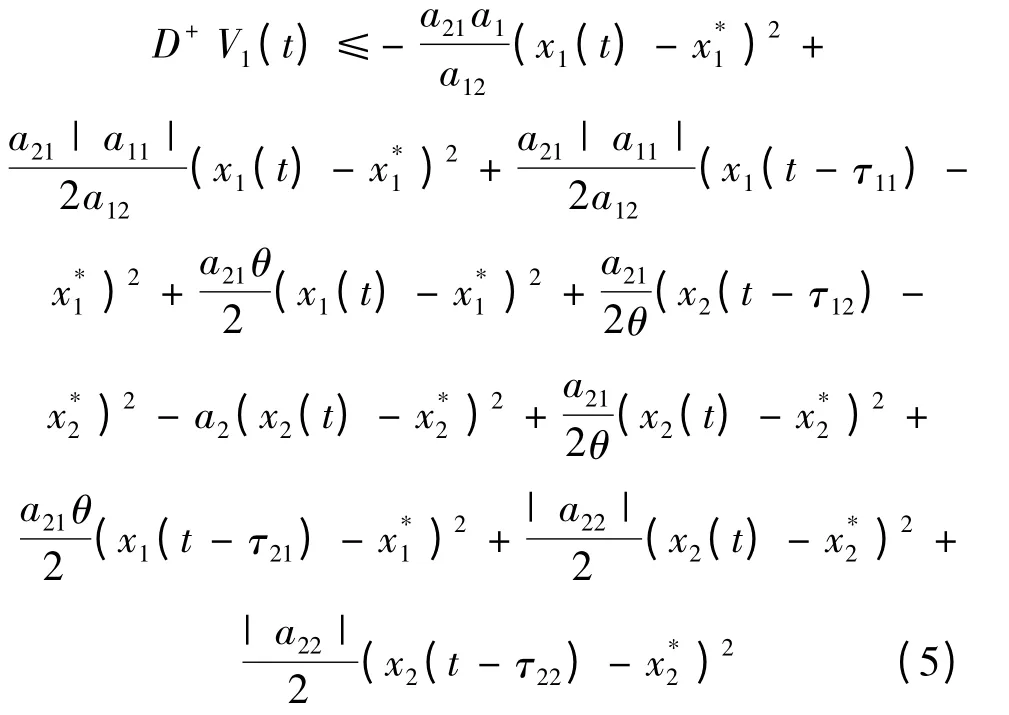
令

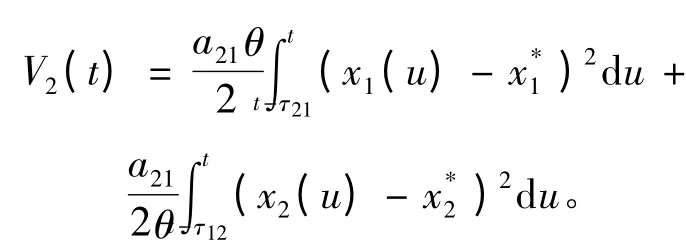
計算V2(t)的導數，有

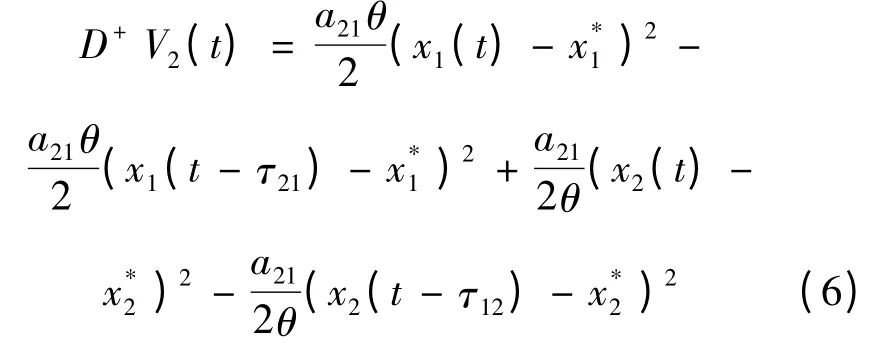
令

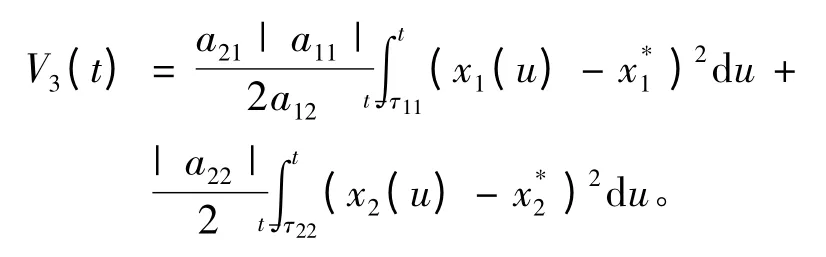
計算V3(t)的導數，有

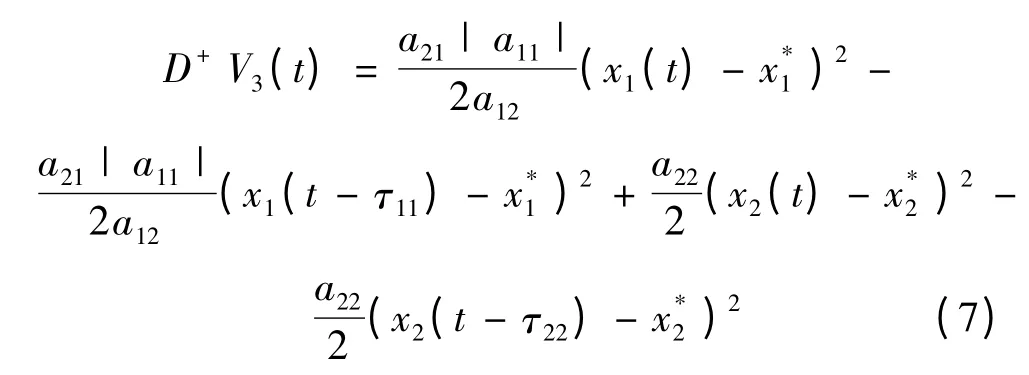
定義

由式(5)，(6)，(7)可知，有

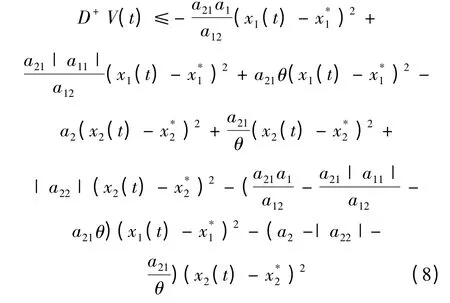
取

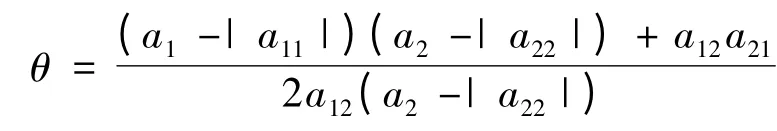
由條件H 則有

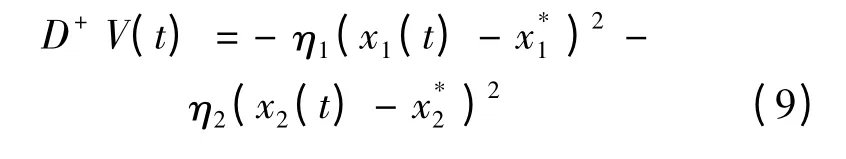
其中

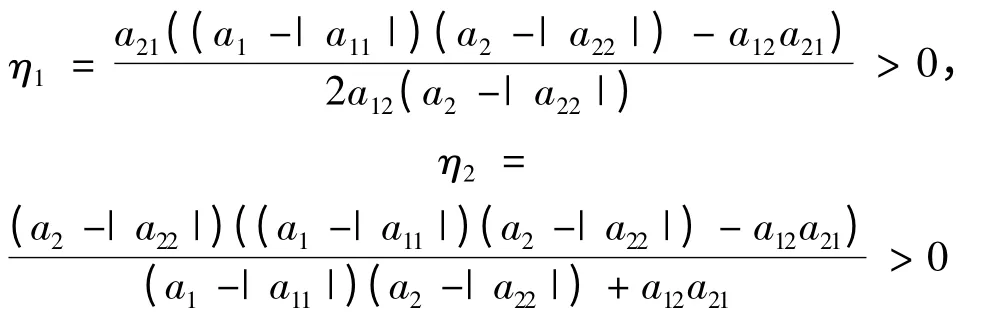
由式(9)可知，有

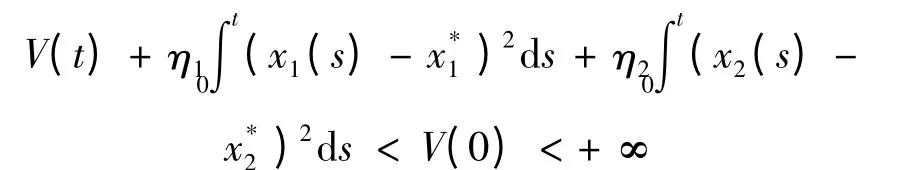
令t →+ ∞，有

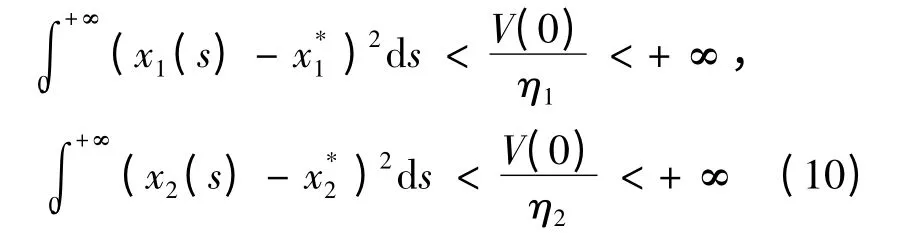
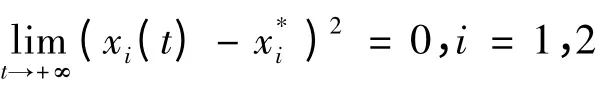
也就是有

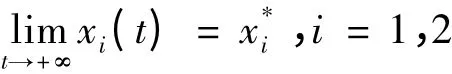
注 定理表明，條件(H)足以保證系統的正平衡點的全局吸引的，注意到，條件(H)蘊含了條件(C1)和(C2)，文中結果是對已有結果LIN Suqing，LU Zhengyi［3］的補充和完善。

［1］馬知恩.種群生態學的數學建模與研究［M］.合肥:安徽教育出版社，1996.

［2］陳蘭蓀，宋新宇，陸征一.數學生態學模型與研究方法［M］.成都:四川科學技術出版社，2003.

［3］LIN Suqing，LU Zhengyi. Permanence for two-species Lotka-Volterra systems with delays［J］. Mathematical Biosciences and Engingeering，2006，3(1):137-144.

［4］陳鳳德，陳婉琳，趙亮.具有離散時滯的兩種群合作系統的穩定性［J］.沈陽大學學報:自然科學版，2013，25(5):376-378.

CHEN Fengde，CHEN Wanlin，ZHAO Liang. Stability of two species cooperative system with discrete delay［J］. Journal of Shenyang University:Natural Science，2013，25(5):376-378.(in Chinese)

［5］楊坤，王海娜，陳鳳德.反饋控制Lotka-Volterra 合作系統穩定性研究［J］.應用數學，2014，27(2):243-247.

YANG Kun，WANG Haina，CHEN Fengde.On the stability property of Lotka-Volerra Cooperation system with feedback controls［J］.Mathematica Applicata，2014，27(2):243-247.(in Chinese)

［6］LU Guichen，LU Zhengyi，LIAN Xinze. Delay effect on the permanence for Lotka-Volterra copperative systems［J］. Nonlinear Analysis:Real World Applications，2010，11(4):2810-2816.

［7］陳鳳德，謝向東.合作種群模型動力學研究［M］.北京:科學出版社，2014.

［8］LI Zhong，HAN Maoan，CHEN Fengde.Influence of feedback controls on an autonomous Lotka-Volterra competitive system with infinite delays［J］.Nonlinear Analysis:Real World Applications，2013，14(1):402-413.

［9］CHEN Fengde. Global stability of a single species model with feedback control and distributed time delay［J］. Applied Mathematics and Computation，2006，178(2):474-479.