乘積圖的Hyper-Wiener 指標(biāo)

陳育櫟

(福州大學(xué)至誠學(xué)院 計(jì)算機(jī)工程系，福州 福建350002)

在化學(xué)理論中，分子的化學(xué)和物理性能一般可用分子圖的拓?fù)渲笜?biāo)反映出來，而不同的分子拓?fù)渲笜?biāo)反映出該分子的不同性能，所以在化學(xué)界出現(xiàn)了很多種重要的分子拓?fù)渲笜?biāo)。基于分子圖的頂點(diǎn)間距離的拓?fù)渲笜?biāo)對(duì)刻畫分子圖以及建立分子結(jié)構(gòu)和特征間的關(guān)系有重要作用，同時(shí)被廣泛用于預(yù)測(cè)化合物的物理化學(xué)性質(zhì)和生物活性，因此具有重要的理論價(jià)值和應(yīng)用背景。Wiener 指標(biāo)是研究最為廣泛的拓?fù)渲笜?biāo)之一，它是Wiener 于1947 年考察烷烴的沸點(diǎn)與分子結(jié)構(gòu)的關(guān)系時(shí)最先提出的。在Wiener 指標(biāo)的基礎(chǔ)之上，1993 年Randi＇c 提出了無圈圖的hyper-Wiener 指標(biāo)的定義。

關(guān)于圖的Wiener 指標(biāo)和hyper-Wiener 指標(biāo)的數(shù)學(xué)性質(zhì)和化學(xué)應(yīng)用見文獻(xiàn)［1-6］。有關(guān)連通圖的Wiener 指標(biāo)和hyper-Wiener 指標(biāo)的研究已經(jīng)有很多好的結(jié)果，但對(duì)兩個(gè)圖的乘積圖的hyper-Wiener指標(biāo)的研究相對(duì)較少，文中主要研究乘積圖的hyper-Wiener 指標(biāo)的性質(zhì)，并給出直積圖的hyper-Wiener 指標(biāo)的計(jì)算公式。

1 乘積圖的介紹

圖的直積是一種直觀且自然的構(gòu)建，曾經(jīng)得到廣泛研究和探討。直積具有大量的代數(shù)性質(zhì)，也被認(rèn)為是圖與圖的所有乘積運(yùn)算中最簡(jiǎn)單的一種。兩個(gè)圖G 和H 的直積G × H 定義如下:

定義1 G × H 點(diǎn)集為

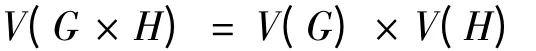
邊集為

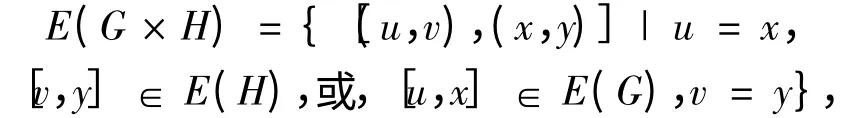
根據(jù)直積圖的定義，容易得到直積圖中頂點(diǎn)的個(gè)數(shù)為

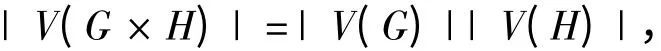
邊的個(gè)數(shù)為

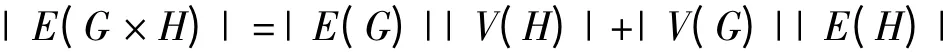
定義2 字典序積圖G［H］的點(diǎn)集為

邊集為

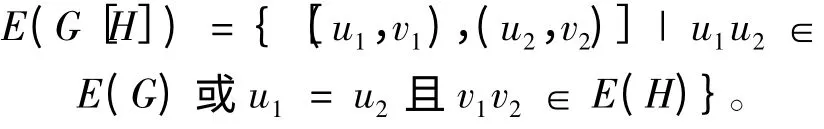
根據(jù)字典序積圖的定義可以觀察到:字典序積G［H］可以看作將圖G 的每個(gè)頂點(diǎn)(如u1，u2)替換成圖H 的拷貝Hu1Hu2，點(diǎn)集Hu1中所有點(diǎn)與Hu2中的所有點(diǎn)當(dāng)u1u2∈E(G)時(shí)相鄰。定義3 聯(lián)接圖G + H 的點(diǎn)集為

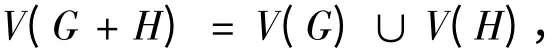
邊集為聯(lián)接點(diǎn)集V(G)與V(H)中頂點(diǎn)的邊的集合(即每條邊的兩個(gè)端點(diǎn)一個(gè)是G 中的點(diǎn)，另一個(gè)是H中的點(diǎn))。

定義4 分離圖G ∨H 的點(diǎn)集為

邊集為

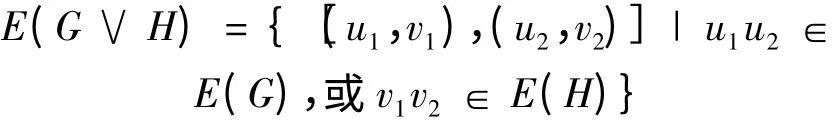
Fath-Tabar 和Ashrafi［7］通過上述所定義的乘積圖點(diǎn)和邊之間的關(guān)系，刻畫出以上乘積圖中任意兩點(diǎn)間的距離:

1)如果G 是| V(G)| ＞1 的連通圖，那么對(duì)字典序積圖G［H］中的任意兩點(diǎn)(u1，v1)，(u2，v2)，根據(jù)定義得到其間的距離關(guān)系，具體刻畫如下:

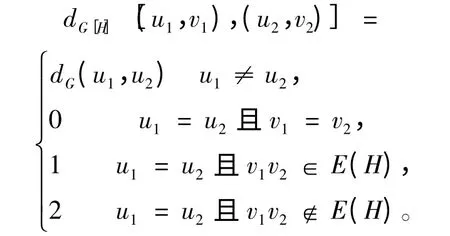
2)聯(lián)接圖G + H 中的任意兩點(diǎn)u，v 間的距離:

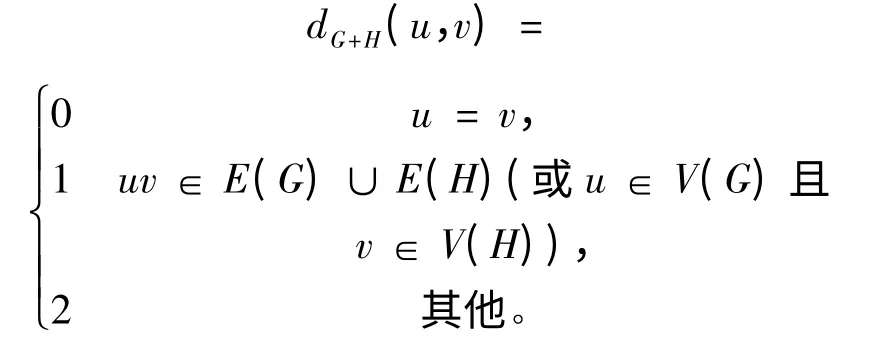
3)分離圖G ∨H 的中任意兩點(diǎn)(a，b)，(c，d)間的距離:

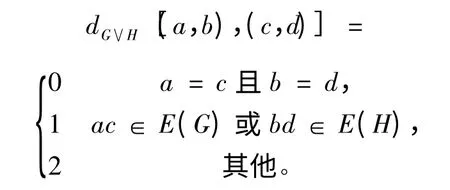
通過刻畫以上乘積圖中點(diǎn)與點(diǎn)的距離規(guī)律，F(xiàn)ath-Tabar 和Ashrafi［7］得到了以上幾類乘積圖的hyper-Wiener 指標(biāo)。受到該思想啟發(fā)，文中研究任意兩個(gè)連通圖的直積圖的hyper-Wiener 指標(biāo)性質(zhì)，并給出直積圖的hyper-Wiener 指標(biāo)的計(jì)算公式。

2 主要結(jié)果

根據(jù)定義1，觀察直積圖(也稱為笛卡爾乘積圖)的結(jié)構(gòu)可以得到以下性質(zhì):

性質(zhì)1 如果(a，b)，(x，y)是乘積圖G × H 的兩個(gè)點(diǎn)，那么其間的距離如下:

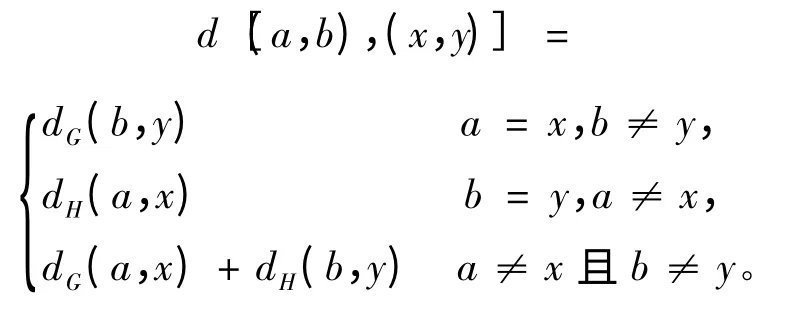
由以上直積圖中兩點(diǎn)之間的距離關(guān)系可以得到文中的主要結(jié)論。

引理1 設(shè)Pm和Pn是頂點(diǎn)數(shù)分別為| V(Pm)| =m，| V(Pn)| = n 的路圖，則有:

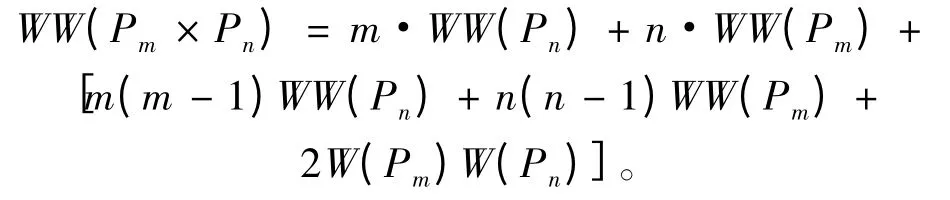
證 路與路的直積圖Pm× Pn，設(shè)Pm= xi1xi2…xim，Pn= xj1xj2…xjn，由Pm和Pn的直積圖Pm× Pn的定義得到圖上任意兩點(diǎn)間的距離應(yīng)滿足下面的關(guān)系式:

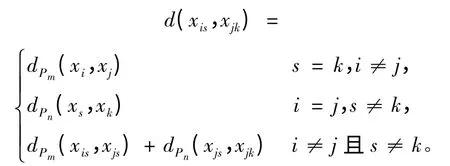
結(jié)合hyper-Wiener 指標(biāo)的定義可以得到:

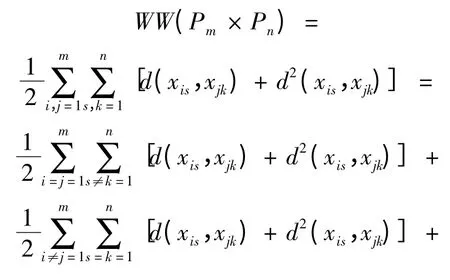
證畢。

現(xiàn)在考慮圈和路的直積圖Cm×Pn，同理可以證明下面的結(jié)果:

定理1 設(shè)Cm和Pn分別是點(diǎn)數(shù)| V(Cm)| = m，| V(Pn)| =n 的圈和路圖，則有:

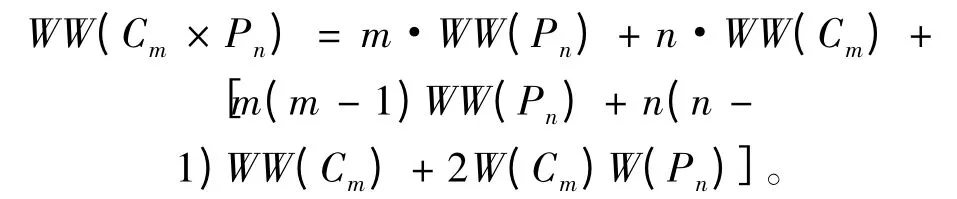
證 現(xiàn)考慮圈與路的直積圖Cm× Pn，由直積圖的結(jié)構(gòu)考慮其中點(diǎn)同樣存在性質(zhì)1 中刻畫的距離關(guān)系，則利用引理1 同樣的做法，也可以得到類似結(jié)論:

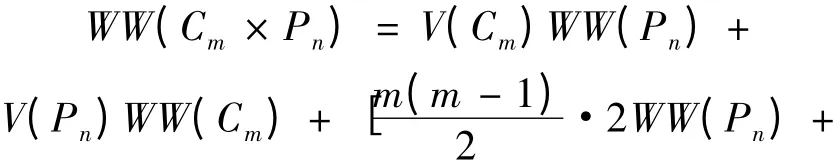
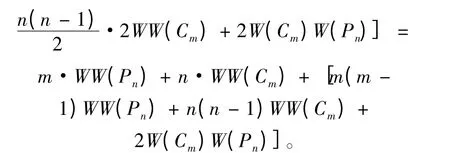
最后，考慮將結(jié)論推廣到任意兩個(gè)圖G 和H 的直積圖G × H，根據(jù)其圖中任意兩點(diǎn)距離的關(guān)系和hyper-Wiener 指標(biāo)的定義可以得到:

定理2 設(shè)G 和H 是頂點(diǎn)數(shù)分別為| V(G)| = m，| V(H)| =n 的連通圖，則有:

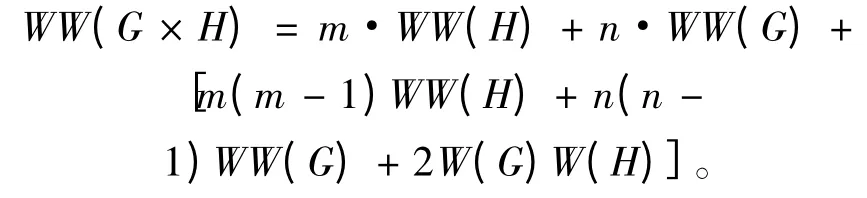
證 由性質(zhì)1 G 和H 的乘積圖G ×H 的結(jié)構(gòu)得到圖上任意兩點(diǎn)間距離滿足下面的關(guān)系式:

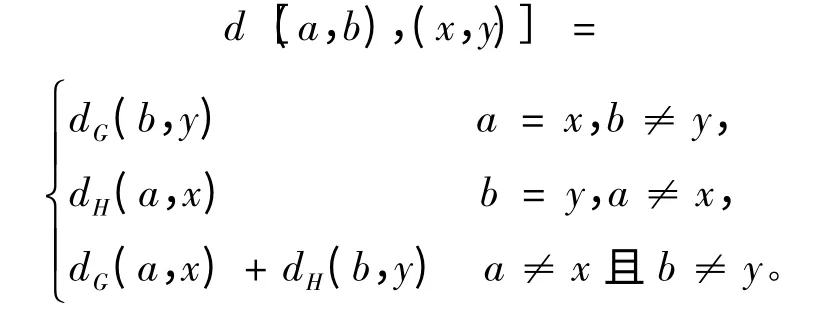
由此可見，其具有引理1 中路與路的直積圖的類似結(jié)構(gòu)性質(zhì)，所以考慮將引理1 的結(jié)論推廣到任意兩個(gè)圖G 和H 的直積圖G ×H。根據(jù)上述直積圖任意兩點(diǎn)距離的關(guān)系和hyper-Wiener 指標(biāo)的定義可以得到

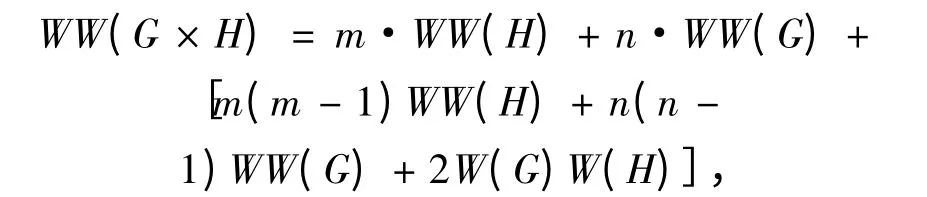
證畢。

這樣，就可以通過已經(jīng)研究出的圖類(如路圖，樹圖，單圈圖，雙圈圖)的Wiener 指標(biāo)，和hyper-Wiener 指標(biāo)［8］計(jì)算其乘積圖的hyper-Wiener 指標(biāo)。

［1］Cash G G.Polynomial expressions for the hyper-Wiener index of extended hydrocarbon networks［J］. Comput Chem，2001，25:577-582.

［2］Wiener H.Structural determination of paraffin boiling points［J］.J Amer Chem Soc，1947，69:17-20.

［3］DENG H. On the extremal Wiener polarity index of chemical trees［J］. MATCH Commun Math Comput Chem，2011，66:305-314.

［4］Klein D J，Lukovits I.On the definition of the hyper-Wiener index for cycle-containing structures［J］.J Chem Inf Comput Sci，1995，35:50-52.

［5］Gutman I.Relation between hyper-Wiener and Wiener index［J］.Chem Phys Lett，2002，364:352-356.

［6］ZHOU Bo，Gutman I.Relations between Wiener，hyper-Wiener and Zagreb indices［J］.Chem Phys Lett，2004，394:93-95.

［7］Fath-Tabar G H，Ashrafi A R. The hyper-Wiener polynomial of graphs［J］. Iranian Journal of Mathematical Sciences and Informatics，2011，6(2):67-74.

［8］XING Rundan，ZHOU Bo，QI Xuli.Hyper-Wiener index of unicyclic graphs［J］.MATCH Commun Math Comput Chem，2011，66:315-328.