一種基于KNMF的非線性故障診斷方法

冉永清 楊煜普 屈衛東

(上海交通大學電子信息與電氣工程學院自動化系系統控制與信息處理教育部重點實驗室，上海 200240)

隨著工業過程控制系統的復雜化和智能化，工業過程產生的數據維數越來越高，非線性增強，傳統的基于數據驅動的線性方法(如PCA)的故障檢測方法表現明顯不如非線性故障檢測方法(如KPCA[1,2])。這些方法在過程檢測時提取全局信息表征數據特征，然而在一些情況下，數據的局部信息具有更好的表現性能，比如部分數據丟失時，采用局部信息表示數據具有更好的魯棒性。非負矩陣分解(NMF)是近幾年發展起來針對非負數據處理的多元統計分析方法[3]，具有天然的稀疏性，能夠很好地提取數據的局部特征。但是由于NMF方法在處理非線性數據方面具有明顯不足，因此筆者引進核非負矩陣分解方法(KNMF)[4]，結合NMF方法的特點和核方法的優點，建立在線故障診斷模型，克服了線性方法處理非線性數據性能低的不足，同時解決了傳統核方法表現性能不佳、內存消耗大的問題，實現高效和準確的故障診斷。

1 核非負矩陣分解①

1.1 算法描述

KNMF通過核函數將非線性輸入空間的數據映射到線性特征空間，在特征空間內，運用NMF進行特征提取和分析。令輸入空間的數據X=[X1,X2,…,Xn]∈Rm×n，通過映射函數Φ(·):Rm→F將數據映射到一個高維的特征空間F內，令特征空間數據矩陣Φ(X)=[Φ(x1),Φ(x2),…,Φ(xn)]∈Rd×n，在特征空間F內進行NMF分解，即尋找一個基矩陣U和一個系數矩陣V，使得：

Φ(X)≈UVT

(1)

其中U∈Rd×r，d的數值非常大，r表示降維后的維數；V∈Rn×r。

假設基矩陣U的每一列滿足下列等式：

uj=Φ(x1)W1j+Φ(x2)W2j+…+Φ(xn)Wnj

(2)

則基矩陣U是特征數據Φ(X)的凸組合，即：

U=Φ(X)W

(3)

其中W∈Rn×r，并且W的每一列之和等于1。

在特征空間F中，把特征數據分解成如下形式：

Φ(X)≈Φ(X)WVT

(4)

將原NMF分解算法需要找到基矩陣U和系數矩陣V，轉化成尋找參數矩陣W和系數矩陣V。

在特征空間內，采用歐式距離來度量特征數據矩陣Φ(X)與Φ(X)、參數矩陣W、系數矩陣V三者乘積之間的誤差，將KNMF問題轉化為求取參數矩陣W和系數矩陣V，并使以下目標函數取得最小值：

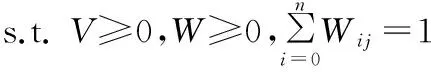
(5)

其中K為核矩陣，K=Φ(X)TΦ(X)。

對于上述目標函數，分別以W或V為變量的最小化問題的時候是凸函數，但是同時以W和V為變量是非凸函數，因此要找到兩個優化問題的全局最優解是不可能的，只能給出局部最優解。

[KWVTV-KV]⊙W=0

(6)

[VWTKW-KW]⊙V=0

(7)

根據式(6)、(7)得出參數矩陣W和系數矩陣V的更新規則：

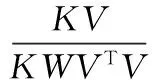
(8)

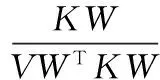
(9)

1.2 幾何意義

KNMF算法的目標是在特征空間內尋找一個凸包盡可能地把所有數據都包含在內，那么就可以根據凸包性質，所有在凸包內的點都可以通過所有凸包邊界的一個凸組合表示，故KNMF算法訓練的目標就是尋找到特征空間數據內的所有凸包邊界點，即特征數據點，構成這個凸包。特征空間內的數據點和特征數據點如圖1所示。

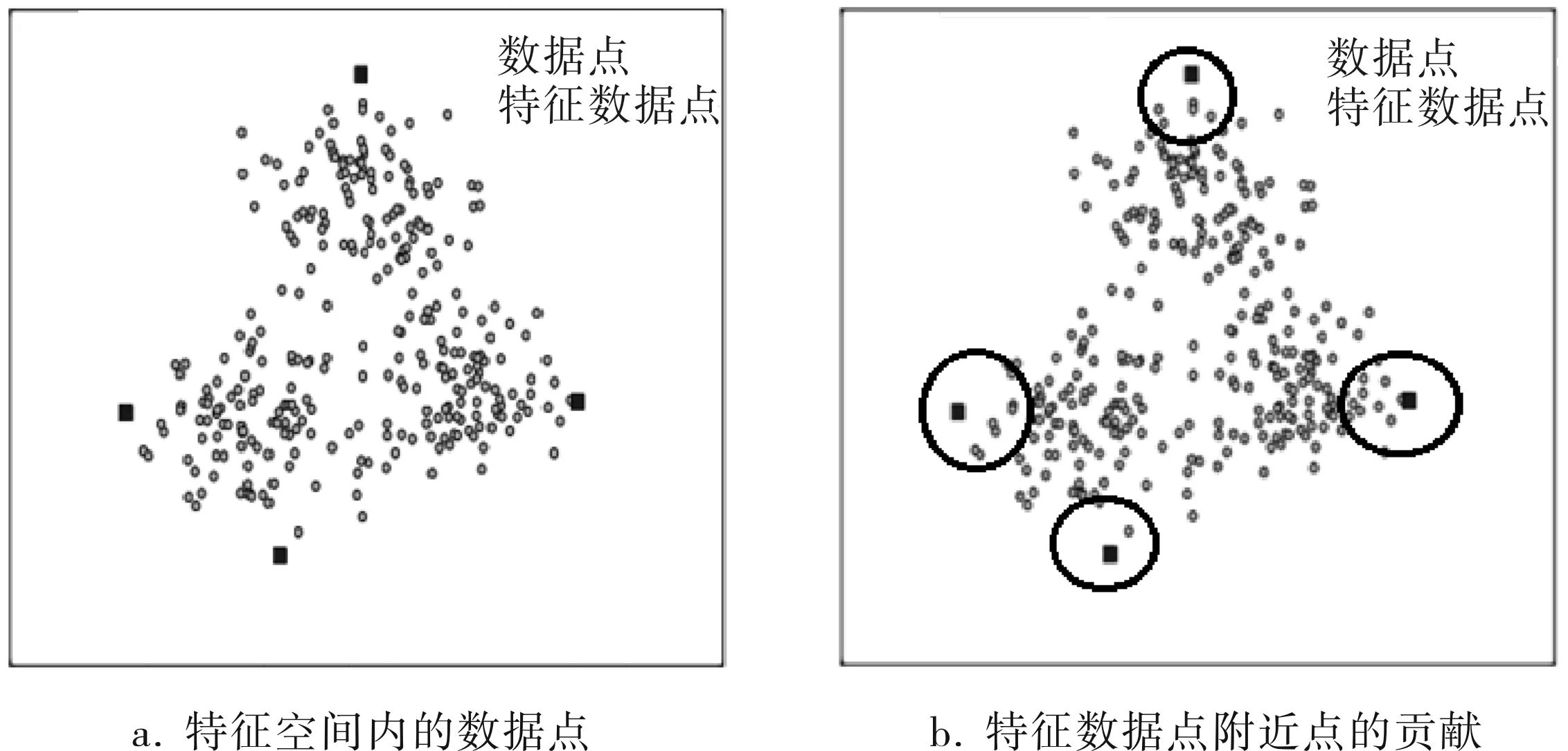
圖1 特征空間內的數據點和特征數據點

從式(3)得出，基矩陣U是特征數據Φ(X)的一個凸組合，展開式(3)，得到：

(10)

其中參數矩陣W的每一列之和為1。尋找的凸包能夠包含所有的特征數據點，并且每一個特征數據點是所有數據點的一個凸組合，所以離特征數據點越近的點，對于構成特征數據點的影響就越大，那么對應參數矩陣W中的數值就越大。在圖1b中圓圈內的點對構成特征數據點的系數影響最大，在參數矩陣W中數值相對較大。這個性質使得訓練出來的參數矩陣W具有很好的稀疏性[5]，即在矩陣中有很多元素都是0，只有少數元素不是0。

2 基于KNMF的故障檢測模型

首先獲取實際工況中產生的正常數據Y,Y∈Rm×n，其中m為變量個數，n為采樣點數。由于每一個變量的量綱不同，先對數據做標準化處理，設處理后的數據為X,X∈Rm×n，對X運用KNMF算法進行訓練，得到參數矩陣W和系數矩陣V。當用于在線檢測時，設某一次的采樣數據為x,x∈Rm，則：

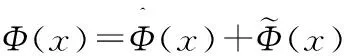
(11)

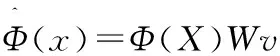
(12)

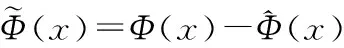
(13)

其中式(12)中的v為對應采樣數據的重構系數，即：

v=(WTKW)-1WTKx

K=Φ(X)TΦ(X)

(14)

Kx=Φ(X)TΦ(x)

式(12)表示特征數據在主空間的投影，式(13)表示特征數據在殘差空間的投影。

根據式(12)、(13)定義兩個統計量K2和SPE，分別為：

K2=vTv

(15)

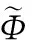
(16)

在特征空間F內，K2反映了訓練得到的模型空間內的能量波動情況，SPE反映一個測量數據到模型空間的距離，反映測量值的偏離程度。

由于構造的統計量不滿足高斯過程數據特征，所以不能運用常用方法確定其控制限，筆者采用核密度估計方法[6]，并選取了99%的置信水平確定控制限。

3 基于KNMF的故障辨識

將上述基于KNMF的故障檢測模型運用到實際工況中進行在線檢測，當檢測計算結果小于控制限時，認為過程是正常狀態，當超過控制限時，認為過程是故障狀態。當過程發生故障的時候，需要快速并準確地找到故障所在，確定故障變量，從而可以快速排除故障，避免故障帶來的災難。

當運用K2統計量和SPE統計量檢測到故障時，筆者采用貢獻圖[7]的方式，確定故障變量。對應K2和SPE每一個變量所做貢獻值的計算如下：

(17)

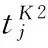
(18)

其中，下標j表示第j個變量，j=1,2,…,m；δj表示m×m單位矩陣的第j列。

通過式(17)、(18)可以確定發生故障時每一個變量對于此次故障的貢獻值，變量貢獻值越大越有可能發生故障，那么就越有可能就是故障發生的位置所在，在排除故障時，應該首先檢查此位置。

4 仿真實驗

TE過程是基于實際工業過程的仿真案例[7]。它由連續攪拌式反應釜及氣液分離塔等多個設備組成。訓練集包含500個樣本數據，測試集由前160個正常數據和后800個故障數據構成。圖2是TE過程結構圖，表1是KNMF算法與傳統算法故障檢測率的比較。

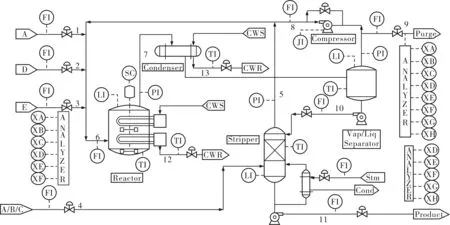
圖2 TE過程結構

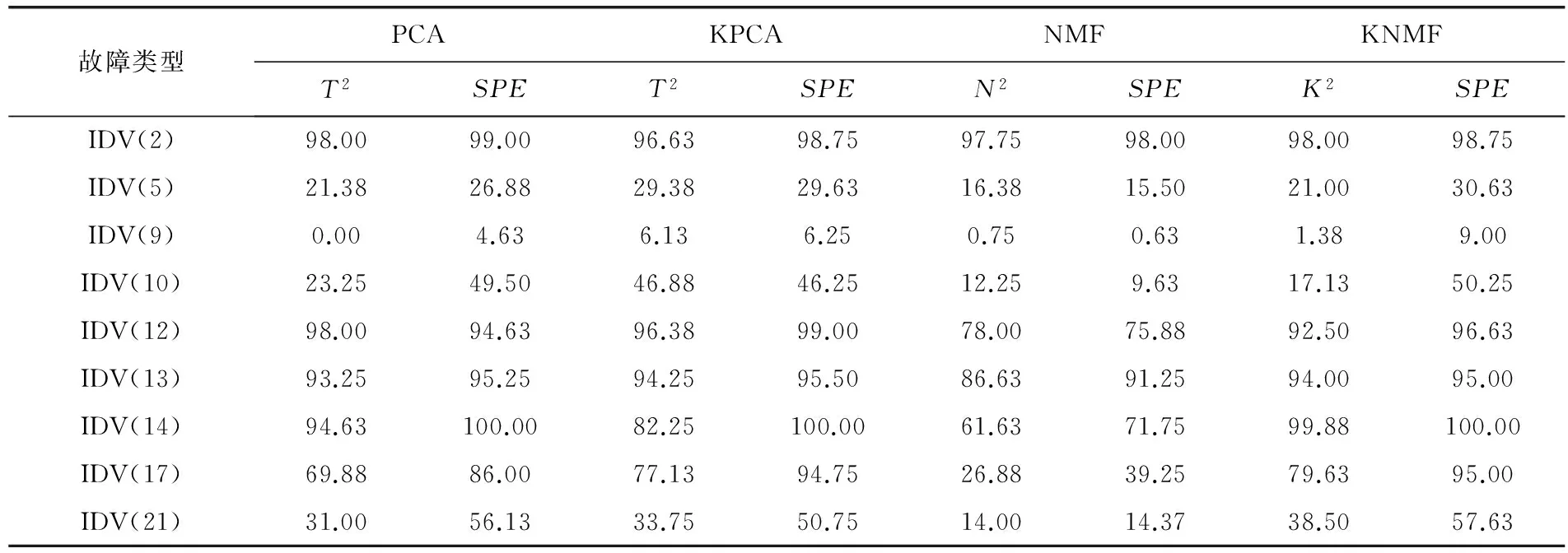
表1 KNMF算法與PCA、KPCA和NMF的故障檢測率比較 %

從表1可以看出，基于核方法(KPCA和KNMF)的檢測效果在某些故障檢測方面優于線性方法(PCA和NMF)，而KNMF方法與KPCA方法在故障檢測方面各有優勢。

圖3給出了故障IDV(14)各個方法的故障檢測圖。

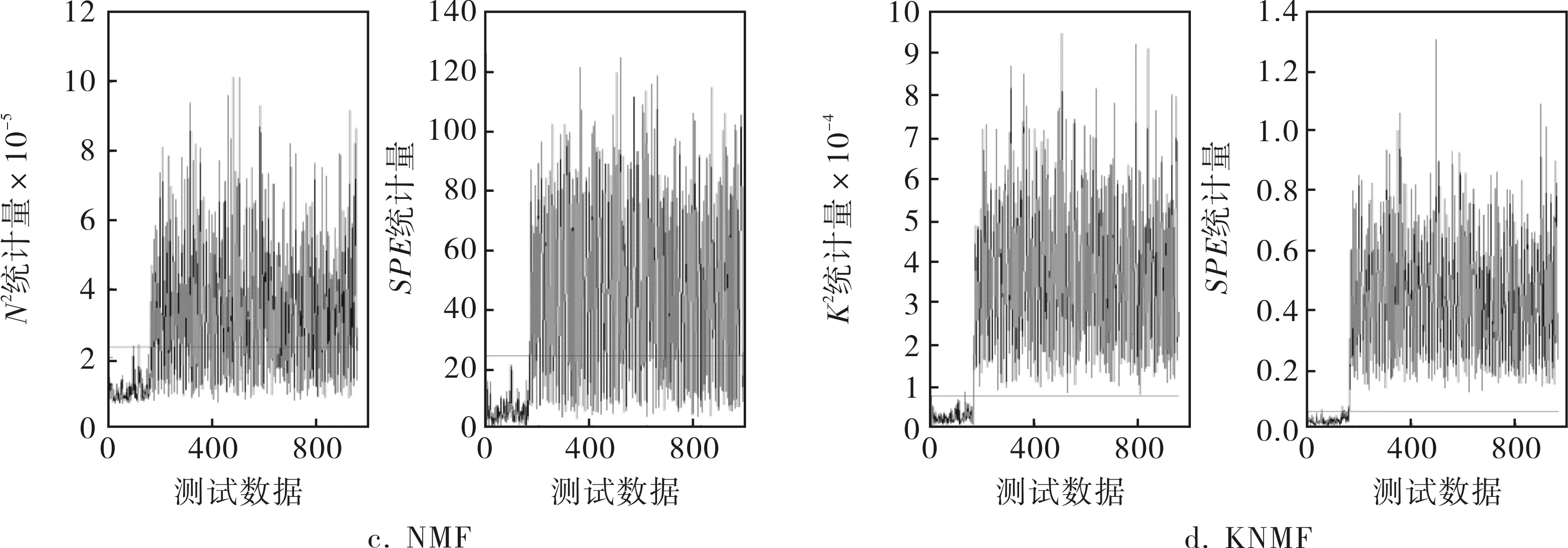
圖3 故障IDV(14)發生時，KNMF與PCA、KPCA和NMF的檢測率對比

IDV(14)表示的是反應器冷卻水閥門的變化情況，當故障IDV(14)發生時，那些與反應器相關的變量都會產生影響，如反應器中的溫度(變量9)、冷卻水的流速(變量32)和反應器冷卻水出口溫度(變量21)。當故障IDV(14)發生的時候，各個變量的貢獻值如圖4所示。從貢獻圖來看，這3個變量的貢獻值明顯很大，而其他變量貢獻值相比之下基本可以忽略，這與分析結果完全相符，這就驗證了該方法的有效性。

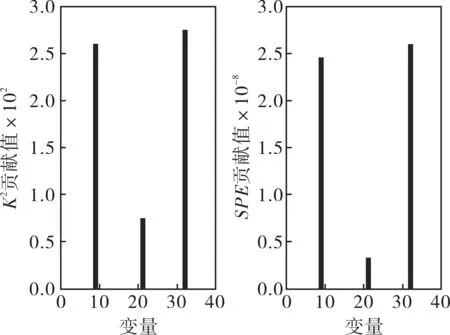
圖4 IDV(14)發生時，受影響的主要變量和所有變量的貢獻值

5 結束語

筆者提出的基于核非負矩陣分解方法(KNMF)的故障檢測方法，解決了傳統方法處理非線性方法的不足，同時得到的W或V具有天然稀疏性，減少內存消耗，克服了其他核方法消耗內存大的不足，在一定程度上能夠加快運算速度。設計了監控統計量K2和SPE，適用于在線故障檢測，并且建立了完整的故障診斷模型。當檢測到故障的同時，給出可能引起此故障的變量。最后將KNMF算法運用于TE平臺進行仿真，仿真結果表明了基于KNMF的方法在故障檢測方面的可行性和有效性。在今后的工作中，可進一步完善故障診斷模型，提高故障檢測速度和精度，提高故障辨識的準確性。

[1] Fan L P,Yu H B,Yuan D C.Monitoring of SBR Process Using Kernel Principal Component Analysis[J].Chinese Journal of Scientific Instrument,2006,27(3):249～253.

[2] 范玉剛，李平，宋執環.基于特征樣本的KPCA在故障診斷中的應用[J].控制與決策,2005,20(12):1415～1418,1422.

[3] An S, Yun J M, Choi S. Multiple Kernel Nonnegative Matrix Factorization[C].2011 IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP).Prague：IEEE,2011:1976～1979.

[4] Lee H,Cichocki A,Choi S.Kernel Nonnegative Matrix Factorization for Spectral EEG Feature Extraction[J].Neurocomputing,2009,72(13):3182～3190.

[5] Hoyer P O.Non-negative Matrix Factorization with Sparseness Constraints[J].The Journal of Machine Learning Research,2004,5:1457～1469.

[6] Botev Z I,Kroese D P.The Generalized cross Entropy Method, with Applications to Probability Density Estimation[J].Methodology and Computing in Applied Probability,2011,13(1):1～27.

[7] Yoon S,MacGregor J F.Fault Diagnosis with Multivariate Statistical Models Part I: Using Steady State Fault Signatures[J].Journal of Process Control,2001,11(4):387～400.