淺談數學期望與經濟決策的關系及其應用

劉迪佳

（渤海大學數理學院，遼寧 錦州 121000）

0 引言

任何一個學科或領域的發展都離不開數學這一重要工具的支持。改革開放以來，我國經濟取得了高速發展，社會各個領域都取得了長足進步。在此過程中，數學在經濟領域的地位越來越重要，所發揮出的作用也愈來愈大。在經濟活動中，能夠作出科學而高效的決策，與數學是密不可分的，這其中數學期望值就發揮出了重要的作用。基于此，本文即對數學期望值與經濟決策的關系作一簡單分析，并從實際例子出發，闡述了數學期望在經濟決策中的應用過程。

1 數學期望的概念

概率論是數學的重要組成部分，它通過對事物的數量關系進行分析來掌握事物的變化規律。數學期望是概率論中的概念，又稱均值或數學期望值。在概率論中，通過求解隨機變量分布函數，來從統計上描述隨機變量的變化特征。如離散型隨機變量的期望值為每次試驗中隨機變量的出現概率及其結果的綜合。數學期望反映的是隨機變量的數學特征，它代表的是隨機變量在總體取值中的平均水平。根據隨機變量的取值規律，數學期望分為了連續性和離散型兩種。

1.1 連續型

如果隨機變量X的分布函數F（x）可表示成一個非負可積函數f（x）的積分，則稱X為連續型隨機變量。若隨機變量X的概率密度為函數F（x），且有 絕對收斂，則將這個積分值稱為X的數學期望。

1.2 離散型

如果隨機變量的取值是有限個或至多可列個值，則這個變量稱為離散型隨機變量。若離散型隨機變量X的取值為xi時的概率為pi，且其積的和是絕對收斂的，那么這個隨機變量的數學期望即為E（X）=。

如果對象是隨機變量函數，即隨機變量是ε，為離散型隨機變量，η=g（ε）為隨機變量函數，且為連續實函數，其概率值的分布為p（ε=xi）=pi（i=1，2，3......），若存在絕對收斂級數 ，則將這個級數成為隨機變量函數 η =g（ε）的數學期望，記為 。

2 數學期望與經濟決策的關系

2.1 數學期望為經濟決策提供了工具

作為經濟活動主體的企業，在其從事的各項經濟活動的過程中，常常需要企業管理者在各類條件和選擇中作出決策，對于一些簡單問題，僅僅需要企業管理者憑借經驗或企業的經營情況來確定決策。

但在面對一些復雜的情況時，卻需要企業管理者基于大量的數據來進行縝密的分析和研究后作出決策，而數學期望則可以為企業的管理者提供數學分析的工具，來幫助企業計算數據進而得出答案，幫助管理者作出相應的決策。

2.2 數學期望提高了經濟決策的效率

企業管理者在管理企業的過程中，大多數時候所面對的是復雜的問題，需要管理者對企業的宏觀經營情況和微觀情況進行了解和把握，不僅需要耗費大量的時間，而且也需要管理者投入較多的精力去思考和判斷，這就使得在一些決策確定后已經耽誤了市場先機，使企業陷入被動。

而將數學期望的方法引入到企業的決策中來，則能夠通過數學計算，甚至計算機輔助工具，高效地得出數學運算結果，進而幫助企業管理者確定方案，極大地提高了決策的效率。

2.3 數學期望促進了經濟決策的科學性

知識來源于人類的實踐活動，是人類對事物規律的科學認識，而反過來通過在實踐中運用知識，又能能動地改造客觀的世界，對于數學學科來說，其最大的價值就是運用事物的規律來幫助人們提高實踐活動的科學性。

在現實生活中，企業管理者常常是在感性思考和分析的基礎上作出決策，這就使得一些決策在執行的時候，往往出現很多的不合理性，由此導致決策失誤，影響企業的正常運營，而將數學期望的方法引入到決策的過程之中，則可以使企業管理者基于嚴謹的數學運算的基礎上，得出科學、準確的結果，進而依據計算結果做出相應的決策，大大地實現了科學決策、理性決策。

3 數學期望在經濟決策中的應用步驟

將數學期望在經濟決策中的應用通常需要經過以下幾個步驟：

第一，確定要決策的目標。將需要分析得出的目標結果選定，進而綜合各方面的因素，在相關條件的約束下，選定出多種可行的備選方案。

第二，分析因素，計算概率。對各個備選方案中可能對目標結果產生影響的可控性因素和不可控因素進行全面分析，將不可控因素進行羅列，而后通過數學方法來計算各種不可控因素的出現概率。

第三，預測收益值。在得出各個不可控人為因素概率的基礎上，運用統計方法來預測各個備選方案在實際的環境中可能取得的收益值，并將收益值和相應的概率進行對應、列表，進而得出基于預測收益值和概率值的直觀收益矩陣表。

第四，計算期望，確定最佳方案。以直觀的收益矩陣表為數據基礎，運用數學期望的計算公式分別計算各方案的期望收益值，進而通過比較計算得出的結果來確定最佳的決策方案，并在經濟活動中依照最佳的決策方案執行。

4 數學期望在經濟決策中應用的案例

在實際的經濟活動中，數學期望值與經濟決策有著諸多聯系，如上文所述，數學期望值的求解不僅為經濟決策提供了方法和參考的工具，更提高了經濟決策的效率、促進了經濟決策的科學性。例如在幫助企業制定最佳的產品生產計劃、輔助超市確定最優的貨品進貨數量、計算企業的最大化利潤等等問題中，數學期望的方法發揮出了重要的作用。下面即通過實際的例子來闡述數學期望值在經濟決策中的運用。

4.1 數學期望在企業選擇最佳生產量中的應用

在生產類型企業之中，企業經過市場調查和分析后，一般會作出多種生產方案和計劃，進而依據市場需求的未來趨勢和客戶訂單量確定企業自身的產品生產量。企業能否科學準確地確定最優的生產方案，將直接關系著企業的生產成本和經營收益。因此，企業管理者常常利用數學期望的方法來分析不同的生產方案，依據數學計算結果來比較各個方案的收益或損失，進而確定最佳生產量的方案。

例如：在某運動鞋生產企業中，企業管理者為了確定企業在未來5年內各個款式運動鞋的生產數量，以便及早地安排生產線和材料供給，企業管理者根據過去的銷售統計資料，以及企業對于未來市場的預測，得出未來企業的運動鞋實現銷量上漲、銷量穩定、銷量下滑的概率分別為0.3、0.5、0.2。如果企業將生產量分為大批量（500萬雙）、中等批量（400萬雙）、小批量（300萬雙）3個批量進行投產，則每種批量在未來5年的銷量走勢的益損值分別為：大批量（18、12、-4）；中等批量（10、15、10）；小批量（6、8、8）。 試問企業該選擇哪種生產方案？

分析求解過程：在這個案例中，對于每個生產批量總的益損值我們未知，但可以通過求解數學期望的方法求得，為此，可以設大批量、中等批量和小批量的益損值分別為x1，x2，x3，則其數學期望分別為：E（x1）=10.6，E（x2）=12.5，E（x3）=7.4，通過對三種生產批量的期望值進行比較可以得出，企業選擇中批量進行投產最為科學。

4.2 數學期望在超市確定最優庫存量中的應用

某超市在國慶期間要上架一款進口的應季水果，現該款水果的進貨價為65元/kg，超市的售價為70元/kg，根據超市的銷售規則，如果該款水果供大于求，則容易導致水果過期，需要及時削價20%進行處理；如果該款水果銷售出現供不應求現象，則超市將會被處以10元/kg的罰款。現已知消費者對于該款水果的購買需求量為X，其在[20000，80000]這一區間服從均勻分布，試問，在國慶期間，超市應該如何確定該款水果的庫存量，以實現銷售利潤的最大化？

分析求解過程：從該案例可以得知，求解的對象為超市對于該款水果的庫存量，可以設庫存量為M，消費則的需求量為X，則超市的利潤函數為：

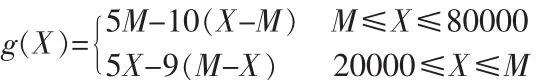
需求量X的密度函數為：

由此可得期望利潤為：

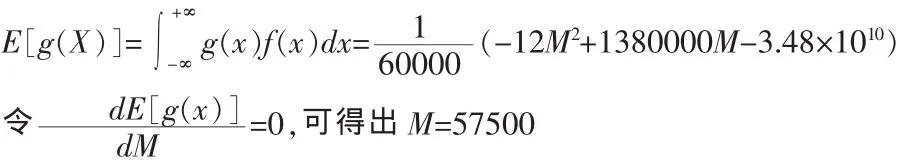
由此，當超市的該款水果庫存量為57500kg時，超市將獲得最大期望利潤。

5 結語

數學期望的方法在經濟決策中還有很多的應用，隨著經濟的發展，越來越多的經濟活動將需要借助數學工具來求解最優化的結果，但需要注意的是，通過數學期望的方法來求得的結果應當作為企業管理者進行決策的一項參考，在實際的經濟活動中，企業管理者仍應當綜合考慮市場競爭、政策變化等多種因素，只有在辯證且全面地權衡利弊之后，才能作出有利于企業發展的決策。

［1］熊建華.概率論在幾個經濟生活問題上的應用[J].價值工程,2014(35).

［2］拉窮.數學期望在經濟學中的簡便應用[J].價值工程,2014(35).

［3］姚明方.數學在經濟預測及決策中的重要性及其運用[J].才智,2014(25).