高速平面并聯機器人動態分析與實驗*

高名旺，張憲民（.山東理工大學機械工程學院 淄博，55049）（.華南理工大學機械與汽車工程學院 廣州，5064）

高速平面并聯機器人動態分析與實驗*

高名旺1，張憲民2
（1.山東理工大學機械工程學院 淄博，255049）
（2.華南理工大學機械與汽車工程學院 廣州，510641）

基于彈性動力學和實驗對高速輕型平面并聯機器人的動態響應進行研究。首先，根據機構的幾何和慣性非線性建立機構運動微分方程組，對機構的兩個典型位形的動態響應進行分析；其次，建立了由3-RRR輕型并聯機構和控制系統組成的實驗裝置，對理論分析進行了驗證。結果表明，在位形2，理論分析和實驗一致，即機構的殘余振動很快衰減；在位形1，理論分析與實驗兩者不同，實驗測量的動態響應為自激振動，而數值仿真得到衰減的殘余振動。同時，結果也表明機構在不同位形有不同的動態響應。

平面并聯機器人；高速；彈性動力學；殘余振動

引 言

和串聯機構相比，并聯機構具有高定位精度、更高的加速度和負載能力等［1］優點，因而應用廣泛；然而并聯機構在工作空間的動態特性非常復雜［2］，這給機構的設計和使用造成很大困難。輕量化的并聯機器人在高速、高加速工作時，桿件的彈性變形容易導致系統整體彈性振動，從而影響機構的應用。彈性動力學廣泛用于模擬串聯機器人和四桿機構［3］，也逐漸用于并聯機構分析。文獻［4］利用虛功原理對柔性五桿機構建立動力學模型并實驗驗證。Zhou等［5］運用有限元法建立柔性3-PRS機構的動力學公式并分析其振動特性。Wang等［6］和Zhang等［7］分別運用有限元法和假定模態法對3-PRR機構建立動力學模型，并對其進行了主動振動控制研究。劉善增等［8］對3-RRC并聯機器人建模分析其動態特性。Zhao等［9］運用有限元方法模擬分析六自由度并聯機器人的動態特性。Rognant等［10］提出一種建立并聯機構彈性動力學模型的步驟。然而，以上研究在不同位形、高速運動對并聯機構動態特性影響的分析，尤其是實驗研究相對較少［11］。

筆者基于有限元法建立3-RRR機構的彈性動力學模型，在工作空間內對不同位形的動態特性進行研究。首先，利用彈性動力學模型對機構的兩個典型位形的動態特性進行分析；然后，利用實驗裝置對兩個典型位形的動態特性進行測試。結果表明，在位形2位置，仿真結果和實驗結果一致，而位形1的仿真結果和實驗結果有較大差異。該研究結果為機器人的運動規劃和控制提供參考。

1 3-RRR機構彈性動力學模型

如圖1所示，3-RRR平面并聯機器人由動平臺、靜平臺和鏈接兩者的支鏈組成。支鏈由鉸和連桿組成，其中：鉸包含主動鉸Oi、被動鉸Bi和Ci；連桿分別為主動桿OiBi和被動桿BiCi。假設連桿為柔性桿，其余元件為剛性體。慣性坐標系O-xy建立在靜平臺上，坐標系原點在三角形O1O2O3的形心，z軸按右手螺旋確定。

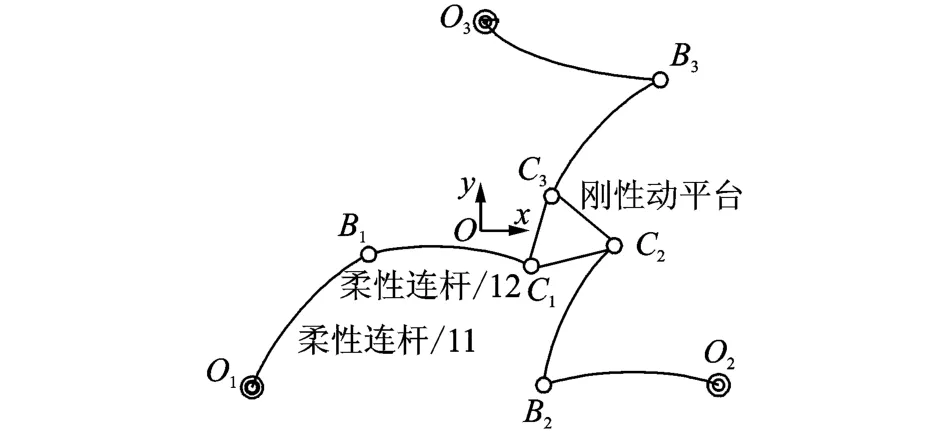
圖1 3-RRR機構Fig.1 3-RRR mechanism

1.1 單元位移

柔性連桿的運動用等效剛體模型描述［12］。平面梁單元如圖2所示。實線部分為彈性變形單元，虛線部分為假設的剛體未變形單元。單元坐標系為a-xy，x軸為剛體單元中性軸方向，原點在剛體單元的端點a。

彈性體的橫向變形采用三次Hermit多項式［13］，軸向彈性位移采用線性插值函數。彈性體中任意一點的彈性位移在單元坐標系中可表示為

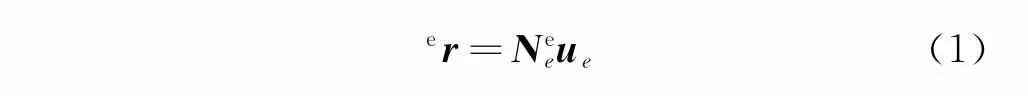
其中：ue為梁單元位移向量；Ne為梁單元形函數；r為彈性體中C點相對瞬態剛體運動的彈性位移向量，式中向量左上標e表示在單元坐標系中表示。

位置向量可寫成如下形式

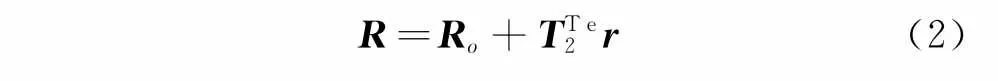
其中：Ro為C點在剛性單元中對應的點的坐標向量；T2為慣性坐標系到單元坐標系的2×2矩陣。對式（2）兩邊求導可得C點速度

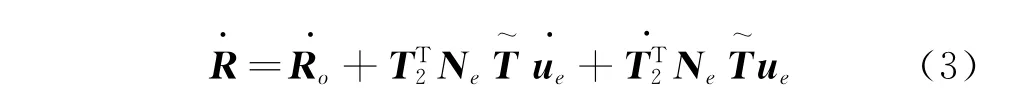
其中：T為慣性坐標系聯系單元坐標系的6×6常數矩陣；T～

表示公式求導。

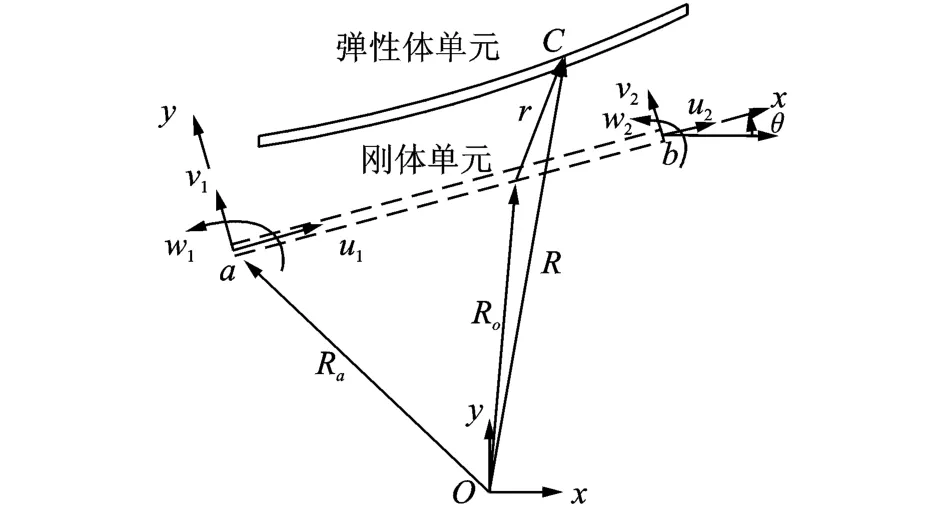
圖2 歐拉-伯努利單元Fig.2 Euler-Bernoulli element

1.2 支鏈的動能和勢能

支鏈中的連桿由3部分組成，即連桿兩端的集中質量和中間的柔性桿。筆者把柔性桿作為一個柔性單元，連桿兩端集中質量的動能分別合并到動平臺和被動鉸Bi單元的動能中。支鏈的動能為

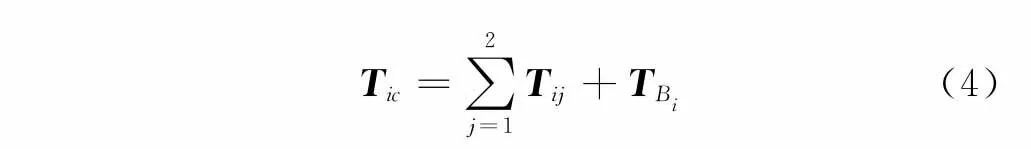
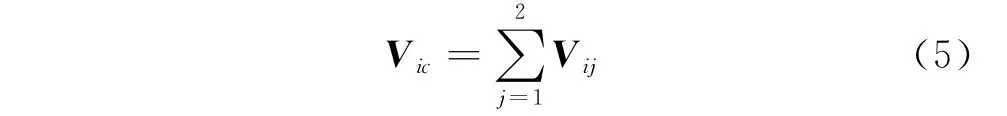
其中：Vij為第i支鏈第j連桿的勢能。

1.3 全局坐標

系統的全局坐標如圖3所示，總共取18個節點坐標。系統全局坐標可表示為

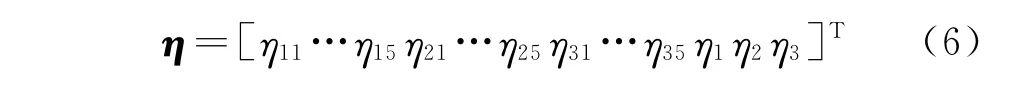
其中：Tic為第i支鏈的動能；Tij為第i支鏈第j連桿的動能；TBi為第i支鏈被動鉸Bi的動能。

支鏈的勢能為

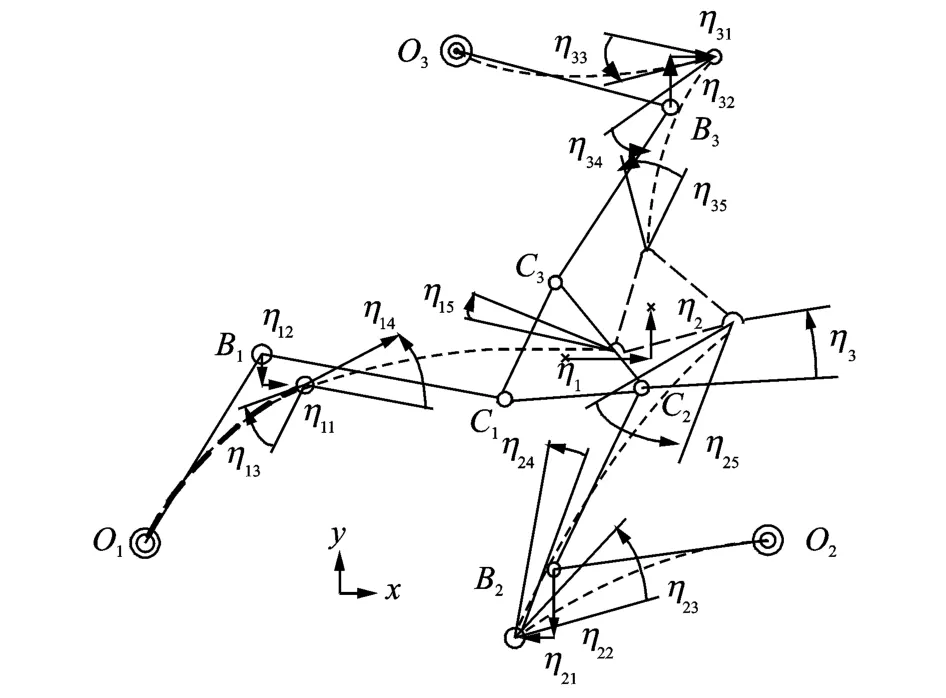
圖3 全局坐標Fig.3 Global coordinate

單元位移向量和全局坐標的映射由連接矩陣Si1，Si2，SBi和Sp實現。

單元i1的位移向量與全局坐標的關系為

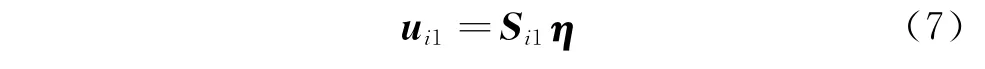
單元i2的位移向量與全局坐標的關系為

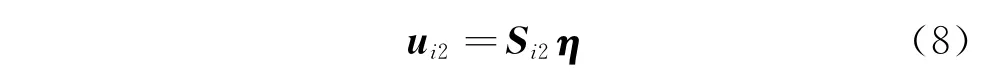
單元Bi的位移向量與全局坐標的關系為

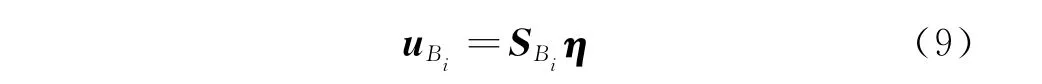
動平臺的位移向量和全局坐標的關系為

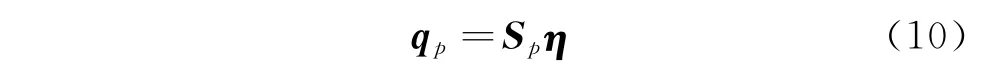
1.4 系統動力學模型

1.4.1 動力學模型

考慮剛體運動對彈性振動的影響，因而機構的拉格朗日等式可用系統的柔性全局坐標表示，則3-RRR機構的運動等式為

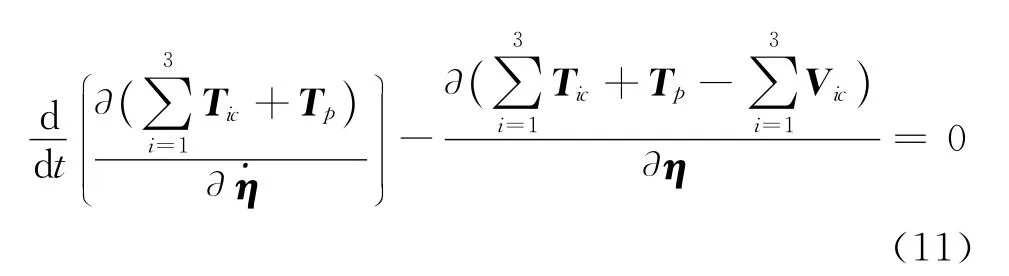
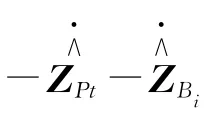
1.4.2 增加比例阻尼的系統動力學模型

通常在有限元分析中，使用比例阻尼模擬結構阻尼，比例阻尼是質量矩陣和剛度矩陣的線性組

其中：Tp為動平臺的動能。

把式（4），（5），（7）～（10）分別代入式（11），整理并寫成矩陣形式為合［14］，即增加比例阻尼后動力學模型可表示為

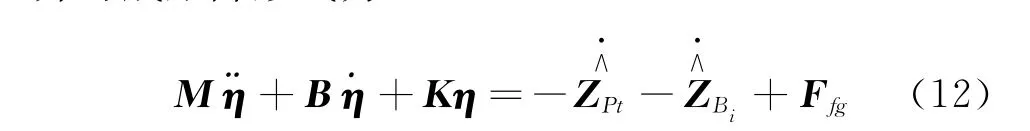
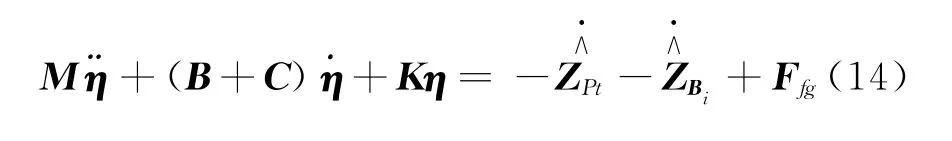
2 數值仿真

為研究機構在工作空間不同位形的動態特性，以機構的兩個典型位形為例進行運動響應研究。利用彈性動力學模型對機構在典型位形的動態響應進行仿真分析。并聯機構的桿件采用鋁合金，材料彈性模量為0.7×105MPa，材料密度為2.7×103kg/m3，主要參數如表1所示。

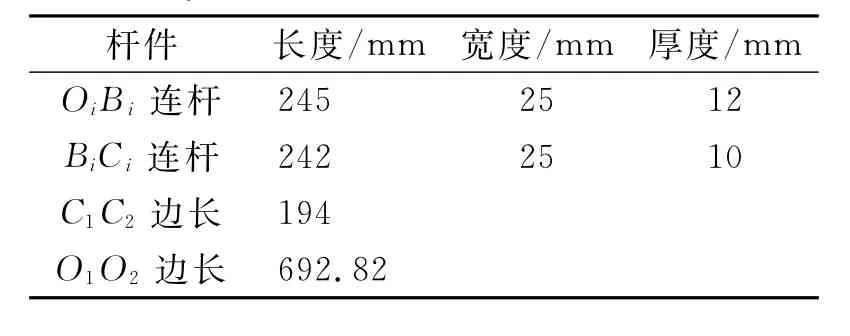
表1 機構連桿參數Tab.1 Parameters of mechanism link

2.1 位形1的殘余振動仿真分析

位形1（0.15 m，0）如圖4所示。機構以梯形速度規劃從原點移動到點（0.15 m，0），其加速度為20 m/s2，速度為1 m/s。此位移被稱為軌跡1，具體位移規律為

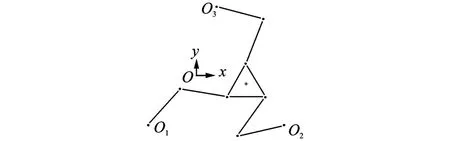
圖4 位形1Fig.4 Configuration one

其中：a為運動加速度；x，y分別表示x，y軸方向的位移規律；φ表示繞z軸的轉動規律。

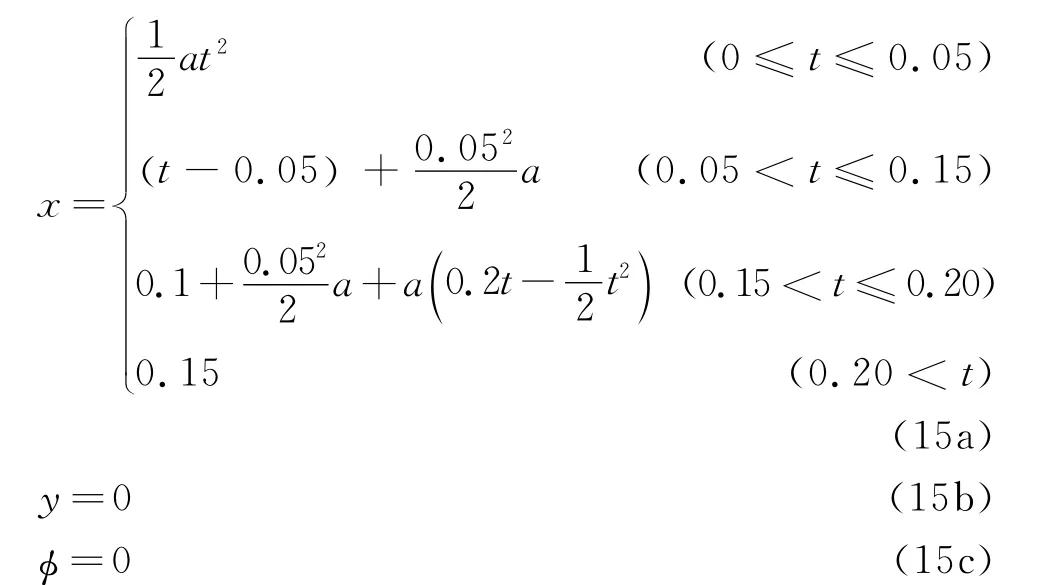
式（15）描述了機構在0.2 s內沿x軸從原點移動到點（0.15 m，0）。為更好地比較機構在位形1的動態特性，在Matlab/Simulink中編程并運行0.5 s。動平臺的動態響應如圖5和圖6所示，分別表示機構在x軸和y軸的振動位移。

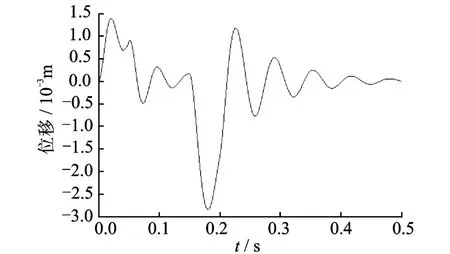
圖5 位形1的x軸振動位移Fig.5 Vibration of x direction at configuration one

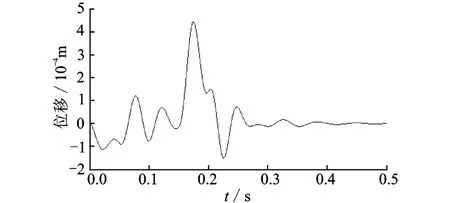
圖6 位形1的y軸振動位移Fig.6 Vibration of y direction at configuration one

由圖5可看到，在加速階段，即0≤t≤0.05 s，機構受到較大沖擊，x軸的振動幅值為1.39 mm。在勻速階段，即0.05＜t≤0.15 s，振動幅值減少。在減速階段，即0.15＜t≤0.2 s，振動幅值又增加，達到2.85 mm，此時機構的剛度變小，從而導致彈性變形增大。最后，當t＞0.20 s時，運動響應為殘余振動，其幅值為1.18 mm，并且逐漸衰減。由圖6看到，在各個階段，機構在y向的振動幅值都較小，幅值為0.44 mm，尤其是殘余振動振幅小，為0.15 mm，衰減快說明x向擾動對y方向的影響較小。

2.2 位形2的殘余振動仿真分析

位形2如圖7所示，即點（-0.15 m，0），是位形1的對稱位形。軌跡2為機構從原點沿x軸運動到點（-0.15 m，0）。機構位移規律如式（16）所示。

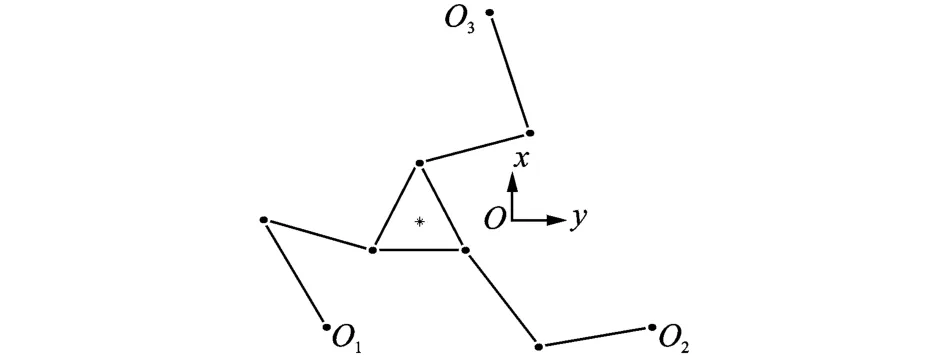
圖7 位形2Fig.7 Configuration two

式（16）描述了機構在0.2 s內沿x軸從原點移動到位形2，移動速度和加速度與前面一致。動平臺的動態響應如圖8，9所示。圖8為x軸振動位移。圖9為y軸振動位移。

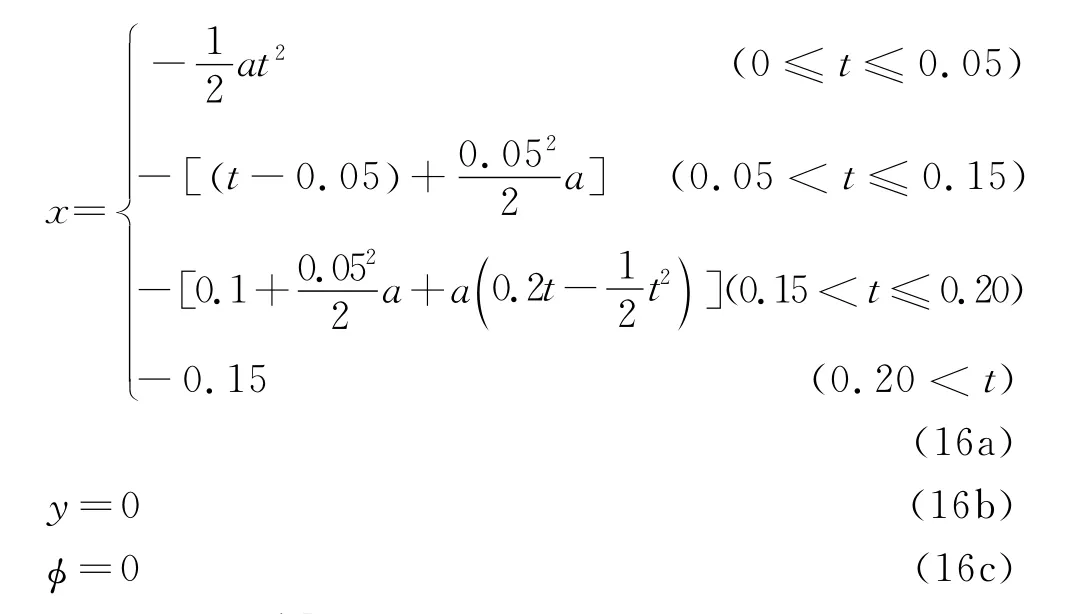
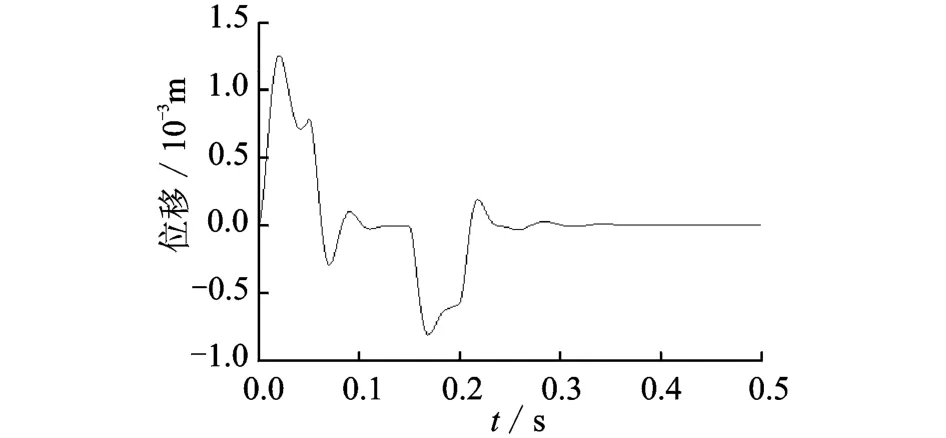
圖8 位形2的x軸振動位移Fig.8 Vibration of x direction at configuration two

從圖8可知，在加速階段，x軸的振動幅值較大，達到1.33 mm。在勻速運動階段，振動幅值減少。在減速運動時，幅值為0.81 mm，比加速階段的幅值小。最后，運動到達指定點后，即t＞0.20 s時，機構的殘余振動幅值僅為0.19 mm且很快衰減。

在圖9中，y軸各階段的振動幅值都較小，加速階段y向振動幅值僅為0.09 mm，說明在此階段x軸的力擾動對y軸的影響較小，同時也表明此時其y軸剛度大；在減速階段，y軸產生的振動幅值為0.73 mm，比加速時大，意味著機構在y軸的剛度變小了；最后，機構殘余振動的幅值為0.28 mm。

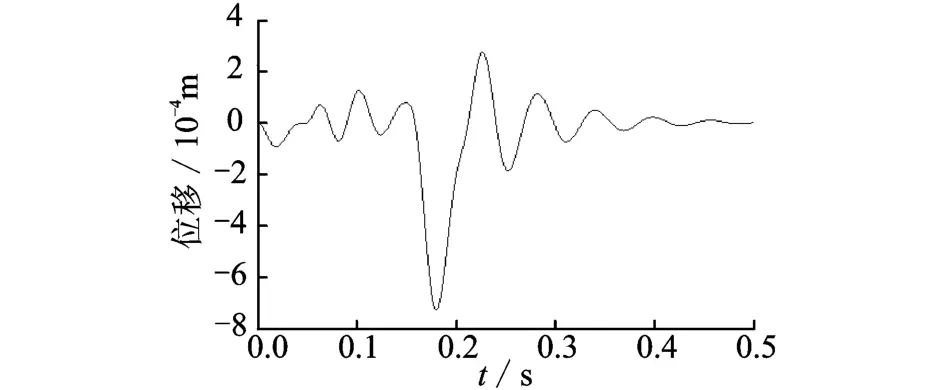
圖9 位形2的y軸振動位移Fig.9 Vibration of y direction at configuration two

圖5與圖8比較可知，位形1的殘余振動幅值比位形2的大，說明機構在位形1的剛度小，振動超調量大。圖6和圖9比較可知，不同的方向有不同幅值的殘余振動，說明機構在某一位形的不同方向的剛度也不同。

3 實 驗

3-RRR實驗設備如圖10所示，設備包含并聯機構、伺服電動機和dSPACE控制器。3-RRR機構由鋁合金制成的輕型連桿、動平臺和基座組成，連桿之間用滾動軸承連接。3個交流伺服電動機被固定在基座上，其額定轉速為3 kr/min。在Matlab/Simulink中編好程序，然后下傳到dSPACE中，通過伺服電動機控制機構運動。

機構的運動速度為1 m/s，加速度為20 m/s2。機構的動態響應用動平臺的位移表示，動平臺的位移由激光干涉儀XL-80測量得到。軌跡1的實測位移如圖11所示。可以看到，機構的殘余振動振幅由1.63 mm逐漸增大至3.57 mm，最后形成幅值固定的有規律的振動，這種振動為自激振動。這種現象和圖5的仿真結果有所不同，因為機器人發生機電耦合作用。機構在此位形的殘余振動誘發了伺服系統，伺服系統成為機構的激勵源，從而形成了自激振動。圖12為位移1的速度變化規律，該圖清楚地表明自激振動的發生和發展。

圖10 3-RRR機構照片Fig.10 Photo of the 3-RRR manipulator

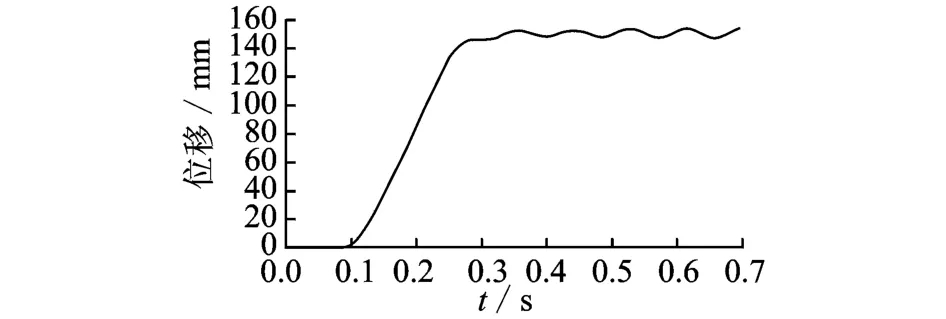
圖11 軌跡1的動態響應Fig.11 Dynamic response of trajectory one

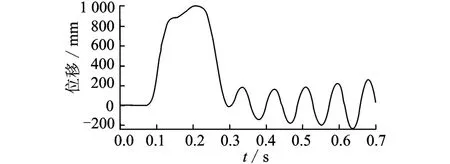
圖12 軌跡1的速度Fig.12 Velocity of trajectory one

軌跡2的實測位移如圖13所示，機構的殘余振動的幅值為0.14 mm且很快衰減。與圖10相比，振動非常小，因而機構在位形2的動態性能更好。與圖8相比，兩者的殘余振動幅值相近，相差0.05 mm。實驗證明理論模型能模擬機構的動態響應。

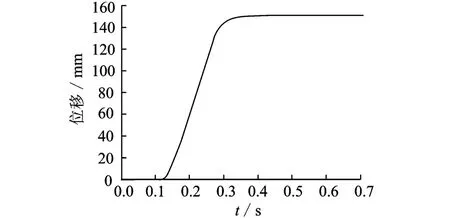
圖13 軌跡2的動態響應Fig.13 Dynamical response of trajectory two

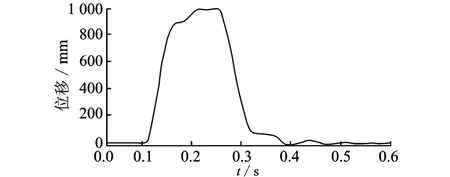
圖14 軌跡2的速度Fig.14 Velocity of trajectory two

由圖14的速度變化可以清楚地看到機構的殘余振動變化規律。圖12和圖14比較發現，機構在位形1的殘余振動較大且不斷增大，形成自激振動，在位形2的殘余振動幅值小且衰減很快。

4 結束語

動力學模型能較好地模擬機構的殘余振動，但不能正確地模擬實際機器人的自激振動。模擬和實驗表明并聯機器人在不同位形的殘余振動有很大不同。有的位形超調量大，而且會形成自激振動，有的位形超調量小，因而在應用并聯機構時要考慮在不同位形的動態響應，避免較大的位置誤差。仿真可以看出，機構在同一位形時，不同方向的動態響應也不同，因此實際應用時要考慮機構的運動方向。

［1］ Merlet J R.Parallel robots［M］.2nd ed.Netherlands：Springer，2006：20-23.

［2］ Piras G，Cleghorn W L，Mills J K.Dynamic finite-element analysis of a planar high-speed，high-precision parallel manipulator with flexible links［J］.Mechanism and Machine Theory，2005（40）：849-862.

［3］ Giovagnovi M.Dynamics of flexible closed-chain manipulator［C］∥ASME Design Technical Conference.［S.l.］：America Society of Mechanical，1992，69（2）：483-490.

［4］ Gasparetto A.On the modeling of flexible-link planar mechanisms：experimental validation of an accurate dynamic model［J］.Journal of Dynamic Systems，Measurement and Control，2004，126：365-375.

［5］ Zhou Zili，Xi J，Mechefske C K.Modeling of a fully flexible 3-PRS manipulator for vibration analysis［J］.Journal of Mechanical Design，2006，128：403-412.

［6］ Wang Xiaoyun，Mills J K.Dynamic modeling of a flexible link planar parallel platform using a substructuring approach［J］.Mechanism Machine Theory，2006，41（6）：671-687.

［7］ Zhang Xuping，Mills J K，Clehorn W L.Coupling characteristics of rigid body motion and elastic deformation of a 3-PRR parallel manipulator with flexible links［J］.Multibody System Dynamics，2009，21：167-192.

［8］ 劉善增，余躍慶，劉慶波，等.3-RRC并聯機器人動力學分析［J］.機械工程學報，2009，45（5）：220-224.Liu Shanzeng，Yu Yueqing，Liu Qingbo，et al.Dynamic analysis of 3-RRC parallel manipulator［J］.Journal of Mechanical Engineering，2009，45（5）：220-224.（in Chinese）

［9］ Zhao Yongjie.Dynamics analysis and characteristics of the 8-PSS flexible redundant parallel manipulator［J］.Robotics and Computer-Integrated Manufacturing，2011，27：918-928.

［10］Rognant M E，Courteille E，Maurine P.A systematic procedure for the elastodynamic modeling and identification of robot manipulators［J］.IEEE Transactions on Robotics，2010，26（6）：1085-1093.

［11］Yu Yueqing，Du Zhaocai，Yang Jianxin，et al.An experimental study on the dynamics of a 3-RRR flexible parallel robot［J］.IEEE Transactions on Robotics，2011，27（5）：37-46.

［12］Chang L W，Hamilton J F.The kinematics of robotic manipulators with flexible links using an equivalent rigid link system ERLS model［J］.Journal of Dynamic Systems，Measurement and Control，1991，113：48-53.

［13］Cook R D，Malkus D S，Plesha M E.Concepts and applications of finite element analysis［M］.The Unite States：Wiley，2001：75-78.

［14］Rao S S.Mechanical vibrations［M］.5th ed.Englewood Cliff：Prentice Hall，2010：431-433.

TP242；TH113

10.16450/j.cnki.issn.1004-6801.2015.04.023

高名旺，男，1973年1月生，博士、講師。主要研究方向為并聯機器人動力學與控制。曾發表《3-RRR高速并聯機器人運動學設計與實驗》（《機器人》2013年第35卷第6期）等論文。E-mail：gmw-2001@163.com

*國家自然科學基金重大研究計劃資助項目（91223201）；中央高校基本科研業務費資助項目（2012ZP0004）

2014-01-28；

2014-04-28