基于HHT的高壩泄流結構工作模態參數辨識*

張建偉，朱良歡，江 琦，趙 瑜，郭 佳（華北水利水電大學水利學院 鄭州，450011）

基于HHT的高壩泄流結構工作模態參數辨識*

張建偉，朱良歡，江 琦，趙 瑜，郭 佳
（華北水利水電大學水利學院 鄭州，450011）

基于高壩的工作特點，提出一種適用于泄流結構的工作模態參數時域辨識方法。對于低信噪比泄流結構振動信號，首先，利用小波閾值-經驗模態分解（empirical mode decomposition，簡稱EMD）聯合濾波方法濾除低頻水流脈動噪聲和高頻白噪聲，得到結構振動有效信息；然后，通過希爾伯特-黃變換（Hilbert-Huang transform，簡稱HHT）原理辨識結構系統的固有頻率及阻尼比；最后，結合奇異熵增量理論對系統模態進行定階和模態驗證。仿真研究表明，該方法能夠有效避免模態分解中的頻率混雜，具有較強的魯棒性以及較高的辨識精度。將該方法應用于三峽重力壩5號溢流壩段，可準確辨識出結構系統的工作模態參數，為研究高壩泄流結構安全運行與在線無損動態檢測提供基礎。

泄流激勵；工作模態；參數辨識；小波閾值-經驗模態分解聯合濾波；希爾伯特-黃變換

1 問題的引出

模態參數辨識是系統辨識方法在工程領域的應用。模態作為結構的固有振動特性，能夠準確預報某頻段內結構在外部或內部各種振源作用下的實際振動響應，可用于結構的健康安全檢測或優化設計等過程［1］。傳統的模態分析方法是建立在系統輸入和輸出數據已知的基礎上，利用完整的激勵和響應信息進行參數辨識。由于在實際工程中難以獲得結構完整輸入激勵信息，因此僅利用響應數據的工作模態分析技術逐漸發展起來［2］。工作模態參數辨識方法主要分為頻域辨識法和時域辨識法。頻域辨識法是將時域內測得的數據通過傅里葉變換（Fourier transform，簡稱FT）轉換到頻域內，然后由功率譜函數進行辨識。該類方法概念清晰，不易遺漏模態。時域辨識法是直接應用實測響應數據在時域內進行參數辨識，避免了頻域辨識法中由于傅里葉變換而引起的截斷誤差，提高了辨識精度［3］。工作模態參數辨識方法對比如表1所示。

隨著計算機技術、信號分析技術和試驗手段的進步，基于振動的模態參數辨識研究得到了發展。研究對象已從單一較小線性不變結構向大型多相耦合非線性動力時變體系過渡，研究方法從經典的頻域方法發展到現代時-頻聯合分析方法和人工智能方法，激勵方式由簡單的脈沖方式發展到復雜的環境隨機激勵，研究結構所處的背景環境由無干擾噪聲到強干擾、強耦合、多特征條件下的隨機噪聲［4］。章國穩等［5］提出基于特征值分解的隨機子空間算法，解決了數據驅動隨機子空間法計算效率低下的問題。文獻［6］對自然激勵技術（naturalexcitation technique，簡稱NExT）和特征系統實現算法（eigensystemrealizationalgorithm，簡稱ERA）的結合算法進行改進，并準確辨識出金門大橋的垂向和扭轉模態。文獻［7］運用Morlet小波及一個調整參數對結構自由衰減響應進行模態識別，該方法具有良好的抗環境噪聲干擾能力。文獻［8］忽略高階模態對辨識結果的影響，通過模態參數特征靈敏度檢測出損傷位置和嚴重程度。

表1 工作模態參數辨識方法對比Tab.1 Work modal parameter identification methods contrast list

高壩等泄流結構具有高水頭、大流量和超高流速的特點，振動信號通常為低信噪比、非平穩隨機信號，其有效信息往往被低頻水流噪聲淹沒。為得到泄流結構振動特征，筆者提出一種適用于泄流結構的工作模態參數時域辨識方法。該方法通過對泄流振動數據進行預處理，提取結構振動有效信息，同時結合系統定階和模態驗證，為辨識高壩泄流結構的工作模態參數提供捷徑。

2 小波閾值-EMD濾波理論

對結構進行振動測試時，由于環境激勵響應、采集儀器的干擾和自身精確度偏差以及其他無法避免的人為因素，導致采集到的數據含有不同程度的噪聲，如果直接對實測振動信號進行模態參數辨識將嚴重影響辨識準確度。為此，選擇合適的降噪方法成為模態辨識研究的關鍵。

泄流結構振動信號是含高頻白噪聲和低頻水流噪聲的非平穩非線性信號。小波閾值降噪對白噪聲具有很強的抑制能力，通過閾值處理能濾除高頻白噪聲，其基本思想是在對含噪聲信號作小波分解后的各層系數中，對大于和小于某一閾值的小波系數分別進行處理，然后再利用處理后的小波系數重構原信號，以達到降噪目的。

對于泄流振動信號，由于結構振動真實信息常常被低頻水流噪聲淹沒，因此需要對小波閾值降噪后的信號進一步處理。EMD分解突破了傳統信號處理方法的瓶頸，不需要先驗知識選擇一些相應技術指標或者函數，從而降低人為誤差，其本質在于對信號進行強制平穩化處理，將信號中不同尺度的波動或趨勢逐級分解開來，產生一系列有限的具有不同特征尺度的本征模函數（intrinsicmodefunction，簡稱IMF）［9］。基于EMD的特點，可對小波閾值處理后的信號進行EMD分解。

筆者提出小波閾值與EMD聯合的降噪方法。該方法充分結合小波和EMD的優點，利用小波閾值分離信號中的高頻噪聲，抑制EMD端點效應，為EMD做鋪墊。EMD分解可進一步分離白噪聲和低頻水流噪聲，提高濾波降噪精度。其本質在于對有效信息表現出傳遞特性和對噪聲表現出抑制特性，根據有效信息和噪聲在小波分解尺度和EMD分解空間上的不同規律進行信噪分離。

小波閾值與EMD聯合降噪流程如圖1所示。其中，小波閾值的選取是處理過程的關鍵。由于硬閾值函數不連續，出現偽吉布斯現象，筆者采用軟閾值函數。Donoho［10］提出的閾值計算公式計算的是全局閾值，適用于高信噪比信號，對于被噪聲淹沒的低信噪比泄流振動信號，該閾值公式因保留太多較大的噪聲小波系數而影響降噪效果，且噪聲小波系數隨著分解層數的增加不斷降低。改進的閾值計算公式為

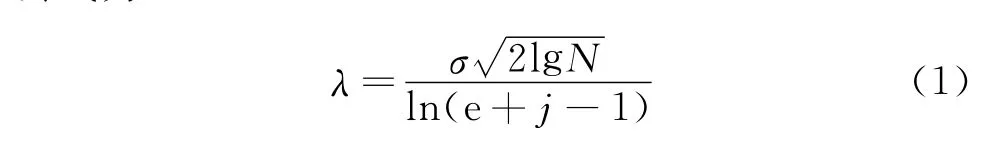
其中：σ為噪聲方差；N為信號數據長度；e表示底數e≈2.71828；j表示分解層數。

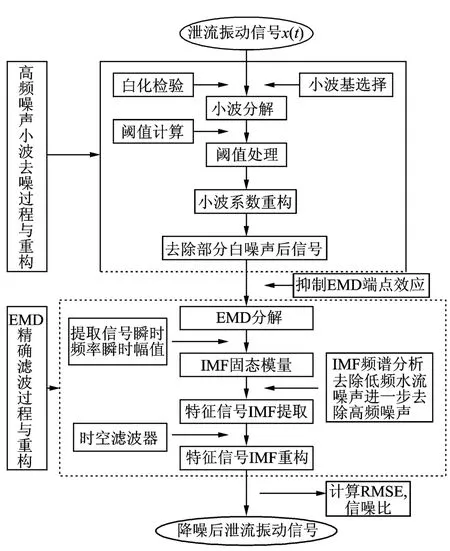
圖1 小波閾值-EMD聯合濾波方法流程Fig.1 Theflowchartofwaveletthreshold-EMDmethod

為評定信號降噪效果，引入信噪比（signalto noiseratio，簡稱SNR）和根均方誤差（rootmean squareerror，簡稱RMSE）作為評定標準。

信噪比為

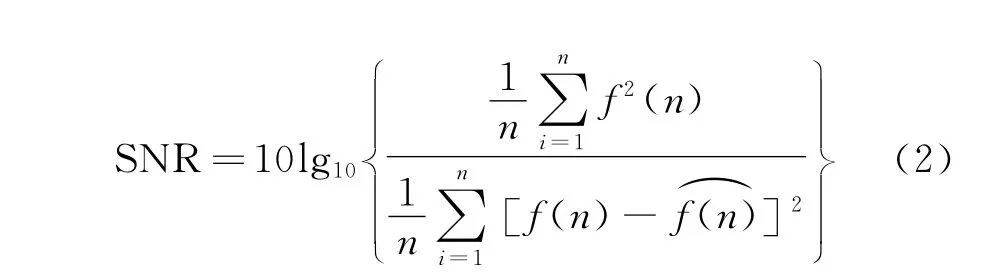
根均方誤差為

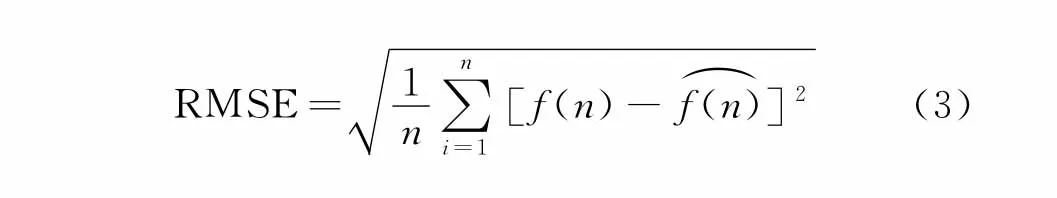
其中：f（n）和f（n）分別為原始信號和濾波后信號。

信噪比值越大，根均方誤差值越小，說明消噪效果越理想。

3 工作模態參數辨識理論

3.1 NEx T

NEx T是由美國Sandia國家實驗室結合時域模態分析方法而提出的［11］，線性系統在白噪聲激勵下兩點響應的互相關函數和脈沖響應函數的數學表達式完全一致。在互相關函數中，每個衰減的正弦函數都對應于某階結構模態，具有相同的固有頻率和阻尼比。因此，互相關函數可以用來代替脈沖響應函數進行模態參數辨識。

3.2 基于奇異熵增量的結構工作模態定階

脈沖響應數據構造的規范化Hankel矩陣反映的是脈沖響應信息矩陣，響應信號映射到m×n維相空間得到的重構吸引子軌道矩陣反映的是原始信號信息矩陣，兩者具有完全相同的構造形式［11］。引入奇異熵的概念對系統定階

其中：k為奇異熵的階次；ΔEi為奇異熵在階次i處的增量。

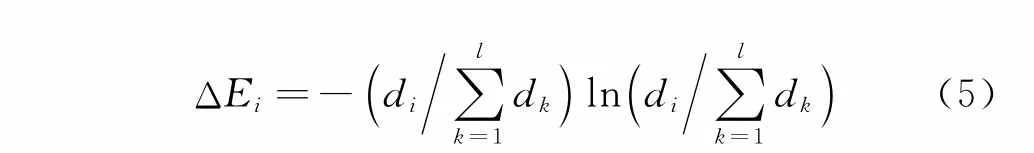
利用式（4）和式（5）計算規范化Hankel矩陣經奇異值分解后的奇異譜和奇異熵增量。同一脈沖響應信號無論受到噪聲干擾的程度如何，完整抽取其有效特征信息所需的奇異譜階次是一定的，即結構系統階次一定。因此，選取奇異熵增量開始降低到漸近值時的階次對結構系統進行模態定階。

3.3 HHT模態參數辨識

將脈沖響應函數進行EMD分解，得到結構的各階自由衰減響應，其函數表達式［12］為

其中：A0為與荷載強度、結構質量和頻率特性等有關的常數；ξ為相對阻尼系數；ω0為結構系統的無阻尼固有頻率；x0為初始位移；ωd為有阻尼固有頻率。

對各階自由衰減響應進行Hilbert變換（Hilbert transform，簡稱HT），得到（）x t的解析信號為

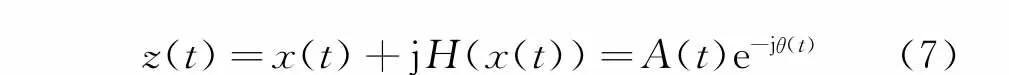
當系統中的阻尼較小時，式（7）中的幅值A（t）和相位θ（t）表示為

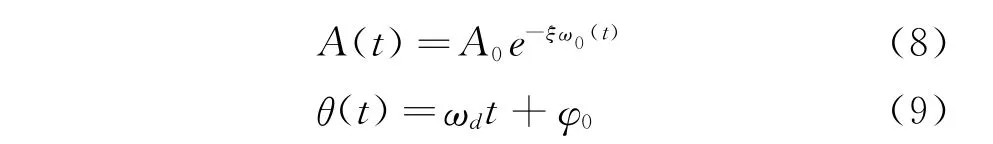
分別對幅值求自然對數，對相位函數求微分

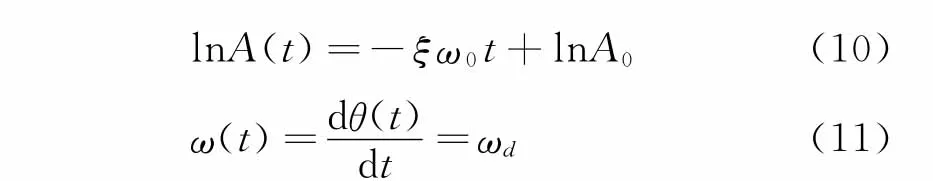
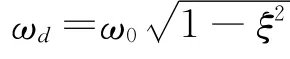
基于H HT的工作模態參數辨識步驟如下：

1）采用小波閾值-EMD聯合濾波方法對泄流結構振動信號（）x t進行濾波；

2）以振動量較小的測點為參考點并進行消噪處理，求同工況不同測點振動信號之間的互相關函數；

3）利用脈沖響應函數構造Hankel矩陣并進行奇異值分解；計算Hankel矩陣奇異值分解后的奇異熵，并確定奇異譜的階次（即結構系統階次），剔除非模態項（非共軛根）和共軛項（重復項），獲得結構實際階次；

4）對脈沖響應信號進行EMD分解得到的各階自由衰減響應分量進行Hilbert變換，求出幅值對數時間函數及相位時間函數，得到各階分量的固有頻率和阻尼比；

5）針對已確定的脈沖響應函數實際階次，結合模態置信度驗證模態，得到系統各階模態參數。

基于H HT的工作模態分析流程如圖2所示。

4 仿真分析

為檢驗小波閾值-EMD聯合濾波方法的濾波性能，構造模擬信號x（t）和x1（t）進行檢驗，其中x1（t）為加入低頻噪聲和高頻白噪聲的信號，表達式為

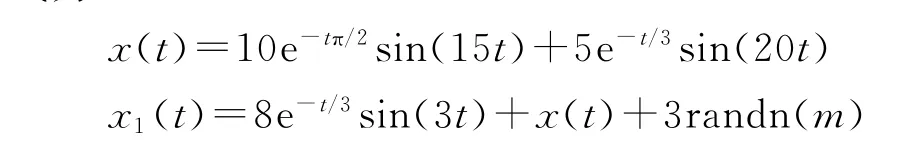
其中：t為時間；采樣頻率為100 Hz；采樣時間為10 s；randn（m）是均值為零、標準差為1的標準正態分布的白噪聲；m為樣本個數；假定振動幅值單位為μm。

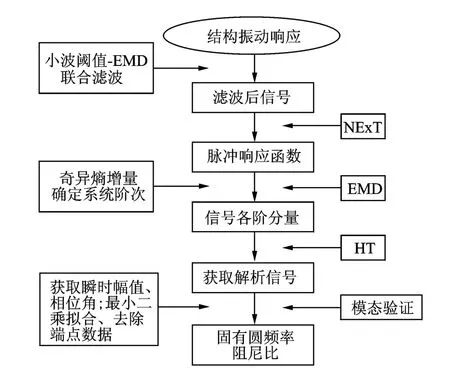
圖2 HHT工作模態分析流程圖Fig.2 The flowchart of HHT modal analysis

構造信號時程曲線如圖3所示。分別采用數字濾波、小波閾值濾波、EMD分解濾波和小波閾值-EMD聯合濾波方法對含噪信號x1（t）進行降噪分析。數字濾波選用IIR數字濾波器，技術指標根據原始信號頻譜選定。小波閾值降噪采用dB小波，根據白化檢驗自適應法確定分解層數為5層。EMD方法根據各階IMF頻譜圖判斷含真實信號的固態模量并對含真實信號的固態模量進行重構得到消噪后信號。4種濾波方法的消噪效果如表2所示。信號x1（t）消噪前后時程和功率譜密度圖如圖4，5所示。

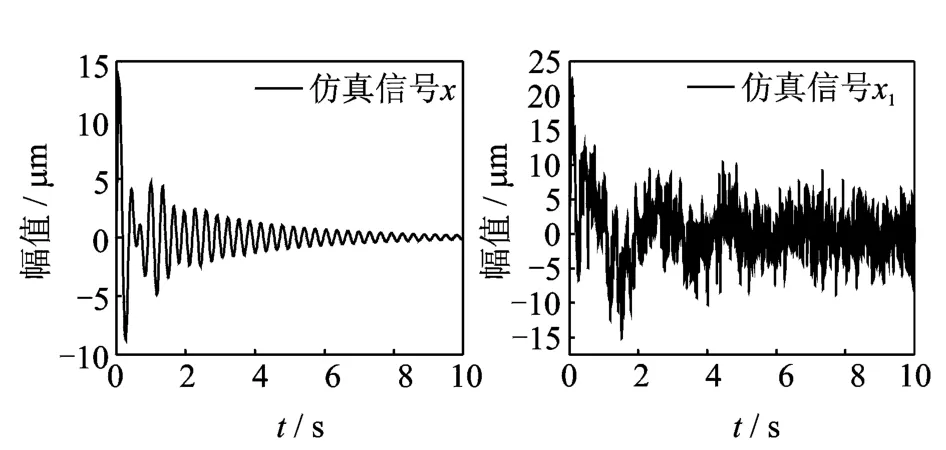
圖3 構造信號時程曲線Fig.3 Time history curves of signal

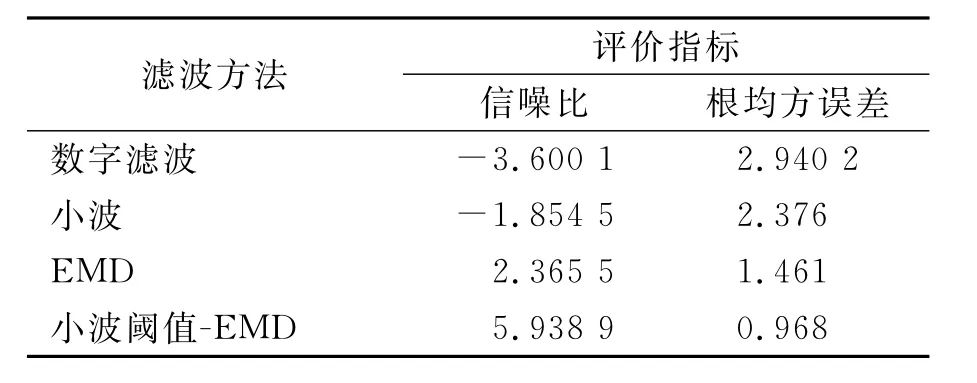
表2 信號x1采用4種濾波方法的消噪效果對比Tab.2 Denoising effect correlation table of signal x1by four method

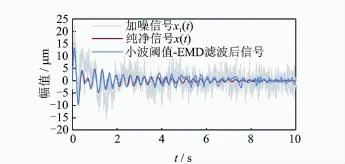
圖4 信號x1消噪前后對比圖Fig.4 The contrast diagram of raw signal and de-noised signal

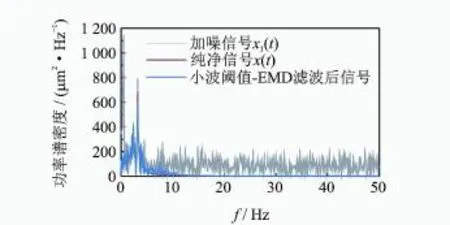
圖5 信號x1消噪前后功率譜密度對比圖Fig.5 The contrast diagram of power spectral density between raw signal and de-noised signal

由表2可知，采用小波閾值-EMD方法的降噪效果優于其他3種方法，該方法對于低信噪比信號濾波效果顯著，尤其適合于泄流結構振動信號。由圖5可知，當信號中噪聲能量很大時，有用特征信息往往被噪聲淹沒，尤其低頻脈沖噪聲已經淹沒了真實信號的優勢頻率，經過小波閾值-EMD聯合濾波，含噪信號中的噪聲成分已基本濾除，所保留信息能反映原始信號特征。

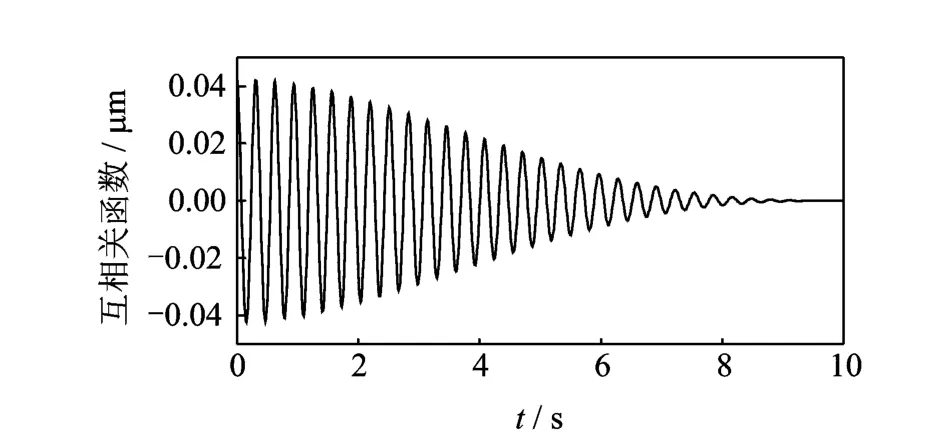
圖6 互相關函數曲線Fig.6 The curve of cross-correlation function

將濾波后信號做一時間延遲，得到二者之間的互相關函數，如圖6所示。將作為脈沖響應函數進行模態辨識，結合奇異熵增量隨奇異譜階次變化曲線對結構系統進行定階，奇異熵定階結果如圖7所示。當系統奇異譜階次為5階時，對應的奇異熵增量開始緩慢增長并逐漸趨于平穩。根據復模態理論，剔除系統非模態項（非共軛根）和共軛項（重復項）之后，系統的模態階次為2階。

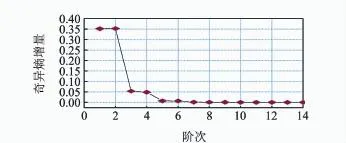
圖7 奇異熵增量隨奇異譜階次變化曲線Fig.7 The curve between increment of singular entropy and order

對脈沖響應函數進行EMD分解時，適時剔除序列兩端數據以抑制端點效應，保證所得包絡的失真度達到最小，提高分解質量。將各階分量進行Hilbert變換，求幅值對數曲線及相位函數曲線，對中間部分數據用最小二乘擬合得到固有頻率和阻尼比。各階分量模態辨識過程如圖8所示，辨識結果如表3所示。

由表3可知，仿真信號辨識誤差在5％以內，證明該方法的正確性及有效性。

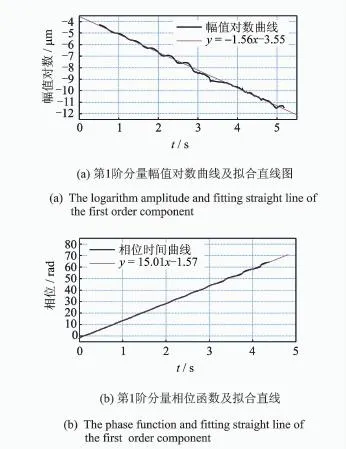
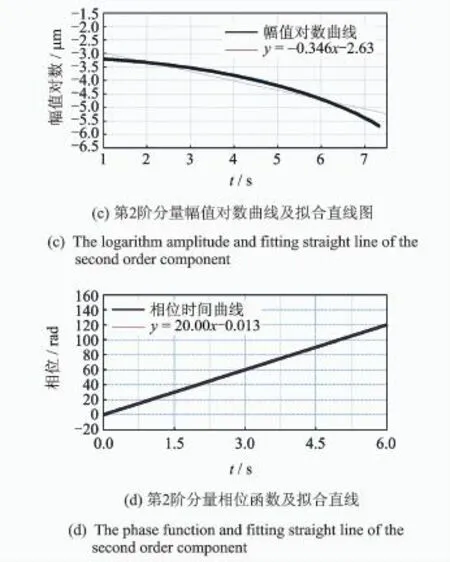
圖8 各階分量模態參數辨識過程Fig.8 Process of modal parameters identification

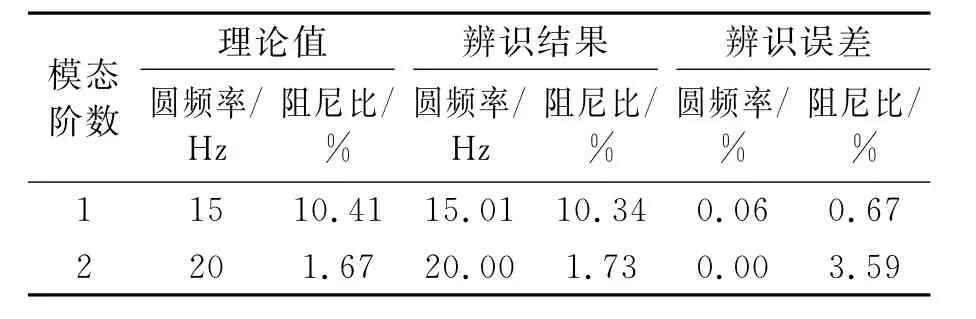
表3 模態參數識別結果Tab.3 The result of modal parameters identification

5 三峽重力壩工程實例

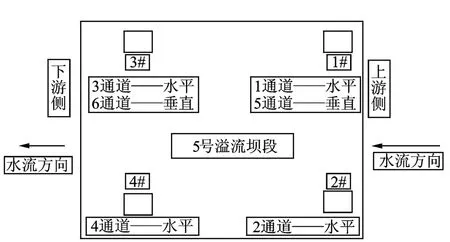
圖9 三峽5號壩段測點布置平面圖Fig.9 The measuring point layout chart of No.5 overflow section of three gorges gravity dam

為分析三峽重力壩泄流振動情況，選取5號溢流壩段為研究對象。壩頂上游側距離壩頂防浪墻3.6 m布置1#，2#測點，下游側距離壩頂走廊內側1.8 m布置3#，4#測點，測點布置平面圖如圖9所示。1#及3#測點布置水平向及垂向動位移傳感器，其他測點僅布置水平向動位移傳感器。1#，2#，3#，4#測點的水平向動位移傳感器試驗通道號分別為1，2，3，4；1#，3#測點的垂向動位移傳感器試驗通道號分別為5，6。

測試采樣頻率為100 Hz，采樣時間為40s，選擇1#和3#測點數據（即1，3，5，6通道）對該壩段進行工作模態參數辨識。限于篇幅，僅列第5階模態參數辨識過程（見圖10），模態參數辨識結果見表4。為說明H HT方法的實用性，與文獻［4］中的ERA方法辨識結果進行對比。ERA方法辨識精度高、能夠用于辨識密頻結構，并且與本研究方法辨識的模態參數具有相同的參數估計信息量和整體統一性。分析可知，筆者提出的HHT方法在辨識階數及辨識精度上優于ERA方法的辨識結果，且具有辨識密頻模態的能力。

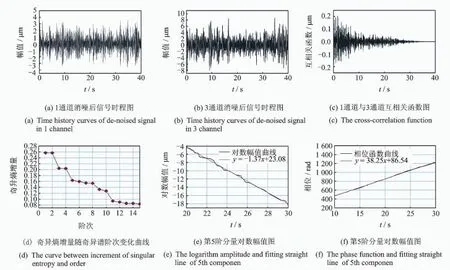
圖10 第5階模態參數辨識過程圖Fig.10 Process of modal parameters identification of 5th component

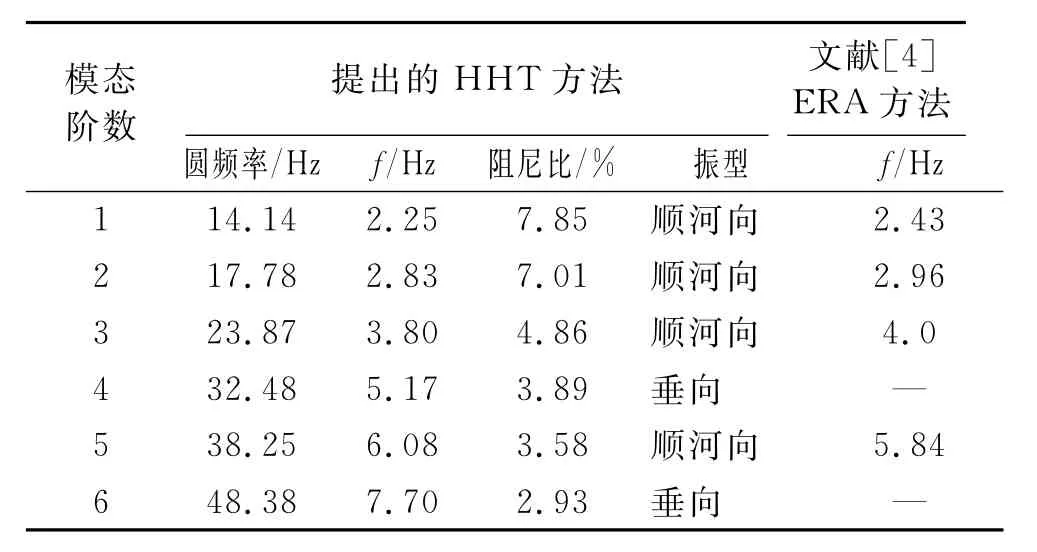
表4 三峽5號溢流壩段模態參數辨識結果Tab.4 The result of modal parameters identification of No.5 overflow section of three gorges gravity dam

6 結 論

1）小波閾值-EMD聯合濾波方法是一種適用于泄流結構振動分析的信號降噪方法，較傳統濾波方法具有更佳的降噪效果。

2）結合奇異熵增量系統模態定階，H HT工作模態參數辨識方法能夠直接確定系統階數并準確辨識出泄流結構模態參數，能夠有效避免模態分解中的頻率混雜，具有較強的魯棒性以及較高的辨識精度。

3）該方法為模態參數的整體辨識方法，具有辨識密頻模態的能力，為辨識高壩泄流結構的工作模態參數提供捷徑。

［1］ 史東鋒，許鋒，申凡，等.結構在環境激勵下的模態參數辨識［J］.航空學報，2004，25（2）：125-129.Shi Dongfeng，Xu Feng，Shen Fan，et al.Modal parameter identification of structure in ambient excitation ［J］.Acta Aeronautica Et Astronautica Sinica，2004，25（2）：125-129.（in Chinese）

［2］ 張建偉，李火坤，練繼建，等.基于環境激勵的廠房結構損傷診斷與安全評價［J］.振動、測試與診斷，2012，32（4）：670-674.Zhang Jianwei，Li Huokun，Lian Jijian，et al.Damage diagnosis and safety evaluation of underground powerhouse under ambient excitation［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（4）：670-674.（in Chinese）

［3］ 張建偉，張翌娜，趙瑜.泄流激勵下水工結構應變模態參數時域辨識研究［J］.水力發電學報，2012，31（3）：199-203.Zhang Jianwei，Zhang Yina，Zhao Yu.Study on strain modal parameters identification of hydraulic structure in time domain under discharge excitations［J］.Journal of Hydroelectric Engineering，2012，31（3）：199-203.（in Chinese）

［4］ 張建偉.基于泄流激勵的水工結構動力學反問題研究［D］.天津：天津大學，2008.

［5］ 章國穩，湯寶平，孟利波.基于特征值分解的隨機子空間算法研究［J］.振動與沖擊，2012，31（7）：74-78.Zhang Guowen，Tang Baoping，Meng Libo.Improved stochastic subspace identification algorithm based on eigendecomposition［J］.Journal of Vibration and Shock，2012，31（7）：74-78.（in Chinese）

［6］ Chang M W，Pakzad S N.Modified natural excitation technique for stochastic modal identification［J］.Journal of Structural Engineering，2013，139（10）：1753-1762.

［7］ Sarparast H，Ashory M R，Hajiazizi M.Estimation of modal parameters for structurally damped systems using wavelet transform［J］.European Journal of Mechanics A-solids，2014，47：82-91.

［8］ Yan Wangji，Ren Weixin.Closed-form modal flexibility sensitivity and its application to structural damage detection without modal truncation error［J］.Journal of Vibration and Control，2014，20（12）：1816-1830.

［9］ Xu Lisheng，Shen Yanhua，Zhong Yue，et al.EMD-based adaptive wavelet threshold for pulse wave denoising［J］.International Federation for Medical and Brological Engineering Proceedings，2013，39：367-370.

［10］Donoho D L.Denoisng by soft-thresholding［J］.IEEE Transaction on Information，1995，3：613-627.

［11］練繼建，李火坤，張建偉.基于奇異熵定階降噪的水工結構振動模態ERA識別方法［J］.中國科學，2008，38（9）：1398-1413.Lian Jijian，Li Huokun，Zhang Jianwei.The ERA identification method in hydraulic structure vibration modal based on singular entropy order selection and denoising ［J］.Science in China Press，2008，38（9）：1398-1413.（in Chinese）

［12］李成業.泄流結構水力拍振機理及動態健康監測技術研究［D］.天津：天津大學，2013.

10.16450/j.cnki.issn.1004-6801.2015.04.029

TV31；TV32+3；TH825

張建偉，男，1979年3月生，博士、副教授。主要研究方向為水工結構耦聯振動與安全。曾發表《水工結構泄流激勵動力學反問題研究進展》（《水利學報》2009年第40卷第11期）等論文。

E-mail：zjwcivil@126.com

*國家自然科學基金資助項目（51009066）；河南省高等學校青年骨干教師資助計劃（2012GGJS-101）；河南省科技攻關

（142102310122，142300410177，132102310320）；華北水利水電大學研究生教育創新計劃基金資助項目（YK2014-05）

2014-11-10；

2015-03-10