拓撲優化技術在橋梁截面優化設計中的應用研究

常 誠

（山西省交通科學研究院，山西 太原 030006）

0 引言

近年來，我國的公路建設高速發展，興建了大量的橋梁工程，在設計過程中，橋梁各構件的截面（如主梁截面、橋墩截面、斜拉橋的塔柱截面等）優化設計尤為重要，基于此，本文提出了拓撲優化技術在截面優化中的應用。

根據研究對象的不同，拓撲優化可以分為離散拓撲優化與連續體拓撲優化。1964年，Dron等人提出了基結構法，將數值方法引入結構設計領域，該方法將實際結構離散為桿件連接而成的基結構，通過優化算法將多余的桿件從結構中剔除，從而獲取最優構形。Rozvany等人建立了桁架結構拓撲優化的最優準則，根據這一準則，可以在完備的設計域中確定最優解。

謝憶民和Steven于1992年提出了漸進結構優化算法（ESO），此方法可以解決靜態、動態結構的尺寸、形狀和拓撲優化問題。該方法基本概念簡單，而且具有較好的通用性，可借助當前通用的有限元分析軟件作為分析平臺。榮見華等人[1-2]提出了基于靈敏度的漸進結構優化算法和基于人工材料的拓撲優化設計方法。劉毅[5]提出了基于固定網格的雙向漸進結構優化方法，將雙向固定網格漸進結構優化方法應用于符合材料板殼開孔形狀優化。

漸進結構優化算法的另一特點是雙向進化[3]。傳統的漸進結構優化算法主要依靠刪除單元來獲取優化構形。但是由于在某些迭代過程中，一些單元會被過度刪除，之后無法恢復，因此其準確性受到影響，從而限制了此方法的應用。基于應力準則的雙向優化算法，其原理是在高應力單元周圍增加單元，在低應力區刪除低應力單元，使得單元殺死和單元生成同時進行，提高了算法的適應性。

1 拓撲優化算法

本文實現的拓撲優化技術基于漸進結構優化算法（ESO）。其基本原理為：不斷地從連續體中剔除傳力效率不高的單元，最后生成結構的主要荷載傳遞構架。優化的目標是：以最少的材料、最合理的拓撲形狀，來實現結構總體剛度的最大化，即結構應變能密度的最小化[4]。優化的目標函數為：

式中：Ci為結構中第i個單元的應變能；Wi為第i個單元的重量。

定義結構的性能指標[5]為：

C0、W0、Ci、Wi分別表示初始狀態下及經過第 i次優化后結構的總應變能和總重量。

對平面應力狀態下的各向同性材料，可采用Mises應力準則[6]：

式中：σVM是單元的 Mises應力；σ1、σ2、σ3分別代表第一主應力、第二主應力與第三主應力。

首先求出每點的應力值，假設第j個單元的單元應力為σj，結構中某此迭代的最大單元應力為，則如果

則認為該單元應力偏小，利用單元殺死技術將該單元剛度設置為一個極小值，其中RRj為單元刪除率。

通過迭代求解，當式（4）無法滿足時，即已達到穩定狀態。為使有效迭代繼續進行，引入一個進化參數ER，進化公式為：

2 算例

2.1 算例1

某混凝土簡支梁，長70 cm，高30 cm，底部承受如圖1所示的集中力，F=50 kN。材料彈性模量E=3.25×1010Pa，密度 ρ=2 300 kg/m3，泊松比 λ=0.3。有限單元類型為Plane42，單元尺寸esize=0.5 cm，共劃分5 600個四邊形單元。

圖1 簡支梁示意圖（單位：mm）

圖2 第22次迭代

圖3 第45次迭代

圖4 第109次迭代

圖2～圖4分別為結構在第22、45、109次的迭代求解結果，其中圖4為最優拓撲構形。從圖中可以看出，迭代初期，單元的刪除從遠離荷載一側的兩個端角點開始，并在結構中部兩集中荷載之間形成矩形孔洞。迭代進行到第45步時，兩集中力上方分別優化出3根“桿”，矩形孔洞進一步增大；在第109次迭代時，3根桿件進化為2根，拱結構進一步細化，結構優化指標PI達到最大值。

2.2 算例2

某混凝土懸臂梁，長50 cm，高20 cm，端部承受如圖5所示的集中力，F=30 kN。材料彈性模量E=3.25×1010Pa，密度 ρ=2 300 kg/m3，泊松比 λ=0.3。有限單元類型為Plane42，單元尺寸esize=0.5 cm，共劃分4 000個四邊形單元。

圖5 懸臂梁示意圖（單位：mm）

圖6 第80次迭代

圖7 第128次迭代

圖8 第168次迭代

圖6～圖8分別為結構在第80、128、168次的迭代求解結果，其中圖8為最優拓撲構形。從圖中可以看出最優構形為“半拱形”結構。其中“拱腹桿”位置與拉、壓應力跡線的走向類似。

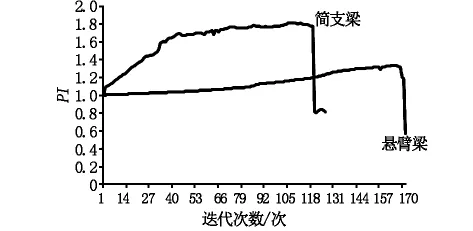
圖9 結構優化指標PI

根據式(2)可知，指標PI越大，說明拓撲構形越合理，材料利用率越高。簡支梁與懸臂梁算例的PI的變化趨勢如圖9所示。從圖中可以看出兩者的指標分別在第109次迭代與第168次迭代中達到最大，這與兩算例分別在第109次迭代與第168次迭代中獲取最優構形是相符的。

3 結論

基于漸進結構優化算法的思想，本文實現了連續體結構的拓撲優化技術。該技術主要依靠低效率單元的刪除策略來獲取最優拓撲構形。該技術依托通用有限元軟件ANSYS，通過編制APDL程序來實現。數值算例表明，該算法具有較好的計算穩定性。本文算法同樣適用于三維問題以及同時考慮應力和位移約束的問題，對橋梁各構件的截面優化設計具有實際工程意義。