超寬預應力混凝土箱梁的空間效應研究

羅昊沖，宋力勛

（天津市市政工程設計研究院，天津市 300457）

0 引言

隨著社會經濟的快速發展，城市化進程不斷加快，城市快速路系統發展日益成熟，目前多個城市均發展各自的快速路系統。而隨著城市的快速發展，交通量也日益提高，超寬箱梁橋則成為城市高架橋設計的首選；同時，由于凈空的限制、景觀的要求，城市高架橋普遍設計為大懸臂。此類超寬箱梁的特點有：寬跨比大、寬高比大、梁高低、翼板寬。由于上述構造特點，超寬箱梁在縱向受力方面與傳統箱梁有明顯差異，表現為明顯的空間效應。一方面，寬箱梁的各條腹板受力較為不均衡；另一方面，寬箱梁表現出較為明顯的剪力滯效應。

對于梁橋的縱向受力分析，傳統的方法是采用平面桿系的單梁法計算，該方法以平截面假定為基礎，只能得出箱梁截面同一高度的平均應力水平。該方法計算方便快捷，精度可以滿足絕大部分寬跨比較小的直線橋梁。但是對于大懸臂超寬箱梁，采用平面單梁模型進行分析可能會產生較大偏差。為了研究空間效應對超寬箱梁縱向受力的影響，本文以長春市快速路工程中的一聯變幅超寬連續箱梁為背景，采用空間實體有限元模型進行計算分析。

1 工程概況與計算模型

工程算例為某工程（33+35+33）m現澆預應力連續箱梁，橋寬從40.5 m到29.7 m變化，梁高2.0 m，斷面形式為單箱七室，流線型大懸臂設計。預應力體系采用縱向預應力加橋面板橫向預應力。混凝土強度等級為C50，采用整體支架現澆法施工，橫斷面見圖1。

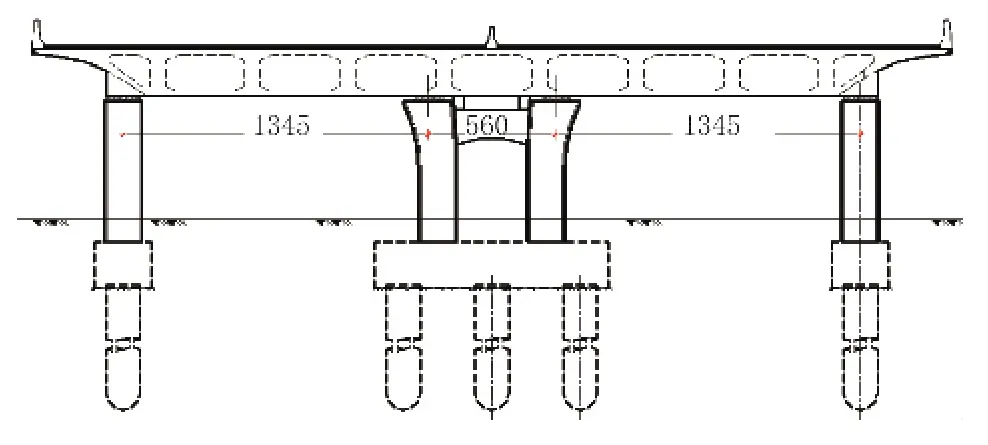
圖1 箱梁橫斷面圖（單位：cm）

本文采用空間有限元程序MIDAS FEA建立全橋實體模型計算分析。由于結構橫橋向對稱，模型只取橫橋向一半結構，對稱中心面采用相應約束，計算模型見圖2。計算考慮了自重、二期恒載、預應力、梯度溫度等荷載工況。

圖2 全橋實體有限元模型

2 超寬箱梁各腹板受力差異的分析

對于超寬橋梁，腹板數較多，各腹板之間的受力差異也較大。本文針對實體分析的應力結果，在各腹板范圍內進行積分求得了各腹板所承受的彎矩和剪力值。考慮的縱向截面位置見圖3，橫截面的腹板編號見圖4，自重及二期作用和縱向預應力作用下各腹板的彎矩值和剪力值見圖5。

圖3 順橋向截面位置示意圖

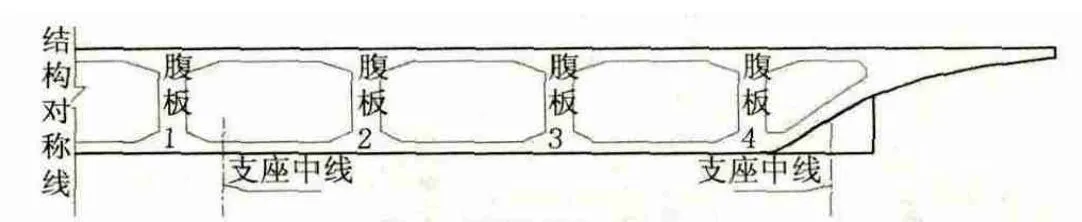
圖4 腹板編號示意圖

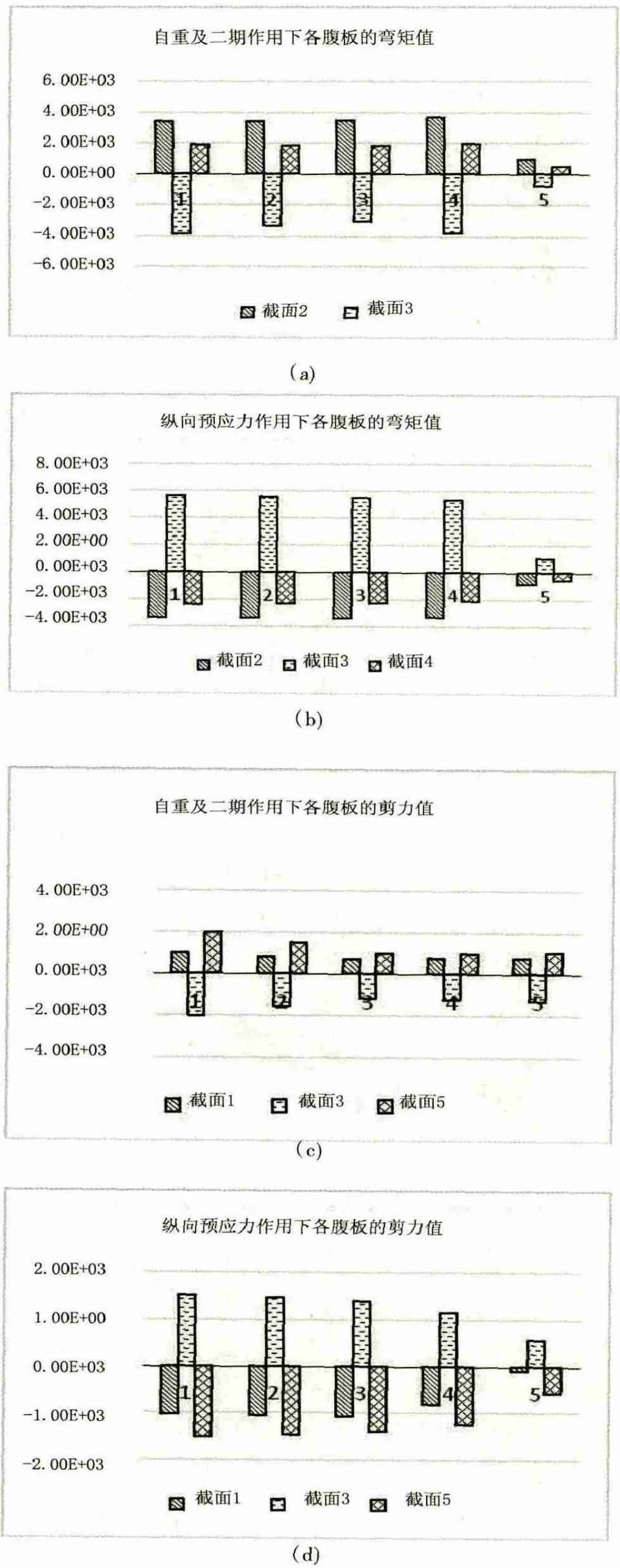
圖5 荷載作用下各腹板的內力值

自重及二期作用和縱向預應力作用下，各腹板彎矩剪力值與全截面平均值之間的最大偏差百分比見表1。由于截面1和截面7的彎矩值很小，截面2、4、6的剪力值很小，這些情況的偏差計算沒有實際意義，因而表中未予列出。

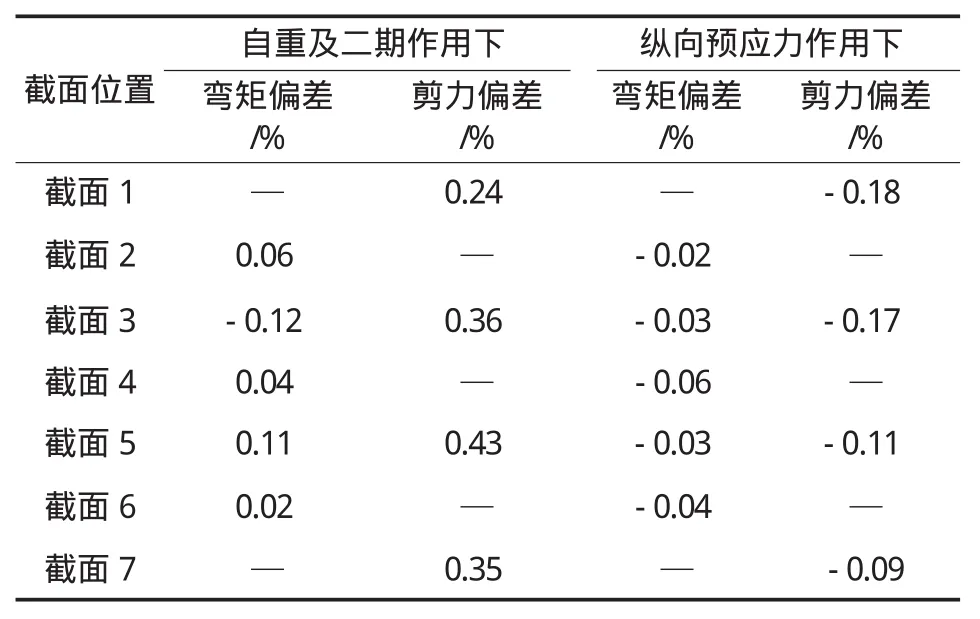
表1 各腹板內力的偏差值

由圖5和表1中數據可以看出：跨中截面的內力偏差不明顯，但支點截面的內力偏差較大，靠近支座的腹板彎矩值大于其他腹板，這是由于橫梁具有一定柔性而造成的。各腹板的剪力差異較大，偏差百分比甚至超過40%，而彎矩偏差不超過12%。自重及二期作用下各腹板的內力差異大于縱向預應力作用下的差異。另外，外緣斜腹板承受的彎矩較小，但承受的剪力較大。

3 超寬箱梁的剪力滯效應分析

由于剪力滯的影響，在荷載作用下，箱梁縱向正應力延截面橫向分布是不均勻的，截面1至截面4在各種荷載作用下的頂緣正應力分布見圖6。

為了方便地描述剪力滯效應的影響程度，引入剪力滯系數的概念，其值等于截面上實際發生的應力與用初等梁理論算出的應力之比值。依據實體模型的應力結果，可以求得各截面不同橫向位置的剪力滯系數，其中各種荷載作用下每個截面頂板最大剪力滯系數見表2。

由圖6和表2中數據可知：自重及二期荷載作用下的剪力滯效應較為復雜，沒有表現出明顯的規律性；縱向預應力作用下的支點截面表現出明顯且規律的正剪力滯效應，即腹板附近的應力大于其他位置，且在懸臂處應力值明顯減小；在恒載組合（即自重+二期+縱向預應力）工況下，支點截面表現出明顯的正剪力滯效應，跨中截面剪力滯效應不明顯且不規律。另外，正梯度溫度作用下各截面表現出明顯的負剪力滯效應。

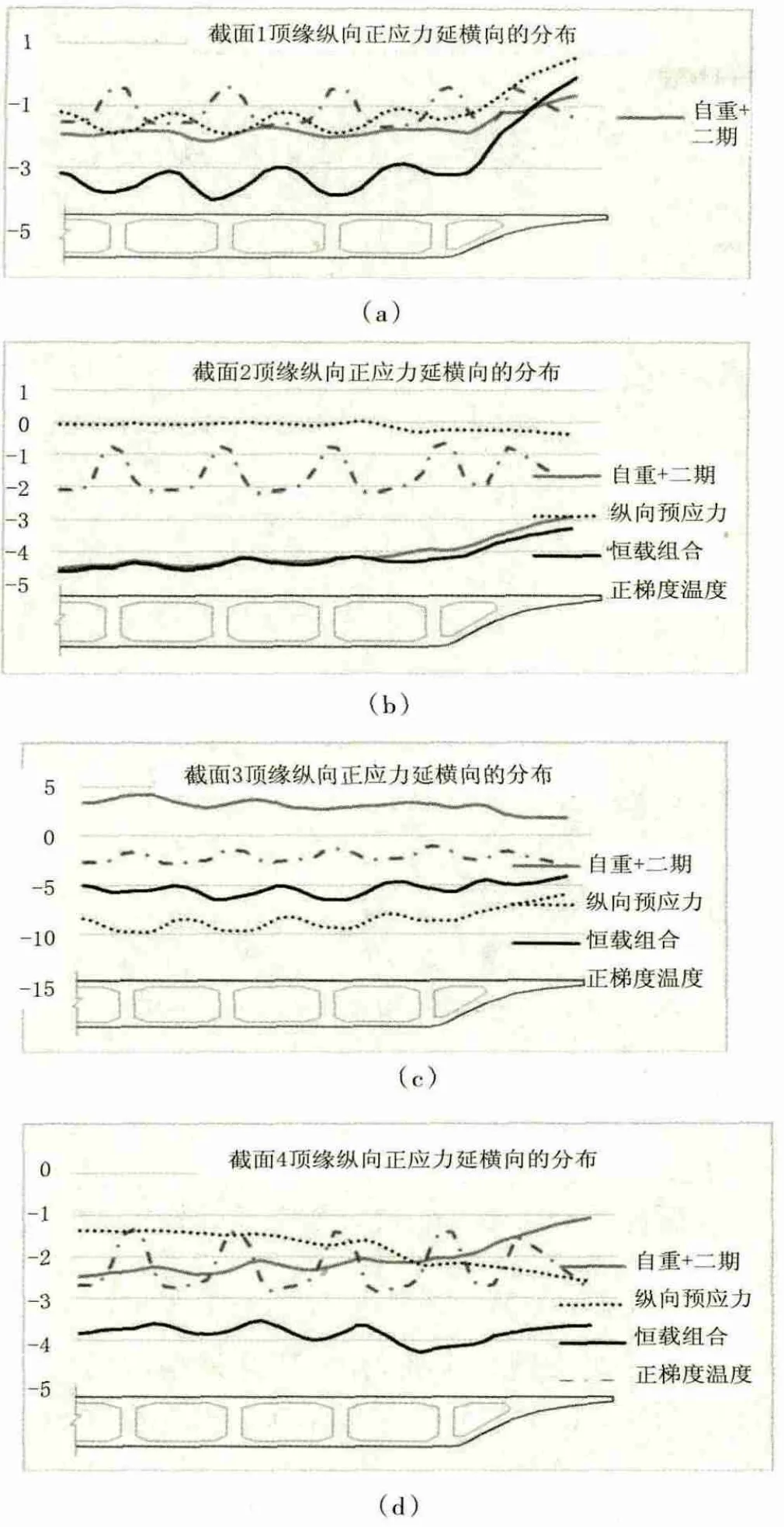
圖6 各截面頂緣縱向正應力延橫向的分布

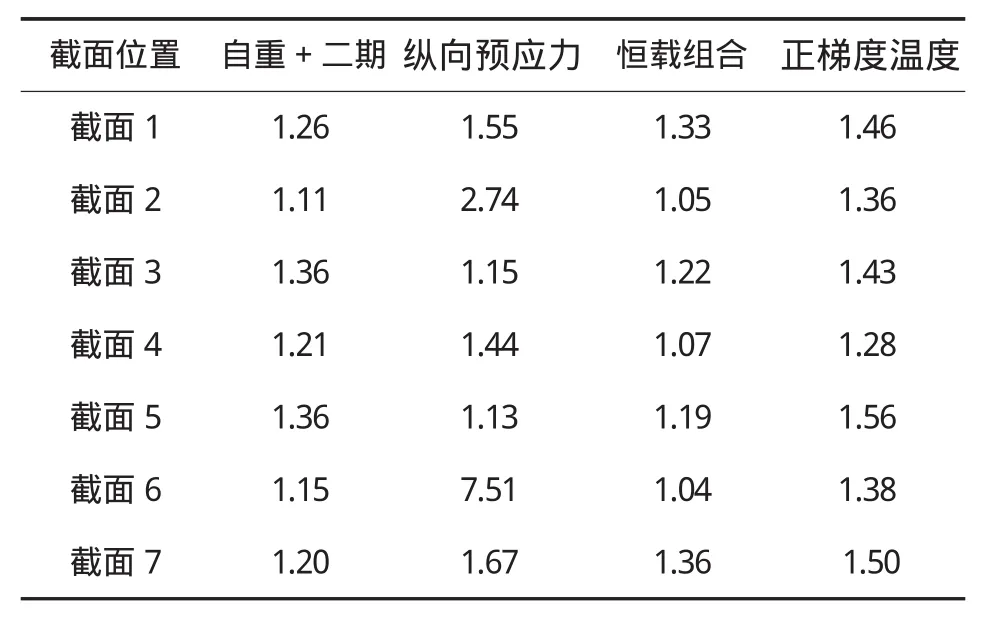
表2 各截面的最大剪力滯系數

關于剪力滯系數的大小有如下結論：支點截面的剪力滯系數一般大于跨中截面。恒載組合下支點截面的剪力滯系數在1.19～1.36之間；跨中截面則較小，不超過1.07。梯度溫度作用下的剪力滯系數較大，在1.28～1.56之間。

4 結論

（1）對于超寬箱梁，跨中截面各腹板的受力差異不明顯，但支點附近差異則較大。支點處彎矩偏差接近12%，而剪力偏差甚至超過40%。

（2）在恒載組合工況下，支點截面表現出明顯的正剪力滯效應，剪力滯系數在1.19～1.36之間；而跨中截面的剪力滯效應較弱，不超過1.07。

（3）用平面單梁模型進行分析設計時，支點附近的配筋和應力控制須預留適當的富余度，尤其是抗剪設計需要足夠保守。

[1]彭德運,丁敬,李正.城市高架橋連續寬箱梁空間效應研究[J].公路,2012(8):142-146.

[2]蘭昌榮,楊允表.大懸臂扁平多室箱梁結構的空間分析[J].上海公路,2010(2):40-43.

[3]曲慧明.寬箱梁剪力滯效應分析[D].重慶:重慶交通學院,2003.