預(yù)應(yīng)力混凝土梁管道注漿質(zhì)量的頻率檢測法研究

竇雁輝，冉志紅，伍玉寶，卓郅穎

(云南大學(xué)城市建設(shè)與管理學(xué)院，云南昆明 650091)

預(yù)應(yīng)力混凝土梁管道注漿質(zhì)量的頻率檢測法研究

竇雁輝，冉志紅，伍玉寶，卓郅穎

(云南大學(xué)城市建設(shè)與管理學(xué)院，云南昆明 650091)

基于Ansys模擬計算，分別對預(yù)應(yīng)力混凝土梁在鋼絞線注漿和沒注漿兩種情況下，當(dāng)鋼絞線受到張拉力時對整個梁體的頻率影響進(jìn)行分析研究，發(fā)現(xiàn)預(yù)應(yīng)力混凝土梁在鋼絞線注漿之后一階頻率比無注漿狀態(tài)下有50%左右的變化量，之后隨著張拉力的增大，梁體的各階頻率仍成上升趨勢，但是改變量非常小。驗證了Clough的受軸力作用的梁體頻率變化理論，提出了基于梁體頻率變化的注漿與否的無損檢測方法。

橋梁工程；預(yù)應(yīng)力混凝土梁；鋼絞線；頻率檢測法；管道注漿

0 引言

在我國的橋梁建設(shè)中，裝配式預(yù)應(yīng)力混凝土梁橋，憑借其結(jié)構(gòu)簡單、造價低、施工方便的特點在中國的橋梁建設(shè)中占有非常重要的地位，且數(shù)量極其龐大。在這類橋梁的承載力評定中，其上部結(jié)構(gòu)中預(yù)制梁體的質(zhì)量是最重要的部分，而在預(yù)應(yīng)力梁中，為了充分發(fā)揮混凝土抗壓強(qiáng)度遠(yuǎn)大于抗拉強(qiáng)度的特點，目前均采用張拉鋼絞線的方法來克服大跨度情況下混凝土自重引起的下緣拉應(yīng)力。在張拉鋼絞線之后，注漿密實度是評判預(yù)應(yīng)力鋼絞線和混凝土能否協(xié)同工作的重要指標(biāo)，但是目前注漿密實度的檢測尚沒有非常可靠的方法，本文從動力分析的角度對注漿質(zhì)量的檢測進(jìn)行了研究。

1 預(yù)應(yīng)力混凝土梁的自振頻率研究現(xiàn)狀

近年來，預(yù)應(yīng)力和混凝土預(yù)制梁頻率關(guān)系的研究一直是許多學(xué)者感興趣的話題。根據(jù)Clough R W,Penzien J的理論，體系在軸向力作用下有效剛度減小［1］，因此振動頻率亦下降，但是將預(yù)應(yīng)力看作混凝土的軸向受壓是不合適的，因為預(yù)應(yīng)力混凝土是鋼絞線和混凝土一起工作的兩種材料，不能單純看作兩端的軸力。1994年Saiidi M［2］等人制作了一根計算長度3 660 mm，截面尺寸b× h=102 mm×127 mm的矩形試驗梁，記錄了不同大小預(yù)應(yīng)力狀態(tài)下梁的自振頻率，測試結(jié)果表明其頻率隨預(yù)應(yīng)力的增加而增加。2008年，華中科技大學(xué)李瑞鴿［3］博士在前人研究的基礎(chǔ)上，制作了一根b×h=120 mm×240 mm，計算長度3 700 mm的矩形梁，采用無粘結(jié)預(yù)應(yīng)力，其試驗結(jié)果依然是頻率隨著預(yù)應(yīng)力的增加而增加，但是她認(rèn)為前人將預(yù)應(yīng)力混凝土看作各向同性材料是不合適的，于是她將預(yù)應(yīng)力混凝土視為正交異性材料進(jìn)行了計算，但是正交異性材料的物理性能參數(shù)大多是經(jīng)驗數(shù)值，所以難免也有誤差。

2 Ansys模擬計算

本文采用的分析對象是實際工程中某連續(xù)梁橋的一片30 m的T梁，設(shè)計強(qiáng)度C50，三束鋼絞線均采用9φs15.2低松弛fpk=1 860 MPa抗拉強(qiáng)度的鋼絞線，具體參數(shù)見表1。

表1 30 m T梁材料特性參數(shù)

T梁尺寸參數(shù)和鋼絞線位置坐標(biāo)采用的是2008版交通部上部結(jié)構(gòu)30mT梁通用圖。由于實際T梁是變截面的，而且是鋼絞線和混凝土共同工作，簡化成結(jié)構(gòu)動力學(xué)中有限自由度的方法去計算非常麻煩，而且無法考慮空間效應(yīng)，所以采用大型通用有限元分析軟件Ansys進(jìn)行模擬計算。

本計算模型主要研究鋼絞線與混凝土的關(guān)系，在模擬分析時采用solid65作為鋼筋混凝土實體單元。該單元是經(jīng)過非線性處理的，可以模擬混凝土的開裂、壓碎、塑性變形和徐變。鋼絞線采用link10單元(見圖1)，它是一個軸向僅受拉或近受壓三維單元，當(dāng)使用受拉選項時，單元剛度會在受壓時消失，其初應(yīng)變由給出△/L0，△為單元長度L與零應(yīng)變L0的差值，負(fù)值表示其處于松弛狀態(tài)，所以在考慮預(yù)應(yīng)力時，需要給鋼絞線一個正值的初應(yīng)變。鋼絞線和混凝土耦合方向如圖2，模型耦合情況如圖3。

圖1 link10單元特性

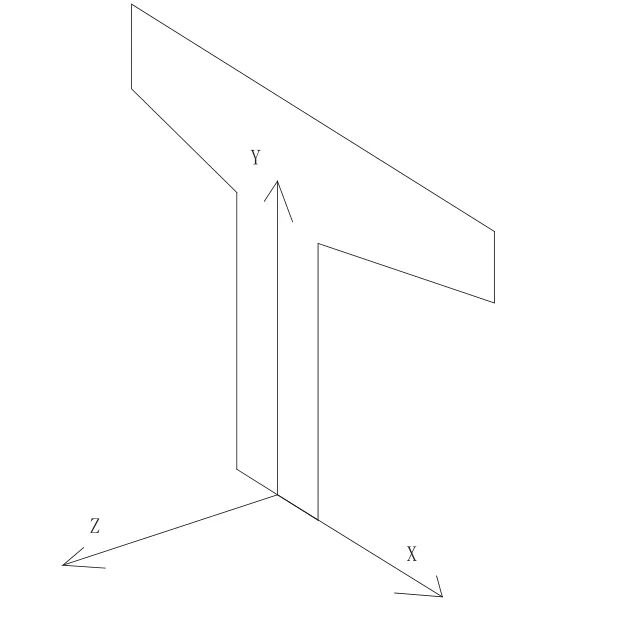
圖2 鋼絞線和混凝土耦合方向

圖3 Ansys耦合模型

自由度在Ansys中耦合時，需要在劃分完單元后將鋼絞線的所有單元節(jié)點定義為一個集合，然后采用nnear(nod)函數(shù)自動搜尋距離鋼絞線最近的混凝土節(jié)點來耦合。注漿與否主要體現(xiàn)在鋼絞線與混凝土之間是否有粘結(jié)力上，單束耦合數(shù)據(jù)如表2。

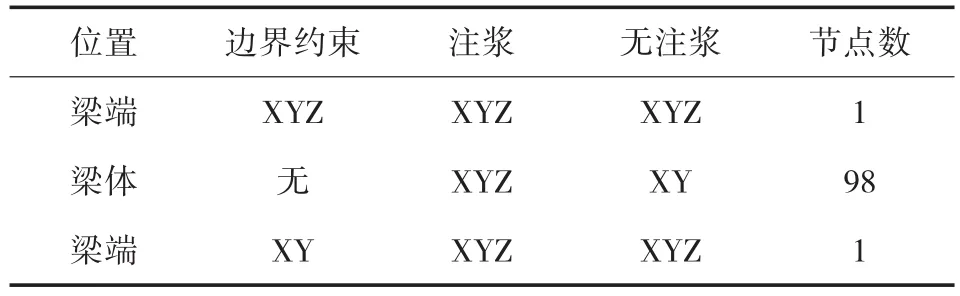
表2 邊界條件及單束鋼絞線耦合情況

鋼絞線的張拉控制強(qiáng)度為0.75 fpk=1 395 MPa，采用給鋼絞線初應(yīng)變的方法分級加載模擬計算預(yù)應(yīng)力作用下混凝土的模態(tài)，計算時候需要在打開［pstres,on］進(jìn)行靜力分析之后，再次打開［pstres,on］來進(jìn)行預(yù)加力作用下的模態(tài)分析。有粘結(jié)和無粘結(jié)的預(yù)應(yīng)力混凝土頻率變化情況見表3。

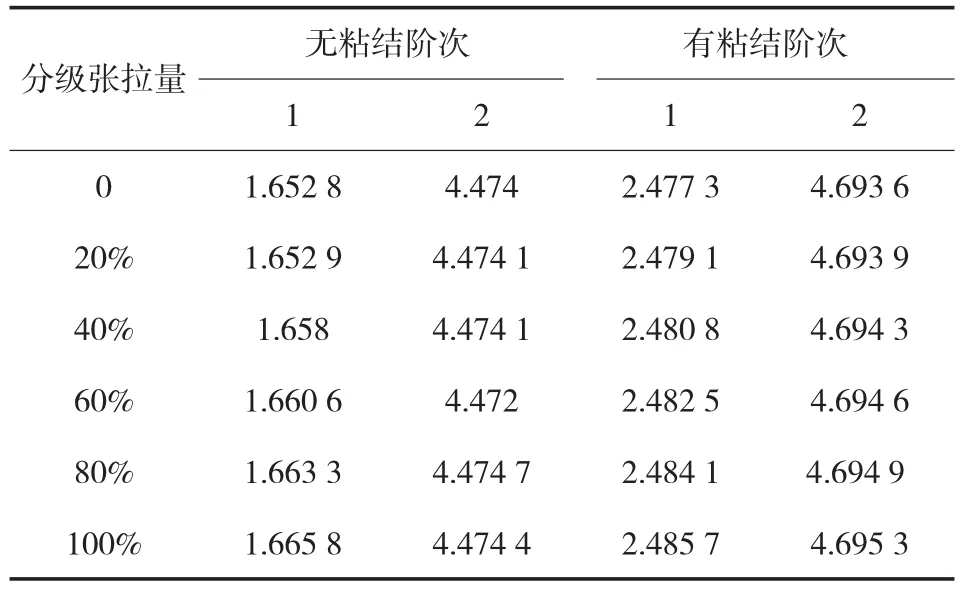
表3 無粘結(jié)和有粘結(jié)前兩階頻率

通過表3的計算結(jié)果可以看出，在預(yù)應(yīng)力作用下，梁的頻率并沒有明顯的提高，無粘結(jié)和有粘結(jié)的預(yù)應(yīng)力從0到100%其一階頻率增長量分別為0.78%和0.34%，但是一階頻率從無粘結(jié)到有粘結(jié)變化量幾乎達(dá)到了50%，但是隨著階數(shù)的升高其變化量逐漸降低如圖4。

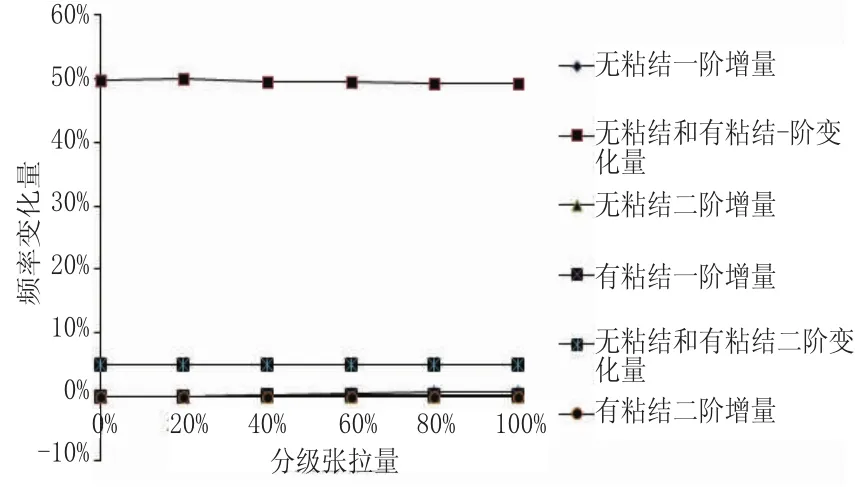
圖4 有粘結(jié)和無粘結(jié)頻率變化量

所以，通過測試一階頻率的變化來檢測是否注漿從理論上來講是可行的。由于鋼絞線的彈性模量大于混凝土，而且鋼絞線抗拉能力非常強(qiáng)，所以在注漿之后鋼絞線和混凝土粘結(jié)在一起，使梁體的剛度增加。但是，無注漿的鋼絞線與混凝土分離，只是在張拉的情況下微小的提高剛度。

3 Clough理論驗證

為了進(jìn)一步說明預(yù)應(yīng)力對混凝土影響的問題，依據(jù)Clough的理論，受軸力作用下的梁的自由振動微分方程如下：

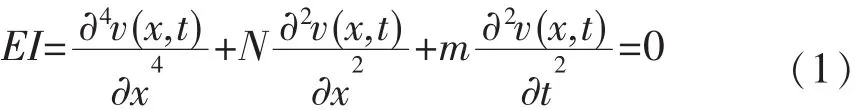
通過邊界條件解得自振圓頻率為：

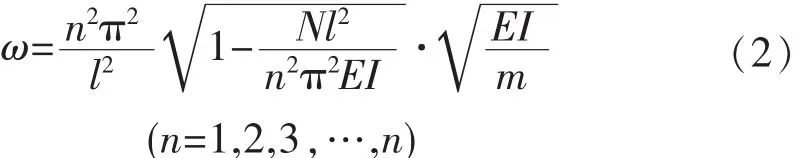
顯然在軸力N的作用下，頻率隨著軸力的增加而降低。為此擬在模型中約束為XY的一端施加等同于100%張拉的一集中壓力F=(1.757e+6N)進(jìn)行模擬驗證，加載示意圖見圖5。

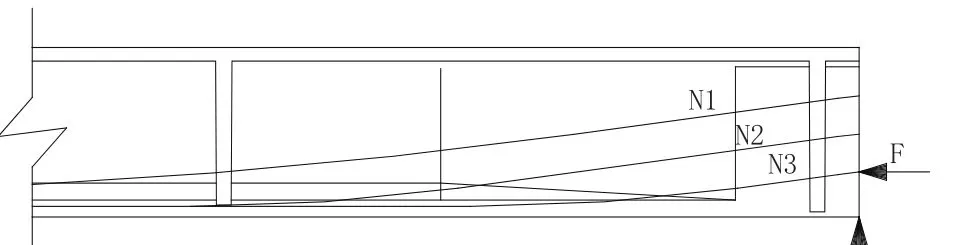
圖5 軸力F加載示意圖

經(jīng)過模擬計算前五階頻率，無粘結(jié)和有粘結(jié)軸力作用下的頻率相對于100%張拉時頻率下降量的百分比的情況如圖6。

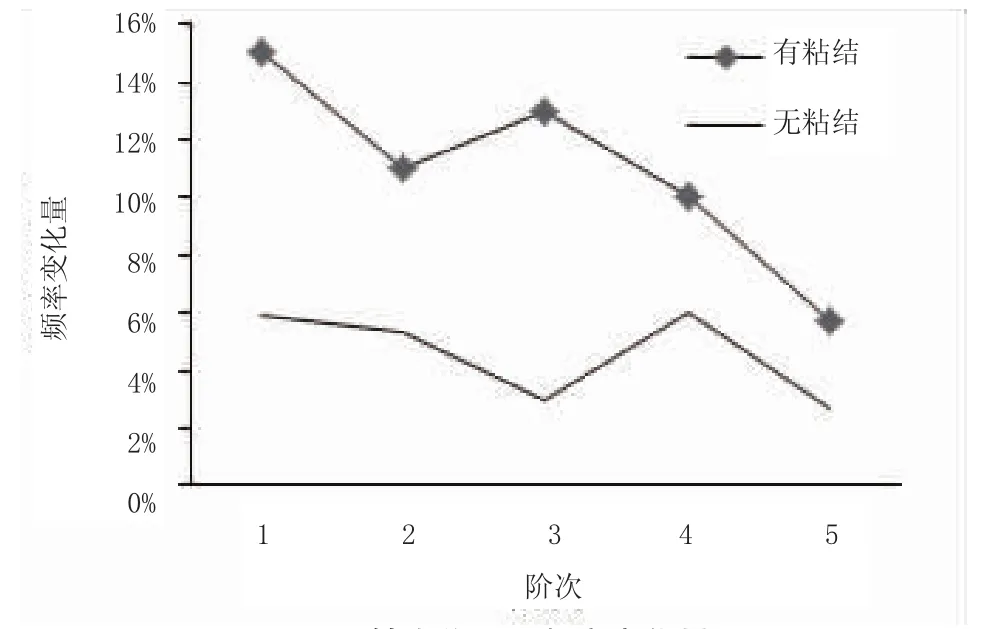
圖6 軸力作用下頻率變化量

從圖6可以看出有粘結(jié)和無粘結(jié)梁的前五階頻率在軸力作用下都有下降。在Clough版結(jié)構(gòu)動力學(xué)里，受軸力影響的構(gòu)件頻率分析中，假設(shè)條件是軸力影響頻率的討論都是認(rèn)為軸向力的作用線平行于構(gòu)件未變形的原始軸線，并假定在結(jié)構(gòu)發(fā)生運(yùn)動時它的作用線方向和大小不變。實際情況下，鋼絞線是曲線，而且鋼絞線和混凝土注漿耦合在一起后，應(yīng)從材料的角度去分析，所以將預(yù)應(yīng)力梁簡單地看作兩端軸向受壓來分析就忽略了鋼絞線和混凝土的耦合工作效果，這樣是不合適的。

4 注漿前后頻率計算方法

做預(yù)應(yīng)力混凝土梁的頻率分析計算時，由于鋼絞線和混凝土在注漿后是一個整體，而且預(yù)應(yīng)力的影響非常小，可以暫時忽略預(yù)應(yīng)力大小對頻率的影響效果，從材料的角度去分析，將梁的振動微分方程中去掉軸力項，其頻率應(yīng)該按式(3)計算：

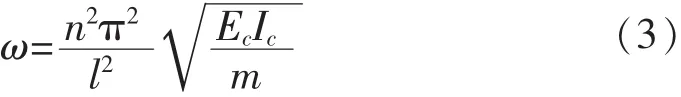
EcIc是鋼絞線和混凝土注漿之后耦合在一起的剛度，但是其混合剛度的EcIc計算目前仍沒有很好的計算理論和方法。

注漿前后頻率的變化量如式(4)：

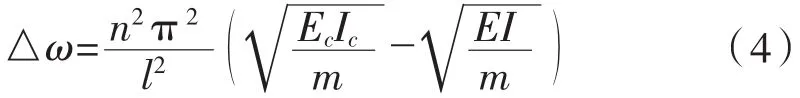
EI為無注漿時預(yù)應(yīng)力混凝土梁的剛度，無注漿時，鋼絞線對混凝土梁幾乎沒有剛度的提高(非常微弱)。

5 結(jié)論和展望

模擬計算的結(jié)果表明：預(yù)應(yīng)力可以使梁的自振頻率升高，但是變化量非常不明顯，幾乎可以忽略，所以計算預(yù)應(yīng)力梁的自振頻率時可以忽略其影響。但是從材料的角度來看，有粘結(jié)和無粘結(jié)的預(yù)應(yīng)力混凝土梁存在明顯的剛度差異，實際狀態(tài)也就等同于波紋管內(nèi)是否注漿，注漿之后鋼絞線和混凝土可以看作一個整體，其剛度增加，所以通過值的獲取來判別預(yù)應(yīng)力梁是否注漿從理論上來講是可行的。但是，預(yù)應(yīng)力混凝土動力性能的研究還有許多工作要做。

(1)由于實際制梁場中的梁的邊界條件與計算模型不符，所以本文對是否注漿的檢測仍停留在理論階段，還需要大量的試驗數(shù)據(jù)來驗證其實際可行性。

(2)注漿狀態(tài)的鋼絞線，其拉應(yīng)力延鋼絞線方向引起的混凝土受壓情況對梁體頻率的影響尚不清楚。

(3)由于混凝土受壓不受拉，鋼絞線受拉不受壓，所以其注漿后的混合剛度的確定仍沒有可靠的計算理論和方法。

(4)無粘結(jié)預(yù)應(yīng)力混凝土梁在振動時鋼絞線和混凝土相互影響的情況還需要大量的研究。

［1］ Clough R W, PenzienJ.Dynamic of structures ［M］.USA∶McGraw Hill,1982.

［2］ Saiidi M, Douglas B, Feng S. Prestress force effect on vibration frequency of concrete bridges［J］.Journal of Structural Engineering, 1994,120(7)∶2233-2241.

［3］ 李瑞鴿 張耀庭. 基于正交異性材料的預(yù)應(yīng)力梁頻率的試驗研究［J］.工程力學(xué), 2008, 25(2)∶116-120.

［4］ 周寧. ANSYS-APDL高級工程應(yīng)用實例分析與二次開發(fā)［M］.北京：中國水利水電出版社,2007.

［5］ 曹樹謙,張文德.振動結(jié)構(gòu)模態(tài)分析-理論、試驗與應(yīng)用［M］.天津大學(xué)出版社,2001.

［6］ 馬樂為,徐趙東.結(jié)構(gòu)動力學(xué)［M］.北京：科學(xué)出版社,2007.

U443.35

A

1009-7716(2015)08-0216-03

2015-03-18

國家自然科學(xué)基金(51208452)

竇雁輝(1987-)，男，河南鄭州人，碩士研究生在讀，研究方向為橋梁損傷檢測、施工監(jiān)控和長期監(jiān)測。