基于MIGA的動力總成懸置系統優化設計

賀新峰 陳國棟 卜繼玲 丁行武

基于MIGA的動力總成懸置系統優化設計

賀新峰 陳國棟 卜繼玲 丁行武

（株洲時代新材料科技股份有限公司）

針對某款動力總成懸置系統隔振性能較差的問題，對該懸置系統進行了分析與優化。建立了懸置系統的動力學仿真模型，通過系統模態和解耦率評價隔振性能。采用多島遺傳算法，以解耦率、系統模態為優化目標和約束進行集成優化設計。優化后，主要激振方向的解耦率由86.4%提高到91.46%，主要激振方向模態的最小間隔為4.13 Hz。在顯著提高懸置系統隔振性能的同時可滿足動力總成布置空間需求。

1 前言

目前的研究工作主要是通過懸置布置來達到解耦目的，或通過優化算法對懸置的各向剛度參數進行優化達到解耦與頻率分布合理的目的。通過懸置布置達到解耦的方法通常應用于有較大布置空間的情況；通過優化算法達到解耦目的的方法應用范圍較廣，可以對頻率分布和振動解耦率進行優化。文獻[1]深入分析了傳統懸置V形布置理論并擴展了其設計方法，為動力總成懸置系統的彈性解耦設計提供了完善的理論依據；文獻[2]以廣義力傳遞率積分和極小化為目標，以動力總成懸置系統的剛體振動模態頻率分布范圍為約束，實現了懸置系統布置參數和懸置元件剛度的優化；文獻[3]以懸置系統解耦為目標，以懸置各向剛度為設計變量，采用遺傳算法對動力總成懸置系統進行了優化設計。

本文集成MSC.Adams與Isight，采用多島遺傳算法對某動力總成懸置系統進行了優化設計。在MSC.Ad?ams中建立了動力總成懸置系統的動力學模型，并計算了該動力總成的剛體模態和解耦率。將解耦率作為優化目標，以懸置系統位置參數和剛度參數為變量，以頻率分布為約束，進行了優化設計。最后在整車運行工況下，對動力總成的位移和轉角進行了驗證。

2 動力總成懸置系統固有頻率和解耦特性分析

動力總成懸置系統固有頻率分布是否合適，是評價動力總成懸置系統性能的一個重要指標。有激勵方向的振動固有頻率與其它頻率的間隔不能太小，以防激起寬頻振動，為隔振帶來困難。根據隔振原理，只有激勵頻率與固有頻率的比值大于時，懸置系統才可以起到隔振作用，因此發動機正常運行時的最小頻率與動力總成懸置系統最大固有頻率的比值應大于。

為了避免一個方向的激勵激起多個方向的劇烈振動，需要關注動力總成懸置系統各個方向的解耦情況。能量解耦法是從能量角度實現各自由度的解耦。在動力總成曲軸坐標系中，懸置系統在作各階主振動時，其能量全部集中在6個方向。根據動力總成的質量矩陣及振型矩陣，可求出動力總成在作各階主振動時的能量分布，得到某階模態下的解耦程度。

3 多島遺傳算法

多島遺傳算法建立在傳統遺傳算法基礎上[4]，其不同于傳統遺傳算法的特點是每個種群的個體被分成幾個子群，這些子群稱為“島”。傳統遺傳算法的所有操作分別在每個島上進行，每個島上選定的個體定期遷移到其它島上，然后繼續進行傳統遺傳算法操作。多島遺傳算法中的遷徙操作保持了優化解的多樣性，提高了包含全局最優解的機會。

多島遺傳算法在優化過程中，首先利用初始值進行優化操作，初步達到收斂后，由于變異和遷徙的作用，在一個新的初值點開始重新進行遺傳操作，如此重復操作，可以避免局部最優解，從而抑制了早熟現象的發生。

基于多島遺傳算法的動力總成懸置系統優化設計流程如圖1所示。

4 應用實例

4.1 動力總成懸置系統動力學模型的建立

本文以某重型汽車的動力總成懸置系統為研究對象，該系統質量為1 474 kg，質心坐標為（-303.44 mm，-5.95 mm，121.18mm），動力總成轉動慣量和慣性積在動力總成質心坐標系下測試得到。各懸置初始位置和懸置傾角如表1所示，懸置傾角是指懸置z向坐標軸與動力總成垂直方向的夾角。懸置初始剛度值如表2所示。根據表1和表2中的初始數據以及動力總成的質量參數和質心坐標在MSC.Adams中建立懸置系統的動力學模型如圖2所示。動力總成質心坐標和懸置位置坐標在懸置系統坐標系中測試得到，懸置系統坐標系是以發動機飛輪后端蓋面與曲軸中心線的交點為坐標原點，以自由端向飛輪端的指向為x軸正向，垂直向上為z向，通過右手法則確定y向，如圖3所示。

表1 動力總成懸置位置參數

表2 動力總成懸置剛度參數 N/mm

4.2 優化設計

該動力總成為6缸發動機，缸體為V型布置，其慣性力和慣性力矩完全平衡[5]，所以該發動機的唯一激振是由點火引起的扭轉振動。該扭轉振動是繞x軸的周期振動，為了防止繞x軸的激勵引起動力總成其它方向的振動，要求繞x軸轉動方向的模態解耦率較高。此外，動力總成懸置系統要求頻率合理分布。在初始數值條件下懸置系統的解耦率與頻率如表3所示。

表3 動力總成懸置系統解耦率與頻率

優化時，以懸置位置、傾角以及各向剛度參數為設計變量，位置傾角參數變量范圍如表1所示，剛度參數變量范圍如表2所示。與激振力同向的關鍵模態頻率與其它模態頻率的最小間距大于1 Hz；系統最大頻率小于16 Hz；有激振力方向的解耦率大于90%，其它方向解耦率大于85%為約束；各向解耦率之和最大為優化目標；采用多島遺傳算法進行優化設計。

動力總成懸置系統優化設計的數學模型表示為：

式中，Xj為懸置位置變量；Sj為懸置剛度變量；XjL、XjH為位置變量上、下限；SjL、SjH為剛度變量上、下限；Ei為沿各向的最大振動能量百分比，其中E4為繞x軸方向的最大振動能量百分比；fi為懸置系統各階頻率，其中f4為繞x軸的轉動頻率；fmax為最大模態頻率。

從表3可以看出，優化后繞x軸振動方向的解耦率由優化前的86.4%提高到91.46%，其它各向解耦率也得到很大提升；繞x軸振動的固有頻率與其它頻率的最小間隔為4.13 Hz，避免了繞x軸的激勵引起其它方向的振動。其它各向的最小頻率間隔由原來的0.09 Hz提高到0.71 Hz。

采用優化前、后的位置和剛度參數分別建立動力學模型，計算車輛在各種運行工況下動力總成質心的最大位移和轉角如表4所示。可知，優化后各向的位移和轉角有不同程度的減小，節約了動力總成布置空間，可有效避免與周圍其它部件發生干涉。

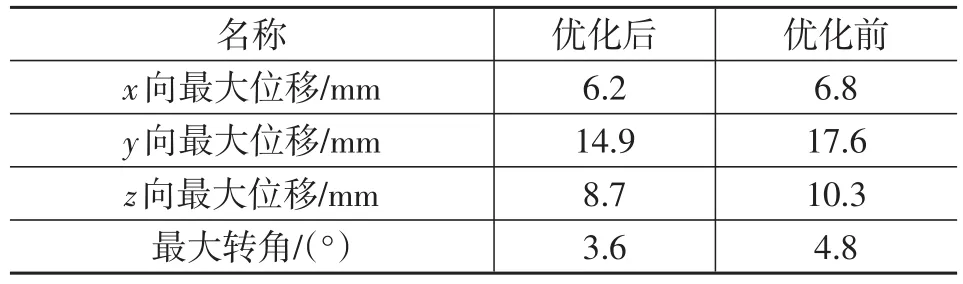
表4 動力總成懸置系統質心位移和轉角

5 結束語

a.由于同時將動力總成各懸置的位置和剛度參數作為設計變量，懸置系統更容易達到合理的隔振效果；

b.采用多島遺傳算法進行優化設計，有效避免了由于設計變量較多而產生的局部最優解；

c.優化后，提高了動力總成懸置系統的解耦率，改善了懸置系統隔振性能，具有較高的工程實用價值。

1 呂振華，范讓林.動力總成—懸置系統振動解耦設計方法.機械工程學報，2005，41（4）:49～54.

2 王亞楠，呂振華.以廣義力傳遞率為目標的動力總成隔振懸置系統優化設計方法.機械工程學報，2011，47（11）: 52～58.

3 付江華，史文庫等.基于遺傳算法的汽車動力總成懸置系統優化研究.振動與沖擊，2010，29（10）:187～190.

4 Hong B，Soh T Y，Pey L P.Development of a helicopter blade FE model using MIGA optimization.AIAAJournal，2004，4:1～8.

5 何渝生，魏克嚴，洪宗林，孫祥根編著.汽車振動學.北京：人民交通出版社.1990.

6 Chen B.single-and multi-abjective optimization of scramjet components using genetic algorithms based on a parabolized navier-stokes solver.AIAA Journal，2006，7:1～18.

7 Jeong T，Singh R.Analytical methods of decoupling the auto?motive engine torque roll axis.Journal of sound and vibra?tion，200，234（1）:85～114.

8 戶原春彥.防振橡膠及應用.北京：中國鐵道出版社，1982.

（責任編輯簾 青）

修改稿收到日期為2015年3月1日。

Optimization Design of Powertrain Mount System based on MIGA

He Xinfeng,Chen Guodong,Bu Jiling,Ding Xingwu
（Zhuzhou Times New Materials Technology Co.,Ltd）

For a powertrain mount system with poor vibration isolation performance,analysis and optimization are made.The dynamics simulation model of mount system is built,and the performance of vibration isolation is evaluated by system modal and decoupling rate.The integrated optimization is made by using the multi-Island genetic algorithm, with decoupling rate and system modal as optimization objective and restraint.The results show that after optimization, decoupling rate of main excitation direction increases from 86.4%to 91.46%,and the minimum interval of modal frequency of main excitation direction is 4.13Hz.Vibration isolation performance of the mount system is improved significantly,and the layout space requirements of the powertrain are also met.

Powertrain mount system,Optimization,Decoupling rate,MIGA

動力總成懸置系統 優化 解耦率 多島遺傳算法

U463.33

A

1000-3703（2015）05-0035-03