基于因子分析的高校學生分層培養

任澤民，袁玉興

(重慶科技學院數理學院，重慶 401331)

一、背景

中國的高等教育發生了許多變化，已由精英教育轉變為大眾教育，大學校園也轉變為培養“人”的搖籃。大學生初進大學校園會面對角色的轉變、學習內容和方式的轉變、彼此間價值觀的碰撞等諸多問題。因此，關注學生不同方面的需求，積極地引導學生進入健康的學習環境中很有必要［1］。對學生，尤其對考研學生的成績需更為全面地了解，以便學校實施更為有效的分層培養模式［2］。

為了給考研學生和學校管理者提供有效的參考依據，本文利用因子分析方法對某屆應用數學專業的學生進行分析，從眾多的影響考研成績的學習科目中合理選擇4種綜合因素進行分析。由此，學生可以有意識、針對性地提高此四方面的素質。學校可以根據這些因素制定相應的培養策略。

二、因子分析模型與基本步驟

假定p個變量X1，X2，…，Xn，且每個變量具有 E(Xi)=0和D(Xi)=1。因子分析模型是將原始的變量k個變量(f1，f2，…，fk)線性表達，即有

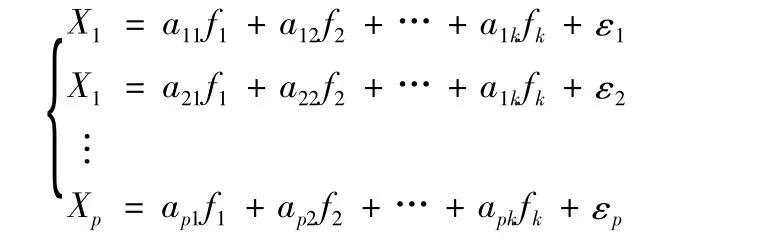
上式可寫成矩陣表達形式為X=AF+ε，其中F為公因子。實踐者可以通過如下的步驟進行因子分析:

(1)檢驗滿足因子分析的條件:進行原始變量相關度分析，若存在顯著線性關系則可以提取因子;

(2)提取公因子:利用主成分方法，在盡可能減少變量個數的同時保證信息的完整性;

(3)因子重命名:處理因子的載荷矩陣，使得原始變量可被清楚的解釋;

(4)計算因子得分:生成成分得分系數矩陣，列出公因子的得分函數。

三、基于因子分析模型的學生成績分析

本文的研究對象來自重慶某高校應用數學專業學生的成績。

1.原始變量選擇

根據回歸分析［3］，第一類學生的專業基礎課與考驗成績存在明顯的正相關關系。在進行變量指標選擇時需將該類學生的專業基礎課和公共基礎課所包含的課程成績選定為分析變量。其中專業基礎課包括:高等代數1－2、數學分析1－3、解析幾何、常微分方程、復變函數、概率論與數理統計、實變函數;公共基礎課包括:大學英語1－4、英語口語1－2、思想道德與修養、馬克思哲學、中國近代史、毛鄧三1－2。

2.相關度分析

對上述選擇的變量通過SPSS軟件［4－6］進行相關性分析獲取相關系數矩陣，部分結果見表1。

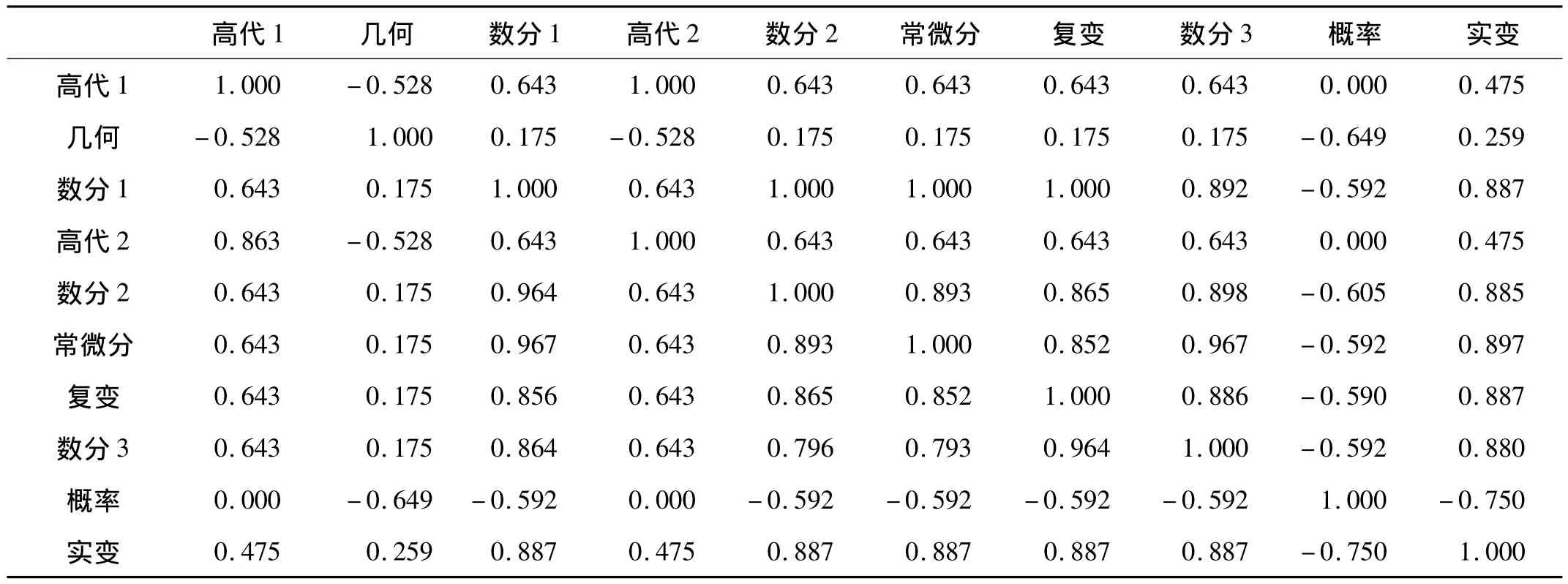
表1 相關矩陣

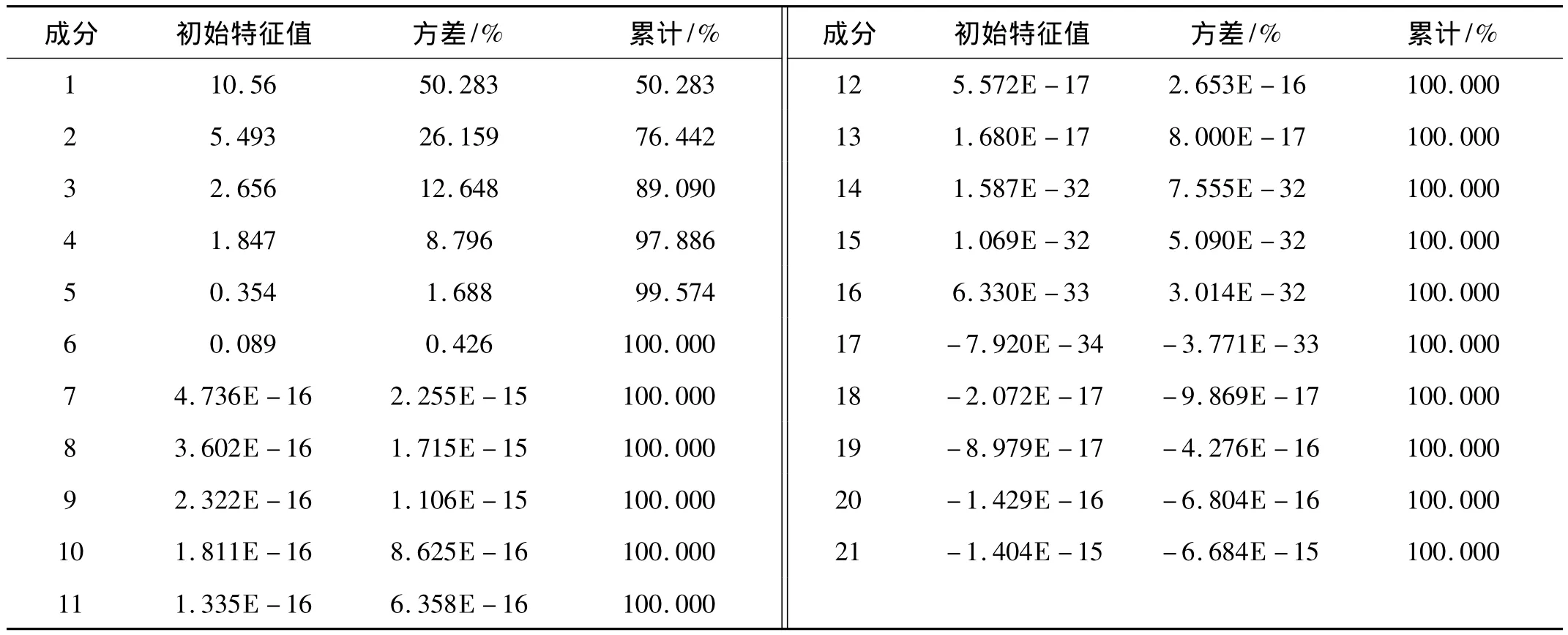
表2 因子解釋原始變量情況

從表1可以看出，大部分變量存在較高的相關系數，且具有較強的線性關系。因而可以提出公因子，對原變量進行因子分析。

3.進行因子分析

第一步:根據原始變量的相關性，利用主成分分析方法提取公因子。從表2中數據看出，前4個因子共同解釋了原始變量總方差的97.886%，故提取前4個因子不會丟失很多信息且明顯減少變量個數想。從因子碎石圖(見圖1)中可以更加直觀地看到:第1個因子貢獻最大，更充分解釋原始變量;第2、第3、第4個因子都可以解釋一部分變量;第5個因子之后的貢獻都很小，可以被忽略。所以提取前4個因子是合適的。

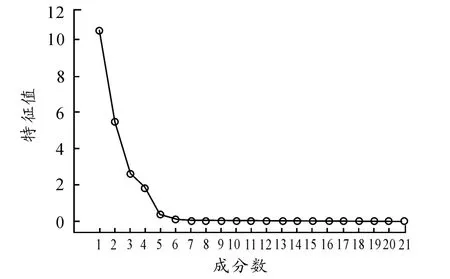
圖1 因子碎石圖

第二步:因子重命名。表3是程序生成的因子載荷矩陣，是因子分析里面最重要的內容之一。

根據表3，可建立如下因子分析模型:

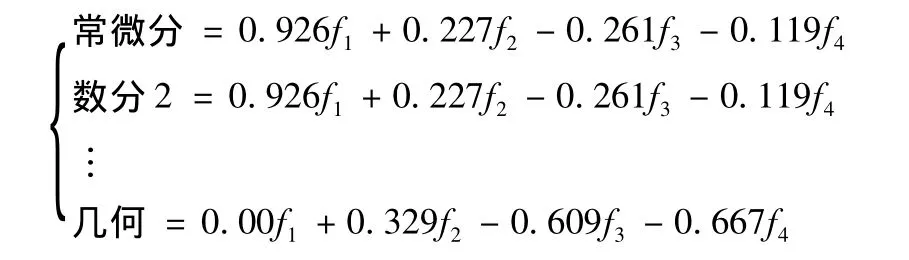
由于表3載荷看出，21個原始變量盡管在部分公因子上的載荷很高，存在較高的相關程度，但有的因子與原始變量相關性很小，對此沒有顯著的解釋作用。此外，這4個公因子實際含義比較模糊，不容易定義。因此，需要對因子載荷矩陣進行正交旋轉，使得因子更容易定義。旋轉后的因子矩陣如下(見表4)。

在表4中可以看到前7個原始變量在因子1上的載荷較高，則因子1主要解釋這7個變量。根據該7門課程的特點，可以定義因子1為數學基礎功底;因子2則主要解釋第8到第13個原始變量，反映英語成績，可以定義因子2為英語綜合水平;因子3則主要解釋第14到第18個原始變量，根據這5個變量的特點，可以定義因子3為政治綜合水平;因子4則解釋最后3個變量并可以理解為代數綜合能力。表5是對4個因子得分情況的計算。

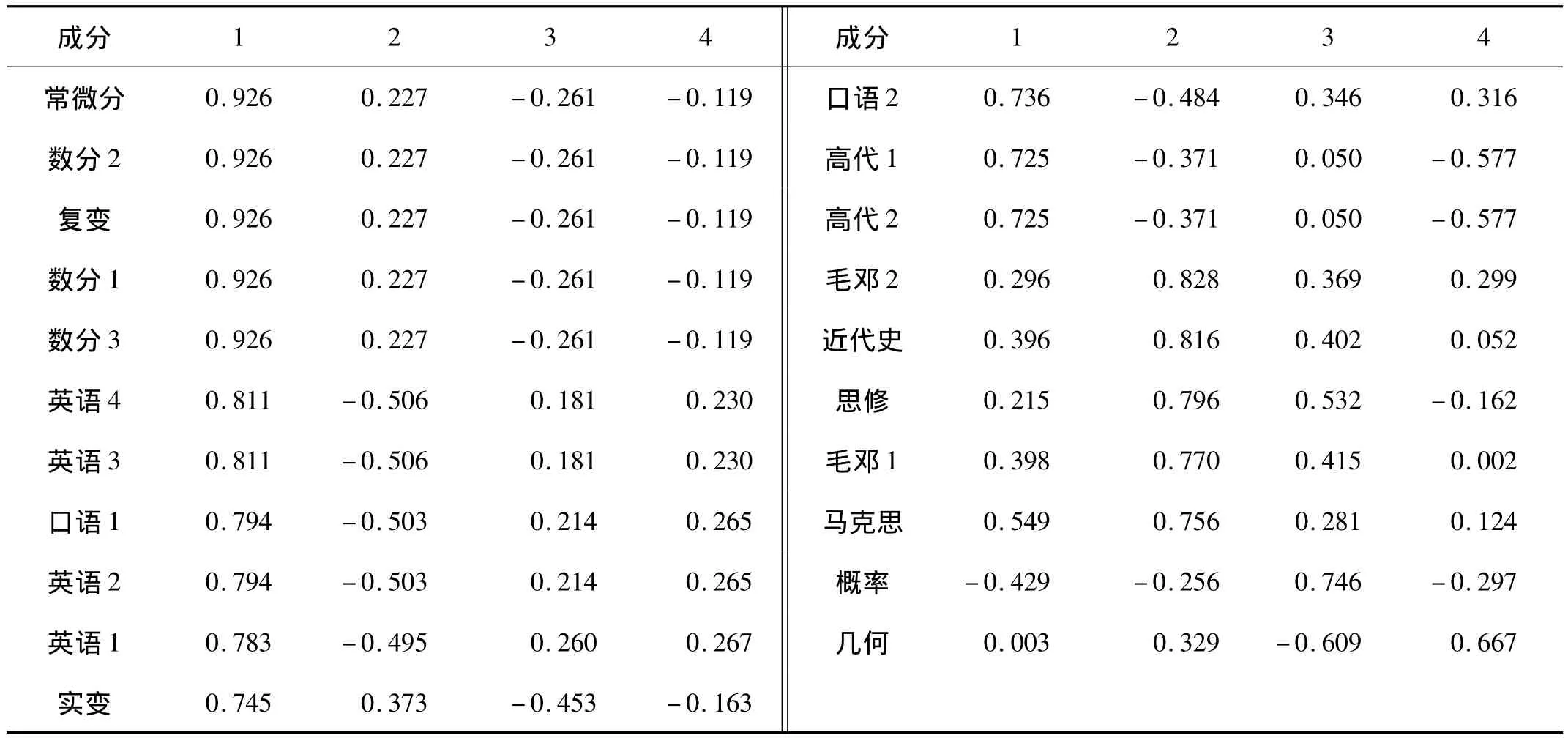
表3 因子載荷矩陣

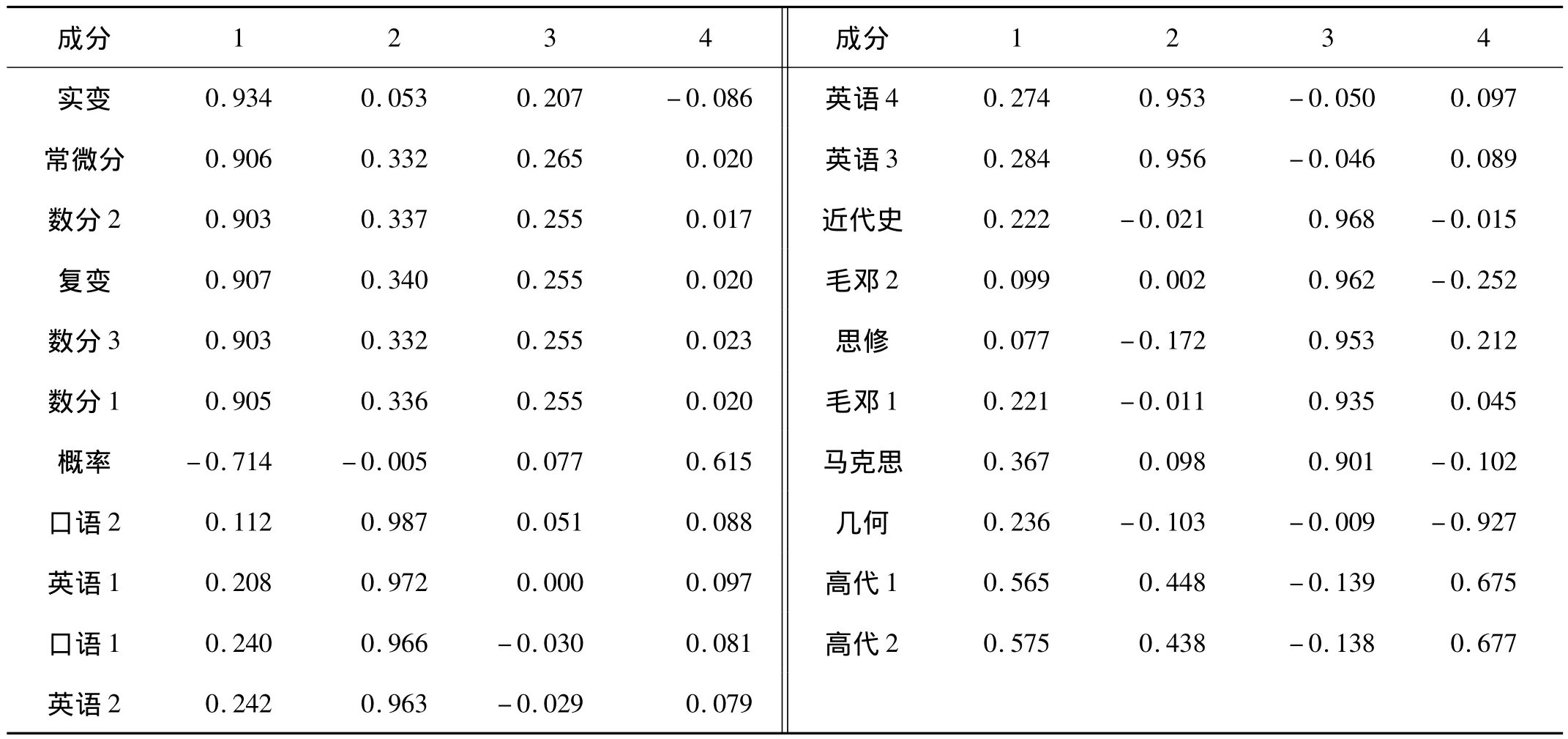
表4 旋轉后的因子載荷矩陣

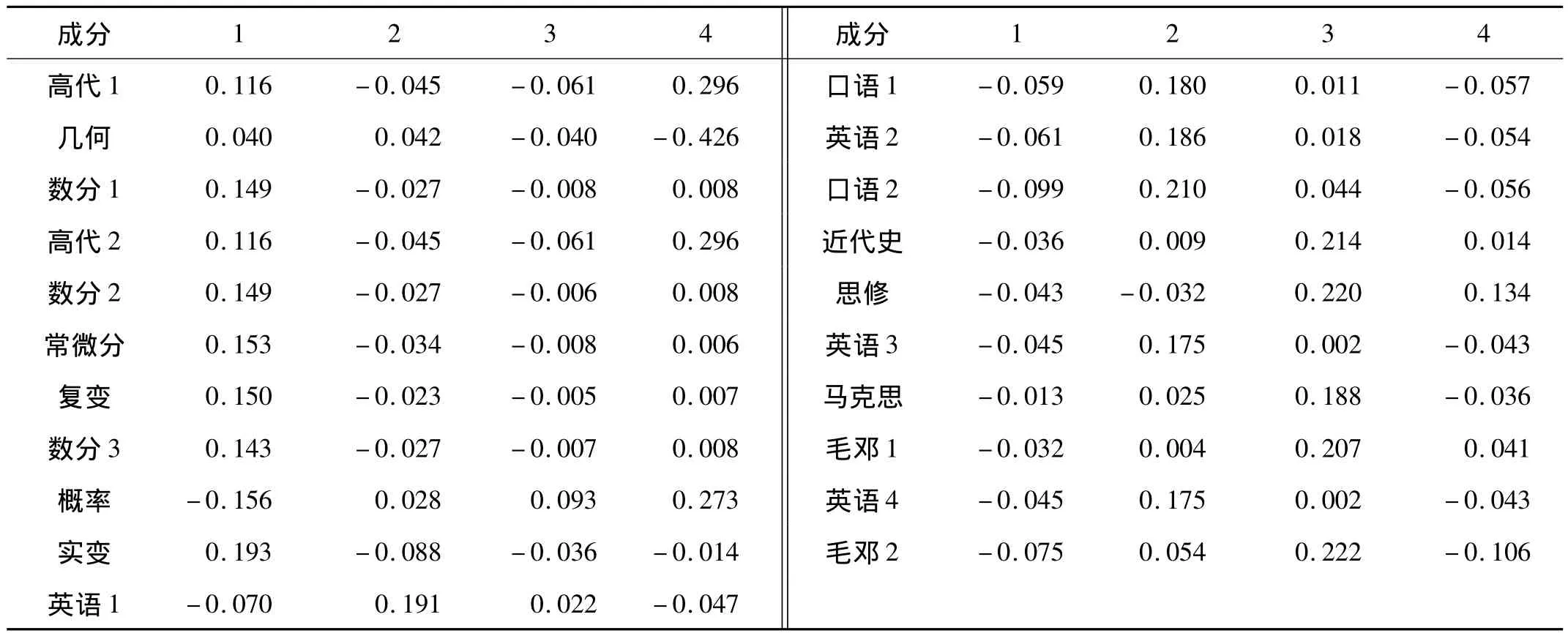
表5 成份得分系數矩陣

根據表5可得出4個因子的得分函數為:

表6 因子協方差矩陣

最后，給出了4個因子的協方差數據，見表6。提取的4個公因子不存在線性相關性，本節做的因子分析實現了設計目標。通過因子分析可得與考研成績相關的21門課程可提取不共線性的因子，并進行重新命名為:數學基礎功底、英語綜合水平、政治綜合水平和代數能力。

四、結束語

本文在《高校學生分層培養的統計分析模型》的基礎上主要是對第一類學生的成績進行因子分析。通過分析得到，在與考研成績成正比相關的各科成績中，有很多課程存在顯著的共線性。在盡可能少的減少信息損失和盡可能大幅度的降低維數的原則下，將該類學生21個指標變量成功有效的降為4個因子。提取的4個因子可以很好地解釋這21門課程，并可以較為清晰的被重命名定義為該類學生4方面的綜合素質。在學生備考期間，可以為考生在學習計劃制定中提供科學有效的參考依據，學生可以有意識、有針對性的提高自己這4方面的素質;學校方面，針對該類學生，可以制定相應的培養方案。

［1］蘇斌，謝友芹.統計分析在學生成績評估中的應用［J］.系統工程理論與實踐，2006(7):134－140.

［2］潘文浩.基于SPSS的大學生綜合測評成績分析研究［J］.吉林省教育學院學報，2010，26(9):90 －92.

［3］周興華.基于主成分分析的中原城市群城市發展水平研究［J］.重慶科技學院學報，2012(9):83 －84.

［4］章文波，陳紅艷.實用數據統計分析及SPSS 12.0應用［M］.北京:人民郵電出版社，2006.

［5］林海明，張文霖.主成分分析與因子分析的異同和SPSS軟件［J］.統計研究，2005，3(3):65 －69.

［6］陳慧琴，高月紅.主成分聚類分析法在大學生綜合測評中的應用［J］.高效管理研究，2010(26):80－81.