人字形微型樁內力計算方法

施艷秋，鄭靜，呂昌明

(1.中國鐵道科學研究院研究生部，北京100081;2.中鐵西北科學研究院有限公司，甘肅蘭州730000; 3.蘭州交通大學，甘肅蘭州730070)

人字形微型樁內力計算方法

施艷秋1，2，鄭靜2，呂昌明3

(1.中國鐵道科學研究院研究生部，北京100081;2.中鐵西北科學研究院有限公司，甘肅蘭州730000; 3.蘭州交通大學，甘肅蘭州730070)

基于彈性地基梁的微型樁內力計算方法中有一種是假定上部為鋼架，滑面處為固定支座，傳遞彎矩和剪力，滑面以下樁體按彈性地基梁法計算。本文所選微型樁同樣采用組合結構計算，同時考慮滑面處變形協調，把彈性地基梁的位移和轉角作為上部結構的支座位移，考慮位移對內力的影響。針對微型樁滑面處彎矩，基于FLAC3D程序，建立簡化的微型樁數值計算模型，提取樁的內力并繪制彎矩圖，數值模擬結果與考慮變形協調后的彎矩圖更接近。

微型樁 內力分析 變形協調 數值模擬

微型樁組合結構作為邊坡防護的一種輕型支擋結構，由于其施工安全便捷，對環境適應性強，因此在中型和小型坡體病害防治中應用較廣。微型樁通常以組合結構出現，常用的排架微型樁組合是將一組一定間距的微型樁用頂梁連接起來共同受力，但因微型樁平行布置而受力較差。針對這種情況，研究提出了人字形微型樁新結構。人字形微型樁加固邊坡類似于樹根布置，同等條件下與排架微型樁比較，其結構整體性與抗彎性能較好，變形較小，承載能力較高。目前微型樁的理論研究落后于工程實踐。在內力計算研究方面，馮君等［1］將微型樁體系和樁間巖土體視為樁—巖土體復合結構，建立了分析模型并加以計算。肖世國等［2］按彈性地基梁理論對微型樁滑面上下部分別用m，k法進行了計算分析，未考慮滑面處變形協調，認為可以忽略處理。肖維民［3］對微型樁加固順層邊坡進行研究，并建立了微型樁平面剛架受力模型。孫宏偉等［4］總結了微型樁組合結構布置形式，并按樁土作用原理在彈性地基梁理論基礎上提出了組合結構的計算公式。前述理論計算中，結構上半部在滑面處視為固定端是不完全恰當的，微型樁作為一種柔性支護結構，樁體在滑面處變形較大，不能忽略處理。本文在考慮滑面處樁身變形協調的前提下，通過內力計算公式推導、實例計算與數值模擬對比分析，研究人字形微型樁的內力。

1 理論研究

微型樁結構采用傾角為α的人字形布置，樁頂到滑面處的距離為h1，滑面上部結構受到均布荷載q的作用，計算簡圖如圖1所示。為方便理論推導做如下規定與假設:①人字形微型樁簡化為滑面以上受矩形分布荷載的剛架，滑面以下為受橫向變形約束的彈性地基梁;②考慮樁間土對力的傳遞，假定微型樁的前后樁橫向受力條件相同，荷載大小成倍數關系;③樁和土體的變形均是線彈性的，滿足小變形假設以及Winkler彈性地基梁假定［5］;④不計樁體自重、樁底反力、樁與巖土間側向摩擦力。第一步首先采用結構力學力法原理推導上部結構內力，求出滑面處彎矩和剪力。第二步根據彈性地基梁理論推導下部結構的內力計算公式，將第一步計算結果彎矩和剪力代入下部彈性地基梁公式，求出滑面處的位移和轉角。第三步推導在支座位移條件下，上部結構的內力計算公式，將第二步計算結果位移和轉角代入支座位移公式求出上部結構內力，并與外荷載作用下的結構內力進行疊加。

圖1 上部結構簡化

上部根據結構力學求解三次超靜定［6］，解出滑面處1#樁的彎矩和剪力

2#樁的彎矩和剪力

式中，n為推力傳遞系數，其余參數見圖1。

滑面以下按初參數法計算樁身內力，局部彈性地基梁的基本微分方程為

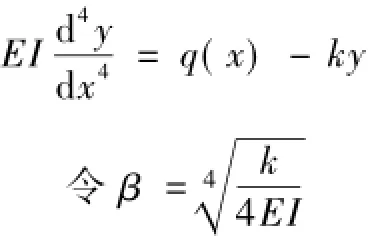
代入上方程，方程可改寫為如下形式

方程的通解為

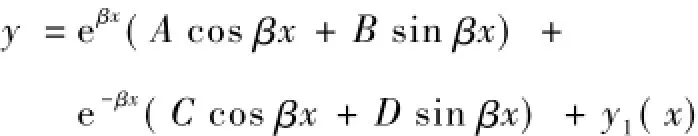
式中:EI為抗滑樁抗彎剛度，β是地基梁的特征系數，k為地基系數，y1(x)是方程的一個特解。無載段q(x)為0，特解y1(x)=0。初始截面的4個參數撓度、轉角、彎矩和剪力就叫做初參數。初參數法的基本思路是把4個積分常數改用初參數表示，初參數方程如下

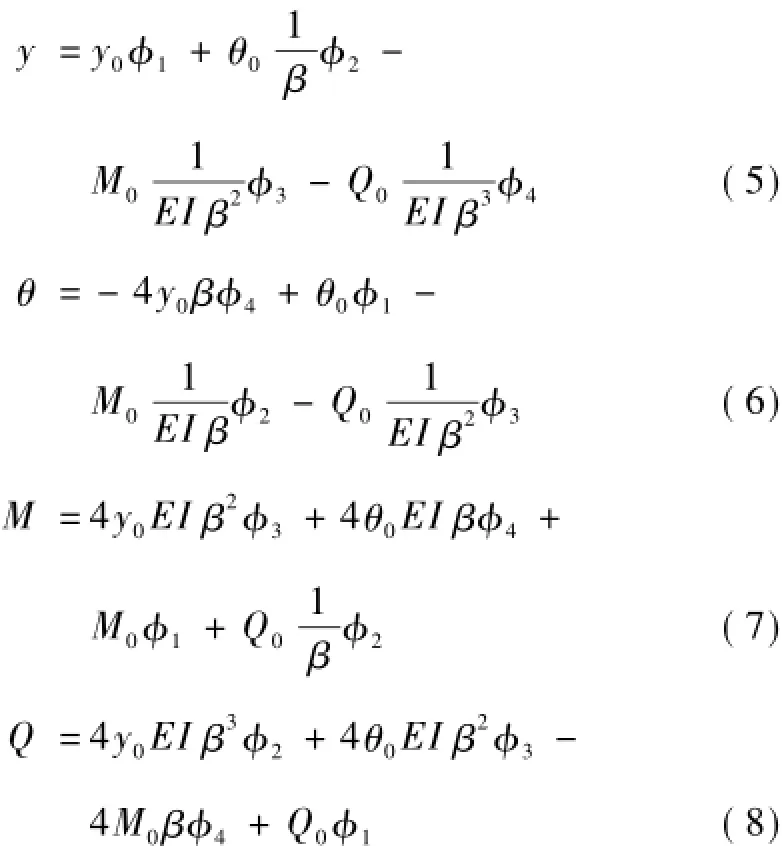
式中:φ1，φ2，φ3，φ4是為進一步簡化公式定義的克雷洛夫函數，表達式為

樁底的邊界條件分為兩種情況，第一種情況樁底為土層，按照自由端條件取彎矩和剪力為0;第二種情況，樁底嵌入巖層，按照固定端條件取位移和轉角為0。選定樁底為土層，按滑面處樁身中心為坐標起點x=0，沿樁身中心向下為x軸正方向，則樁底端點邊界條件為

代入初參數方程(7)和(8)，聯立兩方程，令φi(βl)=φil，可解得滑面處樁身撓度y0和轉角θ0為

將第一步根據上部結構求出的1#樁和2#樁滑面處的彎矩和剪力，作為初參數M0和Q0代入求出其余兩個初參數y0，θ0，代入初參數方程(5)～(8)就可以得到滑面以下任意樁長處的撓度、轉角、彎矩和剪力。再推導支座位移條件下結構的內力:對人字形剛架超靜定結構進行支座約束解除，代之以未知力X1(1#樁支座水平力向左)、X2(1#樁支座彎矩逆時針)、X3(2#樁支座彎矩順時針)，形成基本體系。設y1x，θ1表示1#樁支座的水平方向位移和轉角，方向與未知力相同，y1y表示1#樁支座豎向位移，方向向下;設y2x，θ2表示2#樁支座的水平方向位移和轉角，水平位移方向與支座反力相同，轉角方向與未知力X3方向相同，y2y表示2#樁支座豎向位移，方向向下。則力法補充位移方程可以寫為下式。

式中，Δ1c，Δ2c，Δ3c則分別代表基本結構上由于支座位移移動所引起的沿X1，X2，X3方向的位移。具體為

式中，y1，y2是根據彈性地基梁計算求出的樁頂撓度。基本結構在支座位移條件下補充位移方程如下

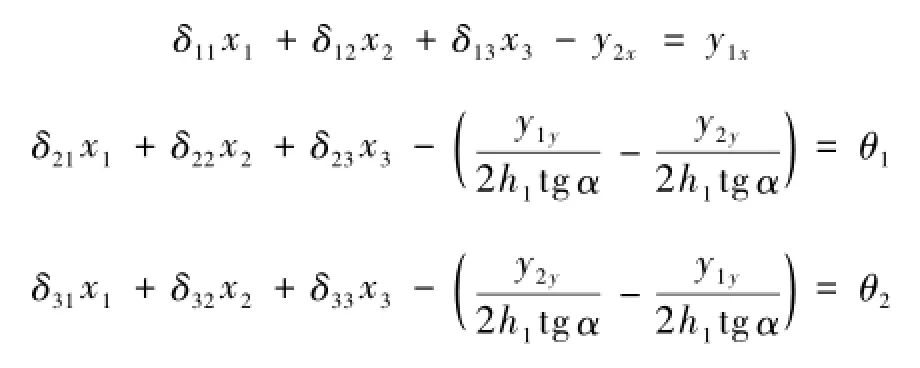
經過消元和回代，得到方程組的解

將支座反力轉化為滑面處樁上的剪力和彎矩

將支座位移條件下結構內力與荷載作用下結構內力疊加，得到協調變形后的內力圖。

2 實例分析

實際邊坡作用在樁上的推力復雜，現簡化樁后荷載為矩形分布［7］，具體參數設置如表1所示。代入理論推導公式求出上部結構內力，再將滑面處彎矩和剪力代入下部彈性地基梁，應用初參數法計算得到的滑面處位移作為支座位移施加到上部結構。再進一步計算由此產生的上半部分樁體內力，將其與之前外荷載作用下樁體內力疊加得到考慮滑面處樁體位移后的上部結構內力。經調整后的內力值理論上更趨近于真實結構內力，將其代入下部結構，重復初參數法，可再一次得到滑面處的樁體位移，再計算下半部分內力和位移。比較前后兩次內力的差值，若其滿足精度要求，即可停止計算，否則繼續迭代計算，直到滿足精度要求為止。根據彈性地基梁理論，滑面以下按初參數法計算時，滑面處按自由端處理計算出的位移和轉角比實際值大，應該折減后再作為支座位移代入上部結構。折減系數根據具體參數確定，保證支座位移對上部結構彎矩的影響不大于荷載對結構彎矩的影響，經有限次循環內力差值滿足精度要求為止，這一過程可以編程來實現。本次計算采用C語言編程，運用雙重循環首先確定滿足要求的折減系數，再輸出有限次循環后的彎矩和剪力。

表1 參數設置

調整位移前后A樁和B樁的內力見圖2和圖3。

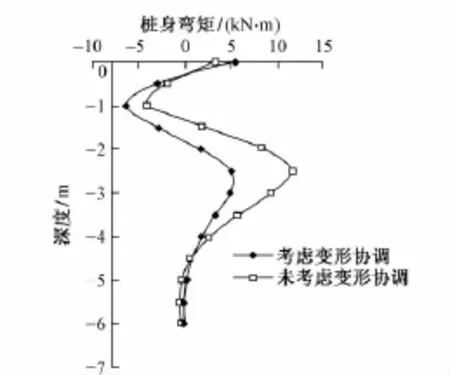
圖2 1#樁彎矩

圖3 2#樁彎矩

從理論推導結果可以看出:①1#樁考慮滑面位移時的彎矩值比不考慮位移時減小81%，樁身彎矩考慮位移后明顯減小，現場試驗結果1#樁滑面處彎矩趨近于0，若不考慮變形協調理論計算與現場試驗相差較大。人字形結構有傾角，協調變形后部分剪力轉化為軸力，會使彎矩和剪力減小。②2#樁頂點處彎矩值增大，樁身整體彎矩值呈減小趨勢，考慮支座位移時相當于放松滑面處約束條件，允許滑面處發生微小位移，樁身的彎矩將減小，上半部結構作為鋼架考慮，變形對鋼架內力影響較大，剛節點處的內力增大。

3 數值模擬

理論計算受假定條件限制，數值模擬可以將多種因素同時考慮到模型中且計算方便，在工程領域應用越來越多［8］。建立FLAC3D有限差分數值模擬，計算模型見圖4。

圖4 微型樁模型

模型分為上下兩部分，上部為滑坡體，下部為穩定土層，滑面以上樁長2 m，滑面以下樁長4 m。具體參數設置如表2所示。約束穩定土層底部X，Y和Z三個方向位移，其他邊界約束X和Y方向位移，土體采用Mohr-Coulomb彈塑性模型，微型樁采用樁結構單元模擬，每根樁由30個子單元構成，兩根樁頂部剛結。為使數值模擬與理論推導具有可比性，要控制施加到樁上力的分布形式與大小，在右側樁滑面以上施加與理論推導相同的均布力。

表2 土體和樁體參數

微型樁半徑取0.15 m，計算后提取樁單元的彎矩值并繪出彎矩圖，數值模擬結果與理論計算對比分析。彎矩圖見圖5和圖6。

圖5 1#樁彎矩

圖6 2#樁彎矩

1)1#樁數值模擬彎矩圖和調整位移后的彎矩圖變形趨勢更接近，數值模擬比理論推導結果略小，理論計算假定推力直接作用在剛架上與實際情況相差較大，數值模擬中土體摩擦力要消耗一部分推力。

2)2#樁數值模擬結果比協調變形后的彎矩值大，理論推導時2#樁的力是通過剛節點傳過去的，數值模擬除了頂部剛節點傳遞力還通過土體變形傳遞一部分力。

4 結論

1)人字形新結構的理論推導，采用上部結構簡化為剛架，下部采用彈性地基梁理論，并考慮了滑面處的位移。推導了相應計算公式，并代入具體參數，分析了支座位移對彎矩的影響。

2)建立簡化數值模型，1#樁彎矩圖與考慮變形協調后的彎矩圖變形趨勢一致，2#樁比理論計算結果大，數值模擬考慮了樁間土的影響，理論計算未考慮。

3)人字形新結構的理論計算方法目前研究較少，本文對新結構內力的理論研究和數值模擬，可給微型樁的內力理論分析提供參考。

［1］馮君，周德培，江南，等.微型樁體系加固順層巖質邊坡的內力計算模式［J］.巖石力學與工程學報，2006，25(2):284-288.

［2］肖世國，鮮飛，王喚龍.一種微型樁組合抗滑結構內力分析方法［J］.巖土力學，2010，31(8):2553-2560.

［3］肖維民.微型樁結構體系抗滑機理研究［D］.成都:西南交通大學，2005.

［4］孫宏偉.剛性帽梁微型樁組合結構內力分析［D］.成都:西南交通大學，2007.

［5］龍馭球.彈性地基梁的計算［M］.北京:高等教育出版社，1981.

［6］李廉錕.結構力學［M］.4版.北京:高等教育出版社，2004.

［7］劉凱，劉小麗，蘇媛媛.微型抗滑樁的應用發展研究現狀［J］.巖土力學，2008，28(1):675-678.

［8］陳正，梅嶺，梅國雄.柔性微型樁水平承載力數值模擬［J］.巖土力學，2011，32(7):2219-2224.

Calculation method of internal forces in herringbone micropile

SHI Yanqiu1，2，ZHENG Jing2，LV Changming3
(1.Postgraduate Department，China Academy of Railway Sciences，Beijing 100081，China;2.Northwest Research Institute Co.Ltd of CREC，Lanzhou Gansu 730000，China;3.Lanzhou Jiaotong University，Lanzhou Gansu 730070，China)

Among existing calculation methods for micropiles internal force，the upper structure was assumed as a steel frame and the sliding surface as a fixed support transfering moment and shear while the lower structure as an elastic foundation beam.In this paper，the selected micropiles were calculated as a composite structure.T he deformation coordination at the sliding surface was considered，and the displacement and the rotation of the lower structure were used as those of the bearings for the upper structure.T he effect of the displacement on the internal force was studied.Based on the FLAC3D program，a simplified model was established to simulate the micropiles. T he internal force and the moment distribution were obtained with this model.W ith consideration of the deformation coordination at the sliding surface，the results were more closed to the results of numerical simulation.

M icropiles;Analysis of internal force;Deformation coordination;Numerical simulation

U213.1+52.1

A

10.3969/j.issn.1003-1995.2015.05.28

1003-1995(2015)05-0113-05

(責任審編趙其文)

2014-06-23;

2015-02-26

科研院所技術開發研究專項資金項目(20091EG123201)

施艷秋(1989—)，女，甘肅蘭州人，碩士研究生。