直線一級倒立擺的新型控制方法研究

王 杰，孔慶忠，徐祿均

（內蒙古工業大學 機械學院，內蒙古 呼和浩特 010051）

0 引言

倒立擺的穩定控制在生活和生產中的應用非常廣泛。傳統的PID控制雖然能夠完成響應，如果效果不是特別明顯，如果將小車控制器設計成模糊PID控制器，并與擺桿閉環控制進行封裝，形成一個雙閉環PID控制器，就能夠更好地實現倒立擺系統的控制。

1 直線一級倒立擺的穩定性

直線一級倒立擺系統由小車、擺桿等組成，它們之間自由連接。在進行系統穩定性分析時，一般可以應用LaSalle’s Theorem或者是李亞普諾夫穩定性理論。本文根據系統未進行矯正時的階躍響應曲線來討論系統的穩定性，利用MATLAB進行階躍響應分析，結果如圖1、圖2所示。

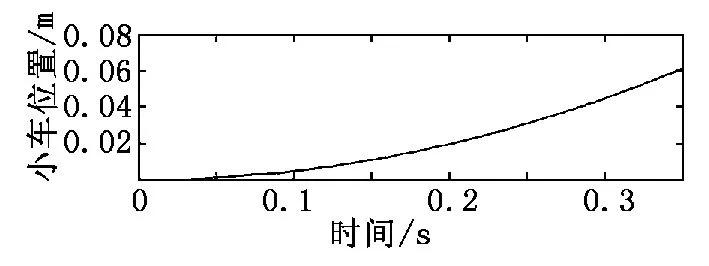
圖1 系統未矯正時小車位置的階躍響應曲線

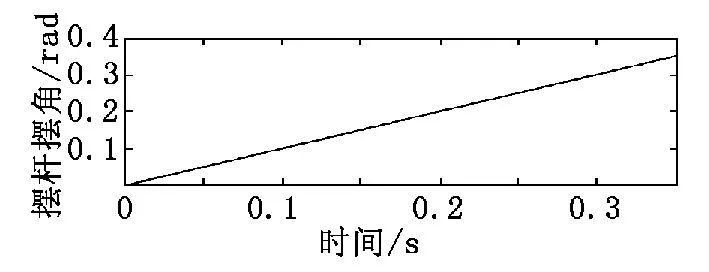
圖2 系統未矯正時擺桿擺角的階躍響應曲線

從圖1和圖2中可以看出，在階躍響應信號的作用下，擺桿的角度以及小車的位置曲線都是發散的，即在沒有使用控制器進行矯正之前，本系統在期望的平衡位置是一個非穩定系統。因此，系統需要矯正，使其變得穩定。由于直線一級倒立擺在平衡位置是能控的、可觀的，因此可以進行PID控制器設計，使系統穩定。

2 倒立擺擺桿與小車的傳統PID控制

2.1 倒立擺擺桿的傳統PID控制

把小車置于導軌中間位置，打開實驗設備，并且將擺桿手動提起置于倒立位置保持不動，然后單純對擺桿進行PID控制。根據多次實驗仿真可知：當PID控制器中比例系數Kp=30，積分系數Ki=20，微分系數Kd=2.5時，得到的仿真效果最佳。所以，將3個參數按照此值進行調節，得到的仿真曲線如圖3、圖4所示。

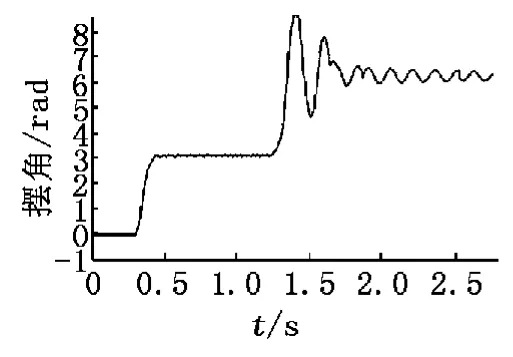
圖3 傳統PID控制 下擺桿仿真曲線

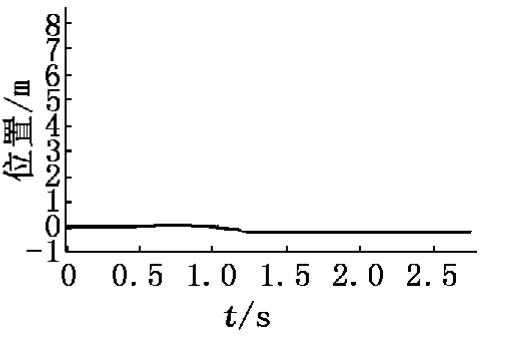
圖4 傳統PID控制下小車位置仿真曲線

在0.3s～0.5s時刻，為手動提起過程，從圖3、圖4可知，此過程中擺桿的角度不斷增加，當時間達到0.5s之后，擺桿在PID控制器的控制下能夠自動保持倒立不倒，維持平衡不倒，小車也能維持短暫平衡狀態；時間達到1.3s時，小車曲線出現突然下降，此時擺桿的角度突然增大，之后小車位置不再變化，擺桿的角度在此后出現大幅度震蕩，擺桿在重力作用下向初始位置運動，此時小車在導軌上運動到極限位置，出現阻礙后就不再運動，也就不能給擺桿倒立不倒的力；在2s之后，小車的位置保持不變，也就是處于靜止狀態，擺桿在重力作用下，由于慣性作用繼續左右擺動，能夠維持短暫的自由擺動，直至能量消耗完就靜止。所以，單獨對擺桿進行PID控制器控制，能夠達到最終目的，但是穩定效果不是特別明顯。

2.2 倒立擺小車的模糊PID控制

為保證擺桿直立運動，小車必須擁有合適的位移以及速度。但是對于由伺服電機帶動的小車來說，不能精確地給出數學模型以及傳遞函數。因此，在對擺桿進行角度檢測之后，對小車的控制采用模糊PID控制。當擺桿在直立的平衡位置范圍內擺動時，控制小車的速度及位移，使擺桿直立不倒。對于擺桿來說，起擺的速度和加速度比較大，當達到平衡位置時，加速度在較小范圍內變化。用模糊PID控制倒立擺小車得到的仿真曲線如圖5所示，此時倒立擺擺桿的仿真曲線如圖6所示。

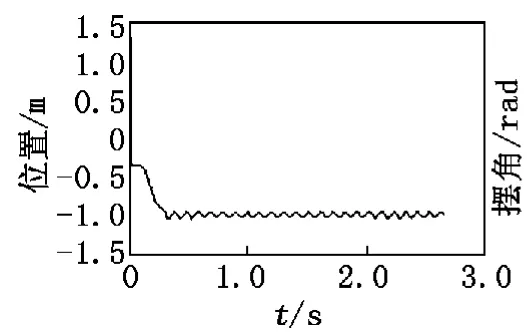
圖5 模糊PID控制下小車位置仿真曲線

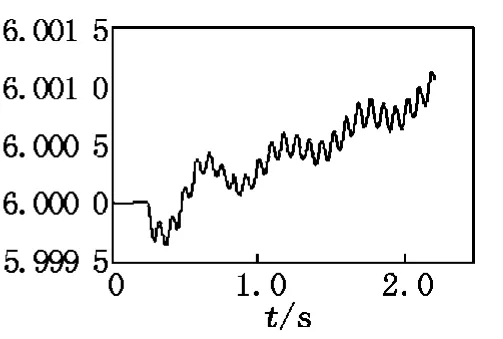
圖6 模糊PID控制 下擺桿仿真曲線

在這種單一對小車進行模糊控制的情況下，小車運動穩定，倒立擺擺桿的運動在單位時間內是穩定的，但是在整個控制過程中是不穩定的。這種控制效果雖然也能夠達到讓倒立擺擺桿倒立穩定的目的，但是，控制效果并不理想。為了能使擺桿得到更加優良的控制，實現理想的控制效果，還可以尋找更好的控制方法。

3 倒立擺擺桿與小車的新型PID控制

根據上述兩種控制進行綜合分析，單純對擺桿進行PID控制可以使系統維持短暫時間的穩定，當小車遇到極限位置時系統停止運動；單純對小車進行PID控制時，系統更加不穩定，魯棒性能效果不理想，穩定時間變得更小。因此，在上述理論的基礎上，分別將兩個控制器進行組合，形成雙PID控制組合，得到的倒立擺系統閉環PID控制器如圖7所示。利用這種雙閉環控制器，得到倒立擺的實時控制仿真曲線，如圖8、圖9所示。

從圖8、圖9可以很清晰地看到，擺桿在兩個控制器的控制下維持倒立穩定，雖然小車仿真曲線出現震蕩，但是小車可以在導軌上的某個范圍內一直運動，保證擺桿倒立不倒。本實驗仿真結果顯示：雙閉環控制器對此倒立擺系統具有很好的控制作用。

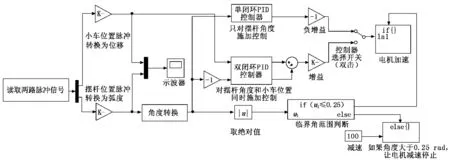
圖7 倒立擺系統閉環PID控制器

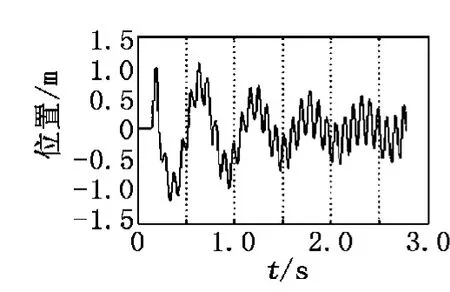
圖8 閉環PID控制下小車位置仿真曲線

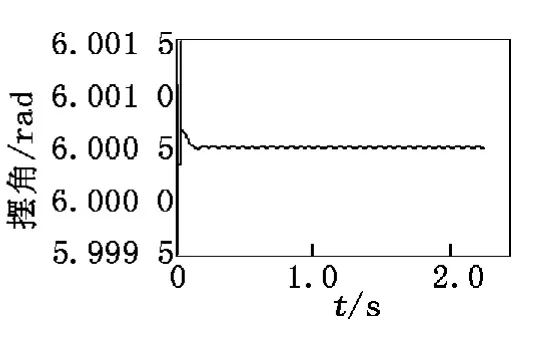
圖9 閉環PID控制 下擺桿仿真曲線

4 結論

單獨對擺桿進行PID控制器控制，能夠達到最終目的，但是穩定效果不是特別明顯。單獨對小車進行模糊PID控制，也能達到最終目的，效果仍然不是特別明顯。在分析這兩個單獨的控制器的基礎上，將兩個獨立的控制器進行組合封裝，形成一個雙閉環PID控制器，能夠很好地實現倒立擺系統的控制，最終達到理想的效果。

［1］ 黃宏格.直線倒立擺機理模型及控制性能研究［D］.長沙：中南大學，2008：5-6.

［2］ 王雪.基于小車倒立擺的自動控制原理開放性實驗的開發與研究［D］.重慶：重慶大學，2007：25-27.

［3］ 徐雄，石曙東.基于 Matlab的實時模糊控制系統的研發［J］.湖北師范學院學報，2007（3）：79-81.

［4］ 王孝莉.倒立擺智能控制系統的研究［D］.濟南：山東大學，2007：35-38.