關于N型晶體硅費米能級的研究
晶澳太陽能有限公司 ■ 王惠 楊偉強 嚴金梅 魏紅軍
0 引言
由于硅材料資源豐富且生產工藝成熟,因此晶體硅太陽電池在未來的光伏市場中仍占主導地位。而費米能級在半導硅中是非常重要的物理參數,它決定載流子的分布函數,并且直接影響硅的許多物理性質,如硅的導電性及輸運特性等[1,2],因此對于硅的費米能級的研究十分活躍[3-9]。由于硅的費米能級與溫度、雜質濃度及禁帶寬度等諸多因素有關且關系復雜,所以很難求出各種情況下的費米能級的解析解,一般情況下只在特定溫度區域內忽略某些次要因素解析求解硅的費米能級[10]。
本文采用數值方法計算定摻雜濃度下N型晶體硅的費米能級隨溫度(0~800 K)的變化規律,并討論禁帶寬度隨溫度的變化對費米能級的影響。
1 N型半導體硅費米能級的數值計算
1.1 非簡并半導體載流子分布
熱平衡下,能量為E 的量子態被電子占據的概率為[10]:
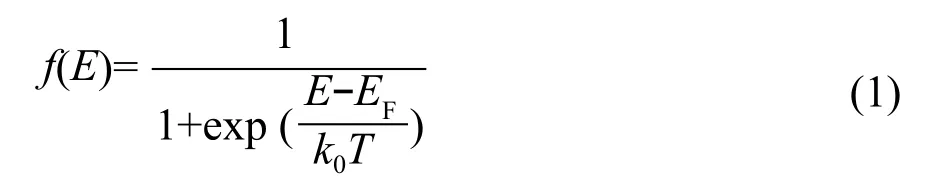
式中,k0為玻爾茲曼常數;T 為熱力學溫度;EF為費米能級;f(E)即費米分布函數。
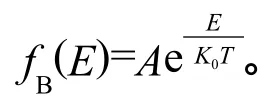
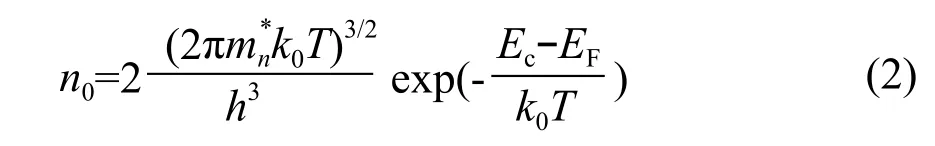
非簡并情況下,半導體價帶中空穴濃度為[10]:

脂肪含量在4.30~6.35g/100g之間,平均含量為5.67g/100g,不同部位的平均含量高低依次為臀腿肉含量5.49g/100g、后腿肉含量5.26g/100g、前腿肉含量5.01g/100g、頸肩肉含量4.52g/100g、背肌肉含量4.50g/100g。
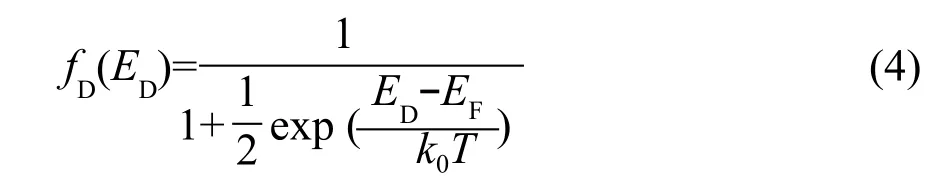
施主雜質電離濃度為:

非簡并情況下,式(6)沒有忽略任何因素,在所有的溫度范圍內均成立。顯然,式(6)是關于費米能級和溫度的較復雜的函數關系。此外,半導體的禁帶寬度Eg=Ec–Ev也是隨溫度而緩慢變化的,因此很難解析求解定摻雜濃度下的費米能級。
1.2 硅禁帶寬度隨溫度的變化
半導體的禁帶寬度并不是一個恒定的數值,而是隨著溫度緩慢變化的。硅的禁帶寬度隨溫度的變化規律為[10]:
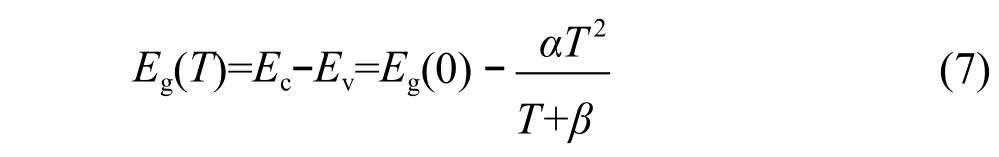
式中,Eg(0)=1.170 eV;α=4.73×10-4eV/K,β=636 K。
因為禁帶寬度呈現在式(6)的指數中,因此盡管禁帶寬度隨溫度的變化較緩慢,但對費米能級及載流子數目的影響不能忽略。
1.3 N型硅費米能級數值計算
數值求解方程組(6)和(7)。相應的計算參數為[11]:取導帶底能級Ec=0 eV,價帶頂能級Ev=1.12 eV,電子有效質量mn*=1.08m0,空穴有效質量mp*=0.59m0,硅中磷的電離能級ED=-0.044 eV,m0為自由電子的靜止質量;設摻雜濃度為ND=1016cm-3。
1.3.1 不考慮禁帶寬度隨溫度變化時的費米能級
不考慮禁帶寬度隨溫度的變化,取禁帶寬度Eg=Ec–Ev=-1.12 eV,溫度間隔取1 K時,N型硅(摻磷)費米能級隨溫度變化的曲線如圖1 所示。
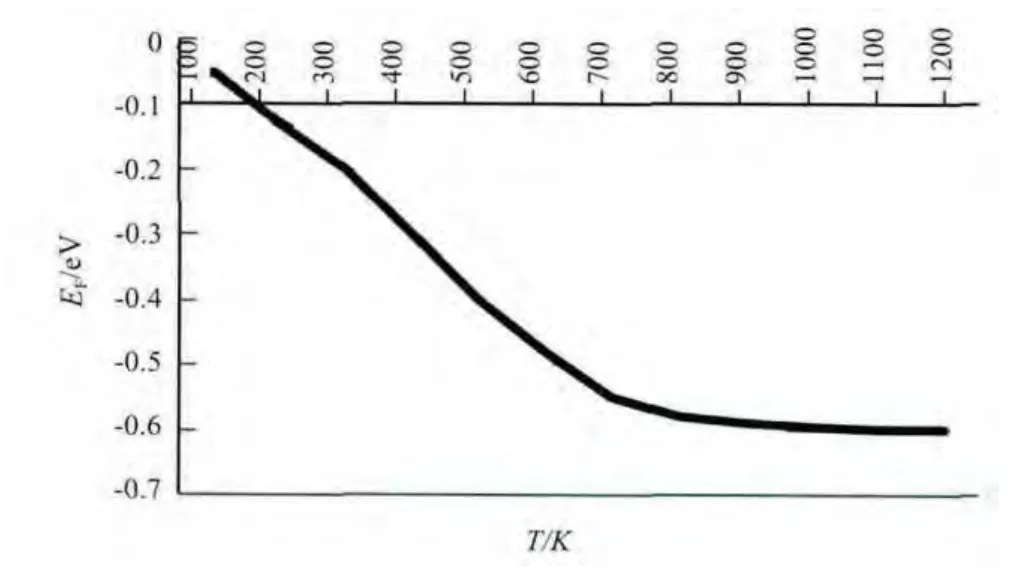
圖1 Eg為定值時的費米能級
計算結果顯示,在溫度0 K
1.3.2 考慮禁帶寬度隨溫度變化時的費米能級
考慮禁帶寬度隨溫度的變化,溫度間隔取1 K時,N型硅(摻磷)費米能級隨溫度變化曲線,如圖2所示。
計算結果顯示,在溫度0 K 圖2 Eg隨溫度變化時的費米能級 1)在溫度0 K 2)在溫度100 K 3)溫度大于700 K時,費米能級逐漸趨于平緩,接近帶隙中間,即本征半導體的費米能級,與實驗吻合。 [1] An Xingtao, Liu Jianjun. Even-odd parity oscillations in spin polarization of a quantum dot array[J]. Applied Physics Letters,2009, 95(16), 163501. [2] Sun Q F, Xie X C. Bias-controllable intrinsic spin polarization in a quantum dot: Proposed scheme based on spin-orbit interaction[J]. Physical Review, B 73, 2006, 235301. [3] 王德豐. 單摻雜及混合摻雜半導體費米能級隨溫度變化的數值計算[D]. 長春:東北師范大學, 2009. [4] 王中長, 劉天模, 李家鳴. 混合雜質半導體費米能級公式及數值計算[J]. 重慶大學學報, 2003, 26(11): 52-55. [5] 姚朋軍, 沈桂芬. Matlab 在計算半導體費米能級和載流子濃度中的應用[J]. 遼寧大學學報(自然科學版), 2001, 28(3):253-256. [6] 周亞訓. 單一雜質半導體費米能級的普適公式[J]. 大學物理, 1999, (10): 10-11. [7] 黃瑞, 馬平平. 費米能級之近似計算[J]. 首都師范大學學報(自然科學版), 1995, 16(4): 52-58. [8] 肖志雄, 鄭茳, 魏同立, 等. 重摻雜硅費米能級和少數載流子濃度的溫度特性分析[J]. 低溫物理學報, 1995, 17(2): 101-109. [9] 馬松山, 徐慧, 劉小良, 等. 無序度和溫度對一維無序體系費米能的影響[J]. 中南大學學報(自然科學報), 2007, 38(2):281-284. [10] 劉恩科, 朱秉升, 羅晉生. 半導體物理學(第4版)[M]. 北京: 國防工業出版社, 2010. [11] 黃昆, 謝希德. 半導體物理學[M]. 北京: 科學出版社,1958.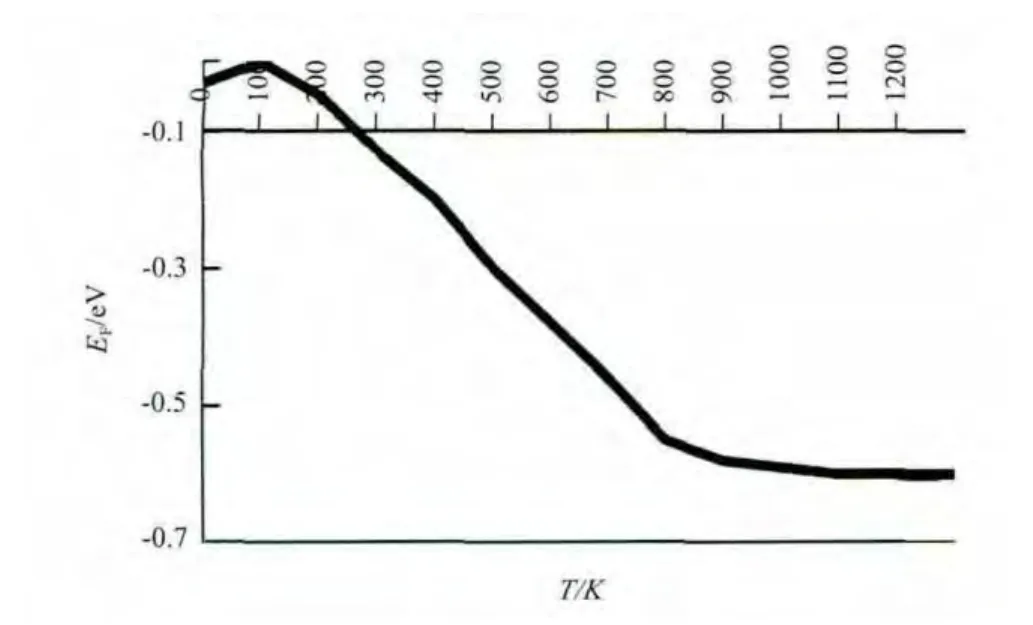
2 結論

