變式教學:讓學生的思維更活躍、更創新
?江蘇連云港市新海初級中學 熊誠燕
1 引言
由于受到“應試教育”的影響,當前數學課堂中仍然存在重講解輕思考、重問答輕交流、重記憶輕創新、重一致輕個性等問題,這些問題看似尋常,卻嚴重影響了教學質量,從而使學生越發缺乏學習積極性和主動性,更有甚者產生厭學情緒.那么,如何才能解決上述問題?筆者認為,變式教學不僅能讓上述問題得到較大緩解,還能讓學生的思維更活躍、更創新,有效訓練和培養學生的想象力和發散思維能力,促進數學學習能力的發展.下面結合自己的教學實踐,探討變式教學在初中數學教學中的有效運用.
2 變式教學的內涵
所謂“變式教學”,指的是教師有針對性地合理轉化命題,如變更非本質特征、變化問題條件或結論、改變問題的形式或內容、添置應用性的各種環境等,但無論如何變化都保留其本質因素,以促進學生在“變化”中發現“不變”的本質,從而探尋到“變化”的規律,最終獲得本質屬性的一種教學方法.
在教學中有目的地運用變式教學,為的是更好地融合相互關聯的知識,深化學生的理解,讓學生更好地識別問題本質,以培養學生分析、歸納和解決問題的能力,同時極好地抑制“題海戰術”,激起學生的學習興趣,拓寬學生的學習視野,達到輕負高效的教學效果[1].
3 變式教學的應用策略
3.1 一題多問,促進知識的建構
問題是數學的心臟,用問題巧妙地將教師情感融入教學內容,是促進學生深度學習,實現知識建構的有效途徑.然而日常教學中,大部分問題內容過于單一,對知識與能力的考查也較為片面,無法充分訓練學生的思維.倘若教師適當擴充或演變問題,采用“一題多問”的變式教學,則可以在一道習題中呈現多個知識點,溝通知識間的內在聯系,從而使得零碎、單一的知識點串成鏈、織成網,促進知識的完整建構,提高學生的綜合運用能力.
例1已知等腰△ABC的腰長為6,底邊長為8,試求△ABC的周長.
變式1已知等腰△ABC的腰長為6,周長為20,試求△ABC底邊的長.
變式2已知等腰△ABC一邊的長是6,另一邊的長是8,試求△ABC的周長.
變式3已知等腰△ABC一邊的長是6,另一邊的長是12,試求△ABC的周長.
變式4已知等腰△ABC的腰長為x,試求出△ABC底邊長y的取值范圍.
變式5已知等腰△ABC的腰長為x,底邊的長為y,周長為20,試寫出y與x的函數關系式,并作出相應的函數圖象.
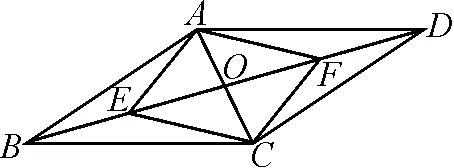
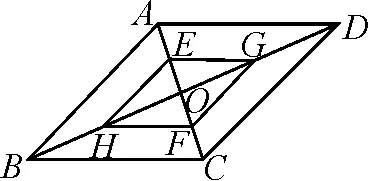
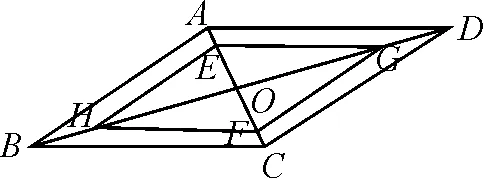
教師以例1為導引,提出一系列問題,每個問題都有其特定的目的,如變式1是為了磨礪學生的逆向思維;變式2則更進一步地進行思維策略的轉化,在分類討論中完善解題路徑;變式3是為了提升學生思維的嚴密性而設計;變式4則在要求上又更進了一步,需要學生深入理解和運用“0 在數學解題的過程中,我們常常發現,一些數學問題看似毫無關聯,卻有著相同的解題思路和解題方法.這就需要教師多番搜集整理習題,讓學生通過比較、分析、探究這些“形異質同”或“型近質同”的數學問題,領悟其中的內在聯系,牢牢把握共同的本質特征,掌握解決這一類問題的規律,促進數學思想方法的形成.通過多題歸一的變式教學,可以自然擺脫“題海”的束縛,達到舉一反三的教學效能,更好地培養學生思維的發散性和創新性. 例2二次函數的圖象經過A(-3,0),B(1,0)和C(0,-3),試求該二次函數的解析式. 變式1一拋物線過點B(1,0)和C(0,-3),且直線x=-1為拋物線的對稱軸,試求該拋物線的解析式. 變式2二次函數的圖象經過一次函數y=-x-3的圖象與x軸和y軸的交點A和C,且經過點B(1,0),試求該二次函數的解析式. 變式3一次函數的圖象經過A(1,0),且與y軸的交點為(0,-1),同時與二次函數交于點A(1,m)和B(n,4),且直線x=2為二次函數的對稱軸,試求這兩個函數的解析式. 在教學的過程中,教師在給出關鍵性的點撥之后充分留白,為學生提供獨立思考、自主探究和合作交流的時空.有了教師的適時啟發,有了思考的時空,學生深度摸索,很快探尋出解決此類問題的基本思路,即設二次函數的一般式,并利用三點法建立方程組,充分領悟解題的思想方法.這種多題歸一的變式訓練,可以引導學生把握問題本質、觸類旁通、悟出共性,從而更好地培養思維的變通性. 數學學習永無止境,想要讓學生學好數學,需要從學習興趣和思維能力的培養上下功夫.在數學教學中,教師借助典型習題,采取一題多解的變式教學方式,對學生思維的靈活性、廣闊性、探索性的培養是十分有力的.更重要的是讓學生在能力拔節的過程中品味數學解題的樂趣,使其興趣自然倍增,成就感油然而生. 例3如圖1,已知圓O外接于△ABC,圓心O在三角形的高線CD上,點E,F分別平分邊AC,BC. 圖1 證明:四邊形CEDF為菱形. 學生經過深入思考與探究,得出了以下多種證法. 圖2 同一個數學問題,由于思考角度不同,得到的思路也不同.探尋多種解題方法,可以有效拓寬解題思路,發展思維能力;遨游在數學海洋中,可以讓知識更加豐富,頭腦更加靈活.以上一題多解訓練,涉及多個數學知識的綜合運用,學生在多解的過程中完成了知識的融合,同時進一步分析各種證法,可以讓學生發現各種證法間的聯系,收獲成功的喜悅. 教師實施變式教學,目的不僅僅在于一個問題的解決,而在于通過解決一個問題融通一類問題,達成思路的拓展,培養數學探究能力.數學教學中,教師需要深度探究課本例習題,善拓展,常更新,從課本例習題出發延伸變式,得出各種新問題,以此為載體培養學生思維的遷移能力[2]. 例4如圖3,已知平行四邊形ABCD中,點E,F分別平分邊OB,OD,那么四邊形AECF是否為平行四邊形?請說明理由. 圖3 變式1如圖4,已知平行四邊形ABCD中,點H,G,E,F分別平分BO,DO,AO,CO,那么四邊形EHFG是否為平行四邊形?若是,請判斷EG,FH的位置關系;若不是,請說明理由. 圖4 變式2如圖5,已知平行四邊形ABCD中,點E,F在對角線AC上,點G,H在對角線BD上,且有AE=CF,DG=BH,那么四邊形EHFG是否為平行四邊形?請說明理由. 圖5 借助有價值、有深度、有思維含量的變式訓練,通過“變”的過程引導學生去思考、去探索、去挖掘、去創造,深化對平行四邊形判定定理的理解與應用,讓思維得到鍛煉與發展,提高數學探究能力. 總之,變式訓練的合理利用不僅有利于學生思維能力的提高,還可以培養學生勇于質疑、勤于探索、善于創造的品質[3].教師的教育智慧決定了教學理念的貫徹程度,教師需要理論與實踐相融合,借助變式教學這一“利器”,讓學生的思維更活躍、更創新,培養出新課程理念需要的人才.3.2 多題歸一,滲透數學知識的內在聯系
3.3 一題多解,品味解題的樂趣
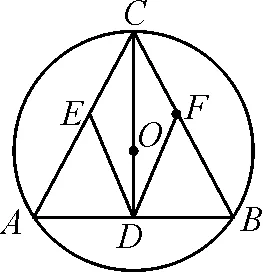
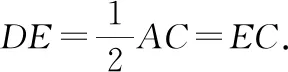

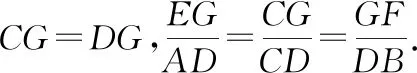
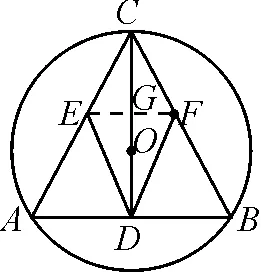
3.4 一題多變,培養思維的遷移能力
4 結語

