大直徑帶轂直齒輪冷精密成形數值模擬及工藝分析

汪金保，劉華，孫紅星，劉百宣，王濤

（1.鄭州機械研究所，鄭州450052;2.鄭州大學機械工程學院，鄭州 450052）

帶轂直齒輪是一種常見的齒輪類零件，其傳統的制造方法為鍛造制坯后切削加工齒部［1—2］。與傳統機械加工相比，冷精密塑性成形具有節能、節材、高產、優質等顯著優點，可以使材料的組織致密均勻，金屬流線分布均勻合理，顯著提高鍛件的耐蝕性、耐磨性、抗彎曲性和疲勞性能［3—5］。關于直齒輪精鍛的研究工藝比較多，小模數齒輪精鍛已經在實際中得到應用［6—7］。文中通過數值模擬研究了大模數大直徑帶轂直齒輪，根據帶轂齒輪特點提出新的工藝，以期為實際生產提供指導。

1 零件的工藝分析

齒輪齒數Z=30，模數m=5，齒頂圓直徑160 mm，齒輪上下兩端面凸臺高度不同。齒輪零件圖如圖1所示，該齒輪具有以下特點:高徑比小于0.5，屬于扁平齒輪;上下不對稱;大直徑大模數;齒輪由外齒部、中間輪輻和內部凸臺三部分組成。由于齒輪零件非常復雜，采用整體式沖頭成形非常困難，因此為了成形的可行性，尋求恰當的沖頭結構是成形本齒輪的關鍵。

圖1 帶轂直齒輪零件結構示意圖Fig.1 Part structure schematic of spur gear with hub

1.1 關鍵難點

1）如何減小載荷降低模具應力。目前的技術能夠鍛造出小模數小直徑的齒輪或者高徑比很大的齒輪，對大模數大直徑齒輪尚無比較好的鍛造工藝，由于冷擠壓需要很大載荷，模具承受單位應力很大，往往不能達到實際生產要求。

2）如何成形出高精度齒輪。冷精密塑形成形就是在無切削或少切削的條件下鍛造出高精度齒輪。

1.2 解決齒輪成形基本方法

1）基于分流減壓原理。20世紀80年代，日本學者將分流鍛造思想引入齒輪成形中，提出孔分流和軸分流2種分流方法，后人不斷發展和完善分流思想，使得冷精密成形成為可能［8—10］。

2）多工步成形。對于大直徑大模數齒輪，采用局部多工步成形可以減小模具載荷，降低模具應力。

3）雙向擠壓齒輪。雙向墩擠齒輪可以減小齒輪成形載荷，減小模具應力［11］，并且可以產生有利摩擦，使得齒形角隅處容易充滿。

4）輪齒修復理論。對齒形凹模彈性變形和鍛件彈性回復進行研究，可以得到高精度齒輪［12—14］。

2 工藝方案的提出

根據圖1齒輪的形狀特點，先采用整體沖頭和2層沖頭分別模擬分析了齒輪，發現很難成形目標齒輪鍛件。通過將沖頭分為內、中、外3層成形具有較好效果，其模具結構如圖2所示，其中內沖頭主要的作用是成形齒輪凸臺和上面的孔，中沖頭成形幅板部分，外沖頭成形齒形部分。本研究的目的是生產壓機進行聯動控制成形，也可通過多工位成形。

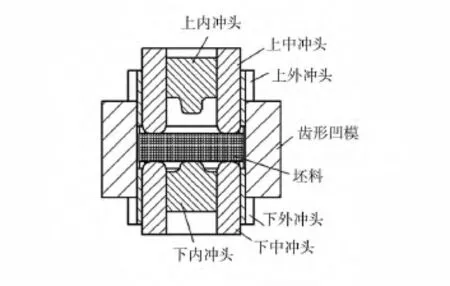
圖2 模具結構圖Fig.2 Mold structure of spur gear with hub

坯料為棒料，尺寸為φ132 mm×35 mm。采用上下各3層沖頭，根據各模具沖頭運動情況，提出3種方案進行優化選擇。

方案一:Ⅰ上中沖頭向下擠壓25 mm;Ⅱ上中沖頭向上退6 mm，下內沖頭向上頂3 mm;Ⅲ上內沖頭向下擠壓20 mm;Ⅳ上下外沖頭對擠。如圖3所示，圖3方案一中展示4個階段末示意圖。

方案二:Ⅰ上中沖頭向下擠壓25 mm;Ⅱ上中沖頭向上退6 mm，下內沖頭向上頂3 mm;Ⅲ上下外沖頭對擠;Ⅳ上內沖頭向下擠壓20 mm。

方案三:Ⅰ上中沖頭向下擠壓25 mm;Ⅱ上下外沖頭同時對擠;Ⅲ上內沖頭向下擠壓20 mm。

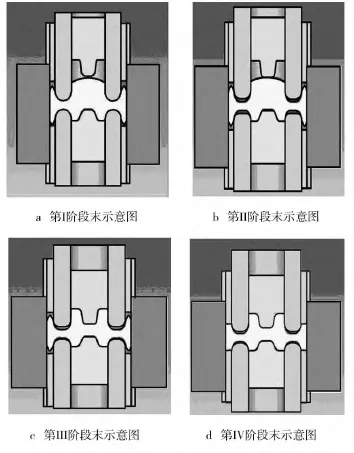
圖3 方案一4個階段示意圖Fig.3 A schematic diagram of the four stages for scheme 1

3 工藝方案數值模擬

采用Solidworks軟件建模，繪制坯料和各沖頭三維模型并確定位置關系進行裝配，將三維裝配體保存為STL文件格式，然后將這些文件直接導入Deform-3D軟件中，設置參數對3種工藝方案進行模擬。

3.1 模擬條件設定

成形過程為冷擠壓，溫度為常溫20℃，熱力耦合系數為5。材料為Deform材料庫 AISI-5120，COLD（20Cr）。由于擠壓為體積成形，采用剪切摩擦模型，摩擦因子為0.12。不考慮模具彈性變形，設定模具為剛性;坯料設定為剛粘塑性模型。采用完整坯料進行模擬，網格采用絕對網格劃分方法，最小尺寸為1 mm，最大尺寸為2 mm，尺寸比率為2。沖頭模具運動速度為20 mm/s。

3.2 3種方案載荷-時間曲線

為了更加清楚地看到各運動沖頭載荷情況，對方案一、二、三的載荷時間曲線進行簡化改動，去除了各階段受力較小的非運動沖頭。如圖4所示，圖4a方案一中Ⅰ，Ⅱ，Ⅲ，Ⅳ四區分別對應圖3方案一4個運動階段;圖4b方案二和圖4c方案三類似。

3.2.1 方案一和方案二對比分析

方案一和方案二均有4個階段，前2個階段相同，不同的是對第Ⅲ階段和第Ⅳ階段擠壓順序進行調換。模擬分析上下外沖頭和上下內沖頭擠壓順序對載荷影響，從圖5中可以看出方案一和方案二各沖頭載荷位移曲線基本重合。由表1方案一和方案二各沖頭載荷和位移參數值對比，可知方案一和方案二沖頭位移差值小于0.3%，可認為擠壓到相同位移;載荷峰值最大差值百分比小于4%。可以認為方案一和方案二中第Ⅲ階段和第Ⅳ階段調換加載順序對載荷無影響。說明在有輪轂分流腔時，鍛件上內凸臺有無接觸對齒形成形載荷的影響可忽略。

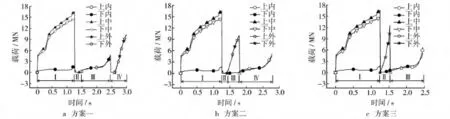
圖4 3種不同方案的載荷-時間曲線Fig.4 The load-time curves of the three different schemes

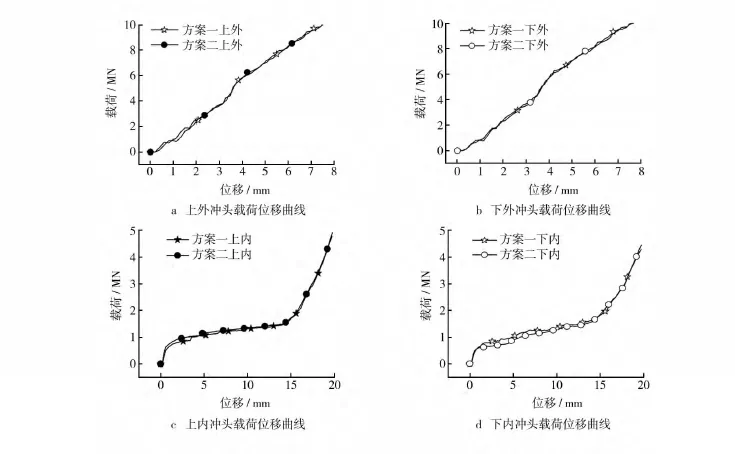
圖5 方案一、二各沖頭載荷位移曲線Fig.5 The load-displacement curves of different punches in schemes 1 and 2

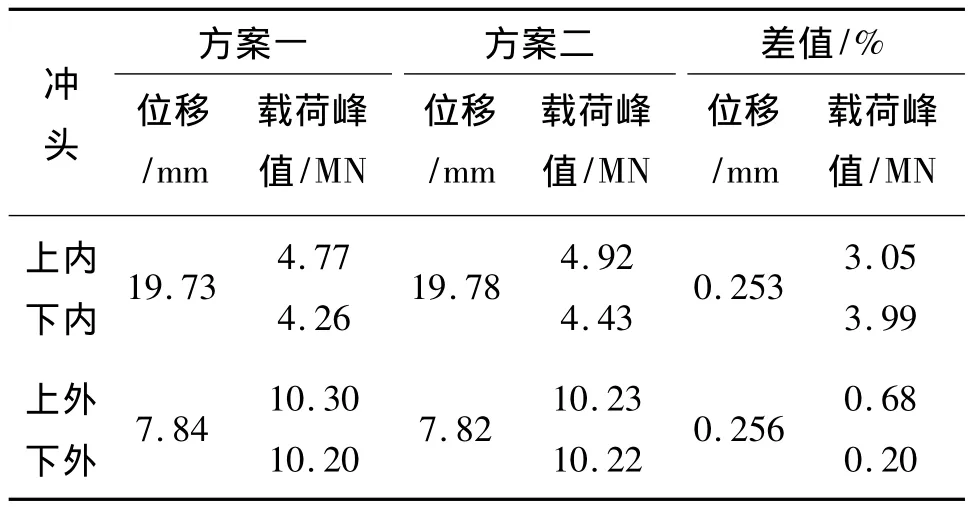
表1 方案一和方案二的參數值Table 1 The parameter values of schemes 1 and 2

3.2.2 方案二和方案三對比分析

與方案二相比，方案三中缺少方案二中第Ⅱ階段形成輪轂中分流腔階段。方案二和方案三對比可以分析出中分流腔對載荷影響的大小。由圖6方案二和方案三各沖頭載荷-位移曲線可以看出，輪轂中分流腔對載荷影響比較大。對圖6載荷-位移進行對比如表2所示。從表2中可以看出，與方案二相比，方案三上內沖頭載荷峰值增加35.8%，下內沖頭載荷峰值增加16.5%，上外沖頭載荷峰值增加22.6%，下外沖頭載荷峰值增加17.5%。并且方案三上下外沖頭位移差值減少41.9%，上內沖頭位移減少7.38%。這是由于方案三輪轂處無分流腔，隨著上下外沖頭載荷加大只有很少一部分金屬流到上內凸臺處，造成方案三上下外沖頭位移減小。對比方案二和方案三可知:輪轂中分流腔對載荷影響很大，方案二能大幅度減小載荷;在有輪轂中分流腔的條件下，上內凸臺分流作用很小;在方案三條件下，如果先擠壓上內沖頭，再擠壓上下外沖頭，可以預測齒形載荷會進一步增大。

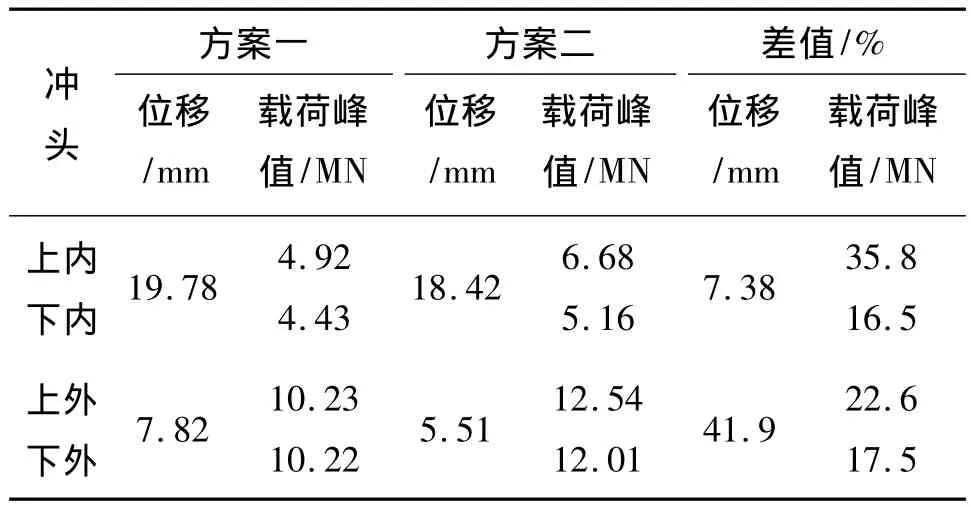
表2 方案二和方案三參的數值Table 2 The parameter values of schemes 2 and 3

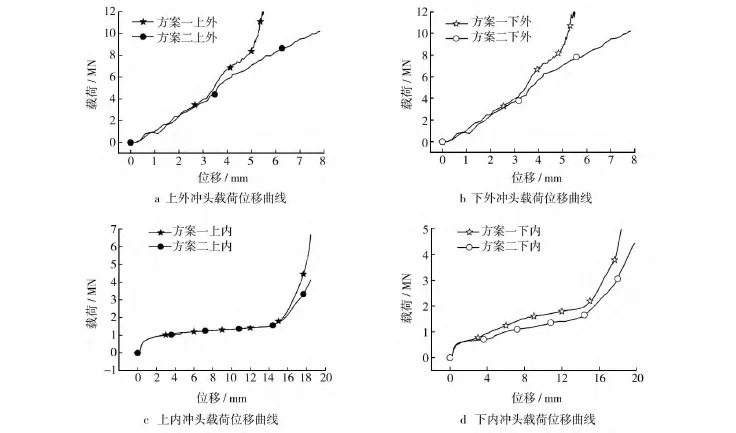
圖6 方案二三各沖頭載荷位移曲線Fig.6 The load-displacement curves of different punches in schemes 2 and 3

4 方案二數值分析

4.1 方案二模擬結果

如圖7所示，從速度矢量場可以分析金屬流動的情況。圖7a隨著上中沖頭向下擠壓，上中沖頭兩側相當于反擠過程，兩側金屬流向和上中沖頭運動方向相反。上中沖頭擠壓過程中齒形中間部位接觸到凹模，齒形兩端向外流動。擠壓過程中鍛件克服屈服強度產生塑性變形，90%以上塑性功轉化為熱能［6］和摩擦生熱，使鍛件表面溫度達250℃左右，如圖8a可以看到中間輪轂處溫度分布。方案二第Ⅰ階段變形較大使得鍛件等效應力范圍較大，如圖9a。

忽略了方案二第Ⅱ階段速度矢量分布、溫度分布和等效應力分布，由于第Ⅱ階段是單純下內沖頭上頂過程，力比較小，對速度、溫度和等效應力分布產生的影響可忽略。

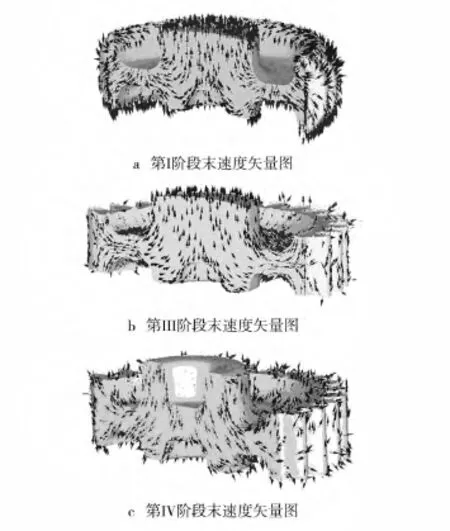
圖7 方案二各階段速度矢量圖Fig.7 The velocity vector diagram of different stages for scheme 2

第Ⅲ階段上下外沖頭對擠成形出齒形。如圖7b所示，從速度矢量場可以看出齒形兩端向中間流動，雙向墩擠有利于減小成形載荷，并且凹模可以產生有利摩擦使得齒輪角隅比較容易充滿（雙向墩擠與浮動凹模類似，均可以產生有利摩擦），從圖8b可以看出齒輪表面溫度在170℃左右，兩端角隅由于產生毛刺，溫度達到300℃左右。擠壓過程中隨著溫度的變化，材料應力應變曲線也會變化，發生材料軟化現象，能夠降低載荷。從圖9b可以看出擠壓齒形部分時，輪轂部分達到屈服強度產生塑性變形，使得輪轂分流腔產生分流減壓降低齒輪成形載荷。從圖10中可以看到，第Ⅲ階段擠壓到191步齒形填充比較理想，此時上下外沖頭載荷為10.2 MN。

第Ⅳ階段為上內沖頭向下擠壓形成凸臺凹槽，如圖7c所示，凸臺處金屬向下和沿徑向流動使得凸臺平整均勻。從圖8c和圖9c可知，分流面表面溫度在250℃左右且仍然產生塑性變形，可知輪轂分流腔還起著分流減壓作用。

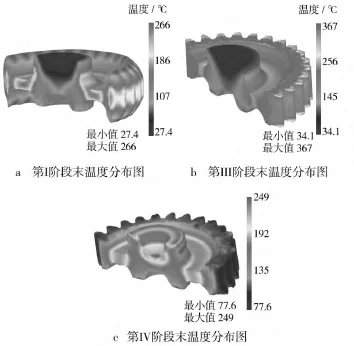
圖8 方案二:各階段溫度分布（℃）Fig.8 The temperature distribution of different stages

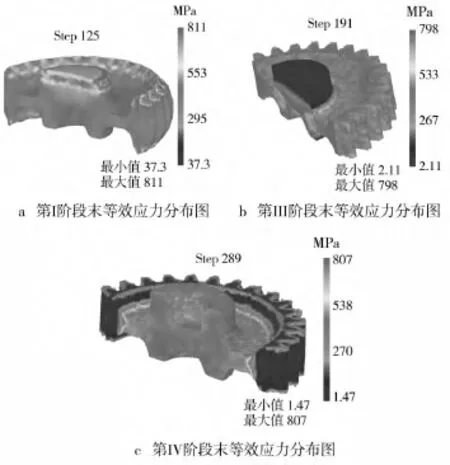
圖9 各階段等效應力分布Fig.9 The equivalent strain distribution of different stages

圖10 齒形填充圖Fig.10 The tooth filling diagram

4.2 模具應力分析

將圖4b各個沖頭峰值載荷除以沖頭橫截面積，可以獲得各個沖頭最大單位壓應力。各個沖頭最大平均壓應力能夠宏觀反應沖頭受力情況，如表3所示上下外沖頭的最大平均壓應力為1912 MPa。Deform-3D軟件能夠將坯料受到的載荷準確反向加載到模具沖頭上，可以計算出各個沖頭應力分布情況。以上外沖頭為例，表3中上外沖頭最大應力為2450 MPa，此應力為沖頭應力集中點或者網格畸變點，從圖11沖頭應力分布圖中觀察，上外沖頭應力最大分布在2150 MPa左右。一般冷擠壓模具許用單位壓力在2500 MPa左右。經過計算其他沖頭應力分布，模具滿足條件。證明方案二的工藝具有參考指導意義。

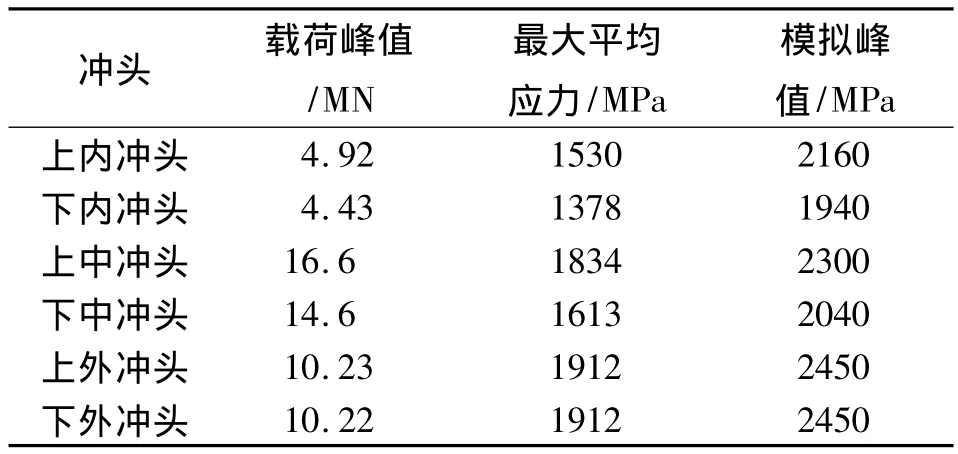
表3 方案二各沖頭應力分Table 3 The stress analysis of different punches in scheme 2

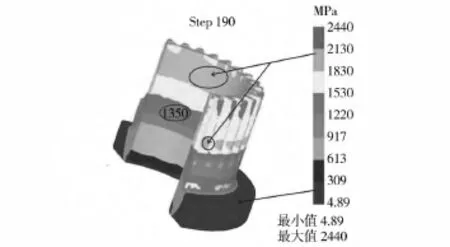
圖11 上外沖頭應力分布Fig.11 Stress distribution of the top out die

5 結論

通過Deform-3D軟件模擬大直徑大模數帶轂直齒輪3種成形工藝，通過對比分析優化成形方案，分析了工藝方案原理，對鍛件溫度場、速度矢量場、等效應力場以及模具受力情況進行了分析。根據帶轂直齒輪的特點，巧妙地將分流面設計在輪轂處來起到分流加壓目的，經過分析得出以下結論。

1）在有輪轂分流腔時，鍛件上內凸臺處有無接觸對齒形成形載荷的影響可忽略。

2）輪轂中分流腔對載荷影響很大，方案二能大幅度減小載荷。

3）采用方案一和方案二對齒輪成形比較有利，齒形金屬填充飽滿，齒形模具應力在許用范圍內，新工藝可為生產實踐提供指導。

［1］江雄心，林治平.帶轂直齒圓柱齒輪精鍛成形的上限分析［J］.塑性工程學報，1998，5（1）:8—14.

JIANG Xiong-xin，LIN Zhi-ping.The Upper Bound A-nalysis of the Precision Forging Process for Spur Gear with Boss［J］.Journal of Plasticity Engineering，1998，5（1）:8—14.

［2］胡成亮，施衛兵，徐祥龍，等.帶轂直齒輪冷精鍛新工藝及其數值模擬［J］.上海交通大學學報，2009，43（9）:1494—1497.

HU Cheng-liang，SHI Wei-bing，XU Xiang-long，et al.A Novel Cold Precision Forging Process of Spur Gear with Boss and Its Numerical Simulation［J］.Journal of Shanghai Jiaotong University.2009，43（9）:1494—1497.

［3］寇淑清，楊慎華，付沛福，等.高精度直齒圓柱齒輪冷鍛成形加工方法的研究［J］.鍛壓技術，2000，25（5）:10—12.

KOU Shu-qing，YANG Shen-hua，FU Pei-fu，et al.Research on Cold Forging Methods of Accurate Spur Gears［J］.Forging ＆ Stamping Technology，2000，25（5）:10—12.

［4］KONDO K，OHGA K.Precision Cold Die Forging of a Ring Gear by Divided Flow Method［J］.International Journal of Machine Tools and Manufacture，1995，35（8）:1105—1113.

［5］MAMALIS A G，MANOLAKO S D E，BALDOUKAS A K.Simulation of the Precision Forging of Bevel Gears Using Implicit and Explicit FE Techniques［J］.Journal of Materials Processing Technology，1996，57（1-2）:164—171.

［6］CHITKARA N R，KIM Y J.Near-net Shape Forging of Crown Gear:Some Experimental Results and an Analysis［J］.International Journal of Machine Tools＆ Manufacture，2001，41（3）:325—346.

［7］SONG J H，IM Y T.Process Design for Closed-die Forging of Bevel Gear by Finite Element Analyses［J］.Journal of Materials Processing Technology，2007，192-193（1）:1—7.

［8］Kondo K.Developments of New Precision Cold Die Forging Processes［C］//Advanced Technology of Plasticity，Proc.1st.ICTP，Tokyo，1984.

［9］程羽，楊程，臧順來，等.齒輪精密成形技術的研究［J］.塑性工程學報，2004，11（6）:62—68.

CHENG Yu，YANG Cheng，ZANG Shun-lai，et al.A Study on Precision Forging of Spur Gear［J］.Journal of Plasticity Engineering，2004，11（6）:62—68.

［10］CHOI J C，CHOI Y.Precision Forging of Spur Gears with Inside Relief［J］.International Journal of Machine Tools and Manufacture，1999，39（10）:1575—1588.

［11］孫紅星，劉百宣，王偉欽，等.直齒圓柱齒輪雙向擠墩均勻成形工藝研究［J］.熱加工工藝，2013，42（17）:1—4.

SUN Hong-xing，LIU Bai-xuan，WANG Wei-qin，et al.Study on Two-way Extrusion-upsetting Uniform Forming Process of Spur Gears［J］.Hot Working Technology，2013，42（17）:1—4.

［12］劉華，席慶坡，霍艷軍，等.圓柱齒輪冷精鍛數值模擬及其輪齒修形規律［J］.西安交通大學學報，2004，38（11）:1186—1189.

LIU Hua，XI Qing-po，HUO Yan-jun，et al.Numerical Simulation to Mold Modification of Cold Precision Forging of Spur Gear［J］.Journal of Xi'an Jiaotong University，2004，38（11）:1186—1189.

［13］胡成亮，劉全坤，趙震，等.考慮彈性變形行為的齒形凹模修正方法［J］.上海交通大學學報，2009，43（1）:52—55.

HU Cheng-liang，LIU Quan-kun，ZHAO Zhen，et al.Modification Method of Gear-Shaped Die Considering E-lastic Deformation Behavior［J］.Journal of Shanghai Jiaotong University，2009，43（1）:52—55.

［14］CEILIK M.Comparison of Three Teeth and Whole Body Models in Spur Gear Analysis［J］.Mechanism and Machine Theory，1999（34）:1227—1235.

［15］李建國，湯文成.基于熱力耦合的減振軸套擠壓成形有限元模擬研究［J］.機械設計與制造，2009（10）:30—33.

LI Jian-guo，TANG Wen-cheng.Finite Element Simulation Research of Vibration bushings Forging Based on the Thermal-mechanical Coupling［J］.Machinery Design＆ Manufacture，2009（10）:30—33.