基于自抗擾技術的撓性航天器高精度指向控制

宋 斌，顏根廷，李 波，鄭鵬飛

（上海宇航系統工程研究所，上海 201109）

0 引言

作為在軌服務的關鍵技術之一，近距離時對空間目標的跟蹤和相對狀態的保持，是航天器實現在軌維護或維修等空間任務的前提，因此航天器對空間目標的高精度姿態指向控制作為一個重要而嶄新的課題，逐漸受到關注和重視［1－5］。文獻［1－2］研究了飛行器相對目標姿態指向跟蹤控制；文獻［3］針對航天器的單軸指向控制提出了兩段控制法以保證控制系統的大范圍漸近穩定；文獻［4］針對哈勃望遠鏡的高精度指向控制提出了五種應用改進方案，提升了系統的控制性能。但這些控制方案未考慮或不能有效抑制外干擾和系統參數不確定性及撓性振動。

自抗擾控制技術首先利用跟蹤微分器實現對系統輸入信號的快速無超調跟蹤，其次將系統自身模型的不確定性作為系統的內擾，與系統的外擾視作整個系統的總擾動，通過擴張觀測器對系統的狀態和總擾動進行估計，最后利用非線性狀態誤差反饋控制律獲得擾動分量的補償控制［6］。自抗擾控制方法實質上有很強的魯棒控制作用，既補償了系統內部參數及模型的擾動，又抑制了外擾，且無需精確的系統模型，因此在航天領域獲得了廣泛應用［5、7－9］。為同時解決用戶衛星天線控制系統的魯棒性、解耦控制和高精度跟蹤控制，文獻［5］采用非線性自抗擾控制方法提出了一類新型天線跟蹤指向控制方案；文獻［7－8］針對航天器的快速機動，設計了基于自抗擾技術的控制律，但沒有考慮模型的不確定性和執行機構奇異避免問題。此外，傳統自抗擾控制器設計中常采用非光滑fal（e，ε，δ）函數設計擴張觀測器，易產生高頻抖振，不利于工程應用。文獻［9］通過構造秦函數實現了連續擴張觀測器的設計，有效避免了擴張觀測器在應用過程中的抖振。單框架控制力矩陀螺（SGCMG）作為航天控制領域常用的執行機構，通過轉動其高速旋轉的轉子與本體進行角動量交換實現姿態控制，雖具可靠性高、響應快、力矩大、功耗低等優點，但存在的奇異問題導致其難以用于操縱律研究和應用。文獻［10－11］分析了SGCMGs奇異面的可視化，以金字塔構型為例給出了所有奇異框架角的解析表達式，并提出了一系列有效的奇異避免操縱律。

本文針對無姿態角速度反饋的航天器的目標高精度姿態指向控制，對一類新穎的基于自抗擾技術的控制方案進行了研究。

1 數學模型

1.1 相對指向姿態定義

設視線測量跟瞄設備安裝于航天器本體，跟瞄設備測量坐標系Ob－XsYsZs如圖1所示。圖中：Ob－XbYbZb為本體坐標系；ρ為目標相對航天器的視線距；α為視線在星載跟瞄設備測量坐標系中的高低角，定義為視線與其在XsObYs平面的投影間的夾角；β為視線在測量坐標系中的方位角，定義為視線在XsObYs平面的投影與ObXs軸的夾角。

根據以上定義，可得跟瞄設備的測量模型為

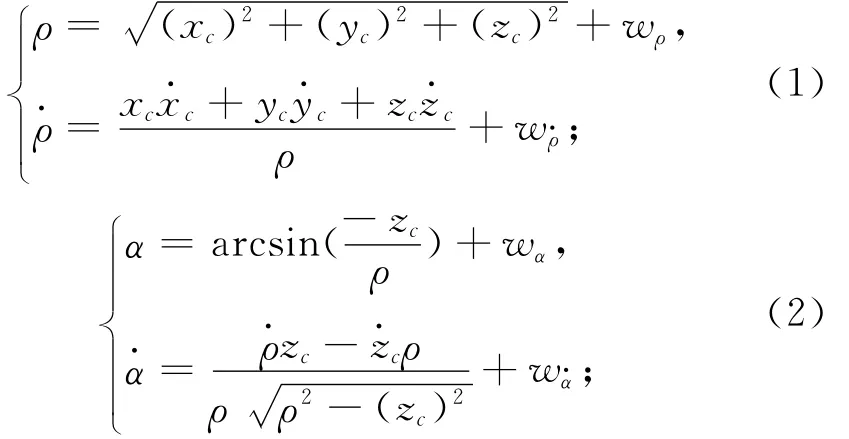
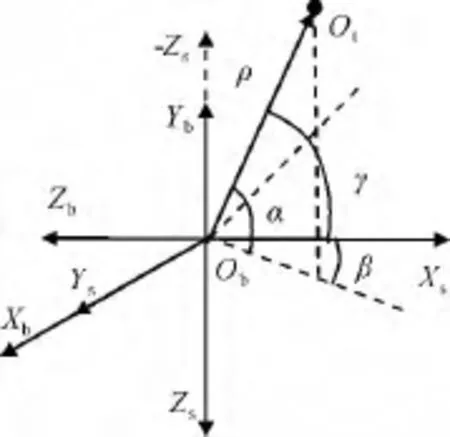
圖1 相對姿態指向坐標系Fig.1 Relative attitude pointing coordinate

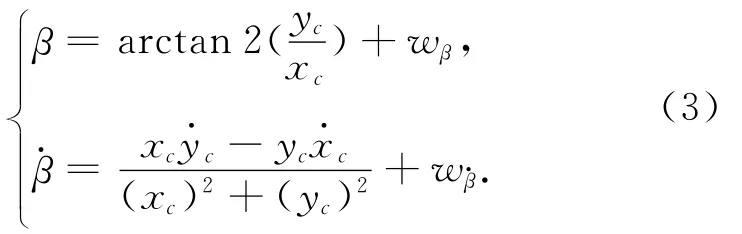
當航天器天線沿飛行器本體 －ObZb軸安裝，且航天器天線無驅動能力時，控制目標需要航天器本體軸－ObZb高精度指向目標。由此，可得航天器本體坐標系與跟瞄坐標系的關系為

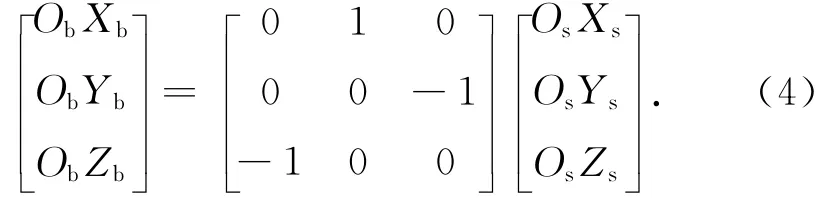
為保證視線軸與－ObZb軸重合，可通過繞本體軸1－2－3依次旋轉－α，β，ψω實現。則姿態矩陣為

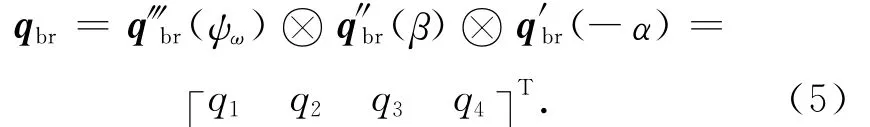
式中：q1＝cos（0.5ψω）cos（0.5β）cos（0.5α）－sin（0.5ψω）sin（0.5β）sin（0.5α）；q2＝ －sin（0.5×ψω）sin（0.5β）cos（0.5α）－cos（0.5ψω）cos（0.5β）×sin（0.5α）；q3＝cos（0.5ψω）sin（0.5β）cos（0.5α）－sin（0.5ψω）cos（0.5β）sin（0.5α）；q4＝sin（0.5ψω）×cos（0.5β）cos（0.5α）＋cos（0.5ψω）sin（0.5β）×sin（0.5α）。此處：ψω為繞偏航軸的轉動，可控制航天器保持偏航軸慣性空間定向。

此外，由圖1可得視線角γ及其速率分別為

1.2 撓性航天器相對指向動力學

考慮執行機構為SGCMGs，帶撓性天線和南北太陽帆板的航天器動力學方程和振動方程為

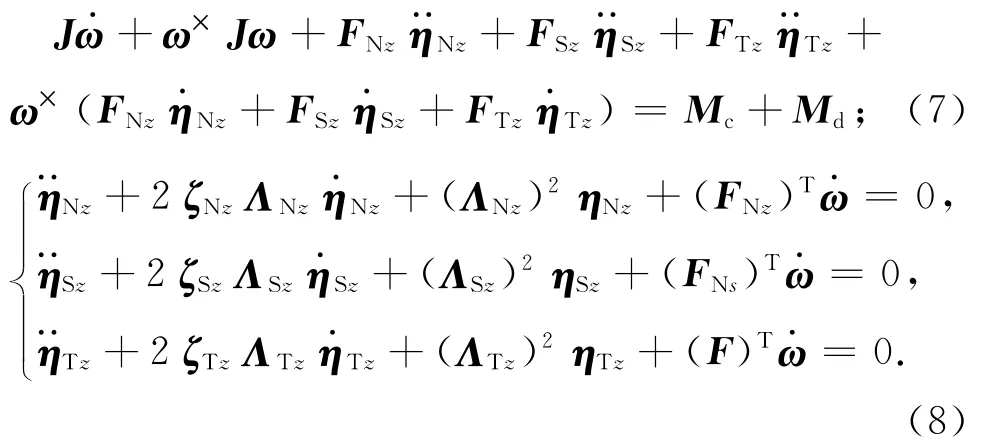
式中：J為航天器的轉動慣量陣，且J＝J0＋ΔJ；ω為系統相對慣性空間的姿態角速度；符號“×”表示斜對稱陣；FNz，FSz，FTz分別為北帆板、南帆板和天線的振動運動與承載平臺平移運動的耦合系數，且FNz＝［FNzXFNzYFNzZ］T，FSz＝［FSzXFSzYFNzZ］T，FTz＝［FTzXFTzYFTzZ］T；ηNz，ηSz，ηTz為撓性模態坐標；ξNz，ξSz，ξTz為撓性模態阻尼系數；ΛNz，ΛSz，ΛTz為撓性模態振型頻率；Mc為執行機構提供的系統控制力矩，且Mc＝［McxMcyMcz］T；Md為系統干擾力矩，且Md＝［MdxMdyMfz］T。此處：J0為轉動慣量的標稱值；ΔJ為轉動慣量的不確定項。

為便于控制器設計，將航天器動力學方程表示為

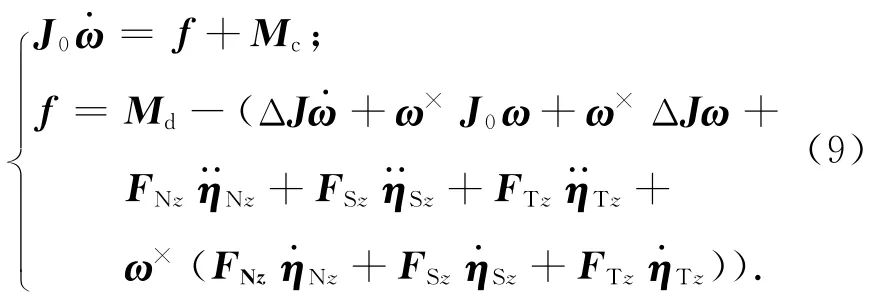
1.3 系統模型簡化

目標高精度指向控制期間，設航天器控制系統無角速度反饋，當姿態為小角度，且采用SGCMGs作為執行機構的控制力矩遠大于干擾力矩時，則可選取主慣量軸作為飛行器體坐標系，即具有主對角優勢，可不考慮各軸間的耦合。令J＝diag［JxJyJz］，J0＝diag［JxxJyyJzz］，ΔJ＝diag［ΔJxxΔJyyΔJzz］，則航天器姿態動力學方程可簡化為

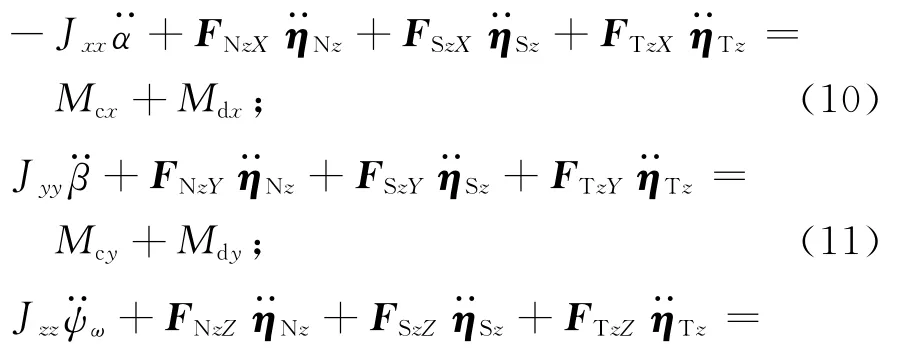
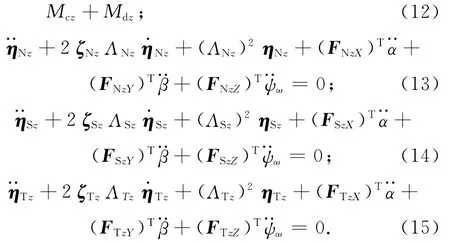
由此可得航天器動力學的簡化模型

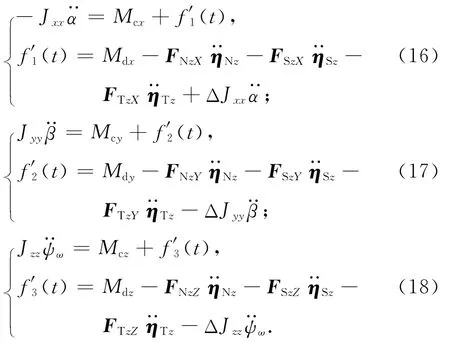
式中：f′i（t）為系統的總不確定項，包含干擾力矩、太陽帆板和天線的撓性振動對航天器的動力學耦合。此處：i＝1，2，3。定義

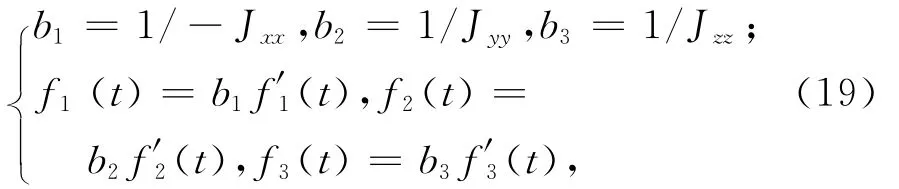
則簡化模型可改寫為

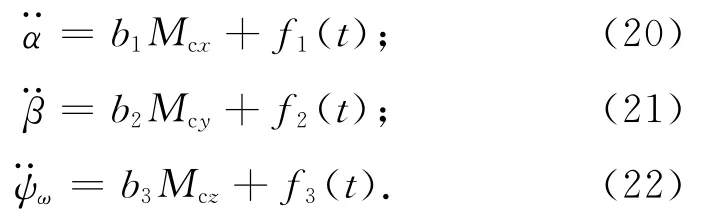
2 無角速度反饋的自抗擾控制器設計

2.1 秦函數定義

擴張觀測器（ESO）是自抗擾控制技術的核心，不僅能觀測出系統的狀態，而且可對系統的不確定性和外部干擾的總和進行實時觀測，并利用觀測值實現動態補償線性化和擾動抑制。傳統ESO設計中，使用的函數和han（e，ε）＝｜e｜εsigne易導致高頻抖振，因此通常將其改造成在原點處具有線性段的連續冪次函數

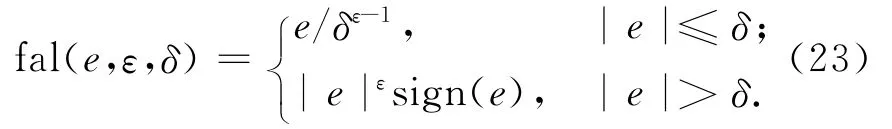
式中：e為觀測誤差；δ為定義的線性段的區間長度，δ越大，濾波效果越好，但會增加跟蹤的延遲，一般可選取為采樣時間的5～10倍；ε∈（0，1），ε越小，跟蹤就越快，但濾波效果會變差。因han（e，ε）函數在原點處的導數無窮大而會導致高頻抖振，將其改進為fal（e，ε，δ）后，雖連續但不可導。若誤差在其線性段內變動，則可有效抑制高頻抖振，但δ的取值對系統性能的影響較大，當其誤差變動到線性段外，仍會導致抖振甚至振蕩更大。因此，需對fal（e，ε，δ）繼續進行修正，將其構造成光滑連續的函數是解決此問題的關鍵［9］。

當｜e｜≤δ時，為滿足函數在零點連續光滑且取值為零，定義

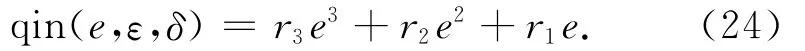
若式（24）滿足連續光滑條件，即當e＝δ時qin（）＝δε；當e＝－δ時qin（）＝－δε；當e＝±δ時qin（）＝εδε－1；當e＝0時qin（）＝δε－1。根據上述條件，可得

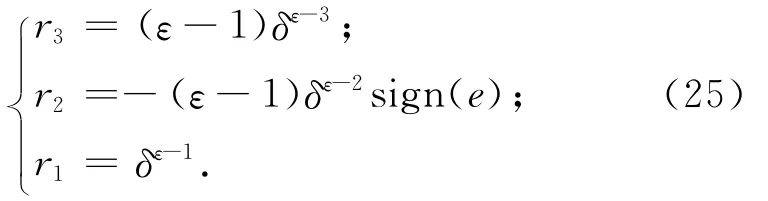
由此，改進的qin（e，ε，δ）可定義為

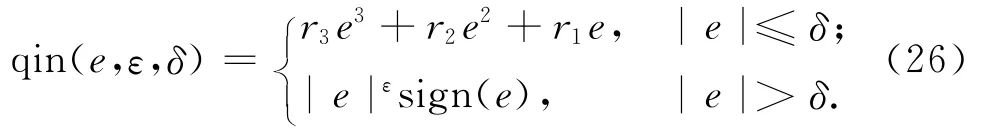
取ε＝0.5，δ＝0.4，可得上述三種函數han（e，ε），fal（e，ε，δ），qin（e，ε，δ）針對輸入誤差的輸出如圖2所示。由圖可知：qin（e，ε，δ）函數光滑且連續，可避免擴張觀測器的高頻抖振。

2.2 無角速度反饋的自抗擾控制器設計

針對簡化系統式（20）～（22），分別對三個通道進行自抗擾控制器設計，其控制系統如圖3所示。因控制系統無角速度反饋，三個通道均為二階系統，因此構造的擴張觀測器應為三階。

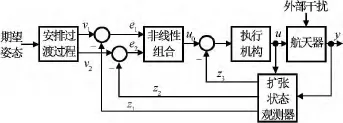
圖3 撓性航天器對目標高精度指向自抗擾控制Fig.3 ADRC system for flexible spacecraft high－accuracy attitude pointing

對式（20）的高低回路的簡化動力學模型，定義x1＝α，x2＝，可得二階非線性級聯系統

為增強系統對參數攝動和擾動的魯棒性，以及快速精確的跟蹤航天器輸出，設計中采用了微分跟蹤器安排過渡過程

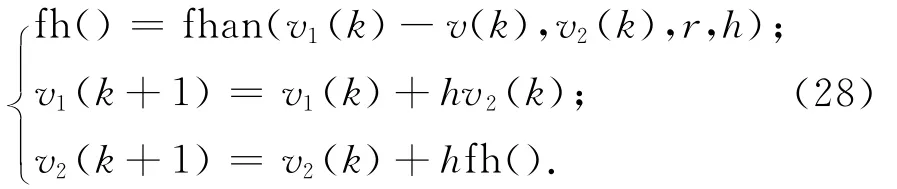
式中：

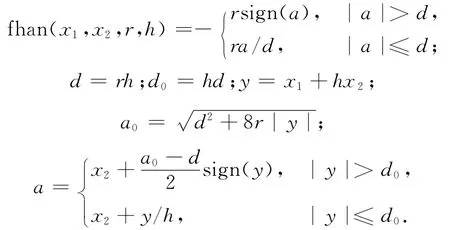
此處：r為速度因子，其大小決定跟蹤速度的快慢，其選取取決于受控對象的承受能力和可提供的控制能力；h為系統的微積分步長。

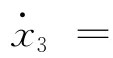
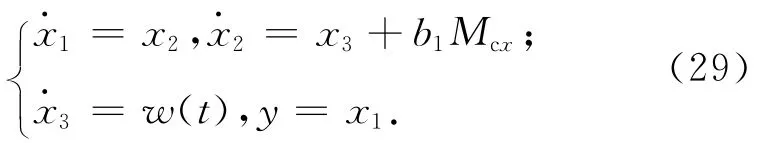
繼而設計擴張狀態觀測器對系統的狀態及擴張狀態（對f1（t）進行實時估計）

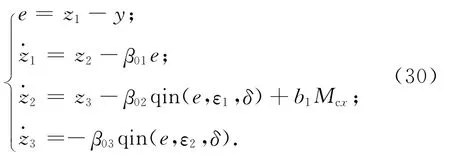
則只需選擇適當的參數β01，β02，β03，該三階ESO能較好地估計系統式（29）的狀態變量x1（t），x2（t）以及被擴張的狀態的實時作用量x3（t），有z1（t）→x1（t），z2（t）→x2（t），z3（t）→x3（t）。再利用f1（t）估值z3（t）對航天器動力學系統進行擾動動態補償線性化，設計控制律

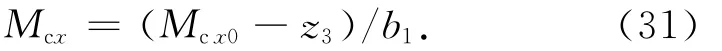
由此，式（27）表示的高低回路動力學模型解耦成一個串聯積分系統

雖然擴張觀測器對系統的總擾動有很好的估計能力，但在動態反饋補償后不可避免存在補償殘差，因此需對上述串聯積分系統進一步設計非線性狀態誤差反饋控制律

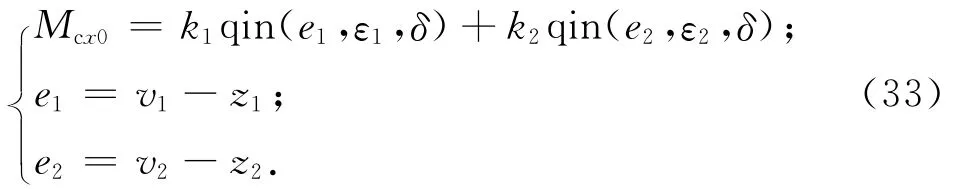
至此，高低回路的自抗擾控制律設計完成。實際工程應用中，控制算法常采用離散計算，因此需對上述自抗擾控制律進行離散化，有

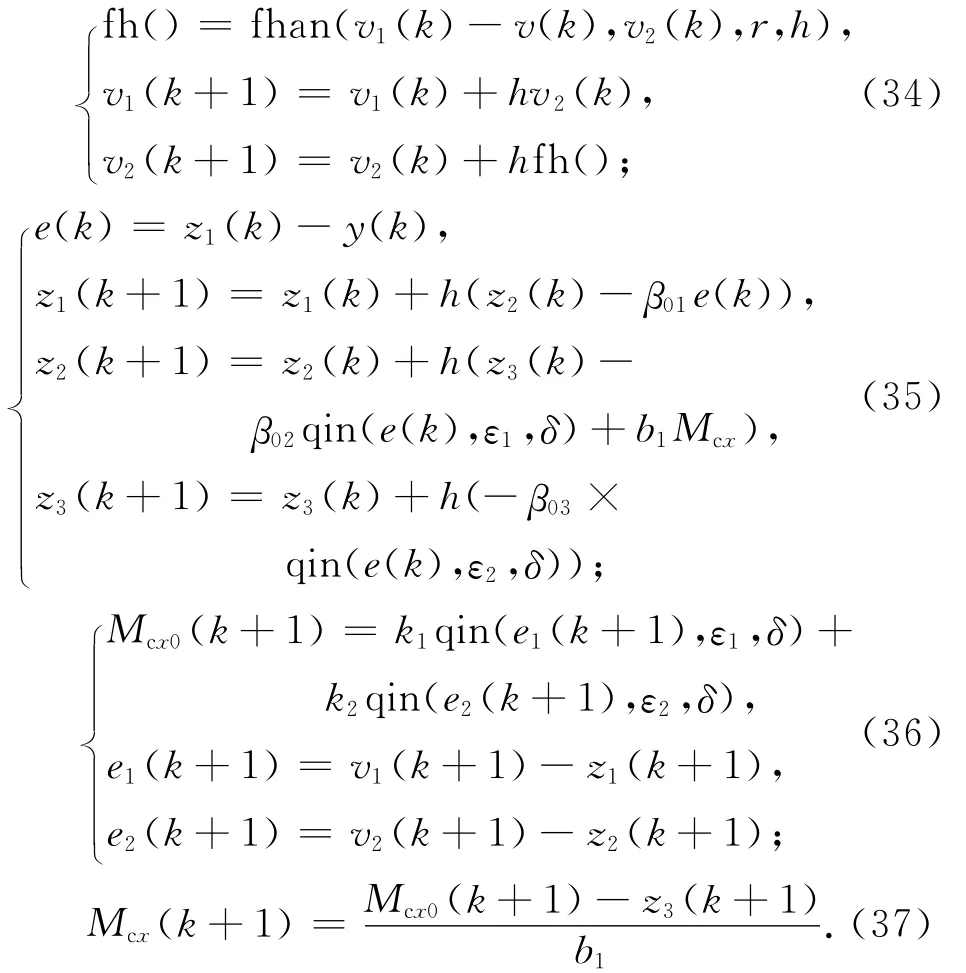
根據上述的自抗擾控制器的設計原理，可分別對目標相對航天器的視線回路和航天器本體的偏航回路單獨進行設計。

3 執行機構操縱律設計

在目前的各種SGCMGs構型中，五棱錐構型的性能最優。在正常工作和僅有1個力矩陀螺失效時，五棱錐構型的包絡效益均為最大，且包絡效益損失最小，同時其顯奇異點分布靠近包絡面且損失率較小，可在一個較大的動量體內進行動量控制。因此，對一長期在軌服務運行的撓性航天器，五棱錐構型是一個很好的選擇。針對五棱錐構型的控制力矩陀螺群，其提供的控制力矩

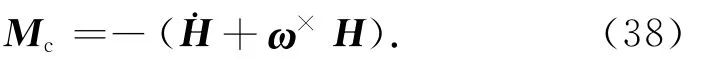
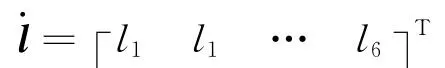
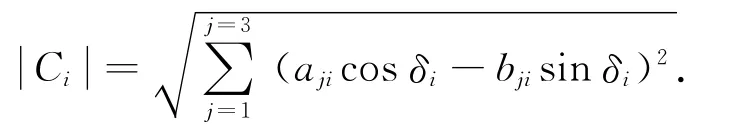
針對前文設計的對目標高精度指向的自抗擾控制律Mc，可得SGCMGs的或力矩指令為

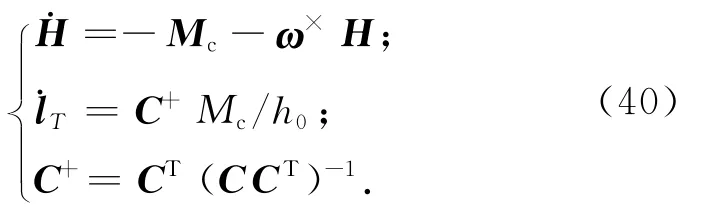
此即為常用的偽逆操縱律，顯然當行列式det（CCT）＝0時式（40）無解，即陀螺群框架處于奇異狀態。框架奇異并不表明一概無力矩輸出，而是沿奇異方向無力矩輸出。當C的行不滿秩或秩小于3，框架構型奇異，因而陀螺群框架構型的量度可為D＝det（CCT），D值越大，表明力矩陣C的特征值越大，框架構形離奇異狀態越遠，產生沿任一方向的陀螺力矩的可能性越大。

當SGCMGs構形奇異時，不能用式（40）計算框架角速度指令。在航天器的控制過程中，可利用框架構形的D實時評估構形品質，并作為限制條件，不斷將框架再構形，預防進入奇異狀態。由于框架再構形不應引起附加的陀螺力矩，這種框架構形的調整可稱為空轉，再構形指向稱為空轉指令或空轉控制［12］。因此框架角速度指令為

式中：為空轉指令，滿足零空間定義C＝0；aN為待定標量系數，與再構形的反應快慢有關，需從控制系統總體需求考慮；E為單位矩陣；

此處：em，k為量度矩陣CCT的元素；符號“′”表示元素em，k對li的偏導數，即為矩陣?（CCT）／?li的元素。

因CCT為3×3對稱矩陣，em，k＝ek，m，e′m，k，i＝e′k，m，i，則式（42）可化為

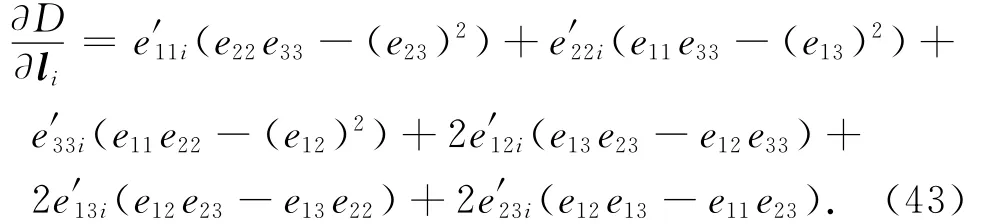
至此，SGCMGs的操縱律設計完成，通過引入零空間空轉指令避免奇異，以達到有效的控制效果。

4 仿真

為驗證本文設計的無角速度反饋的自抗擾控制器和控制力矩陀螺群奇異避免操縱律的有效性，對存在外部干擾和模型不確定性的撓性航天器高精度指向控制進行了Matlab／Simulink數值仿真驗證。仿真中主要的模型和控制參數分別為：航天器模型，J0＝diag［6 282 5 712 7 362］kg·m2，ΔJ＝diag［612 －438 518］kg·m2，初始姿態角α＝－10.0°，β＝8.0°，ψω＝6.0°，初 始 角 速 度ω0＝［0.3 －0.3 0.3］（°）／s，姿 態 測 量 精 度 （3σ）0.03°；控制器，β01＝1.8，β02＝1.2，β03＝0.26，ε1＝0.5，ε2＝0.25，δ＝0.4，k1＝0.01，k2＝0.048，h0＝25N·m·s，aN＝0.2。此外考慮系統的干擾力矩，包括軌道控制的干擾力矩、空間環境干擾力矩、活動部件運動干擾力矩等。

為進行驗證，比較了本文設計的自抗擾控制方案與傳統PD控制方案。目標星在航天器星載跟瞄設備測量坐標系中相對姿態角的時間響應仿真結果分別如圖4、5所示。由圖可知：自抗擾控制器能快速完成高精度指向控制，60s可達到穩定精度0.05°；傳統PD控制在100s時的穩定精度仍大于0.1°，控制效果遠不如自抗擾控方案。

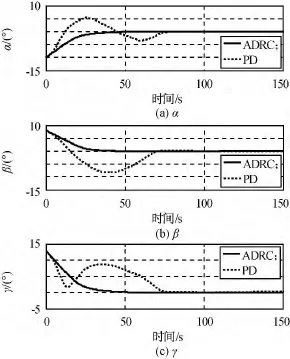
圖4 相對姿態角時間響應Fig.4 Time response of relative attitude angle

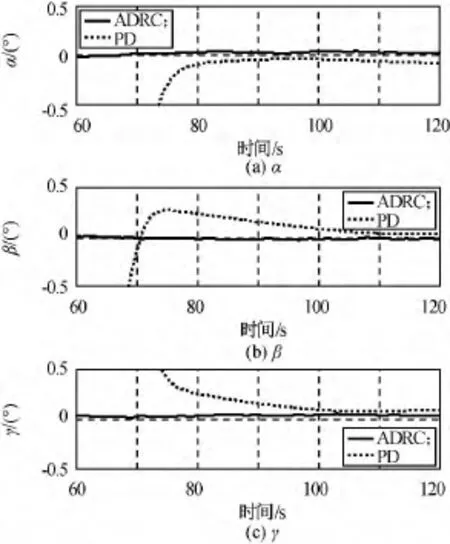
圖5 相對姿態角時間響應局部放大Fig.5 Partial amplified view of relative attitude angle

相對姿態角速度仿真如圖6所示。由圖可知：自抗擾控制方案中姿態角速度在60s時達到的穩定度為0.02（°）／s，PD控制則需要80s。由于自抗擾控制器中安排過渡過程模塊的作用，系統狀態（相對姿態角及其角速度）可快速且無超調地達到穩態，控制性能明顯優于PD控制方案。單SGCMGs的三軸輸出角動量和控制力矩的時間響應仿真結果分別如圖7、8所示。由圖可知：PD控制方案中執行機構輸出的角動量和控制力矩明顯大于本文設計方案，浪費了系統資源。

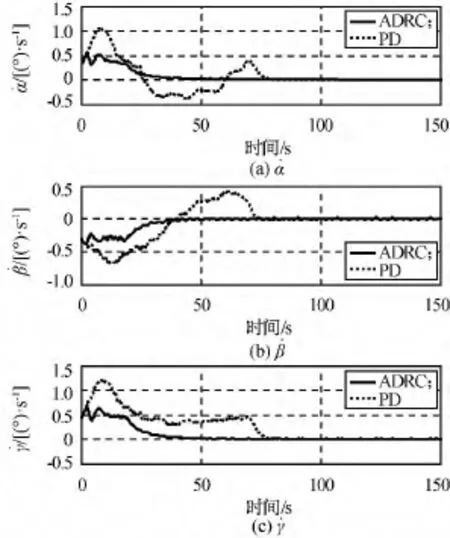
圖6 相對姿態角速度時間響應Fig.6 Time response of relative attitude angle velocity

為避免單SGCMGs出現奇異而無法輸出期望控制力矩，本文設計了奇異避免操縱律，其奇異量度值的時間響應如圖9所示。由圖可知：D會在接近0時逐漸逃離0點，驗證了奇異避免操縱律的有效性。此外，針對不同的工況和不同控制參數進行仿真對比，結果顯示本文設計的自抗擾控制方案總體控制性能和效果明顯優于傳統PD控制方案。其中，安排過渡過程能緩解經典PD控制中系統超調與快速性間的矛盾，使系統狀態能快速無超調地達到高精度穩定；擴張狀態觀測器利用擴展的狀態對不確定性和外部擾動的實時作用進行觀測，并利用其實現動態補償線性化及擾動抑制。可見，自抗擾控制器不依賴于被控對象的精確數學模型，抗干擾能力強，控制效果好，可用于多種非線性系統設計。

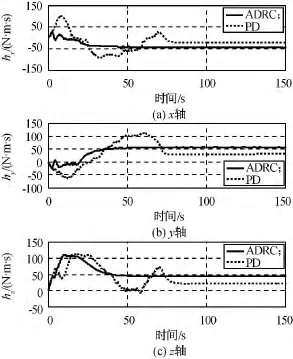
圖7 控制力矩陀螺群輸出三軸角動量Fig.7 Time response of three axial angle moment of SGCMGs

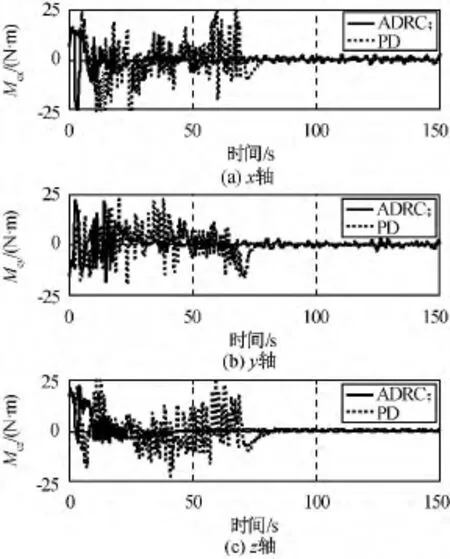
圖8 控制力矩陀螺群輸出三軸控制力矩Fig.8 Time response of three axial control torque of SGCMGs

5 結論

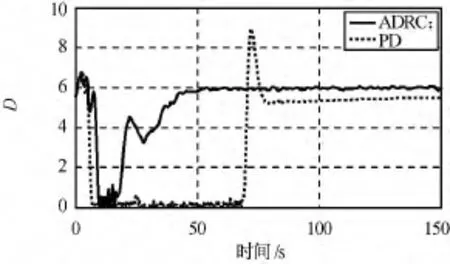
圖9 控制力矩陀螺群奇異量度Fig.9 Measurement values of singularitie of SGCMGs

本文針對航天器對目標高精度姿態指向控制問題，提出了一類新穎的基于自抗擾技術的控制方案和基于SGCMGs的奇異避免操縱律。對非合作目標相對姿態控制系統進行建模，考慮航天器轉動慣量偏差、外部干擾和撓性附件振動，引入一光滑連續的秦函數，構造三階擴張觀測器，對系統姿態角速度和總擾動進行觀測，并利用其實現動態補償線性化及擾動抑制。針對SGCMGs作為執行機構常存在的奇異，通過引入零空間空轉指令設計了一類奇異避免操縱律。將提出的控制系統方案與傳統PD控制用于某撓性航天器模型，仿真結果驗證了本文方案的有效性、合理性和優越性。可見，雖然自抗擾控制方案也存在結構復雜、計算量大、參數調試繁瑣等缺點，但其不依賴于被控對象的精確數學模型，抗干擾能力強，控制效果好，可用于多種非線性系統設計和大撓性航天器姿態控制。

［1］ 張志國，李俊峰，賀音寶西.衛星編隊飛行指向跟蹤姿態控制［J］.清華大學學報，2006，46（11）：1914－1917.

［2］ 王冬霞，石 恒，賈英宏，等.航天器姿態指向跟蹤的一種自適應滑模控制方法［J］.空間控制技術與應用，2010，36（6）：22－26.

［3］ 張洪華，王 芳.欠驅動撓性航天器的姿態指向控制［J］.宇航學報，2011，32（7）：1491－1501.

［4］ BUKLEY A P.Hubble space telescope pointing control system design improvement study results［J］.Journal of Guidance，Control，and Dynamics，1995，18（2）：194－199.

［5］ 朱承元，楊 滌，李順利.用戶衛星天線跟蹤指向自抗擾控制方法［J］.北京理工大學學報，2006，26（1）：82－86.

［6］ 韓京清.自抗擾控制器及其應用［J］.控制與決策，1998，13（1）：19－23.

［7］ 張樹瑜，郭文彥，耿 森，等.基于ADRC的撓性多體航天器快速姿態機動研究與應用［J］.上海航天，2010，27（6）：20－22.

［8］ 周黎妮，唐金國，李海陽.航天器姿態機動的自抗擾控制器設計［J］.系統工程與電子學報，2007，29（12）：2122－2126.

［9］ 齊乃明，秦昌茂，宋志國.高超速飛行器改進的自抗擾串級解耦控制器設計［J］.哈爾濱工業大學學報，2011，43（11）：34－38.

［10］ WIE B.Singularity analysis and visualization of single－gimbal control moment gyro systems［J］.Journal of Guidance，Control，and Dynamics，2004，27（2）：271－282.

［11］ WIE B.Singularity escape avoidance steering logic for control moment gyro systems［J］.Journal of Guidance，Control，and Dynamics，2005，28（5）：948－956.

［12］ 章仁為.衛星軌道姿態動力學與控制［M］.北京：北京航空航天大學出版社，1998：278－292.