試飛階段可靠性評估方法及試驗方案設計

高雅娟，陸 山

（1.中國飛行試驗研究院，西安710089；2.西北工業大學動力與能源學院，西安710072）

試飛階段可靠性評估方法及試驗方案設計

高雅娟1，陸 山2

（1.中國飛行試驗研究院，西安710089；2.西北工業大學動力與能源學院，西安710072）

提出將基于2參數威布爾分布的小子樣零故障壽命試驗方法用于航空發動機等高可靠性航空武器裝備設計定型試飛階段平均故障間隔時間評估以及可靠性專項試飛/地面試驗設計，通過計算給出可靠性評估及試驗設計系數用表；同時采用Matlab對航空發動機歷史試驗數據進行擬合，得到對應的形狀參數；在此基礎上，以某航空發動機為例對該方法工程應用的適用性和有效性進行驗證。結果表明：該方法具有較強的工程應用性，可用于解決試飛階段航空發動機等高可靠性產品可靠性評估及試驗設計問題。

可靠性評估；航空發動機；小子樣零故障壽命試驗方法；威布爾分布；航空武器裝備

0 引言

隨著航空武器裝備技術水平、可靠性研究與應用水平的提高，在設計定型/鑒定試飛或部隊試用階段，各方對可靠性評估工作越來越重視,將可靠性置于和性能同等重要的地位，對可靠性評估結論的準確性、評估方法的科學性、可靠性試驗設計的合理性均提出了更高要求。在實踐中，一方面由于高可靠性、長壽命產品研發和生產成本較高，其試驗鑒定難度較大，試驗周期和經費的矛盾也愈加突出。經典的試驗分析與評估方法如極大似然法[1]以及單側置信下限估計方法[2]受到了挑戰[3]；而概率權重法、相關系數優化法、矩估計法[4]和灰色估計法[5]等新的理論也因為在工程中實際試驗樣本量小而具有一定的局限性。另一方面，如何合理設計可靠性專項試飛及地面試驗，降低飛行試驗費用，縮短飛行周期，是未來可靠性評估驗證的發展趨勢。因此開展小樣本可靠性評估方法及試驗設計具有重要的理論意義及巨大的經濟價值，是當前以航空發動機為代表的高可靠性航空產品進行可靠性評估驗證時需要關注的問題。目前對航空發動機等高可靠性產品小樣本進行評估的方法主要有基于貝葉斯理論的小樣本可靠性評估方法[6]、基于威布爾分布的無故障數據可靠性評估方法[7-9]、基于改進型Bootstrap方法的小子樣試驗評估方法[10]等。但這些方法較為復雜，且偏理論，在工程中應用較困難。

本文提出將美國《航空渦噴渦扇渦軸渦槳發動機通用規范》[11]中給出的當壽命分布符合2參數威布爾分布時構件可靠壽命零故障試驗設計方法，推廣應用于試飛期間航空發動機等高可靠性航空裝備的可靠性評估及可靠性專項試驗設計中。

1 小子樣零故障壽命試驗方法

設產品失效服從2參數威布爾分布[11]

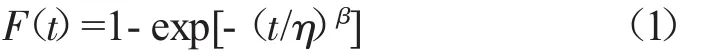
式中：F為2參數威布爾分布的分布函數；η為特征壽命；β為形狀參數；t為工作時間。

（t1，t2，L，tn）為 1 組隨機試驗件的故障時間樣本，將其按從小到大的順序排列，其最小次序統計量t(1)的分布函數可表示為

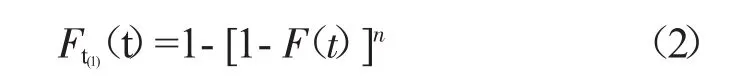
式中：Ft(1)

為t(1)的分布函數；n為試驗樣本數量。

將式（1）代入式（2）可得

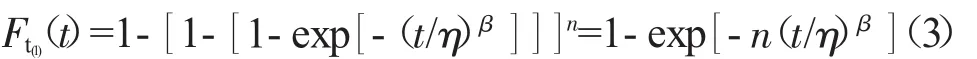
令tγ為威布爾分布的最小次序統計量累積分布函數的下側置信限，γ為相應的置信度，則最小次序統計量大于置信下限的風險為

由式（3）和式（4）得

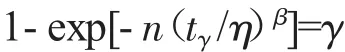
這樣，在已知形狀參數β置信度γ樣本數n和特征壽命η條件下，可得出每一試驗件所需的試驗時間。

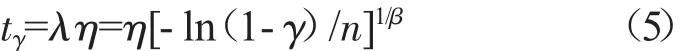
式中：λ為特征壽命乘子。

反之，已知形狀參數β、置信度γ和特征壽命乘子 λ=tγ/η，也可求出所需的試驗樣本數

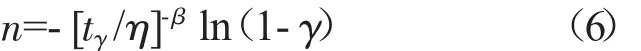
根據相關國軍標要求，試飛階段外場可靠性評估可取置信度γ=80%，此時的特征壽命乘子λ及樣本數n的系數見表1、2。

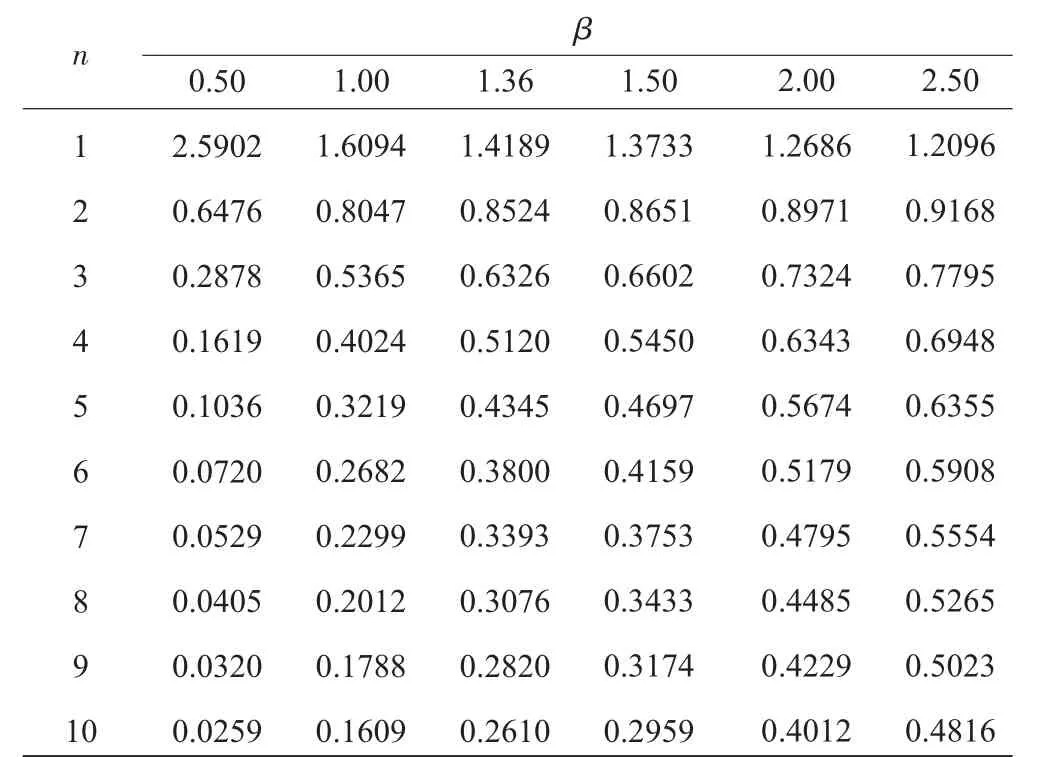
表1 零故障試驗方案特征壽命乘子λ（γ=80%）

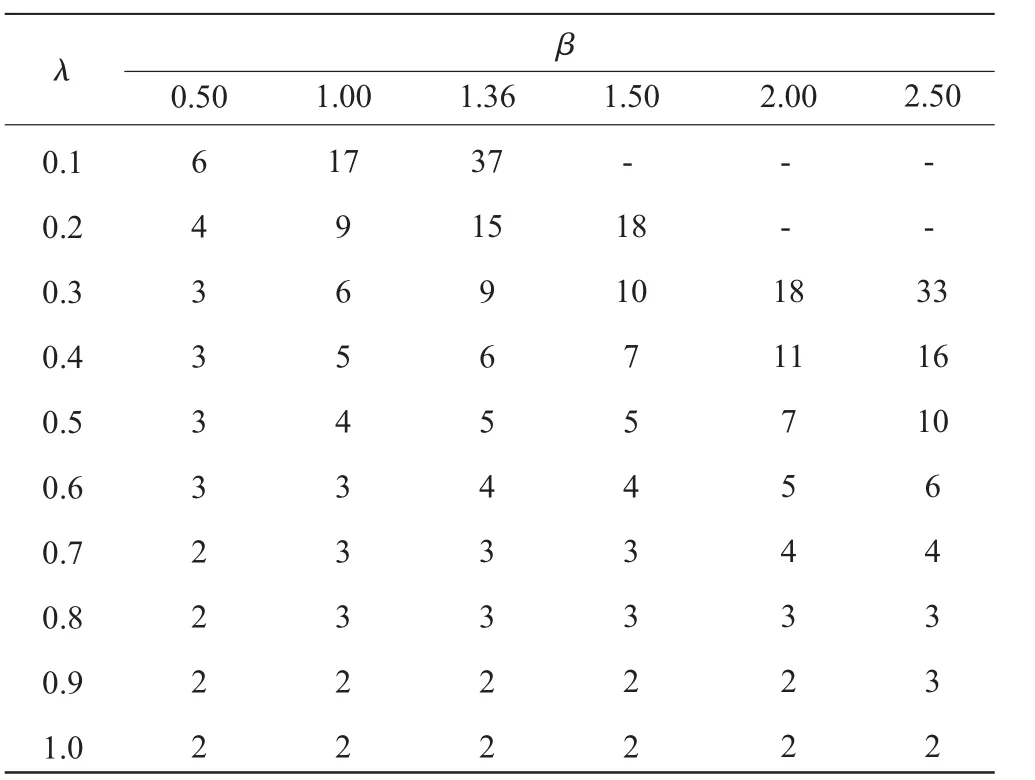
表2 零故障試驗方案所需試件數n（γ=80%）

2 零故障壽命評估方法在高可靠性產品評估中的應用

可靠性評估驗證工作是在綜合考慮生產方和使用方的利益以及試驗費用等諸多因素的基礎上制定科學合理的試驗方案，利用科學合理的數理統計學手段處理試驗數據，來驗證產品的可靠性指標是否滿足要求。隨著軍方對可靠性評估工作的重視，可靠性理念已貫穿于軍品的設計、生產、使用的各個階段，積累了大量的可靠性試驗數據，為航空裝備設計定型/鑒定試飛期間可靠性綜合評估提供了豐富的數據來源。在可靠性工程中，產品壽命分布類型可能是指數分布、正態分布、對數正態分布和威布爾分布等。由于威布爾分布含有3個參數，故其適應性較強，它可擬合浴盆曲線的3個階段，因而在可靠性工程技術中應用廣泛。

2.1 小子樣零故障產品可靠性評估方法

采用小子樣零故障試驗方法進行航空發動機等可靠性評估的步驟如下：

（1）采用威布爾分布對已有設計、研制階段的可靠性試驗數據或相似產品的歷史試飛數據進行擬合，確定各分布參數，從而確定該類產品壽命分布函數。由分布函數可得出任意給定可靠度時的壽命、給定壽命時的可靠度以及特征壽命值η；

（2）結合形狀參數β和參試產品數量n，查表1得到特征壽命乘子λ；

（3）根據式（5）計算得到當航空發動機或零部件可靠壽命達到某一規定值時所需的試驗時間t，與其試飛期間的實際工作時間T（可采用人工計時或在飛機或裝備上安裝相關的數據采集系統記錄）相比較，若t≤T，則證明其可靠性已達到規定要求。

2.2 可靠性專項試驗設計

隨著軍方對可靠性要求的提高，可靠性專項試飛或地面試驗已成為航空發動機及武器裝備設計定型/鑒定試飛的重要部分，能在真實的飛行環境條件下檢驗和評估產品的可靠性水平，為航空武器裝備的定型/鑒定提供重要依據和參考。

由上節可知，利用小子樣零故障壽命試驗方法，能確定給定壽命可靠度和試件數時某一置信度水平下所需的試驗時間，或給定壽命可靠度及試驗時間時所需的試件數。根據本文提出的方法，合理進行設計定型/鑒定試飛期間飛行試驗時間的設計，合理安排發動機數量以及試驗時間：

（1）在參試產品數量確定的情況下，結合科研試飛任務采集、記錄構件的工作時間，如果評估對象的工作時間不少于滿足某一給定概率壽命時所需的試驗時間，則產品的可靠性滿足要求；若不能達到所需的試驗時間要求，可根據理論計算結果，適當延長產品的試驗時間。這樣既可以避免試驗時間不夠，無法確定產品的可靠性是否滿足要求，又可以降低試飛成本；

（2）在產品試飛周期（即產品的工作時間）確定的情況下，可以根據該理論確定滿足某一概率壽命時所需的參試發動機數量，從而將壽命概率度量方法引入飛行試驗中的可靠性評估工作中，提高評估精度，為航空發動機及裝備的設計定型/鑒定提供可靠依據。

2.3 試飛階段失效分布類型分析

在試飛階段進行可靠性評估時，一般認為整機或電子類裝備的早期故障已被排除，進入偶發故障階段，因此采用基于指數分布的可靠性評估或試驗設計；航空發動機的機械構件的失效則服從2參數威布爾分布[12]。

為進一步確定航空武器裝備設計定型/鑒定試飛期間失效分布的類型，本文對航空電子設備以及航空發動機結構件的大量歷史試飛數據進行分析，將產品的失效時間t和相應的累積失效概率F（t）利用Matlab 進行擬合[13]。

通過對全部19組航空設備（主要包括機載電子設備及機電類產品）的試飛數據分析表明，有15組數據服從指數分布，占全部數據的78.9%；有3組數據服從正態分布，占全部數據的15.8%；有1組數據服從對數正態分布，占全部數據的5.3%。指數分布的擬合結果如圖1所示。

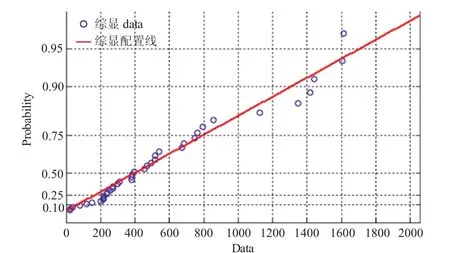
圖1 指數分布擬合結果

采用Matlab對已有航空發動機機械類構件的試飛故障數據進行了擬合。擬合結果表明：在13組數據中，有11組服從2參數威布爾分布，占全部數據的84.6%，其形狀參數的均值約為β=1.36。

因此，在采用基于2參數威布爾分布小子樣零故障壽命試驗方法對試飛階段的航空發動機進行可靠性評估以及可靠性試驗設計時，可取其形狀參數β=1.36；而對航空電子產品進行可靠性評估以及可靠性試驗設計時則可取β=1.0。

3 某型航空發動機可靠性評估及試驗示例

平均故障間隔時間既是試飛階段航空發動機基本可靠性評估參數,也是航空發動機可靠性評估優先選用的參數之一[14-15]。相關的國軍標中給出了基于指數分布的點估計值評估方法，即平均故障間隔時間的點估計值等于產品的總工作時間除以總的故障數。因此，在采用2參數威布爾分布進行航空發動機的可靠性評估及試驗設計時，可取平均故障間隔時間點估計值對應的可靠度為50%。

已知某航空發動機失效分布函數符合2參數威布爾分布，形狀參數β=1.36，要求置信度γ=80%，平均故障間隔時間要求不小于150 h，參試產品為2臺，則該航空發動機可靠度為

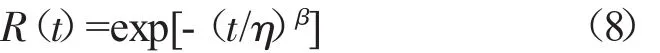
對應的特征壽命

選取2臺參試產品，從表1可以查出特征壽命的乘子λ=0.8524。由此可得，該型發動機平均故障間隔時間達到指標要求所需的無故障工作時間T=0.8524×196=167 h。

因此，當2臺該型航空發動機中最短工作時間超過167 h而未發生故障時，其平均故障間隔時間達到規定指標要求。

同樣，若已知某航空發動機的失效服從威布爾分布，其形狀參數β=1.36，置信度γ=80%，平均故障間隔時間要求不小于120 h，預計該型航空發動機的試驗時間約為142 h，則對應的特征壽命

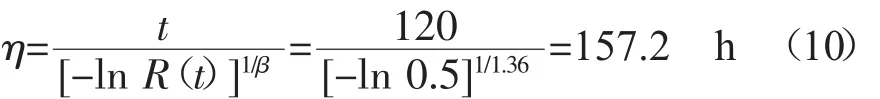
特征壽命乘子

由表2可知，此時所需的參試發動機為2臺。

4 結論

（1）小子樣零故障壽命試驗方法可用于以航空發動機為代表的高可靠性航空武器裝備在設計定型/鑒定試飛期間的可靠性定量評估及可靠性試驗設計，將可靠性的概率度量引入對試飛期間平均故障間隔時間的評估，提高了評估精度，也為可靠性試驗設計提供了新方法；

（2）形狀參數β由以往產品的失效數據和分布形式確定，與產品的失效模式有關。隨著可靠性試驗水平逐步提高以及同類或相似產品的可靠性數據的不斷豐富，有關威布爾分布的參數β以及η的取值精度會越來越高，其評估結果也會趨于精確，該方法的應用范圍也會更廣泛。

[1]金少華，李志剛，陸儉國,等.關于威布爾分布的1種參數估計方法[J].天津輕工業學院學報，2003，18（1）：43-45.JIN Shaohua，LIZhigang，LU Jianguo,etal.A parameter estimation method forWeibull distribution[J].Journal of Tianjin University of Light Industry，2003，18（1）：43-45.(in Chinese)

[2]李良巧.可靠性工程師手冊 [M].北京：中國人民大學出版社，2012：241-242.LI Liangqiao.Handbook of certified reliability engineer[M].Beijing：China Renmin University Press，2012：241-242.(in Chinese)

[3]朱壽雷，彭紹雄，董蒙.Weibull分布下的系統可靠性評估方法研究 [J].電子產品可靠性與環境試驗，2012，28（1）：20-23.ZHU Shoulei，PENG Shaoxiong，DONG Meng.Reliability evaluation ofmissile weapon systems with Weibull distribution[J].Electronic Product Reliability and Environment Testing，2012，28（1）：20-23.(in Chinese)

[4]嚴曉東，馬翔，鄭榮躍，等.三參數威布爾分布參數估計方法比較[J].寧波大學學報，2005，18（3）：301-305.YAN Xiaodong，MA Xiang，ZHENG Rongyue，et al.Comparison of the parameters estimation methods for 3 parameter Weibull distribution[J].Journal of Ningbo University，2005，18（3）：301-305.(in Chinese)

[5]鄭榮躍，嚴劍松.威布爾分布參數估計新方法研究[J].機械強度，2002，24（4）：599-601.ZHENG Rongyue，YAN Jiansong.New estimation method of three parameterWeibull distribution[J].Journal of Mechanical Strength，2002，24（4）：599-601.(in Chinese)

[6]秦明，巫世晶，彭瀟，等.1種服從威布爾分布裝備的可靠性評估方法[J].武漢大學學報，2008，41（6）：100-102.QIN Ming，WU Shijing，PENG Xiao，et al.A reliability evaluationmethod for equipmentwith aWeibull failure distribution[J].Engineering Journal of Wuhan University，2008，41（6）：100-102.(in Chinese)

[7]陸祖建，張仕念，張國彬，等.威布爾分布無故障數據的可靠性評估[J].電子產品可靠性與環境試驗，2011，29（6）：6-9.LU Zujian，ZHANG Shinian，ZHANG Guobin，et al.Reliability assessment for zero failure data in Weibull distribution[J].Electronic Product Reliability and Environment Testing，2011，29（6）：6-9.(in Chinese)

[8]趙宇，楊軍，馬小兵.可靠性數據分析教程[M].北京：北京航空航天大學出版社，2009：78-82.ZHAO Yu，YANG Jun，MA Xiaobing.Tutorial for reliability data analysis[M].Beijing：BeiHang University Press，2009：78-82.(in Chinese)

[9]陳家鼎.生存分析與可靠性 [M].北京：北京大學出版社，2005：126-130.CHEN Jiading.Survivability analysis and reliability[M].Beijing：Peking University Press，2005：126-130.(in Chinese)

[10]黃瑋，馮蘊雯，呂震宙.基于Bootstrap方法的小子樣試驗評估方法研究[J].機械科學與技術，2006，25（1）：31-35.HUANG Wei，FENG Yunwen，LYU Zhenzhou.Study on small scale sample test estimation method based on bootstrap method [J].Mechanical Science and Technology，2006，25（1）：31-35.(in Chinese)

[11]陸山，呂鴻雁.小子樣零構件可靠壽命零故障試驗評估方法[J].機械強度，2006，28（3）：411-414.LU Shan，LYU Hongyan.Assessment method of reliability life by zero failure experiments of small sample components[J].Journal of Mechanical Strength，2006，28（3）：411-414.(in Chinese)

[12]趙宇.可靠性數據分析[M].北京：國防工業出版社，2011：34-35.ZHAO Yu.Data analysis of reliability[M].Beijing：National Defense Industry Press，2011：34-35.(in Chinese)

[13]賀國芳，許海寶.可靠性數據的收集與分析[M].北京：國防工業出版社，1995：39-41.HEGuofang，XU Haibao.Collection and analysis of reliability data [M].Beijing：National Defense Industry Press，1995：39-41.(in Chinese)

[14]謝靜，范文正，謝鎮波，等.某型軍用發動機使用可靠性評估[J].航空發動機，2012，38（6）：43-47.XIE Jing，FAN Wenzheng，XIE Zhenbo，et al.Evalution of military engine service reliability[J].Aeroengine，2012，38（6）：43-47.(in Chinese)

[15]徐可君，江龍平.軍用航空發動機可靠性和壽命管理[J].中國工程科學，2003，5（1）：82-88.XU Kejun，JIANG Longping.Reliability and life cyclemanagement of military aeroenging [J].Engineering Science，2003，5（1）：82-88.(in Chinese)

烏克蘭AI-436T12發動機

AI-436T12發動機于2005年由烏克蘭的伊夫琴科-前進設計局聯合馬達-西奇公司以及俄羅斯的禮炮公司、烏法發動機生產聯合體、喀山發動機生產聯合體等單位共同開始研制，禮炮公司為主生產單位。AI-436-T12發動機的研制預計花費45～60億美元，主要依靠國家支持以及私企和國企的投資，計劃在2015～2017年完成研制工作。

AI-436T12發動機是技術成熟的D-436T1發動機的深度改型，曾用代號D-436-TX，除了計劃配裝中短程干線客機MS-21外，還可用于配裝俄印聯合研制的多功能運輸機（MTA）等飛機。

AI-436-T12發動機結構設計中采用了許多新技術方案，如帶寬弦無凸肩葉片的風扇、齒輪傳動減速器、新型壓氣機、新型燃燒室、帶陶瓷涂層的渦輪葉片等，可以保證飛機具有高的燃油效率、合理的價格和低水平的噪聲，污染物排放水平滿足最嚴格的環保標準要求。

AI-436-T12發動機的性能參數：起飛狀態推力為117.6 kN，耗油率為0.272 kg/daN·h，空氣流量為557.3 kg/s，涵道比為10.25，增壓比為26.33，燃氣溫度為 1568 K；最大巡航狀態（H=11 km，Ma=0.8）推力為23.5 kN，耗油率為0.554 kg/daN·h；風扇直徑為2070mm，凈質量為2250 kg，發動機質推比為0.188 kg/daN。

（中航工業動力所 劉 靜）

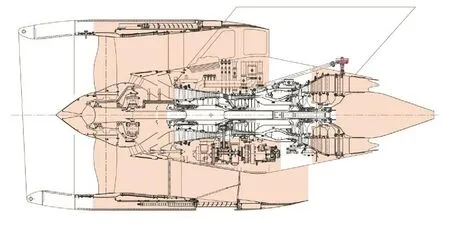
AI-436T12發動機結構

Reliability AssessmentMethod and Test Scheme Design During Flight Test

GAO Ya-juan1,LU Shan2
（1.Chinese Flight Test Establishment，Xi'an 710089,China； 2.Schoolof Power and Energy,Northwestern Polytechnical University,Xi'an 710072,China）

A zero-failure life testmethod for small sample component based on two-parameterWeibull distribution was proposed to solvemean time between failure assessment issues ofhigh reliability aeronautical products such as aeroengines,also to design the flight test and ground test scheme during qualification and type approval process.The coefficients used for reliability assessment and test scheme design were calculated and the tabulations were included.Then shape parameter was derived through curve fitting analysis of aeroengine historical flight test scheme data by Matlab.At last,the applicability and validity ofmethod was verified by reliability assessment and test scheme design of an aeroengine.The result shows that themethod could apply to solving reliability assessment and test scheme design for high reliability aeronautical products.

reliability assessment;aeroengine;zero-failure life testmethod for small sample component;Weibull distribution;aviation weapon equipment

V263.3

A

10.13477/j.cnki.aeroengine.2014.03.014

2014-01-26

高雅娟（1981），女，碩士，研究方向為航空發動機可靠性和維修性評估驗證；E-mail：tigerwangjianfeng@163.com。

高雅娟，陸山.試飛階段可靠性評估方法及試驗方案設計[J].航空發動機，2014，40（3）：66-70.GAOYajuan，LUShan.Reliability assessment method and testscheme design duringflight test[J].Aeroengine，2014，40（3）：66-70.