徑流時(shí)間序列復(fù)雜網(wǎng)絡(luò)的動(dòng)力學(xué)拓?fù)湫再|(zhì)

唐 強(qiáng)，胡鐵松

?

徑流時(shí)間序列復(fù)雜網(wǎng)絡(luò)的動(dòng)力學(xué)拓?fù)湫再|(zhì)

唐 強(qiáng)1，胡鐵松2

（1. 武漢紡織大學(xué) 數(shù)學(xué)與計(jì)算機(jī)學(xué)院，湖北 武漢 430200；2. 武漢大學(xué) 水資源與水電工程科學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室，湖北 武漢 430072）

以金沙江和美國(guó)Ocumlgee河日徑流序列為對(duì)象，利用復(fù)雜網(wǎng)絡(luò)理論對(duì)徑流序列的波動(dòng)性特征進(jìn)行了初步探討。通過粗粒化方法將徑流時(shí)間序列轉(zhuǎn)化為符號(hào)序列，進(jìn)而構(gòu)建相應(yīng)的復(fù)雜網(wǎng)絡(luò)。對(duì)網(wǎng)絡(luò)的聚類系數(shù)、平均路徑長(zhǎng)度和中介中心性測(cè)度等動(dòng)力學(xué)統(tǒng)計(jì)特征量和拓?fù)鋮?shù)的討論發(fā)現(xiàn)，網(wǎng)絡(luò)的聚類系數(shù)較大而平均路徑長(zhǎng)度較小，不同的波動(dòng)模式之間存在著短程相關(guān)性；不同頂點(diǎn)的中介中心性測(cè)度具有明顯的差異，表明某些頂點(diǎn)所代表的波動(dòng)模式有著重要的意義，在一定程度上可以作為各種波動(dòng)模式之間轉(zhuǎn)換的前兆。這些結(jié)論有助于更好地把握徑流變化的規(guī)律，對(duì)于徑流的短期預(yù)測(cè)具有一定的參考價(jià)值。

徑流序列；波動(dòng)性；復(fù)雜網(wǎng)絡(luò)；粗粒化；聚類系數(shù)；平均路徑長(zhǎng)度；中介中心性測(cè)度

徑流過程是一種重要的水文現(xiàn)象，借助各種時(shí)間序列的分析方法研究徑流序列的性質(zhì)，提取所需信息，揭示其內(nèi)在規(guī)律對(duì)于水資源的利用有著重要的意義，長(zhǎng)期以來受到眾多研究人員的重視。非線性科學(xué)的發(fā)展，為徑流過程的定量分析與研究提供了新的理論和方法，人們利用混沌、分形和小波等非線性理論對(duì)徑流序列進(jìn)行了研究，試圖解釋序列波動(dòng)的原因和機(jī)理，并對(duì)其未來的變化趨勢(shì)做出預(yù)測(cè)，幾十年來取得了豐碩的成果[1-6]。

由于河川徑流受到自然環(huán)境、社會(huì)條件和人類活動(dòng)多重制約，同時(shí)又存在著各種尺度關(guān)聯(lián)和各種波動(dòng)，具有高度的復(fù)雜性，需要利用多種方法，從不同的角度來進(jìn)行討論。上個(gè)世紀(jì)90年代興起的復(fù)雜網(wǎng)絡(luò)理論為徑流過程的研究提供了一種新的思路[7-9]。

在本文中，我們以金沙江屏山站與佐治亞州Ocumlgee河Macon站日徑流時(shí)間序列作為研究對(duì)象，首先運(yùn)用等概率粗粒化方法，將徑流序列轉(zhuǎn)化為復(fù)雜網(wǎng)絡(luò)，把徑流序列波動(dòng)信息編碼在網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)之中；隨后通過對(duì)網(wǎng)絡(luò)的動(dòng)力學(xué)統(tǒng)計(jì)特征量和拓?fù)鋮?shù)等進(jìn)行分析，獲取徑流波動(dòng)網(wǎng)絡(luò)的內(nèi)在規(guī)律性，從復(fù)雜網(wǎng)絡(luò)的角度解釋徑流變化的動(dòng)力學(xué)特征。

1 徑流時(shí)間序列的粗粒化處理

郝柏林提出可以通過符號(hào)動(dòng)力學(xué)建立運(yùn)動(dòng)軌道和形式語(yǔ)言的聯(lián)系，然后借助語(yǔ)法復(fù)雜性理論來刻畫復(fù)雜性，其核心內(nèi)容就是符號(hào)動(dòng)力學(xué)與時(shí)間序列的粗粒化和符號(hào)化[10]。粗粒化常用的方法是對(duì)系統(tǒng)區(qū)間進(jìn)行同質(zhì)劃分[11]，將整個(gè)區(qū)間分成有限個(gè)子區(qū)間。如果對(duì)劃分后的每個(gè)子區(qū)間賦予一個(gè)符號(hào)，則整個(gè)系統(tǒng)區(qū)間就轉(zhuǎn)換為一個(gè)符號(hào)序列，對(duì)粗粒化符號(hào)序列的研究也就是對(duì)相應(yīng)時(shí)間序列的研究。由于粗粒化過程舍去了小層次上的細(xì)節(jié)，粗粒化形式的符號(hào)序列又具有有限性，這就使得粗粒化方法能突出系統(tǒng)的本質(zhì)的特征。

粗粒化的精度對(duì)結(jié)論的有效性有很大的影響，這就要求在進(jìn)行符號(hào)轉(zhuǎn)換時(shí)，確定的符號(hào)種類不能太多，每一個(gè)符號(hào)要盡可能代表系統(tǒng)變化中的某一種基本的、相對(duì)獨(dú)立的模式。常見的粗粒化方法有二值粗粒化、多值粗粒化和等概率粗粒化等方法[12, 13]。

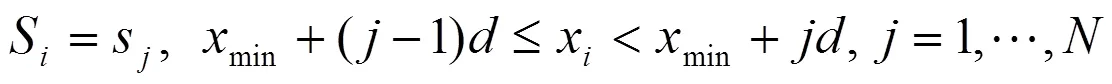
多值粗粒化方法沒有考慮不同的符號(hào)在符號(hào)序列中出現(xiàn)的概率，等概率粗粒化方法可以使得不同的符號(hào)在符號(hào)序列中出現(xiàn)的概率相同。記日徑流序列為{(),=1,…,}，首先計(jì)算徑流量的波動(dòng)()：

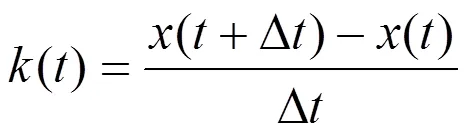
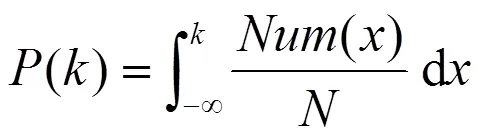
其中()為對(duì)應(yīng)一種徑流量波動(dòng)模態(tài)發(fā)生的次數(shù)[13]。按照等概率的思想，我們將徑流量的波動(dòng)()分為4個(gè)區(qū)間，定義4個(gè)特征字符

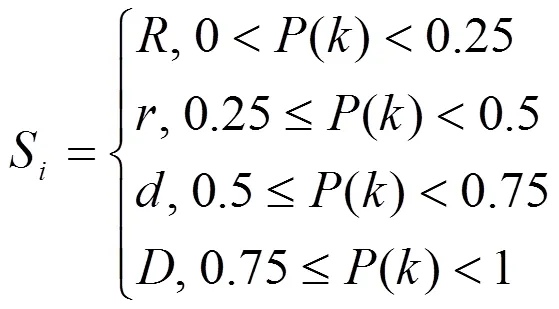
其中，代表徑流量快速增加，代表徑流量緩慢增加，代表徑流量緩慢降低，代表徑流量快速降低。這樣就可以將徑流序列轉(zhuǎn)化為符號(hào)序列：

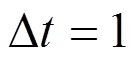
2 復(fù)雜網(wǎng)絡(luò)的構(gòu)建

將時(shí)間序列粗粒化處理后，可以得到由4個(gè)字符{,,,}構(gòu)成的符號(hào)序列。在符號(hào)序列中，稱由個(gè)字符構(gòu)成的字串為字串。理論上不同的字串共有4種。在符號(hào)序列的分析中，相互連接的字符的基本模式稱為元結(jié)構(gòu)。這些字串即為符號(hào)序列的元結(jié)構(gòu)，代表了各種波動(dòng)模式。符號(hào)序列表現(xiàn)了一種波動(dòng)模式向另一種波動(dòng)模式的轉(zhuǎn)變，這種轉(zhuǎn)變體現(xiàn)了各種波動(dòng)模式之間的信息傳遞等關(guān)系，具有多元化的特征。后一個(gè)模式的出現(xiàn)是以前一個(gè)或多個(gè)模式為基礎(chǔ)的，體現(xiàn)了一定的記憶性，因此模式之間的聯(lián)系是“有向”的，聯(lián)系的強(qiáng)弱程度也各不相同。因此，我們構(gòu)建一個(gè)有向加權(quán)網(wǎng)絡(luò)來描述各種波動(dòng)模式之間的關(guān)系。

當(dāng)下，越來越多的汽車制造商和零部件制造商希望將工業(yè)服務(wù)外包，以獲得專業(yè)高效的服務(wù)，提升設(shè)備運(yùn)行的可靠性，提高企業(yè)的生產(chǎn)能力和運(yùn)營(yíng)效率，從而將更多的精力集中到市場(chǎng)調(diào)研、產(chǎn)品研發(fā)、產(chǎn)品質(zhì)量提升以及生產(chǎn)工藝研究等核心業(yè)務(wù)上。

將每一個(gè)字串視為網(wǎng)絡(luò)的一個(gè)頂點(diǎn)，符號(hào)序列中相鄰的兩個(gè)字串之間存在一條邊，由前一個(gè)字串指向后一個(gè)字串。如果兩個(gè)頂點(diǎn)和之間存在多條邊，則邊數(shù)即為這兩個(gè)頂點(diǎn)之間邊的權(quán)重w。

3 徑流網(wǎng)絡(luò)的性質(zhì)

分別以金沙江屏山站1943年1月1號(hào)至1992年12月31號(hào)日徑流時(shí)間序列與美國(guó)佐治亞州Ocumlgee河Macon站1958年1月1號(hào)至2007年12月31號(hào)日徑流時(shí)間序列作為研究對(duì)象。金沙江屏山站徑流序列來源于長(zhǎng)江水利委員會(huì)水文局，共有18263個(gè)數(shù)據(jù)；Ocumlgee河Macon站徑流序列來源于美國(guó)地質(zhì)調(diào)查局網(wǎng)站 http://water.usgs.gov/ waterwatch/，含18250個(gè)數(shù)據(jù)。

3.1 聚類系數(shù)

對(duì)于有向加權(quán)網(wǎng)絡(luò)，當(dāng)考慮邊的權(quán)重的時(shí)候，網(wǎng)絡(luò)的某個(gè)頂點(diǎn)的聚類系數(shù)定義為[14]

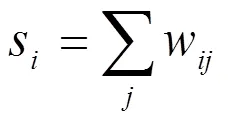
圖 1 給出了網(wǎng)絡(luò)頂點(diǎn)的聚類系數(shù)與度值的關(guān)系。從圖1中可以看出，兩個(gè)網(wǎng)絡(luò)頂點(diǎn)的聚類系數(shù)隨度值的變化都較大，這意味著三個(gè)網(wǎng)絡(luò)并不是完全隨機(jī)的，而是在某種程度上具有類似于社會(huì)關(guān)系網(wǎng)絡(luò)中“物以類聚，人以群分”的特性[15]。Ocumlgee 河日徑流波動(dòng)網(wǎng)絡(luò)度值較小的頂點(diǎn)聚類系數(shù)較大，度值較大的聚類系數(shù)較小，不同于小世界網(wǎng)絡(luò)的性質(zhì)。聚類系數(shù)的這種性質(zhì)說明網(wǎng)絡(luò)的群聚特性既可能會(huì)發(fā)生在小的集團(tuán)中，也可能會(huì)發(fā)生在大的集團(tuán)中。對(duì)于隨時(shí)間變化的徑流來說，意味著群發(fā)性有時(shí)會(huì)反映在小的時(shí)間尺度上，有時(shí)又會(huì)反映在大的時(shí)間尺度上，即徑流變化有多年的周期波動(dòng)，又有年度的漲落，還有月的變化特征。而金沙江日徑流波動(dòng)網(wǎng)絡(luò)聚類系數(shù)與度值的關(guān)系則正好相反，表明群發(fā)性更多的發(fā)生在大的集團(tuán)中，徑流變化的長(zhǎng)期周期波動(dòng)更明顯。

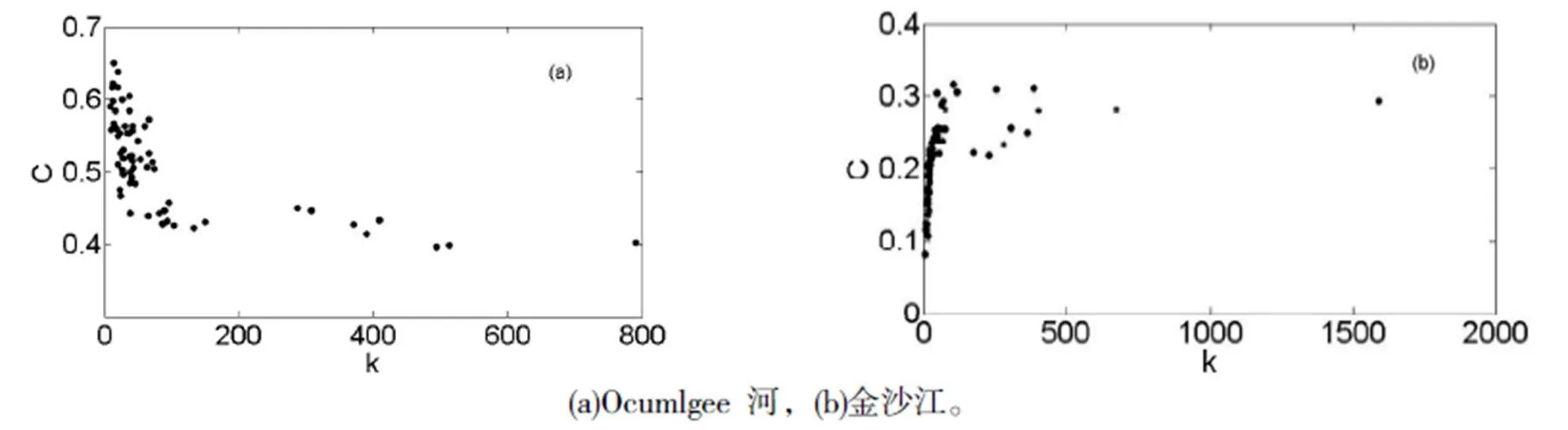
圖1 日徑流波動(dòng)網(wǎng)絡(luò)頂點(diǎn)的聚類系數(shù)與度值的關(guān)系

3.2 平均路徑長(zhǎng)度

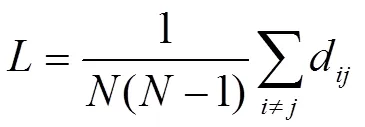
其中為頂點(diǎn)總數(shù)，d為頂點(diǎn)和的距離。表1給出了兩個(gè)網(wǎng)絡(luò)的平均聚類系數(shù)和平均路徑長(zhǎng)度。

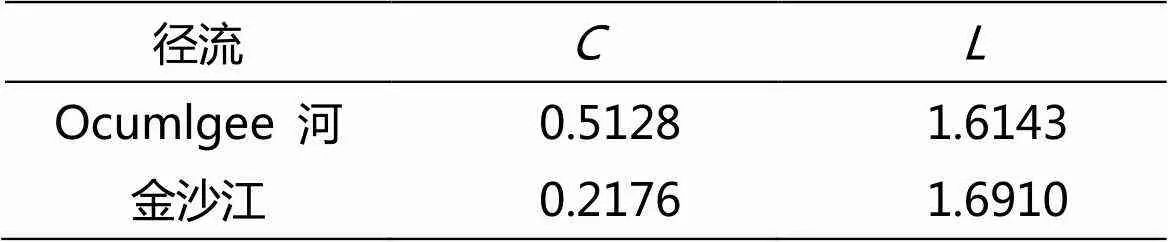
表1 網(wǎng)絡(luò)的平均聚類系數(shù)與平均路徑長(zhǎng)度

由表1可知，兩條河流的日徑流波動(dòng)網(wǎng)絡(luò)均具有較大的平均聚類系數(shù)和較小的平均路徑長(zhǎng)度。平均路徑長(zhǎng)度表征了由一種波動(dòng)模式轉(zhuǎn)變?yōu)榱硪环N波動(dòng)模式所花的時(shí)間，網(wǎng)絡(luò)的平均路徑長(zhǎng)度均小于 2，表明模式的轉(zhuǎn)換時(shí)間大約為6天左右，表現(xiàn)出短程相關(guān)性，這對(duì)于徑流的短期預(yù)測(cè)具有一定的參考價(jià)值。較大的平均聚類系數(shù)表明各種波動(dòng)模式存在小規(guī)模的群簇，群簇內(nèi)部頂點(diǎn)之間的關(guān)聯(lián)較好。如不同的季節(jié)內(nèi)可能是不同的波動(dòng)模式占主要地位，這些波動(dòng)模式就構(gòu)成一個(gè)群簇，不同的影響因素對(duì)應(yīng)不同的群簇。Ocumlgee 河流日徑流波動(dòng)網(wǎng)絡(luò)的平均聚類系數(shù)較大，平均路徑長(zhǎng)度較小，表明它的群簇性明顯，模式轉(zhuǎn)換較頻繁。

3.3 中介中心性

在一個(gè)網(wǎng)絡(luò)中，不同的頂點(diǎn)一般具有不同的重要性。頂點(diǎn)的拓?fù)渲匾缘葍r(jià)于該頂點(diǎn)與其他頂點(diǎn)的連接性，這種拓?fù)渲匾钥梢杂弥薪橹行男詠砜坍媅17, 18]。

信息在網(wǎng)絡(luò)中的流通和傳遞往往要通過少數(shù)關(guān)鍵頂點(diǎn)才能以最短路徑到達(dá)網(wǎng)絡(luò)中的其他頂點(diǎn)，失去這些關(guān)鍵頂點(diǎn)將對(duì)網(wǎng)絡(luò)的整體性質(zhì)造成較大的影響。在復(fù)雜網(wǎng)絡(luò)理論中, 用中心性來衡量一個(gè)頂點(diǎn)在網(wǎng)絡(luò)中影響能力的大小，即獲得、控制信息的能力。中介中心性反映了頂點(diǎn)在網(wǎng)絡(luò)中的中介性和樞紐程度[19]。

網(wǎng)絡(luò)中一個(gè)頂點(diǎn)的中介中心性測(cè)度g定義如下：設(shè)(,)為頂點(diǎn)對(duì)(,)之間所有最短路徑的總數(shù)，路徑的長(zhǎng)度就是路徑通過的各條邊的權(quán)重之和。在這些路徑中通過中間頂點(diǎn)的路徑數(shù)記為c(,)，記

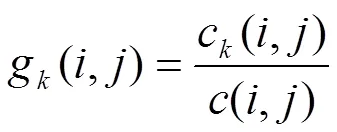
則頂點(diǎn)的中介中心性測(cè)度g為所有頂點(diǎn)對(duì)的g(,)之和，即

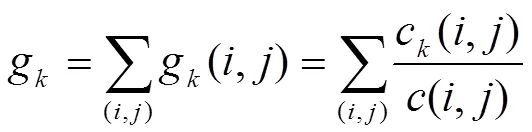
我們計(jì)算了兩個(gè)網(wǎng)絡(luò)各頂點(diǎn)的中介中心性測(cè)度，并對(duì)它們進(jìn)行了排序，結(jié)果如表2、表3所示。從中可見，不同頂點(diǎn)的中介中心性測(cè)度有較大的差異。Ocumlgee河日徑流波動(dòng)網(wǎng)絡(luò)前 30 個(gè)頂點(diǎn)對(duì)整個(gè)網(wǎng)絡(luò)的中介中心性的貢獻(xiàn)率達(dá)到了 85.03%，前10個(gè)頂點(diǎn)的g都在3%以上，中介中心性的貢獻(xiàn)率達(dá)到41%。金沙江日徑流波動(dòng)網(wǎng)絡(luò)前40個(gè)頂點(diǎn)對(duì)整個(gè)網(wǎng)絡(luò)的中介中心性的貢獻(xiàn)率達(dá)到了85.65%，前 7 個(gè)頂點(diǎn)的g都在3%以上，中介中心性的貢獻(xiàn)率達(dá)到26%。這些貢獻(xiàn)率較大的頂點(diǎn)的中介中心性等級(jí)與g%的雙對(duì)數(shù)曲線圖表明與g%呈冪律關(guān)系，如圖2所示。這意味著某些頂點(diǎn)所代表的波動(dòng)模式有著重要的意義，任意兩個(gè)波動(dòng)模式之間的轉(zhuǎn)換經(jīng)過這幾個(gè)波動(dòng)模式中轉(zhuǎn)的概率較大，它們?cè)谝欢ǔ潭壬峡梢宰鳛楦鞣N波動(dòng)模式之間轉(zhuǎn)換的前兆，對(duì)波動(dòng)模式的轉(zhuǎn)換具有重要的意義，對(duì)它們的研究將有助于更好地把握徑流變化的規(guī)律。此外，在Ocumlgee河日徑流波動(dòng)網(wǎng)絡(luò)中，、和三種波動(dòng)模式的g% 均在5%以上，說明了該徑流波動(dòng)急劇增加和急劇降低模式的重要性，反映了該徑流波動(dòng)的劇烈化程度。

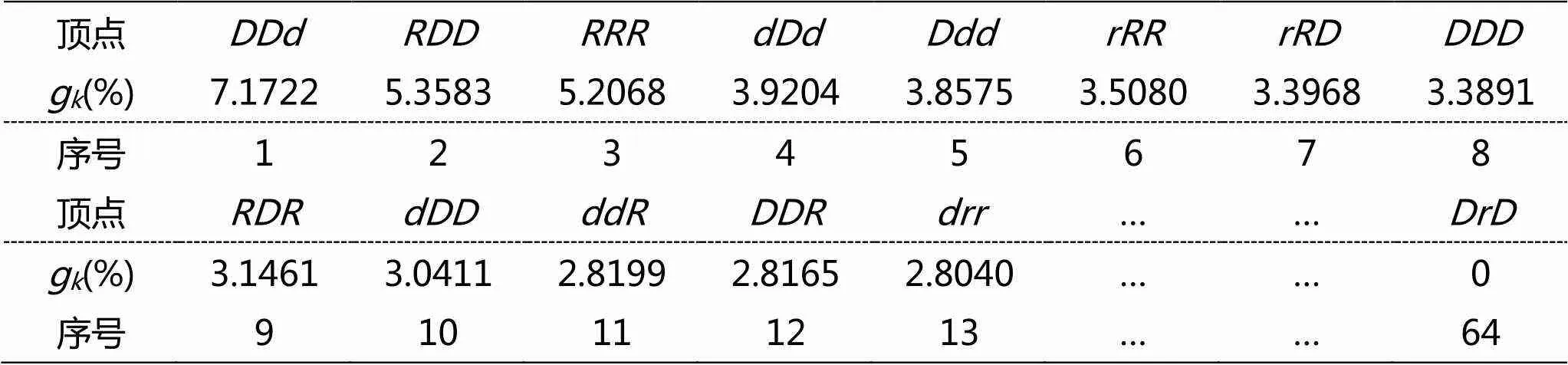
表2 Ocumlgee河Macon站日徑流波動(dòng)網(wǎng)絡(luò)各頂點(diǎn)的中介中心性測(cè)度

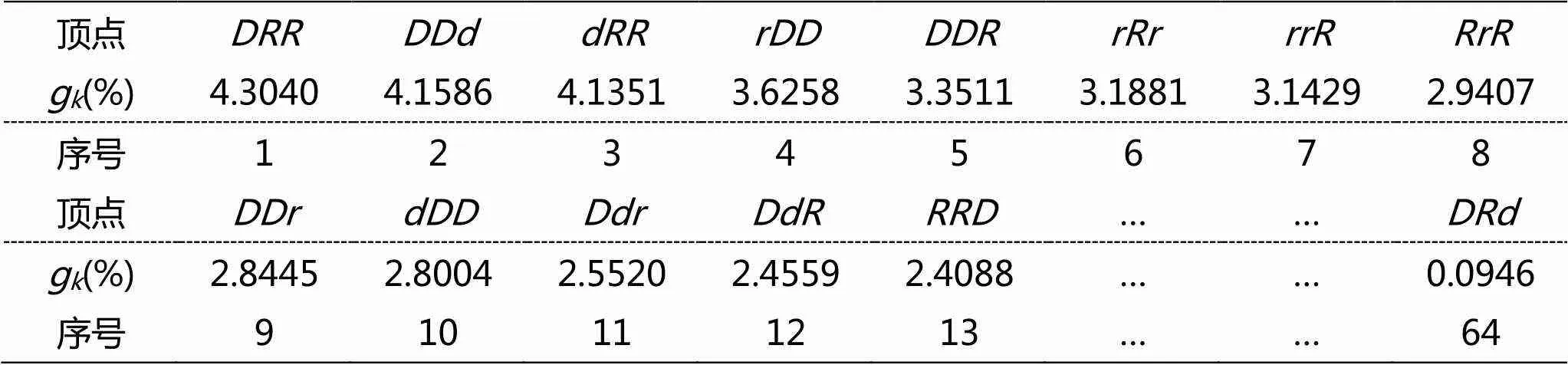
表3 金沙江屏山站日徑流波動(dòng)網(wǎng)絡(luò)各頂點(diǎn)的中介中心性測(cè)度

圖2 頂點(diǎn)的中介中心性等級(jí)與測(cè)度的關(guān)系。

4 結(jié)論

本文通過粗粒化方法將徑流序列轉(zhuǎn)化為符號(hào)序列，進(jìn)而構(gòu)建相應(yīng)的復(fù)雜網(wǎng)絡(luò)。通過對(duì)網(wǎng)絡(luò)的聚類系數(shù)、平均路徑長(zhǎng)度和中介中心性測(cè)度等動(dòng)力學(xué)統(tǒng)計(jì)特征量和拓?fù)鋮?shù)的討論發(fā)現(xiàn)，金沙江屏山站與Ocumlgee河Macon站日徑流過程不是隨機(jī)的過程，存在少數(shù)幾種重要的波動(dòng)模式。波動(dòng)網(wǎng)絡(luò)均具有較大的聚類系數(shù)和較小的平均路徑長(zhǎng)度，不同的波動(dòng)模式之間存在著短程相關(guān)性，各種波動(dòng)模式存在小規(guī)模的群簇，不同的群簇對(duì)應(yīng)不同的影響因素，群簇內(nèi)部頂點(diǎn)之間的關(guān)聯(lián)較好，這對(duì)于徑流的短期預(yù)測(cè)具有一定的參考價(jià)值。Ocumlgee 河流日徑流波動(dòng)網(wǎng)絡(luò)頂點(diǎn)的度值和聚類系數(shù)呈負(fù)相關(guān)關(guān)系，說明徑流變化有多年的周期波動(dòng)，又有年度的漲落，還有月的變化特征。Ocumlgee 河日徑流波動(dòng)網(wǎng)絡(luò)中、和三種波動(dòng)模式的中介中心性測(cè)度較大，說明了該徑流波動(dòng)急劇增加和急劇降低模式的重要性，反映了該徑流劇烈波動(dòng)較頻繁。不同頂點(diǎn)的中介中心性測(cè)度具有明顯的差異，這意味著某些頂點(diǎn)所代表的波動(dòng)模式有著重要的意義，在一定程度上可以作為各種波動(dòng)模式之間轉(zhuǎn)換的前兆，對(duì)它們的研究將有助于更好地把握徑流變化的規(guī)律。

[1] 王文均，葉敏，陳顯維. 長(zhǎng)江徑流時(shí)間序列混濁特性的定量分析[J]. 水科學(xué)進(jìn)展，1994，5(2)：87-93.

[2] 侯玉，吳伯賢，鄧國(guó)權(quán)．分形理論用于洪水分期的初步探討[J]．水科學(xué)進(jìn)展，1999，10(2): 140-143．

[3] Wang W, Vrijling J K, Gelder V, et al. Testing for nonlinearity of streamflow processes at different timescales[J]. Journal of Hydrology, 2006, 322: 247-268.

[4] Bof L H, Pruski F F, Da Silva L M, et al. Analysis of appropriate timescale for water diversion permits in Brazil[J]．Environmental Management, 2013, 51(2): 492-500 .

[5] 李新杰，胡鐵松，郭旭寧，等. 0-1 測(cè)試方法的徑流時(shí)間序列混沌特性應(yīng)用[J]. 水科學(xué)進(jìn)展，2012，32（6）：875-882.

[6] Khatibir, Sivakumarb, Ghorbanima, et al. Investigating chaos in river stage and discharge time series[J]．Journal of Hydrology，2012，414-415：108-117.

[7] Watts, D.J., S.H. Strogatz. Collective dynamics of small world networks [J]．Nature, 1998, 393: 440-442.

[8] Barabási, A.L., R. Albert. Emergence of scaling in random networks [J]．Science, 1999, 286(5439): 509-512.

[9] Qiang Tang，Jie Liu，Honglin Liu. Comparison of different daily streamflow series in US and CHINA, under a viewpoint of complex networks[J]．Modern Physics Letters B, 2010, 24(14): 1541-1547.

[10]郝柏林．復(fù)雜性的刻畫與“復(fù)雜性科學(xué)”[J]．科學(xué)，1999，51(3): 3-8．

[11]Wackerbauer, R., A. Witt, H. Atmanspacher, et al. A comparative classification of complexity measures [J]．Chaos, Solitons & Fractals, 1994, 4(1): 133-173.

[12]張佃中，譚小紅，王智，等．基于等概率粗粒化的復(fù)雜度算法及其應(yīng)用[J]．系統(tǒng)仿真學(xué)報(bào)，2008，20(15): 4096-4098．

[13]周磊，龔志強(qiáng)，支蓉，等．利用復(fù)雜網(wǎng)絡(luò)研究中國(guó)溫度序列的拓?fù)湫再|(zhì)[J]．物理學(xué)報(bào)，2008，57(11): 7380-7389．

[14]陳衛(wèi)東，徐華，郭琦．國(guó)際石油價(jià)格復(fù)雜網(wǎng)絡(luò)的動(dòng)力學(xué)拓?fù)湫再|(zhì)[J]．物理學(xué)報(bào)，2010，59(7): 4514-4523．

[15]汪小帆，李翔，陳關(guān)榮．復(fù)雜網(wǎng)絡(luò)理論及其應(yīng)用[M]．北京：清華大學(xué)出版社，2006．

[16]何大韌，劉宗華，汪秉宏．復(fù)雜系統(tǒng)與復(fù)雜網(wǎng)絡(luò)[M]．北京：高等教育出版社，2009．

[17]Freeman, L.C.. Centrality in social networks conceptual clarification [J]．Social Networks, 1978, 1(3): 215-239.

[18]Li P., B.H. Wang. Extracting hidden fluctuation patterns of Hang Seng stock index from network topologies [J]．Physica A, 2007, 378(2): 519-526.

[19]Goh, K.I., E. Oh, B. Kahng, et al.Betweenness centrality correlation in social networks [J]．Physical Review E, 2003, 67: 017101.

Dynamic Analysis on the Topological Properties of the Complex Network of Runoff Time Series

TANG Qiang1, HU Tie-song2

(1. School of Mathematics & Computer Science, Wuhan Textile University, Wuhan Hubei 430200, China; 2.State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan Hubei 430072, China.)

Based on the complex networks theory, daily runoff series of the Jinsha River in China and the Ocumlgee River in America are used for exploring the fluctuation characteristic of this runoff.A runoff time series can be transformed into a discrete symbolic sequence by preprocessing coarse graining, and a complex network will be created. Then some dynamic statistical features and topology parameters of two fluctuation networks, such as clustering coefficient, mean path length and betweenness centrality, are discussed. We find that the clustering coefficients of two networks are larger and mean path lengths are smaller, which indicates the short-range correlation exists in different fluctuation patterns. The betweenness centrality of different nodes have obvious difference, which means that some fluctuation patterns have important significance and can be as a conversion precursor between the various fluctuation patterns to some extent. These results contribute to understanding the variation of runoff process and have reference value for short-term prediction of runoff process.

Runoff Time Series; Fluctuation; Complex Networks; Coarse Graining; Clustering Coefficient; Mean Path Length; Betweenness Centrality

唐強(qiáng)（1974-），男，副教授，研究方向：時(shí)間序列非線性性質(zhì).

P333

A

2095－414X(2014)03－0087－05