基于合同儲備的軍地物資聯儲經濟分析

龍綿偉，荀 燁，陳新民

(1.軍事交通學院 軍事物流系，天津300161;2.軍事交通學院 研究生管理大隊，天津300161)

依托國家、地方和社會資源，實現軍民結合的戰備物資儲備，是深化軍隊戰備物資儲備改革的發展趨勢［1］。合同儲備是繼軍隊自主式實物儲備和“以廠代儲”模式之后出現的又一種新型儲備模式，是軍民融合式物資儲備模式的重要組成部分［2］。本文運用經濟學有關理論方法，分析了基于合同儲備的軍地聯儲模式在經濟上的可行性及其應當達到的臨界條件。

1 合同儲備的概念及分類

合同儲備是指由軍隊與地方單位簽訂合同，軍隊在平時按合同約定給予地方代儲單位或生產企業一定的經濟補貼，地方代儲單位或生產企業根據合同在平時履行代儲責任或保留一定的生產能力，保證在約定的時限內完成物資的籌措或生產并以市價供應軍隊或政府［3］。根據戰備物資在企業中的存在形態，戰備物資合同儲備可以分為無產權實物合同儲備和生產能力合同儲備［2-3］。軍隊無產權實物儲備是軍隊根據市場通行規則給地方單位支付一定數額的定金，軍隊沒有物資的所有權而只擁有物資的優先使用權，地方代儲單位以實物的形式按軍隊要求完成物資儲備，當軍隊需要時以市價供應軍隊。生產能力合同儲備是為保證緊急狀態下物資供應，在軍隊提供適量補貼的前提下，由生產相似物品的單位根據軍隊需要保有一定的生產能力儲備，如人員、場地、生產線、原料等，確保在軍隊提出需求后能在短時間內完成轉產，并按預定的生產速度生產儲備物資，以市價供應軍隊。

2 基于合同儲備的軍地聯儲模型構建

2.1 問題分析

基于合同儲備的軍地聯儲有軍隊與合同企業實物儲備，軍隊實物儲備與合同企業生產能力儲備，軍隊與合同企業實物、生產能力儲備3 種形式。本文從軍隊與合同企業實物、生產能力儲備這種最復雜的情況出發進行分析研究。在這種儲備模式下，物資供應鏈由合同企業和軍隊組成。軍隊和合同企業共同進行部分物資實物儲備，同時，軍隊以生產能力補貼的方式使企業保有一定物資生產能力儲備。軍隊儲備、合同企業實物儲備和合同企業生產能力儲備，除了儲備成本不同之外，其對物資需求保障能力也是不同的;因此，區別于單一儲備主體的儲備模式，在該儲備模式下，引入保障能力參數，綜合保障能力和儲備成本2 方面因素做出物資儲備量的決策。

2.2 問題假設

(1)假設軍隊儲備和合同企業實物儲備、生產能力儲備的成本結構、收益函數及物資需求分布函數是共同知識。

(2)假設軍隊及合同企業的實物儲備全部用于滿足物資需求，合同企業根據實物儲備不足部分進行生產。也就是說，期末軍隊及合同企業的實物儲備物資庫存量為零。

(3)軍隊只向合同企業支付已使用物資的采購價款。

令D1為物資總儲備量，λ1D1為軍隊儲備量，λ2D1為合同企業實物儲備量，(1-λ1-λ2)D1為合同企業生產能力儲備量。

令P為單位物資價格，由外部市場環境決定;C1為合同企業單位物資生產成本(包括原材料購買成本、生產費用、運輸費用等);C2為軍隊單位物資庫存成本;C'2為合同企業單位物資庫存成本;g為合同企業物資儲備不足時的單位懲罰成本;C3為合同企業實物儲備補貼，C3=a+αλ2D1λ2D1。其中:a為實物儲備固定補貼;α 為實物儲備補貼浮動系數，α 的取值為儲備量λ2D1的分段函數。

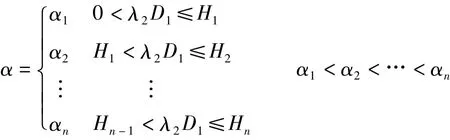
C4為物資生產能力儲備補貼，C4=b+β(1-λ1-λ2)D1(1-λ1-λ2)D1。其中:b為生產能力儲備固定補貼;β 為生產能力儲備補貼浮動系數，β的取值為物資生產能力儲備量(1-λ1-λ2)D1的分段函數。

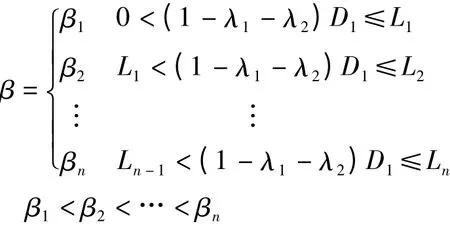
C'4為合同企業保有生產能力儲備的成本，C'4=c+ε(1-λ1-λ2)D1。其中:c為合同企業保有生產能力儲備的固定成本;ε 為保有生產能力儲備成本浮動系數。C5為軍隊與合同企業實物儲備不能滿足需求時，采用其他方式獲取單位物資的成本。

ω 為軍隊儲備單位物資的保障能力系數;φω為合同企業實物儲備單位物資的保障能力系數，且0 ＜φ ＜1;φω 為合同企業生產能力儲備單位物資的保障能力系數，且0 ＜φ ＜φ ＜1;γω 為單位物資最低保障能力臨界系數。

D為物資需求，其分布函數為F(F為隨機分布函數)，概率密度函數為f，D∈(0，Dh)。滿足條件:F是連續可微且嚴格增加，F(0)=0，F(Dh)=1 ，設是需求的期望［4］。為不失一般性，假設C1＜P＜C5。

2.3 模型構建

當軍隊儲備量為λ1D1，合同企業實物儲備量為λ2D1時，合同企業生產能力儲備量為(1-λ1-λ2)D1時，合同企業的利潤期望為

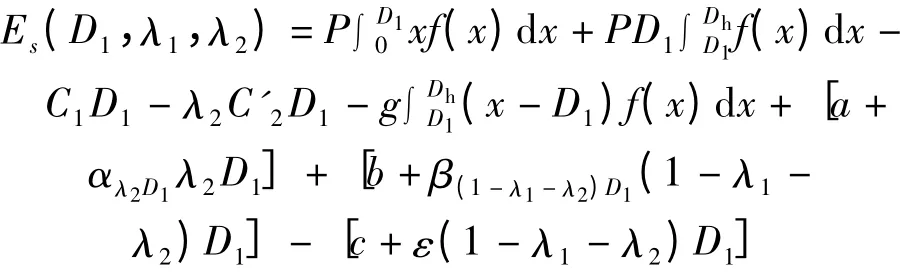
軍隊利潤期望為

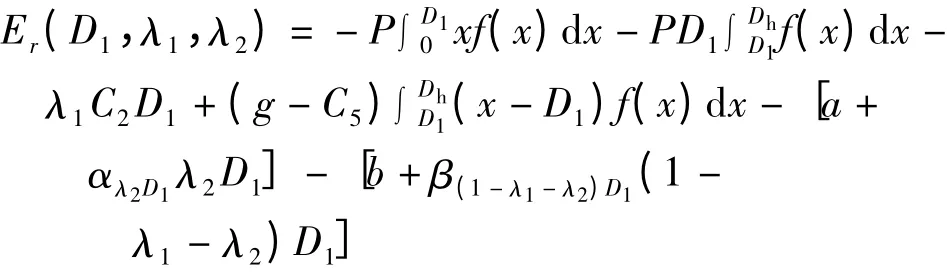
整個供應鏈的利潤期望為

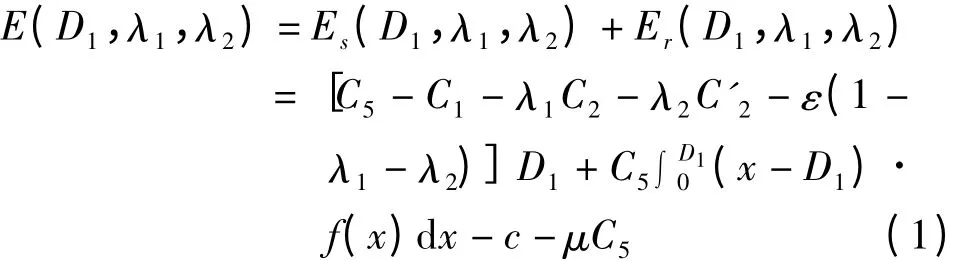
該供應鏈對物資需求的保障能力為W=ωλ1D1+φωλ2D1+ φω(1-λ1-λ2)D1，理想的物資供應鏈應該使供應鏈的利潤期望達到最大，同時對需求的保障能力也達到最大，即

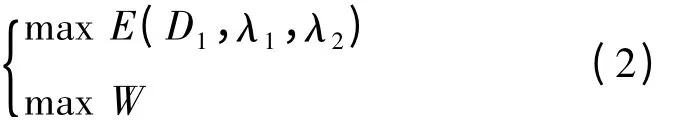
3 模型的求解

由上文可知，該模型的求解是一個多目標規劃問題。為此，可采用約束法將其轉化為單目標規劃問題［5］。以物資供應鏈的利潤期望為主要目標，對保障能力設定一個期望值，滿足保障能力不低于期望值的條件下，使得物資供應鏈利潤期望達到最大，即

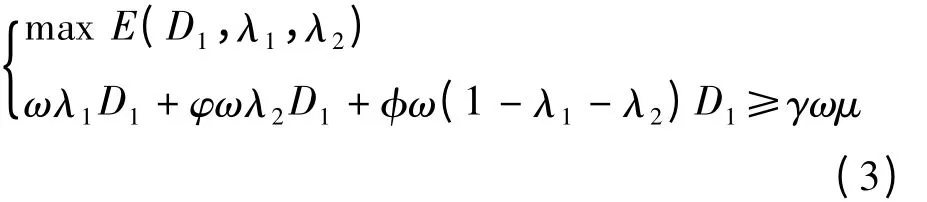
引入拉格朗日乘子η 和附加變量θ2，用拉格朗日乘數法構造拉格朗日函數［5］，由式(1)—(3)可得

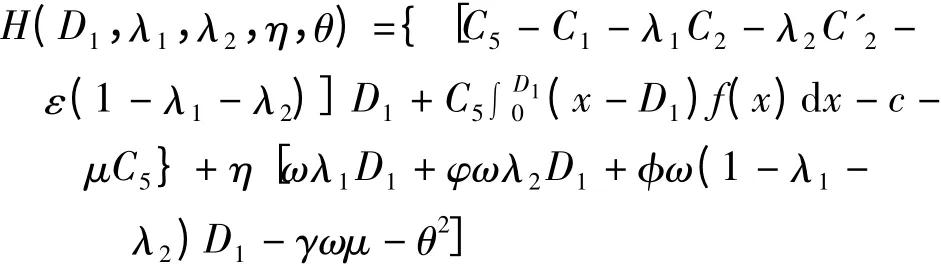
根據拉格朗日函數，極值點存在的必要條件:

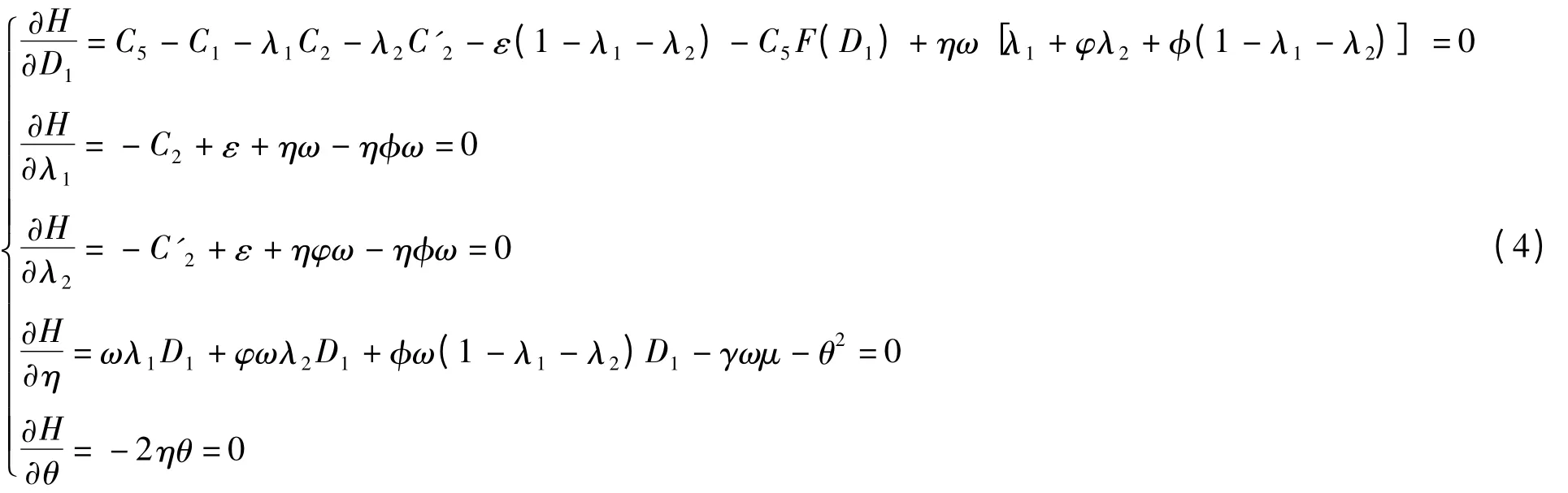
只要給定φ，φ 的取值和分布函數F表達式，便可解出D1、λ1、λ2和η 的取值。又由方程組(4)中第4 式可知，當滿足下列的條件時，該供應鏈的利潤期望值達到最大。

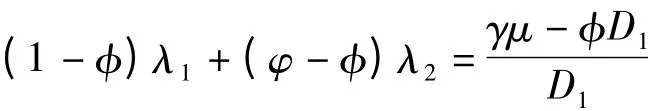
4 經濟補貼條件分析

4.1 從企業的角度分析

(1)對于合同企業，其利潤期望函數應該大于零，即Es=(D1，λ1，λ2)＞0，可得

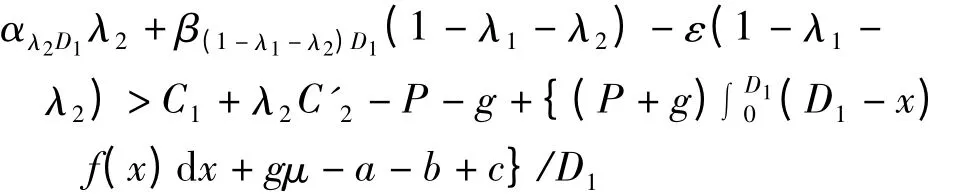
(2)對合同企業儲備總量(1-λ1)D1而言，采用合同企業實物、生產能力儲備物資儲備總成本應低于全部由合同企業進行實物儲備的總成本，即

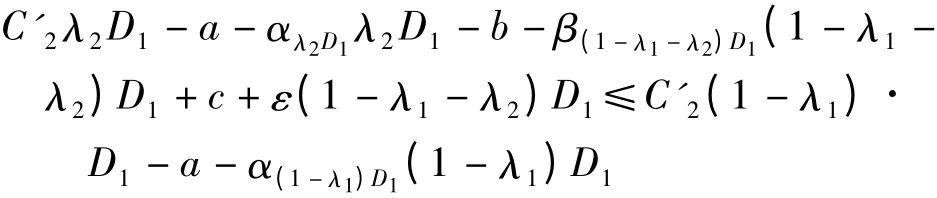
由此可得

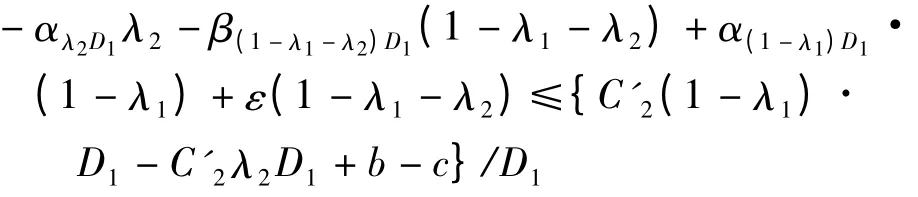
4.2 從軍隊的角度分析

(1)對于軍方而言，對儲備總量D1，采用軍隊與合同企業實物、生產能力儲備物資儲備總成本應低于全部由軍隊進行實物儲備的總成本，即

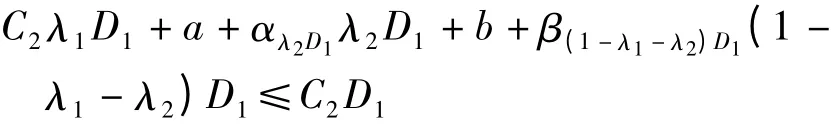
由此可得

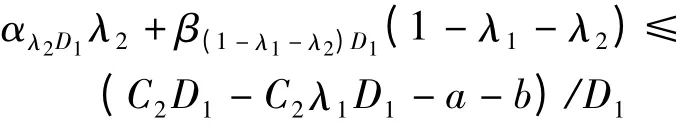
(2)軍隊對于合同企業實物儲備和合同企業生產能力儲備的補貼要小于只采用合同企業實物儲備的補貼，即

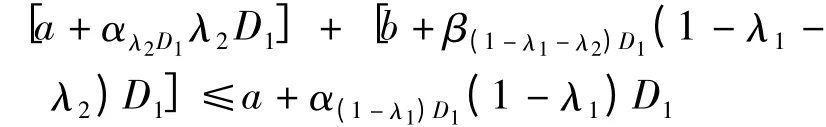
由此可得

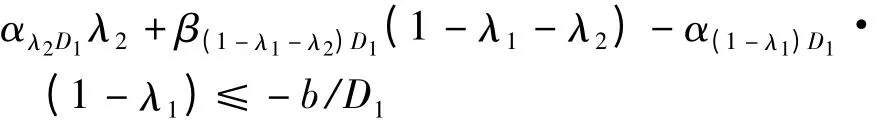
5 實例計算

假設某型號救災帳篷采取軍隊與合同企業實物、生產能力儲備的形式進行軍地聯儲。該型號每頂帳篷市場采購價格P為2 500 元，單位生產成本C1為1 600 元，軍隊單位庫存成本C2為200元/a，合同企業單位庫存成本C'2為120 元/a，合同企業保有生產能力儲備的固定成本c為10 000元，軍隊與合同企業實物儲備不能滿足需求時，采用其他方式獲取單位物資的成本C5為3 000 元。根據合同協議，合同企業物資儲備不足時單位懲罰成本g為1 000 元，軍隊每年向合同企業支付實物儲備固定補貼a為1.5 萬元，生產能力儲備固定補貼b為8 000 元，軍隊儲備單位物資的保障能力ω 為1，合同企業實物儲備單位物資的保障能力系數φω 為0.5，合同企業生產能力儲備單位物資的保障能力系數φω 為0.2，最低保障能力系數γω 為0.7。

為了使計算簡便，假設該型號帳篷的需求服從均勻分布X～U(40 000，120 000)，則由式(4)可得，該型號帳篷總儲備量D1為76 266 頂，軍隊實物儲備比例λ1為0.587 3，儲備數量約為44 791 頂，合同企業實物儲備比例λ2為0.214 9，儲備數量約為16 390 頂，合同企業生產能力儲備比例為0.197 8，儲備數量約為15 085 頂，即合同企業保有15 085 頂左右該型號帳篷的生產能力。此時，整個供應鏈利潤達到最大化，為-3.501 5億元，對需求的保障能力為56 002。

6 結 語

本文以軍地雙方圍繞物資儲備所發生的各種費用為主要依據，以供應鏈整體利潤最大化為目標，以保障能力為約束，構建了軍地物資聯儲經濟分析模型，通過該模型可以求解需求隨機的情況下的物資總儲備量以及軍地雙方的分攤比例，并可以通過補貼系數的調整實現供應鏈的協調，達到軍地共贏的目的。但在實際操作中，還需考慮軍地聯儲過程中的各種風險和由此產生的軍事、經濟成本代價，因而本模型也有一定的局限性，這也將是下一步需要研究的問題。

［1］ 金秀滿，曾勇，朱曉華. 戰備物資企業代儲的經濟性分析［J］.軍事經濟研究，2010(3):73.

［2］ 趙彥赟.軍民融合式戰備物資儲備發展策略研究［D］. 北京:后勤學院，2011:26-28.

［3］ 徐東.軍隊通用物資儲備社會化研究［R］. 北京:后勤指揮學院，2009.

［4］ 盛驟，謝式千，潘承毅. 概率論與數理統計［M］. 北京:高等教育出版社，2001:46-48.

［5］ 侯風波，張益池，張國勇，等.高等數學［M］.北京:高等教育出版社，2005.