一種基于證據理論的穩健設計方法

胡鈞銘， 楊燕紅， 魏發遠， 葛任偉

（1.西華大學交通與汽車學院，成都610039；2.中國工程物理研究院總體工程研究所，四川綿陽621900）

0 引言

工程實際中存在大量與材料理化特性、結構形狀參數、邊界條件和載荷等相關的不確定性，認識、量化和評估各種不確定性對于產品設計及綜合性能保證具有重要作用。不確定性是客觀事物聯系與發展過程中或然的、無序的、模糊的、近似的屬性。按照來源的不同可分為隨機不確定性與認知不確定性。隨機不確定性取決于變量的內在變異性，是客觀存在的，不能通過進一步的認知研究予以消除；認知不確定性主要由認識局限和知識缺乏所造成，隨著信息的增加可以予以降低［1］。

作為較早關注不確定性因素對產品性能影響的設計方法，穩健設計方法通過控制設計變量使產品對不確定性因素不敏感［2］。但是傳統穩健設計方法大多簡單地采用概率量化不確定性，這種簡單地認為所有不確定性均可采用概率理論進行量化，忽略了設計中存在的大量認知不確定性。1967 年，Dempster［3］提出了證據理論，隨后 G.Shafer［4］對其進一步研究和發展。研究表明，證據理論是對經典概率理論的一種擴展，能對隨機、模糊、區間等不確定性信息進行有效處理。近年來，證據理論已成為工程分析與優化方面的研究熱點［5-9］。本文提出一種基于證據理論的穩健設計方法，通過概率結構的證據化，建立起隨機與認知不確定性的統一分析框架，并基于根據響應證據結構所定義的均值與變差構建了穩健設計準則，實例研究演示和驗證了該方法的有效性。

1 證據理論基本原理

證據理論是建立在辨識框架上的不確定推理和決策理論，其理論基礎包括基本概率分配函數、信任函數、似然函數等以及Dempster證據合成規則等。

1.1 基本概率分配函數

設Θ是一個辨識框架，基本概率分配函數m是一個從集合2Θ到［0，1］的映射，A表示辨識框架Θ的任一子集，記作A?Θ，且滿足：

則將m（A）稱為事件A的基本概率分配值，它表示證據對事件A的信任程度。基本概率分配函數可根據已有數據或經驗構造。

1.2 信任函數與似然函數

信任函數Bel和似然函數Pl都是一個從集合2Θ到［0，1］的映射，若B表示辨識框架Θ的任一子集，則：

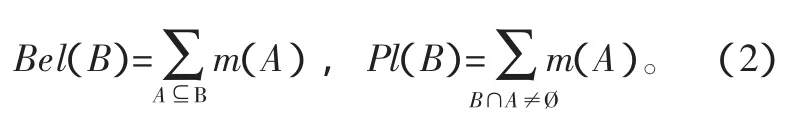
Bel（B）表示對B為真的信任程度，Pl（B）表示對B為非假的信任程度，且Pl（B）≥Bel（B），稱Bel（B）和Pl（B）分別為對B信任度的下限和上限，記為［Bel（B），Pl（B）］，它表示了對事件B的不確定區間。

1.3 Dempster合成規則

Dempster合成規則可以綜合不同專家或數據源的知識或數據，合并成一個概率分配函數，其定義如下：

對于?A?Θ，Θ 上的兩個質量函數m1、m2的Dempster合成規則為：

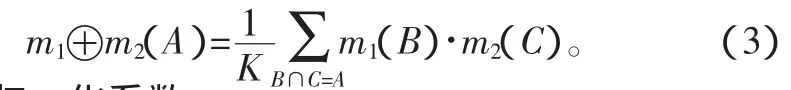
其中，K為歸一化系數：

式中K稱為歸一化因子，它反應了不同證據之間的沖突程度，K越小，則說明證據的沖突程度越大。Dempster合成規則在合成沖突證據時，會得出違反直覺的結論，對證據合成規則的改進見文獻［10］。

2 基于證據理論的穩健優化分析

穩健優化設計本質上是一個以不確定性量化為基礎的尋優過程，產品性能指標及其不確定性是尋優的依據。不確定性量化的結果（性能指標及其不確定性）與實際問題很好吻合，才能確保最終的優化結果具有實用價值。穩健優化設計中的不確定性分析主要包括：參數不確定性量化、不確定性傳播、穩健準則構建等。

有時候人們對醫院社會服務的認識存在誤解：認為它完全是為窮人服務的，主旨就是施財給錢。其實這并非是醫院社會服務宗旨，盡管在許多病例中，確實伴隨著貧困問題。

2.1 參數不確定性量化

參數不確定性量化，主要包括參數不確定性類型辨識和參數的不確定性表征。

2.1.1 不確定性類型辨識

參數的不確定性類型辨識是從認知的角度，依據所掌握的資料，確認參數的不確定性類型。對于給定的物理模型，系統響應則可被視為認知不確定性參數與隨機不確定性參數的函數，如式（5），其中y為系統響應，E為認知不確定性參數，A為隨機不確定性參數。

2.1.2 認知不確定性表征

證據理論能直觀表達專家的意見，利用系列帶有基本概率分配值的區間實現對認知不確定性參數的量化。專家基于各自的實際經驗，對認知不確定性參數進行估計，其形式為m（j）｝，j∈（1，2，…，M），其中 M 為區間總數，m（j）為第j個區間［，］的基本概率分配值。為了獲取較為準確的參數信息，可征求并利用合成規則整合不同專家的意見。

2.1.3 隨機不確定性表征

對于已知分布的隨機不確定性參數A，以A～N（μ，σ2）為例，將其近似截斷成［μ-ξσ，μ+ξσ］，然后離散截斷區間成N個子區間［，］，i∈（1，2，…，N），對于每一子區間，其基本概率分配值定義為

其中，f（x）是參數A的概率密度函數。顯然，隨機不確定參數子區間的基本概率分配值就是概率密度函數在指定區間的面積。

2.2 不確定性傳播

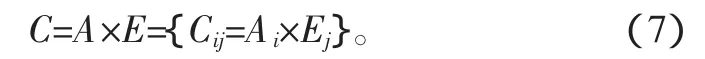
C表示所有參數的笛卡爾積，Cij是C的子集。當A和E相互獨立時，聯合基本概率分配值m（Cij）為：

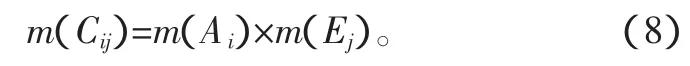
系統響應的不確定性是在參數聯合概率分配結構下，通過式（5）計算獲得響應的基本概率分配。即對于每一個Cij，計算響應的最小和最大值

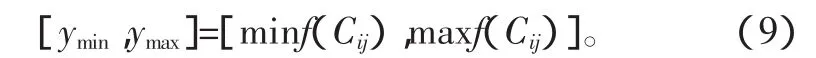
且m（［ymin，ymax］）=m（Cij）。顯然，聯合證據結構Cij的個數以及在其上響應極值的計算是決定證據理論分析計算時間的2個主要因素。

2.3 穩健設計準則

傳統基于概率論的穩健設計準則是在系統響應均值和方差的基礎上，通過在最小化響應波動的同時，盡可能減小均值與設計目標間的距離來實現的［11］。類比于概率論的均值和方差，提出了區間證據結構的均值和變差，以此作為評價響應穩健性的指標。

2 .3.1 區間證據結構的均值和變差

基于證據理論的不確定性傳播，獲得的系統響應是區間證據結構。為表征響應的集中和分散程度，定義區間證據結構的均值與變差。

2.3.2 穩健尋優流程

穩健設計根據產品性能需求的不同將設計分為望大、望小和望目三種［11］。基于響應區間證據結構均值與變差，分別構建了三類穩健設計準則。

望大/望小：max/min Ey+βDy，

望目：min （Ey-y0）2+β（Dy）2。

其中β為權值系數，在望大特性中可取為負值，即采用極大化最小值原則；在望小特性設計中可取為正值，即采用極小化最大值原則；在望目特性中，y0為設計目標值，綜合采用極小化均值與目標值間距離以及變差的原則。

3 實例研究

在導彈、衛星等航天器中，支撐結構及安裝在其上的功能組件（安裝板+隔振器+功能組件）構成一類廣泛采用的典型結構系統。該類結構的動態響應是表征其環境適應能力的重要指標，歷來受到高度重視。但在計算機仿真分析中由于模型簡化不可避免地引入認知不確定性，導致仿真結果與實際嚴重不符，進而影響設計決策。

本節以該類系統動態響應（系統加速度傳遞函數的第一個峰值）為設計目標，演示和驗證所提出的方法。為提高證據分析計算效率，通過建立響應與設計參變量間的近似模型替代有限元模型，結合優化算法求解聯合證據結構上的極值，并運用遺傳算法開展尋優。

3.1 響應面原理

響應面法結合試驗設計技術與統計學原理，在優化區域內建立響應與影響因素間的關系。一個系統的響應y依賴于 p個輸入因子 x1，x2，…，xp，如果考慮響應與影響因素間的線性關系，并考慮因素的交互效應和二次效應，二階響應面模型可表達為：

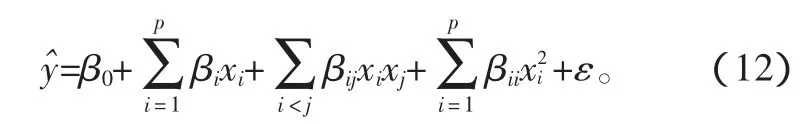
3.2 試驗設計與回歸

通過篩選確定了影響系統響應的因素：安裝板的厚度、安裝板的彈性模量、阻尼墊的高度、阻尼墊的半徑以及等效彈性模量（阻尼墊及連接結構有限元模型的等效彈性模量）。結構ANSYS有限元模型如圖1，安裝板采用單元Shell63，隔振器及連接結構采用單元Beam4，功能組件采用單元Solid45。選用5因素（1/2分式）正交旋轉組合設計，編碼水平如表1。

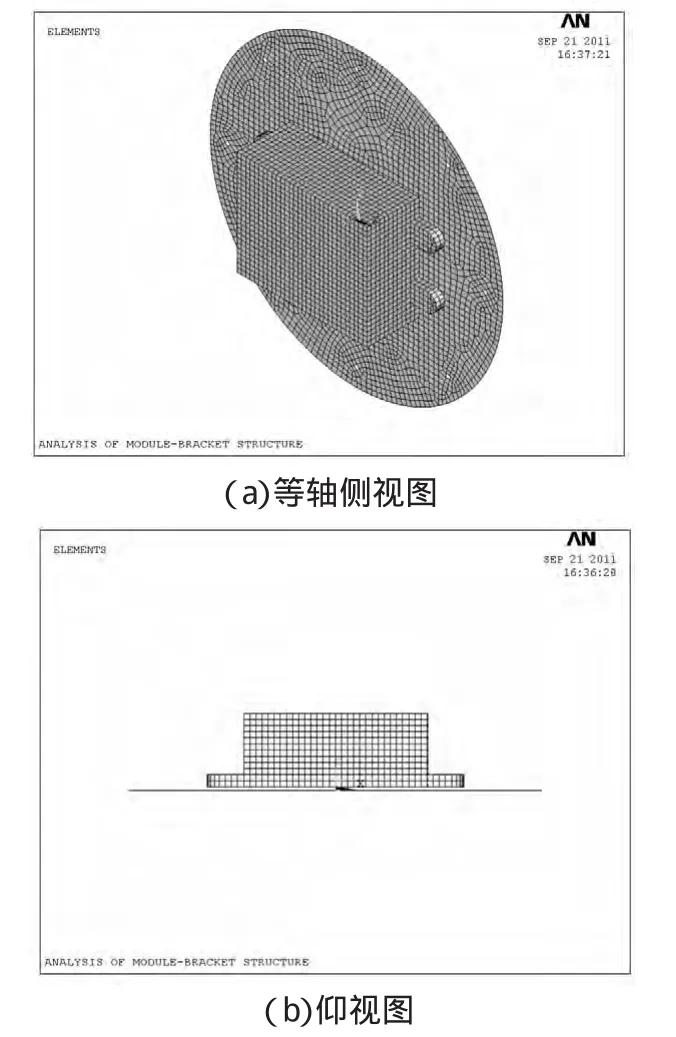
圖1 結構有限元模型

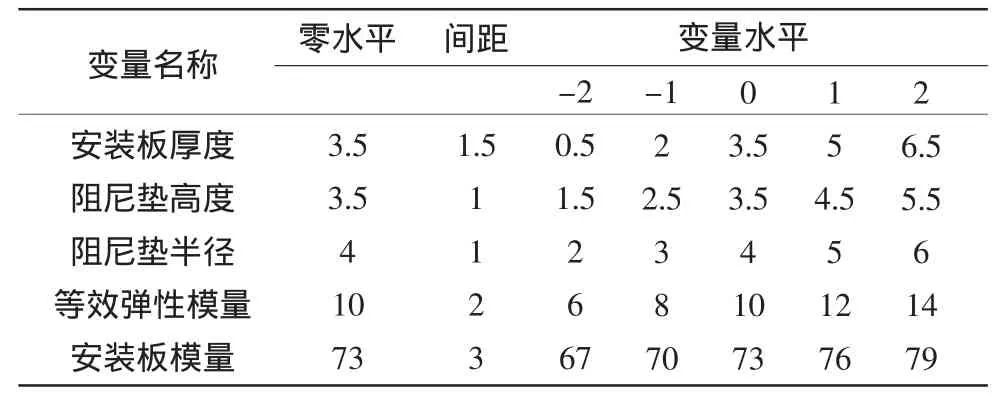
表1 變量水平信息表

對試驗數據表2進行擬合，并經回歸模型和回歸系數的顯著性檢驗，得到系統響應的回歸模型：

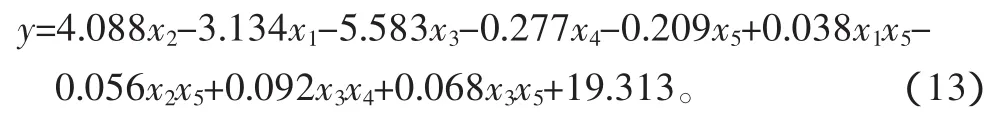
其中，x1、x2、x3、x4、x5分別代表安裝板的厚度、阻尼墊的高度、阻尼墊的半徑、等效彈性模量和安裝板的彈性模量，y為系統加速度傳函第一個峰值的對數值。

3.3 穩健優化

為使系統具有較強的環境適應能力和穩健性，因此系統加速度傳遞函數第一個峰值應盡可能小。優化目標采用望小特性，權值系數β取為1，綜合設計變量 x1、x2、x3的約束條件，優化模型如式（14）。由于認知不確定性參數造成目標函數不連續，不能直接使用梯度優化算法，而遺傳算法具有離散化、全局性、自適應等特點，結合遺傳算法的穩健優化計算流程如圖2所示。

考慮到實際加工過程的影響，假定設計變量x1、x2、x3均服從方差已知，均值未知的正態分布x1～N（μ1，0.01），x2～N（μ2，0.01），x3～N（μ3，0.01）；安裝板彈性模量 x5服從 N（73，1）的正態分布；專家1和專家2基于自身經驗給出的認知不確定性參數——等效彈性模量的信息及根據Dempster合成規則得到的整合信息見表3。

表2 試驗數據

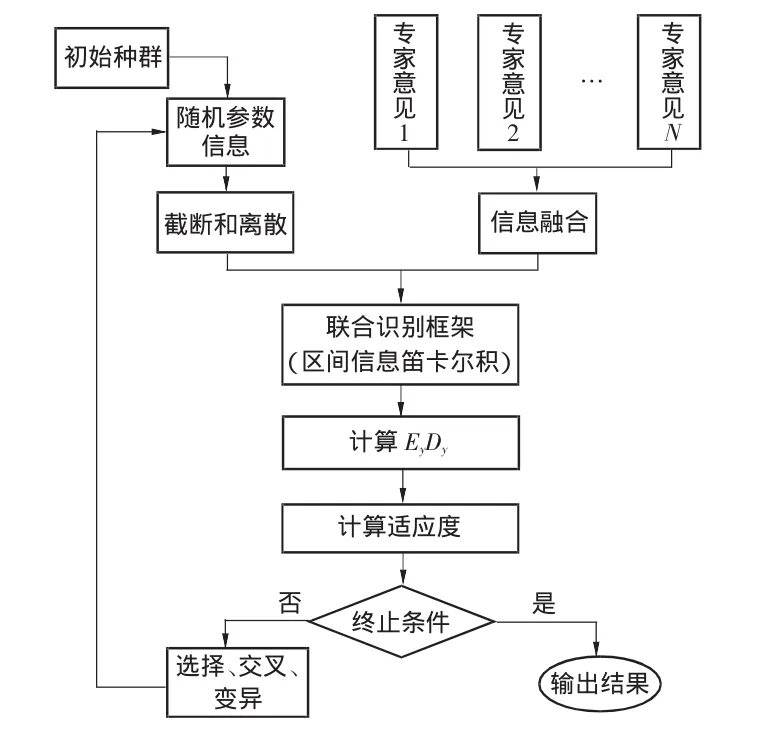
圖2 穩健優化計算流程

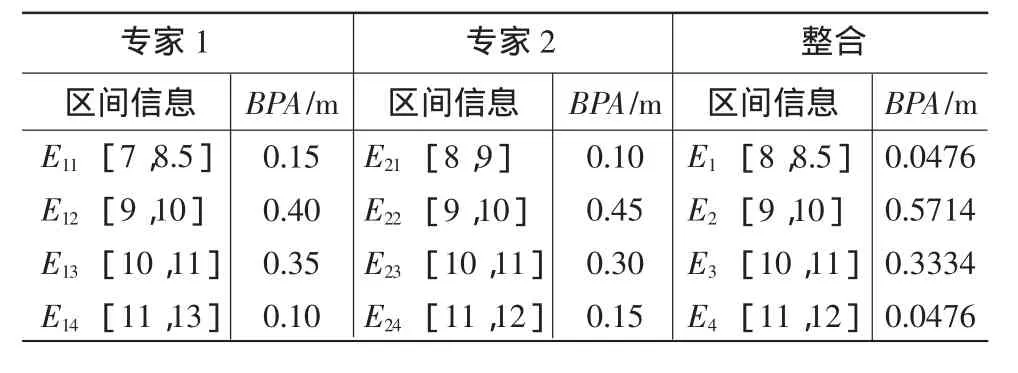
表3 等效彈性模量

采用MatlabR2009a優化工具箱（OptimizationToolbox）中的遺傳算法（genetic algorithm，GA）和fmincon函數，編制計算程序，得到計算結果x1=5，x2=3.25，x3=3。

4 結語

基于證據理論建立了認知與隨機不確定性統一分析框架，構建的穩健設計方法是一種廣義建模方法，為研究多類多源不確定性下的穩健設計問題提供了新思路。當設計模型中的不確定性變量和參數具有模糊性及其他未確知性時，通過轉化與融合，有望為穩健設計問題的研究提供新途徑、新方法。該方法比現有的穩健設計方法具有更強的處理不確定因素的能力，具有良好的工程應用前景。

［1］ Oberkampf W L，Helton J C，Joslyn C A，et al.Challenge problems：uncertainty in system response given uncertain parameters［J］.Reliability Engineering and System Safety，2004，85（2）：11-19.

［2］ GeorgH，SendhoffB.Robustoptimization-Acomprehensivesurvey［J］.Computer methods in applied mechanics and engineering，2007，196（33）：3190-3218.

［3］ Dempster A P.Upper and lower probabilities induced by a multivalued mapping ［J］.Annals of Mathematical Statistics，1967，38（2）：325-339.

［4］ Shafer G.A Mathematical Theory of Evidence［M］.Princeton，New Jersey：Princeton University Press，1976.

［5］ Bae H R，Grandhi R V，Canfield R A.Epistemic uncertainty quantification techniques including evidence theory for largescale structures ［J］.Computers&Structures，2004，82（13）：1101-1112.

［6］ Bae H R，Grandhi R V，Canfield R A.An approximation approach for uncertainty qualification using evidence theory［J］.Reliability Engineering&System Safety，2004，86（3）：215-225.

［7］ Agarwal H，Renaud J E，Preston E L，et al.Uncertainty quantification using evidence theory in multidisciplinary design optimization［J］.Reliability Engineering&System Safety，2004，85（1）：281-294.

［8］ Mourelatos Z P，Zhou Jun.A Design Optimization Method Using Evidence Theory［J］.Journal of Mechanical Design，2006，128（4）：901-908.

［9］ 郭惠昕，劉德順，胡冠昱，等.證據理論和區間分析相結合的可靠性優化設計方法［J］.機械工程學報，2008，44（12）：35-41.

［10］ Sentz K，Ferson S.Combination of Evidence in Dempster-Shafer Theory［R］//SAND2002-0835 Report，Albuquerque，New Mexico：Sandia National Laboratories，April2002.

［11］ 陳立周.穩健設計［M］.北京：機械工業出版社，1999.

［12］ 楊德.試驗設計與分析［M］.北京：中國農業出版社，2002.