動力機械非穩態過程的計算方法探索

趙燕娟， 張玉良

（1.衢州職業技術學院信息工程學院，浙江衢州324000；2.衢州學院機械工程學院，浙江衢州324000）

0 引言

對于動力機械而言，在非穩定工況情形下，如突然啟動、斷電停機、快速調節工況、快速變頻等，描述它性能的每一個參數在短時間內都將發生劇烈的變化。一般情形下，為了減少研究強度，通常僅對研究對象開展研究。若對單一研究對象進行內部流動計算，在指定邊界條件時，則必須知道轉速-時間曲線和流量-時間曲線，或者轉速-時間曲線和進出口壓力-時間曲線，而流量與壓力的變化又與管路系統特性密切相關。因此，要準確模擬出內部流場，需要通過實驗確定上述關系。在各式各樣的瞬態操作過程中，若存在轉速變化，則可通過基于用戶自定義函數功能來實現，內部旋轉區域作為一個整體旋轉。旋轉的轉子和靜止的定子在計算過程中存在相對運動，兩個區域通過滑移面聯接。對于瞬態過程中的非定常計算，每個時間步長計算一次交迭面；對于每個滑移面上的通量按照重疊面的面積比例計算得到，從而實現兩個區域的通量平衡。下面以一臺低比轉速離心泵的啟動過程為例，來探索數值模擬方法的可行性。

1 模型與方法

1.1 計算模型

本文中的計算模型與參考文獻中的計算模型完全相同［1］，模型泵額定流量 Q=6 m3/h，揚程 H=8 m，轉速 n=1450 r/min。計算域如圖1所示，計算域分為3部分，分別是進口段，葉輪旋轉區域和蝸殼靜止區域。葉輪旋轉區域作為一個整體旋轉。

1.2 計算方法

在快速啟動過程中，轉速-時間曲線基本上取決于動力源的啟動特性，并且該曲線關系近似滿足于指數關系［2］：

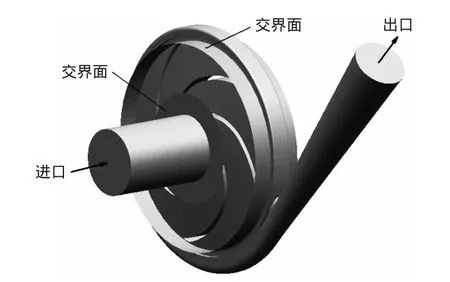
圖1 計算域

其中：nmax=1450 r/min；t0=0.15 s。轉速變化關系通過編寫用戶自定義函數施加到葉輪上。

已有文獻表明，流量變化近似滿足三次曲線形式。結合文獻［3］，在此處采用人為給定的形式，最大穩定流量設定為6 m3/h。假定的流量變化關系式如圖2中的流量曲線所示。根據質量守恒和幾何關系，可換算成速度，即在泵進口處采用速度進口邊界條件，在泵出口處采用自由出流條件。進口速度變化關系通過用戶自定義函數施加到泵進口處。湍流模型采用RNG k-ε湍流模型封閉時均雷諾方程。計算中的滑移網格技術已被廣泛用來計算穩定工況的性能預測［4］。瞬態項的離散采用一階隱式格式，壓力和速度的耦合采用SIMPLE算法實現，對流項采用一階迎風格式離散，擴散項采用中心差分格式離散。時間步長取0.0001 s，從靜止到達穩定轉速的時間約為1 s。在每個時間步長內取最大迭代次數為200次（實際上每個時間步長內迭代不到200次便可收斂），以保證在每個時間步長內都絕對收斂。收斂殘差為0.0001。計算介質為清水，密度 ρ=1000 kg/m3，動力黏度 μ=0.001 Pa·s，考慮重力影響，計算域網格總數為508792。

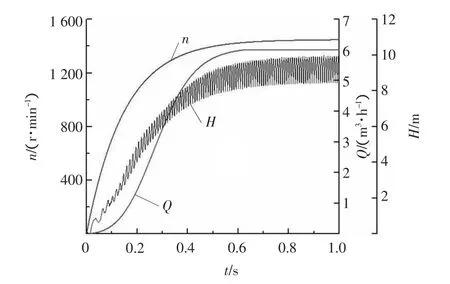
圖2 啟動過程中的揚程曲線

2 計算結果

圖2是計算得到的啟動過程離心泵揚程變化的時間歷程，其中轉速和流量曲線是外部指定的邊界條件與初始條件。可以看到，隨著轉速的增加，揚程波動值也隨之增加。最大波動值約為1.5 m，相對于設計揚程，可見波動時非常大的。

圖3是啟動過程中離心泵中截面上總壓變化的時間歷程。在0.04 s，由于轉速相對較低，故葉輪攪動水體做功，使得此時內部壓力場變化并不明顯。隨后隨著轉速的不斷上升，壓力梯度變得更為明顯。在任意時刻，壓力逐漸演變為從進口處的低壓轉變為葉輪出口處的高壓。并且中心壓力隨著轉速的增加而迅速降低。在0.6 s之后，葉輪部分壓力變化并不明顯，變化主要發生在蝸殼內部。從壓力場的演化趨勢與揚程外特性曲線的變化趨勢結合分析可知，兩者具有較好的對應關系。

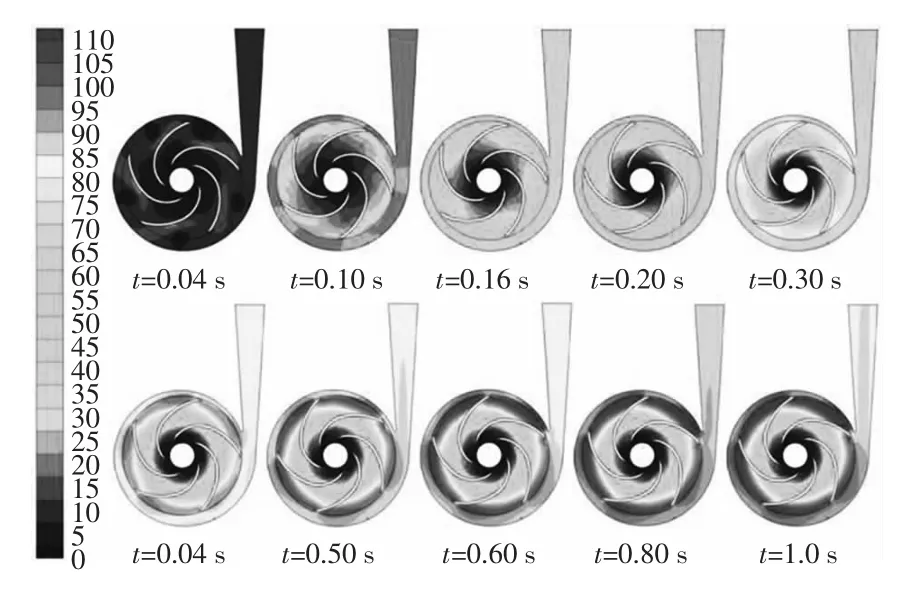
圖3 啟動過程中的總壓變化時間歷程（kPa）

3 結論

此算例采用滑移網格技術及用戶自定義函數相結合的方式對單一泵進行了啟動過程的三維非定常流動數值預測，從內流場和外特性的結果看，數值模擬方法是可行的。但由于轉速和流量的變化歷程是人為給定的，尤其是流量條件的給定更具不確定性，因此無法獲得準確可靠的非定常流場演化結果。根據前述分析，要獲得準確的流量、壓力曲線需要借助于實驗結果，才能數值模擬得到準確的內流場演化特征。

［1］ Zhang Yuliang，Li Yi，Cui Baoling，et al.Numerical simulation and analysis of solid-liquid two-phase flow in centrifugal pump［J］.Chinese Journal of Mechanical Engineering，2013，26（1）：53-60.

［2］ Tsukamoto H，Ohashi H.Transient characteristics of a centrifugal pump during startup period ［J］.ASME Journal of Fluids Engineering，1982，104（1）：6-13.

［3］ 平仕良,吳大轉,王樂勤.離心式水泵快速開啟過程的瞬態效應分析［J］.浙江大學學報：工學版，2007，41（5）：814-817.

［4］ 楊從新,巫發明,張玉良.基于滑移網格的垂直軸風力機非定常數值模擬［J］.農業機械學報，2009，40（6）：98-102.