一種交會時間固定的調相分析方法

孫國童，張柏楠，馬曉兵，黃 震

（中國空間技術研究院 載人航天總體部，北京 100094）

0 引言

我國載人航天工程已突破并掌握了交會對接技術，為后續空間交會對接任務奠定了良好的技術基礎。在后續交會對接任務中，目標飛行器不需配合調相，它與追蹤飛行器間的相位角完全由追蹤飛行器調相，要求追蹤飛行器具備更強的相位適應能力。但是，后續交會對接仍然在推進劑最省與交會飛行時間固定兩個約束條件下實施。在推進劑最省的約束下，調相軌道的半長軸只能在初始軌道與目標軌道之間選擇；在交會時間固定的情況下，追蹤飛行器無法通過在調相軌道上飛行足夠長的時間實現任意相位的調整。當追蹤飛行器在軌相位調整能力不足時，只能通過地面等待，即選擇在目標飛行器的緯度幅角落入相位調整能力范圍內的窗口發射追蹤飛行器入軌。因此，在目標飛行器不配 合調相的情況下完成空間交會對接任務，需要權衡地面等待時間與推進劑使用量的關系，合理規劃追蹤飛行器交會對接調相軌道控制策略，充分利用有限的推進劑與交會時間資源，最大限度地提升追蹤飛行器的調相能力、縮短地面等待時間。可見，提升追蹤飛行器的調相能力對標準化追蹤交會調相過程、增加發射窗口數量均具有重要意義。

本文研究在目標飛行器不配合調相的情況下追蹤飛行器的交會對接調相軌道設計問題，考慮推進劑最省和交會時間固定的約束條件，著重從以下兩個方面入手：一是定量分析不同地面等待時間對應的調相需求；二是充分利用推進劑和時間資源提升追蹤飛行器在軌調相能力。通過這兩個方面的工作，找到提升追蹤飛行器調相能力的有效途徑，為地面等待時間與推進劑分配量的權衡決策提供參考。

1 調相需求分析

假設目標飛行器不主動為交會對接作相位調整，需要追蹤飛行器通過地面等待并重新規劃遠距離導引段調相軌道策略，以適應不同共面時刻的目標飛行器的不同相位。顯然，采取“適應每個共面時刻的目標所處相位”與“通過地面等待方式適應某個共面時刻的目標相位”的策略對追蹤飛行器的調相能力需求是不同的，但從另一角度講，在一段時間內發射窗口的數量決定了對調相能力的需求。

為方便研究調相需求問題，首先定義發射窗口密度的概念：若在任意連續的n（n為正整數）天內存在一個共面時刻，追蹤飛行器的調相能力可以適應該時刻的目標相位，則發射窗口密度為1/n。

在發射窗口密度的基礎上，為了定量計算調相需求，下面提出一種適用于軌道高度不大于450 km的近圓交會對接軌道的調相需求計算方法。

假設目標飛行器在交會對接軌道，相鄰共面時刻相位變化量為δu，取值范圍為[0°, 180°]。u1為目標第1天共面時刻所處相位，取值范圍為[0°, 360°]，ui(i=1, 2,···,n)為第i天共面時刻目標所處的緯度幅角。αd為對追蹤飛行器的調相需求，如圖1所示。

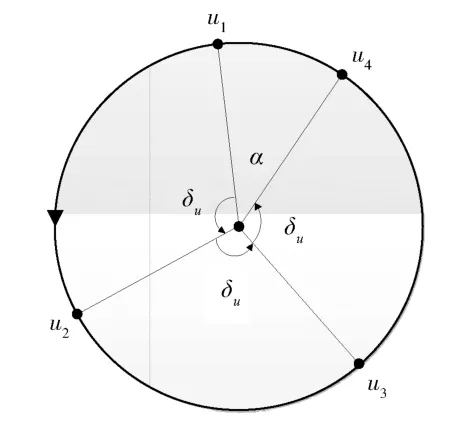
圖1 調相需求示意圖Fig.1 Illustration of phasing requirement

令α=mod(360,δu)，N=floor(360/δu)，則調相需求為

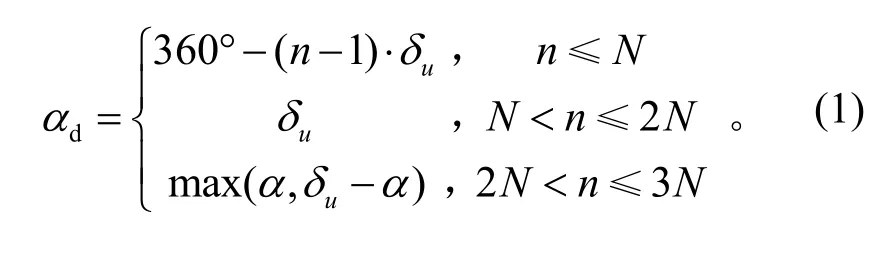
可以看出，調相需求主要與目標飛行器在交會對接軌道的相位回歸特性以及發射窗口密度相關：整數天相位回歸的交會對接軌道較為特殊，僅在發 射窗口密度定義中的n小于回歸天數N時，調相需求才隨發射窗口密度變大而提高；對于其他軌道，相同交會對接軌道條件下，發射窗口密度越大，調相需求越高。

2 調相能力分析

2.1 調相原理

調相基本原理根據開普勒第三定律[1]

式中：a為軌道半長軸；T為軌道周期；μ為地球引力常數。

追蹤飛行器通過在半長軸小于目標飛行器軌道半長軸的軌道上調相，獲取較大的角速度，經過Δt的調相時間后引起的相位差為其中，分別為追蹤 飛行器、目標飛行器的平均角速度。

在推進劑最省原則下，將調相能力（δΔθ）定義為追蹤飛行器與目標飛行器可實現交會對接的相位差區間的長度，即

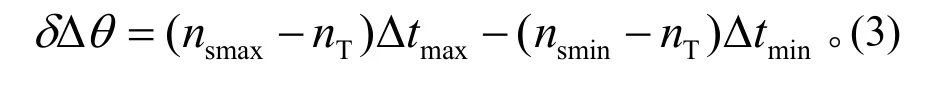
2.2 調相策略

在推進劑最省原則下，采用的特征點變軌調相策略[2-5]：

1）第N1圈遠地點施加跡向沖量ΔⅠt1，調整近地點高度；

2）第N2圈近地點施加跡向沖量ΔⅠt2，調整遠地點高度；

3）第N3圈遠地點施加跡向沖量ΔⅠt3，調整偏心率，進行軌道圓化。

2.3 誤差因素影響分析

1）初始入軌誤差

對調相產生影響的初始入軌誤差主要來自3個因素：

① 半長軸誤差ea

半長軸誤差將導致軌道平均角速度誤差，對相位角的影響將持續至第N1圈變軌前，經過Δt時間的累積，引起的相位角差異為[6]

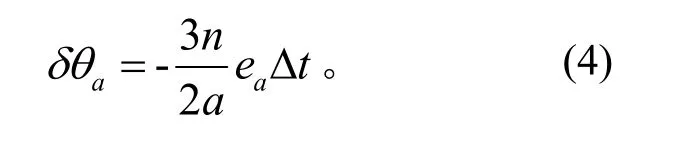
② 入軌時間誤差et

入軌時間誤差直接影響兩飛行器間相位差的初始值，對相位角的影響不隨時間累積，引起的相位角差異為δθt=nTet。

③ 入軌緯度幅角誤差eu

入軌緯度幅角誤差直接影響兩飛行器間相位差的初始值，引起的相位角差為eu。

在追蹤飛行器調相能力范圍內，上述3 種初始入軌誤差對遠距離導引段的終端影響非常小[7]；初始入軌誤差的影響主要發生在調相能力接近上下限的情況下。因此，提高初始入軌精度可以直接提升追蹤飛行器調相能力。

2）軌控誤差ev

考慮軌道機動誤差的值（均方差）為機動沖量大小的線性函數：ev=c1ΔⅠt+c2，其中c1為表征控制延遲的常數項，c2為表征加速度計測量精度的常數項，ΔⅠt為機動沖量沿跡向的分量，則因軌道機動誤差引起的相位角差為[6]

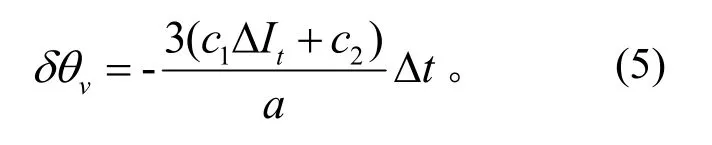
軌控誤差對遠距離導引終端的影響主要來自于最后一次軌道控制[7]；縮短最后一次軌道控制與遠距離導引終端的時間間隔，可以降低軌控誤差的影響。

3 調相能力提升途徑分析

由上述的調相原理分析可知，對于所采用的N個軌道周期的特征點變軌調相策略，追蹤飛行器的調相能力可描述為

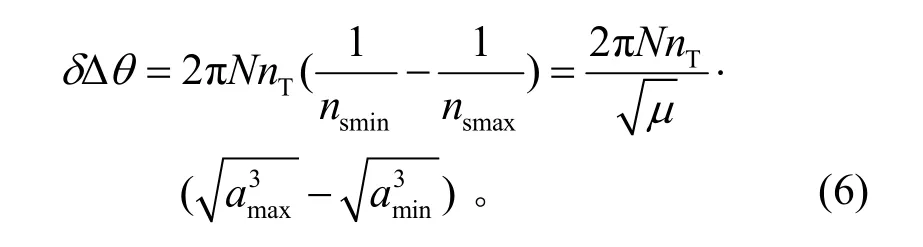
由式(6)可知，提升追蹤飛行器調相能力的途徑有兩條：

1）增加調相軌道圈數N；

2）擴大追蹤飛行器調相軌道半長軸變化范圍。

3.1 增加調相軌道圈數（時間）

遠距離導引策略中調相軌道的圈數決定了調相時間長短。因遠距離導引段總圈數固定，受地面測量確定飛行器軌道（測定軌）能力約束，測定軌占用圈數越多，用于調相的軌道圈數越少。

通過壓縮第一次軌控前、組合修正軌控前和遠距離導引段終點前的測定軌時間，可至少提供額外的3 圈調相軌道。

增加調相軌道圈數即增加了調相時間，可在不額外增加推進劑消耗的情況下，顯著提高調相能力，建議作為優先考慮的技術途徑。

3.2 擴大半長軸變化范圍

角速度差取決于調相軌道與交會對接軌道半長軸之差。追蹤飛行器利用遠距離導引段第一次變軌，調整自身軌道與交會對接軌道半長軸之差，實現對角速度差的調整，調整范圍受制于推進劑約束和初始軌道遠地點高度約束。

在推進劑最省原則下，式(6)中amax受運載能力和交會對接軌道高度限制，為常值。擴大半長軸范圍主要考慮如何減小amin。

1）根據目標相位調整追蹤飛行器初始入軌遠地點高度

初始入軌遠地點高度為定值，限制了amin的變化范圍，從而導致追蹤飛行器調相能力受限。

在推進劑分配量允許的范圍內，根據目標飛行器相位，降低初始入軌遠地點高度，減小amin的值，可實現調相能力的提升。

2）推進劑分配

為調相軌道提升所分配的推進劑越多，則初始入軌遠地點高度下調范圍越大，式(6)中amin取值越小，對應的相位調整范圍越大。

4 算例分析

以傾角56°、高度405 km 的3 天回歸軌道為例，對不同發射窗口密度下對應的調相需求進行仿真計算。顯然，每天都有發射窗口對調相能力的需求為360°，其他發射窗口密度下在(405±10) km 的軌道高度范圍內的調相需求如圖2所示。

在目標飛行器交會對接軌道標稱高度±10 km范圍內對追蹤飛行器調相需求的滿足情況進行了仿真計算，將誤差因素對調相的影響等效為調相需求，圖3為調相需求滿足情況。其中“原方案”指未采取提升途徑的調相方案；“途徑1”指采取壓縮測定軌時間以增加調相圈數的方案；“途徑1+途徑2”指采取文中兩種提升途徑后的方案。

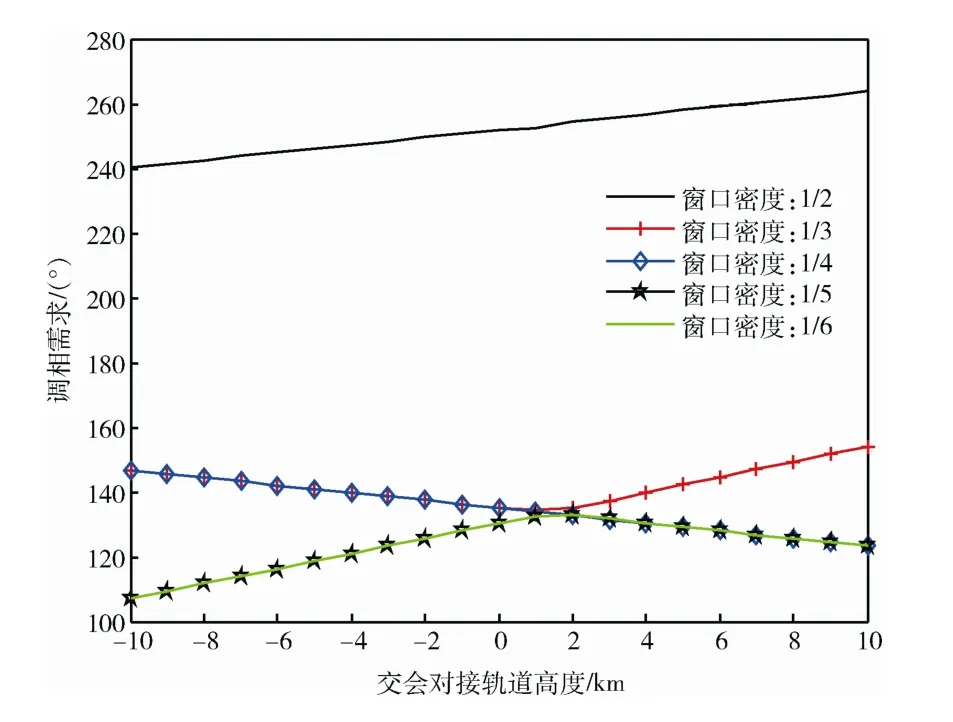
圖2 不同發射窗口密度下的調相需求Fig.2 Phasing requirement for various launch window densities

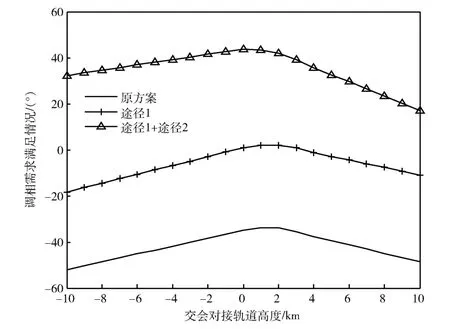
圖3 調相需求滿足情況Fig.3 Match condition for phasing requirement

由圖3可見，采取兩種提升途徑后，追蹤飛行器調相能力可以滿足發射窗口密度為1/3 的調相需求。僅采取“途徑1”時，調相能力與調相軌道圈數呈正比例關系，與理論分析結論一致；同時采取途徑1、2 后，在標稱高度±10 km 范圍內均能滿足調相需求，但在交會對接軌道高度超過運載能力時，用于下調amin的推進劑量減小，導致調相能力降低。

5 結束語

通過本文提出的調相需求與能力匹配分析方法，得到了發射窗口密度、交會對接軌道高度和調相策略的關系。調相能力提升途徑分析表明，能夠利用追蹤飛行器有限的推進劑資源，有效提高交會對接時間固定的在軌調相能力。后續需繼續深入分析增加調相時間、擴大半長軸調整范圍兩條技術途徑在工程實施中的可行性。

（References）

[1]劉林.航天器軌道理論[M].北京∶國防工業出版社, 2000∶37

[2]唐國金, 羅亞中, 張進.空間交會對接任務規劃[M]．北京∶科學出版社, 2008∶162

[3]張進.空間交會遠程導引變軌任務規劃[D].長沙∶國防科學技術大學, 2008

[4]羅亞中.空間最優交會路徑規劃策略研究[D].長沙∶國防科學技術大學, 2007

[5]Prussing J E, Chiu J H.Optimal multiple impulse time fixed rendezvous between circular orbits[J].Journal of Guidance Control and Dynamics, 1986, 9(1)∶17-22

[6]張進, 黃海兵, 王為, 等.空間交會目標航天器相位調整策略[J].中國空間科學技術, 2011, 31(1)∶33-41 Zhang Jin, Huang Haibing, Wang Wei, et al.Target spacecraft phasing strategy in orbital rendezvous[J].Chinese Space Science and Technology, 2011, 31(1)∶33-41

[7]湯溢, 王翔.航天器交會遠距離導引段誤差敏感度研究[J].航天器工程, 2010, 19(3)∶40-44 Tang Yi, Wang Xiang.Research on error sensitivity of spacecraft rendezvous phasing[J].Spacecraft Engineering, 2010, 19(3)∶40-44