一種三次多項式湍黏性底邊界層的流場分布
紀艷菊 , 劉淑波 齊 震
(1.中國科學院 海洋研究所, 山東 青島 266071; 2.中國科學院大學, 北京 100049; 3.中國石油大學(華東)理學院, 山東 青島 266580; 4.河北省地礦局第四水文工程地質大隊 滄州市海洋環境監測站, 河北 滄州061000)
湍流底邊界層的流場結構對于海洋工程研究具有十分重要的意義和理論價值, 比如泥沙的侵蝕,懸浮沉積過程[1-2]、湍流混合[3]、能量耗散[4]及Ekman抽吸[5]。迄今為止雖然有很多文獻從不同角度(如理論上和實驗上)研究了底邊界層的動力特征[6-13], 但是精確地描述復雜湍流底邊界層的動力機制卻十分困難。實際海洋中, 有很多因素影響底邊界層的動力系統, 如垂向渦黏性的分布、底部粗糙度、底邊界層上部流場的分布和Coriolis力等。其中垂直渦黏性的分布是一個十分重要的參數, 對它適當且準確地描述可以更好地預測和模擬湍流底邊界層的動力結構。
為了更加準確地理解邊界層的動力特征, 垂直渦黏性的各種假設被廣泛地提出[9-21]。眾所周知, 垂直渦黏性是底邊界層高度的函數。例如, 由長度混合假設知, 渦黏性υ1是底邊界層高度的線性函數υ1=kzu*, 其中k是 Karman常數(k≈0.4),z是底邊界層的垂直高度(原點在底邊界層的底部, 向上為正),u*=(τ/ρ)1/2是底摩擦速度,ρ是流體的密度,τ是底剪應力。利用線性參數模式, Weatherly等[9]推導出了海洋傾斜底邊界層的速度解析解; Cushman-Roisin等[5]利用該渦黏性研究了深海洋的底部Ekman抽吸; Zou[10]在該模式的基礎上, 同時考慮了湍流消耗和擴散效應, 得到了湍流底邊界層的速度解析解。另外, Ostendorf[12]和 Prandle[13]利用該線性模式分別研究了考慮地球旋轉的湍流底邊界層和邊界條件為無應力的潮流底邊界層。然而, 在這2個研究中, 由于分別考慮了地球的旋轉和底邊界層上表面應力的消失, 渦黏性的分布需要進一步修正。為了解決這個難題, 各種不同的渦黏性模式被提出。Beach等[14]提出了線性-指數形式的渦黏性υ2,υ2=k1ku*ze xp(-k2z/d), 其中k1,k2為 2個常系數,d是底邊界層的有效高度。通過該渦黏性, Hsu等[15]預測的湍流底邊界層的速度剖面和實驗觀測結果一致, Absi[16]計算了細沙和粗泥沙懸浮液的濃度。另外,Myrhaug[17]利用了湍流渦黏度的二次形式υ3=ku*z(1 -z/d)描述了粗糙底邊界層的湍流運動。根據實驗數據, Nezu等[18]得到了該渦黏性的二次形式,并進一步揭示了底邊界層的速度分布。Perlin等[19-20]利用此渦黏性研究了底Ekman層的湍流、分層和速度分布; Shimizu[11]考慮了分層和地轉效應得到了湍流底邊界層的解析模式, 并且和已知的實驗結果擬合良好。李明悝等[21]通過分析不同水深和潮流振幅情況下, 得到了一個潮致垂直混合渦動黏性系數υT的擬合公式υT=L(1 -z)2z2, 其中L為常數, 與潮流振幅和底混合層厚度有關, 在該參數化方案下, 模擬的海洋溫度三維結構和實際觀測基本吻合。
為了對問題進一步探討, 在本文研究中, 我們提出了三次多項式形式的渦黏性υ=az2(1 -z/d),其中a是常數(與摩擦速度u*與有效高度d有關),得到了湍流底邊界層的速度的解析解, 并進——步得出底邊界層內其他的動力參數的解析形式。在數學方法上, 湍流底邊界層的流場分布用超幾何函數表示[22]。超幾何函數在函數的展開和量子力學的問題中有很多的應用[23-24], 在湍流底邊界層的動力系統問題中卻很少被用到。本文在一個新的湍黏性分布下, 對方程進行適當的變量代換, 最終化簡為超幾何方程, 利用超幾何方程的基本解—超幾何函數來表示湍流底邊界層的動力結構。在文章最后利用數值結果討論了底邊界層的動力結構受一些參數的影響情況, 為研究底邊界層動力結構選用合適的渦黏性的形式提供了借鑒和參考。
1 底邊界層的控制方程和解析解
假定湍流底邊界層內的流體充分混合, 即密度均勻, 同時邊界層底部粗糙平坦。因此湍流底邊界層的運動基本方程可以簡化為Navier-Stokes (N-S)方程:
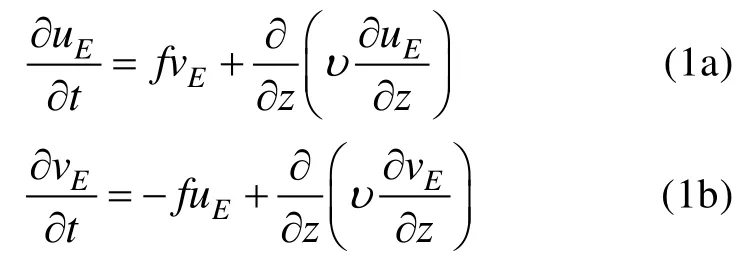
其中f= 2 Ω s inφ是Coriolis參數(本文中假設為正常數), Ω和φ分別是地球自轉角速度和地理緯度,t是時間,z是垂直高度(指向上為正的, 零點在底邊界層的底部, 見圖1)。υ=az2(1 -αz)為動力渦黏性,其中a是常數(與摩擦速度u*和底邊界層的有效高度d有關),α=1/d。uE和vE分別為x,y方向的虧損速度(Ekman速度), 它們是z和t的函數。而uI和vI為底邊界層上部x,y方向的速度分量(即底邊界層的總速度u,v分別為u=uI+uE和v=vI+vE)。
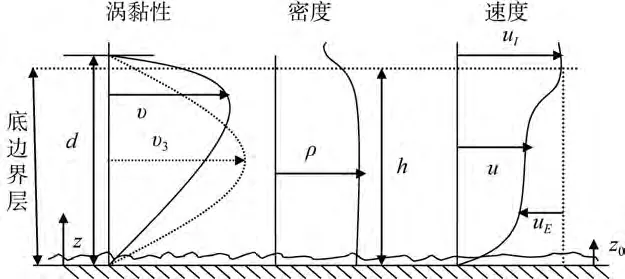
圖1 底邊界層示意圖Fig.1 Bottom boundary layer sketch
方程(1a)和方程(1b)的頂部邊界為無應力條件:
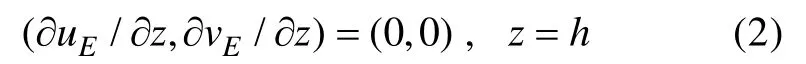
其中h為邊界層的厚度。
底邊界層的底部邊界為無滑移條件:
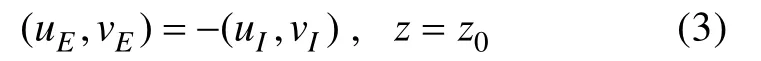
其中z0為底粗糙度, 本文假定為正常數。
底邊界層的上方由海洋潮汐力所產生的內部流場為:
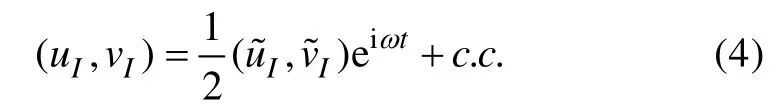
其中ω為內部流的角頻率,u~I和v~I為內部流速的復振幅且為常值,c.c.為復共軛。控制方程(1a)、(1b)在邊界條件(2)和(3)下, 得到了底邊界層速度的解析解。引入兩個新的變量F1=vE-iuE和F2=vE+iuE,帶入方程(1)得:
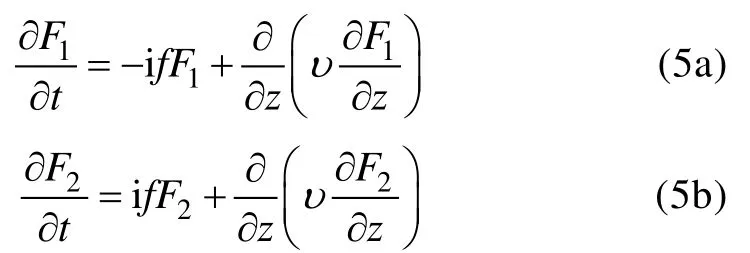
令F1=ρ1(z) eiωt,F2=ρ2(z) eiωt, 其中ρ1和ρ2分別是
z的兩個不同的函數, 方程(5)可簡化為:
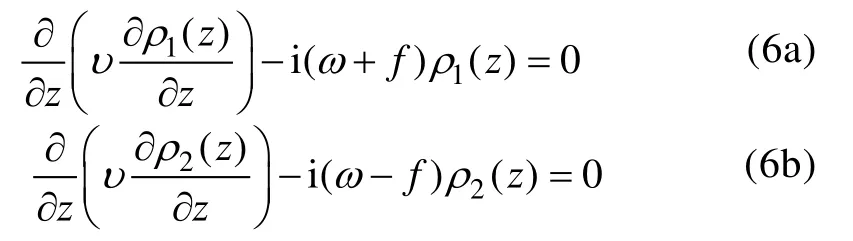
令ρ(z) =rpV(r),r=αz, 其中V是r的函數,p是復
1常數, 將上式代入(6a)。為進一步化簡方程的需要,令p2+p- i (ω+f)/α= 0 , 使得方程(6a)可化為超幾何方程[22]:
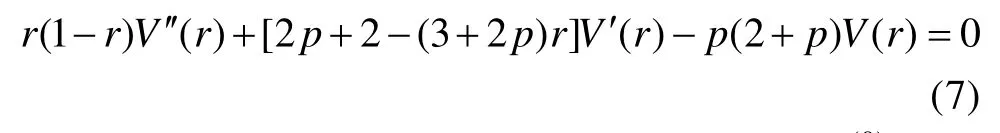
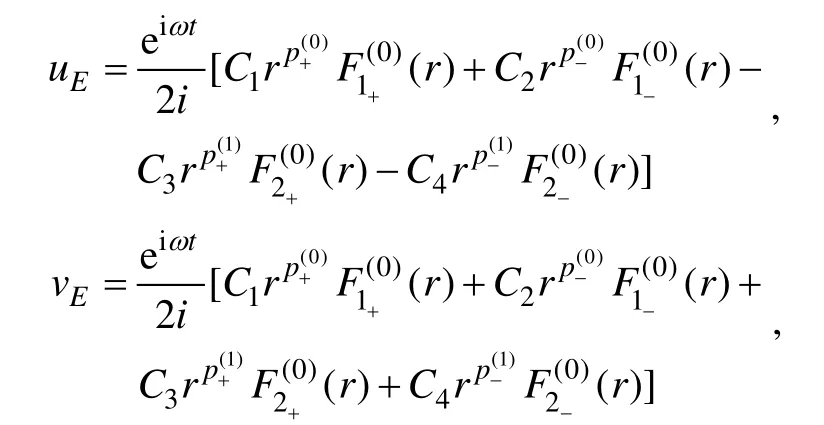
其中C1、C2、C3和C4是待定系數, 可由邊界條件(2)和(3)確定。則方程(1a)、方程(1b)的解為
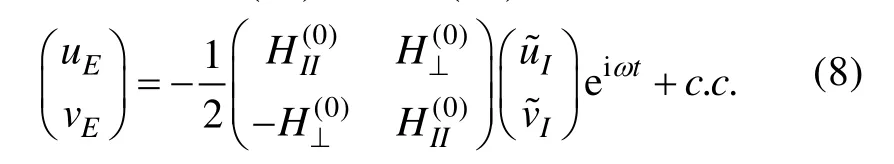
其中

2 底邊界層的動力參數
2.1 剪應力
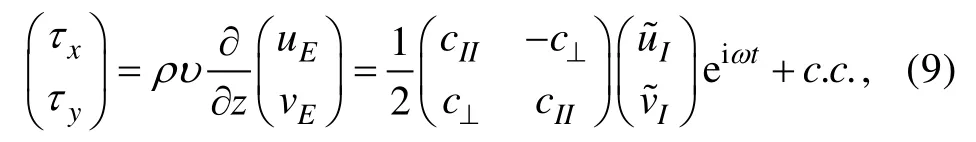
其中cII和c⊥為復線性摩擦系數,
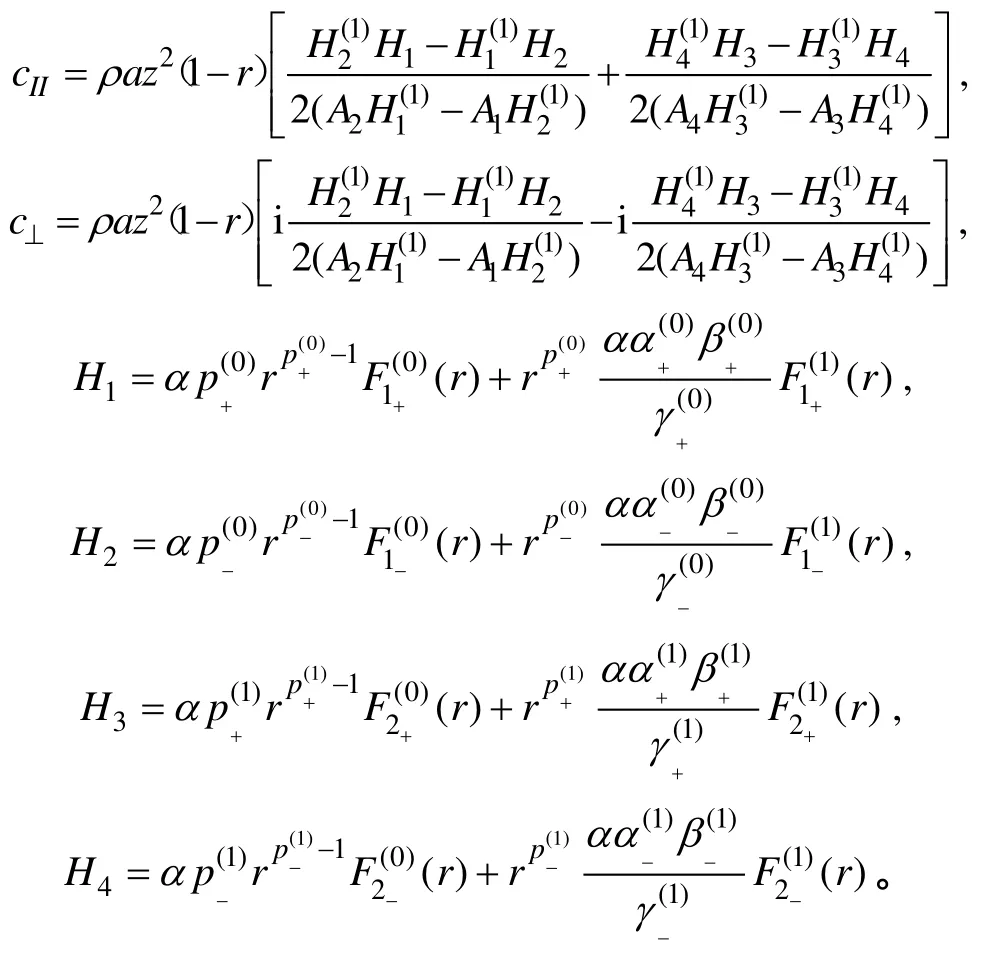
2.2 Ekman傳輸
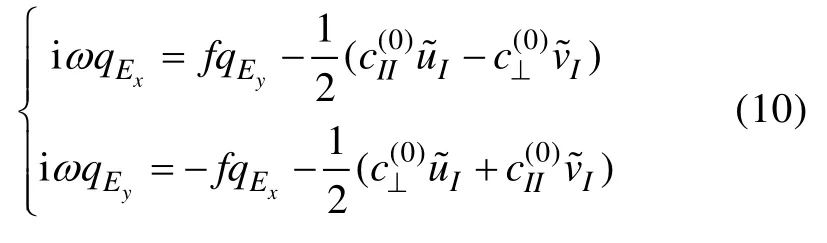
其中

進一步解得
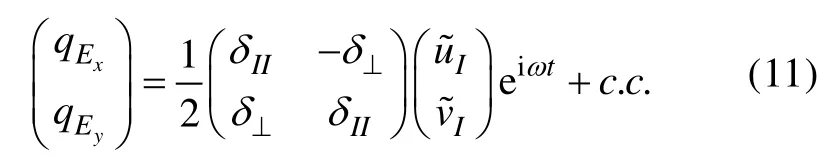
2.3 Ekman抽吸
假設流體為不可壓縮的, Ekman抽吸可由對三維 連 續 方 程 ?u/ ?x+ ?v/ ?y+ ?w/ ?z= 0 兩 端 分 別 從z=z0到z=h積分并結合公式(11)得到

其中wh表示z=h時, 底邊界層的垂向速度,wz0表示z=z0時, 底邊界層的垂向速度,wE表示Ekman抽吸,在伸展和壓縮海洋內部流方面起重要作用。
2.4 底邊界層近底部速度和剪應力
接近底邊界層的底部, 有極限(α=z/d→ 0 )和rp≈ 0 , 并利用超幾何函數的性質,[22]F(α,β,γ, 0 ) ≈ 1 , 利用邊界層速度公式(8), 我們得到底邊界層的近底部速度剖面,
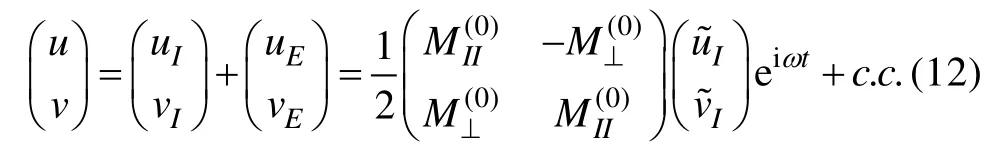
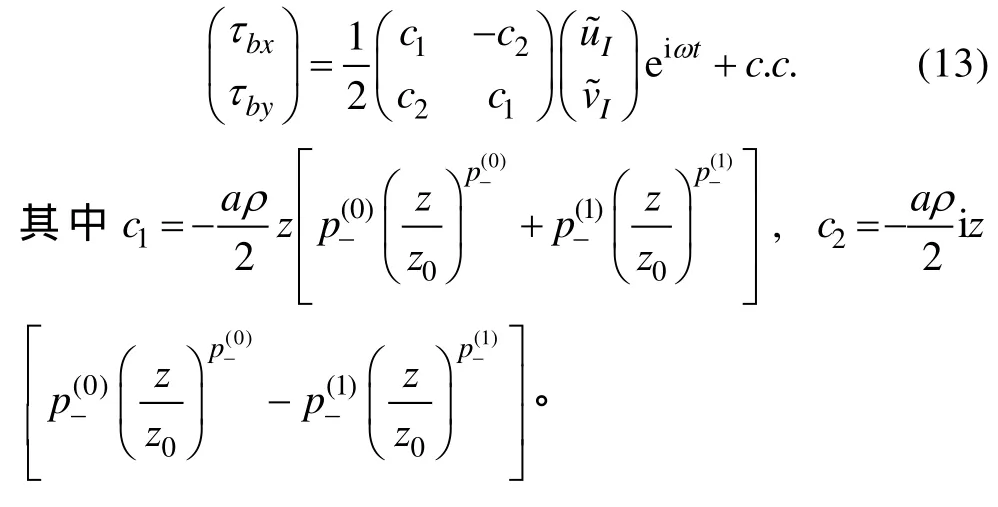
3 數值分析
作為動力特征分析, 在這部分, 我們假設一個單一內部流(uI,vI) = ( 0,1)VI, 其中VI為實常數, 表示速度的大小。在不考慮地轉效應的情況下, 分別討論了平均流的角頻率和底邊界層頂部粗糙度Δ =1 -h/d(圖1)對速度的影響情況(圖2和圖3)。在考慮了地轉效應情況下, 分別討論了參數S=ω/f和相位角ωt對底邊界層速度的影響情況(圖4~圖6), 以及參數S=ω/f對底邊界層剪應力的影響(圖7), 更加清晰地理解底邊界層內的動力結構。
在t=0s,f=0 rad/s,a=0.1 m/s, (uI,vI) = ( 1,0)VI和VI=1 m/s的情況下, 圖2給出了不同的平均流角頻率對應的無量綱的總速度剖面(u,v) = (uI+uE,vI+vE)的分布。從圖2可以看出總速度的大小|(u,v)|與平均角頻率有很大的關系。在底邊界層的同一高度上,隨著平均角頻率的增大而增大, 在角頻率為ω= 1.2× 1 0-4rad/s時, 總速度最大, 但是總速度的變化梯度越來越小; 對每個平均流的角頻率, 在接近邊界層的頂部時, 總速度達到在一個固定值, 在靠近邊界層底部, 總速度迅速減小為0。圖3給出了不同 Δ =1-h/d對應的總速度分布(=0.1、0.3和0.7)。在底邊界層的同一深度, 總速度的大小隨著Δ的增加越來越大, 但是影響不明顯。特別是在底邊界層近底部, 速度剖面對Δ幾乎不敏感。
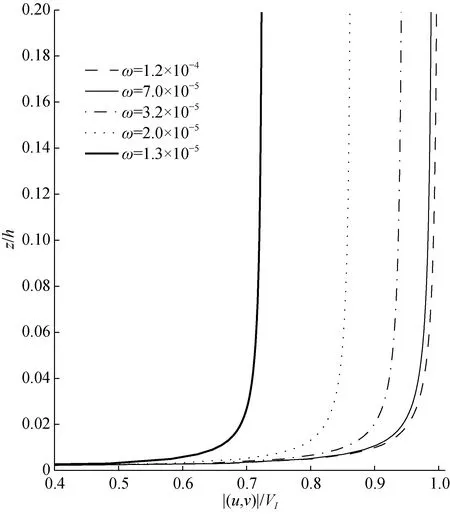
圖2 不同的角頻率ω下的速度剖面Fig.2 Velocity profile with different angular frequency ω
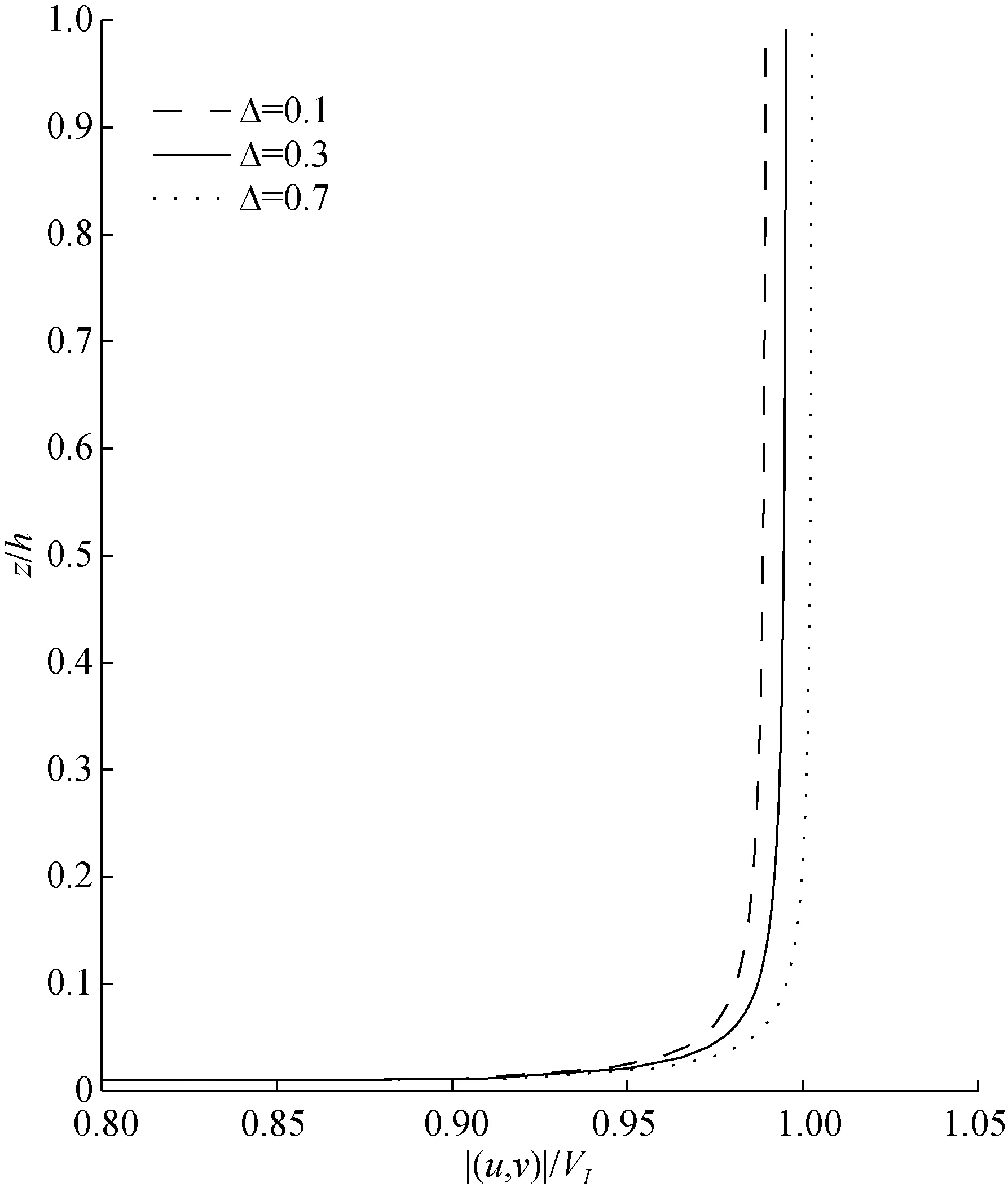
圖3 不同的Δ下的速度剖面Fig.3 Velocity profile with different Δ

圖4 不同S下的總速度的大小■(u, v)■(a)和相位arg[(u, v)](b)Fig.4 Velocity magnitude ■(u, v)■(a)and phase arg[(u, v)](b) with different parameters S , respectively
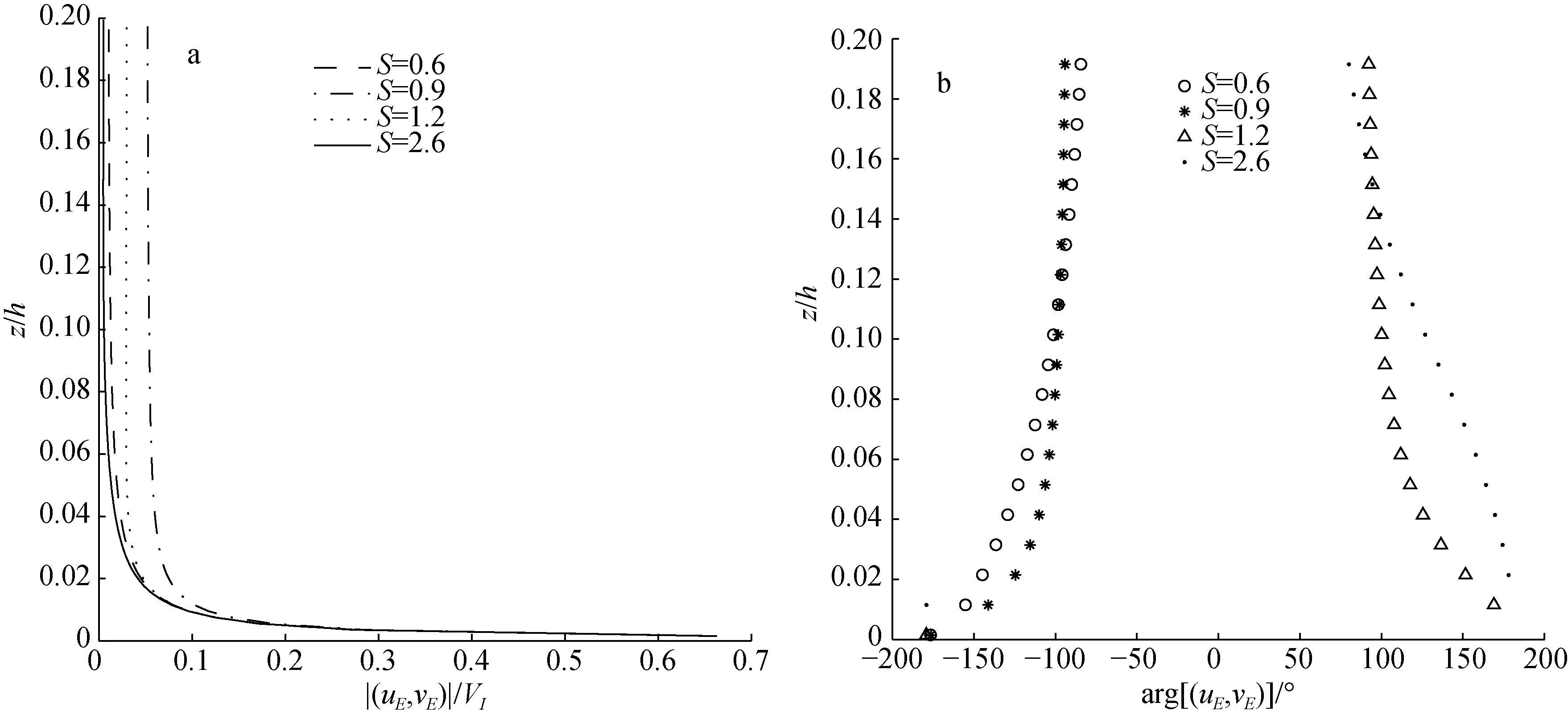
圖5 在不同S下的虧損速度的大小■(uE, vE)■(a)和相位arg[(uE, vE)](b)Fig.5 Velocity defect magnitude■(uE, vE)■(a)and phase arg[(uE, vE)](b)with different parameters S
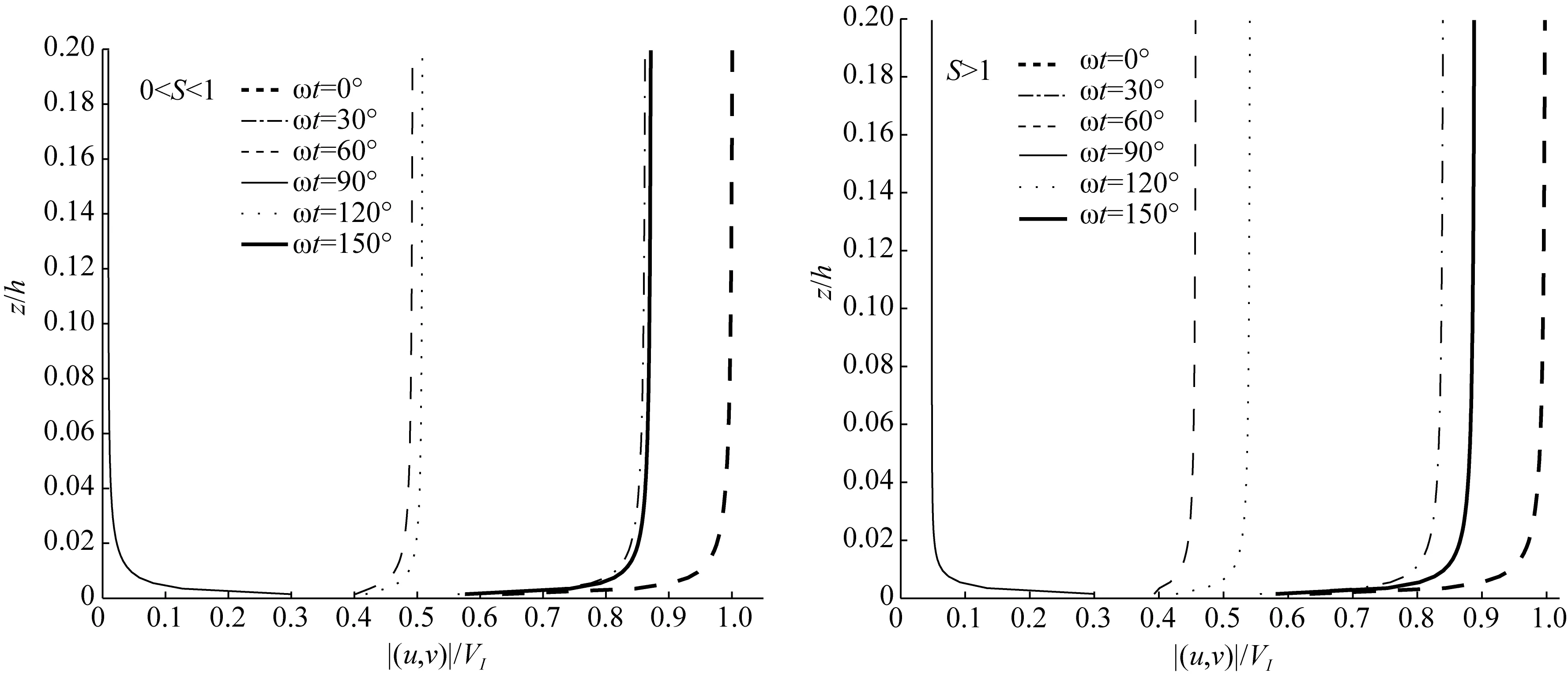
圖6 不同相位角tω下的總速度大小■(u, v)■的分布Fig.6 Velocity magnitude profile ■(u, v)■ with different phases tω
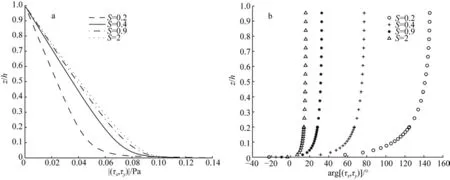
圖7 不同的S對應的剪應力的大小|(τx , τy ) | (a)和相位arg[(u, v)](b)Fig.7 The shear stress magnitude |(τx , τy ) | (a) and phase arg[(u, v)](b) with different S
在ω=7.27×10-5rad/s,t=0 s,a=0.01 m/s,(uI,vI)= ( 1,0)VI和VI=1 m/s的情況下, 圖4給出了在不同的S對應的總速度大小(a)和相位(b)分布(S=0.6、0.9、1.2和2.6)。從圖4(a)中可以看出, 速度的大小隨著S的變化很小, 特別是在邊界層的頂部和底部幾乎沒有變化。圖4(b)可以看出, 速度的偏轉角受到地球的自轉影響明顯, 當 0
在ω=7.27×10-5rad/s,a=0.1 m/s, (uI,vI)=(1,0)VI和VI=1 m/s的情況下, 圖6描述了在不同的相位角ωt(ωt=0°、30°、60°、90°、120°和150°)對應的總速度剖面的分布。在邊界層內, 當0
在ω=7.27×10-5rad/s,a=0.01 m/s, (uI,vI)=(1,0)VI和VI=1 m/s的情況下, 圖7給出了在不同S對應的底邊界層的剪應力大小(a)和相位(b)的分布情況。從圖中可以看出, 底邊界層的剪應力隨著高度的減小而增大, 最大值約為 0.14 Pa; 在底邊界層的相同高度, 剪應力的大小和相位隨著S的增加而減小,在底邊界層的底部, 相位約為–25°, 在底邊界層的頂部, 最大剪應力的相位約為150°。
4 討論
通過假定底邊界層的渦黏性的三次多項式形式,在簡化的N-S方程的基礎上, 通過變量代換, 利用超幾何方程的性質, 求得了粗糙底邊界層的速度的解析解。并進一步得到了底邊界層的其他的動力參數,如速度分布, 剪應力, Ekman傳輸, Ekman抽吸及近底部的速度和剪應力, 并且在該渦黏性模式下得到的近底部的速度非一般的對數形式。利用數值結果分析, 首先在不考慮地轉的情況下, 底邊界層內的總速度隨著平均流的角頻率的增加而增加, 而對于底邊界層頂部粗糙度的變化卻不是很敏感。其次是考慮地轉的情況下, 討論了底邊界層內的總速度,虧損速度及其底剪應力的變化, 由于地轉因素, 速度及其剪應力都有相位的變化。
本文所假設的渦黏性模式, 從理論上豐富了底邊界層渦黏性的形式, 須進一步通過實驗結果或觀測結果來驗證該模式的正確性, 這也是我們下一步要繼續研究的內容。另外, 能否通過進一步修改, 找到更接近觀測結果的渦黏性形式, 需要通過更多的實測資料來驗證。
[1]Gloor M, Wüest A, Münnich M.Benthic boundary mixing and resuspension induced by internal seiches [J].Hydrobiologia, 1994, 284: 59-68.
[2]曹祖德, 王桂芬.波浪掀沙、潮流輸沙的數值模擬[J].海洋學報: 中文版, 1993, 15(1): 107-118.
[3]魏皓, 趙亮, 劉廣山, 等.淺海底邊界動力過程與物質交換研究[J].地球科學進展, 2006, 21(11):1180-1184.
[4]劉志宇, 魏皓.黃海潮流底邊界層內湍動能耗散率與底應力的估計[J].自然科學進展, 2007, 17(3):362-369.
[5]Cushman-Roisin B, Mala?i? V.Bottom ekman pumping with stress-dependent eddy viscosity[J].Journal of Physical Oceanography, 1997, 27(9): 1967-1975.
[6]Sleath J F A.Turbulent oscillatory flow over rough beds[J].Journal of Fluid Mechanics, 1987, 182: 369-409.
[7]Jensen B L, Sumer B M, Freds?e J.Turbulent oscillatory boundary layers at high Reynolds numbers[J].Journal of Fluid Mechanics, 1989, 206: 265-297.
[8]Hanert E, Deleersnijder E, Blaise S, et al.Capturing the Bottom boundary layer in finite element ocean models[J].Ocean Modelling, 2007, 17(2): 153-162.
[9]Weatherly G L, Martin P J.On the structure and dynamics of the oceanic bottom boundary layer [J].Journal of Physical Oceanography, 1978, 8: 557-570.
[10]Zou Q P.An analytical model of wave Bottom boundary layers incorporating turbulent relaxation and diffusion effects[J].Journal of Physical Oceanography,2002, 32(9): 2441-2456.
[11]Shimizu K.An analytical model of capped turbulent oscillatory Bottom boundary layers[J].Journal of Geophysical Research-oceans, 2010, 115(C0): 3011.
[12]Ostendorf D W.The rotary Bottom boundary layer[J].Journal of Geophysical Research-Ocean, 1984, 89(10):410-461.
[13]Prandle D.The vertical structure of tidal currents [J].GeophysIcal.and Astrophysical Fluid Dynamics, 1982,22: 29-49.
[14]Beach R A, Sternberg R W.Suspended sediment transport in the surf zone: response to cross-shore infragravity motion [J].Marine Geology, 1988, 80:61-79.
[15]Hsu T W, Jan C D.Calibration of Businger-Arya type of eddy viscosity model's parameters[J].Journal of Waterway Port Coastal and Ocean Engineering-Asce,1998, 124(5): 281-284.
[16]Absi R.Concentration profiles for fine and coarse sediments suspended by waves over ripples: An analytical study with the 1-DV gradient diffusion model[J].Advances in Water Resources, 2010, 33(4): 411-418.
[17]Myrhaug D.On a theoretical model of rough turbulent wave boundary layers[J].Ocean Engineering, 1982,9(6): 547-565.
[18]Nezu I, Rodi W.Open-channel flow measurements with a laser Doppler anemometer[J].Journal of Hydraulic Engineering, 1986, 112(5): 335-355.
[19]Perlin A, Moum J N, Klymak J M, et al.A modified law-of-the-wall applied to oceanic Bottom boundary layers[J].Journal of Geophysical Research-oceans,2005, 110(C10): 110.
[20]Perlin A, Moum J N, Klymak J M, et al.Organization of stratification, turbulence, and veering in Bottom Ekman layers[J].Journal of Geophysical Researchoceans, 2007, 112(C5): 112.
[21]李明悝, 侯一筠, 喬方利.潮致垂直渦動黏性系數的參數化[J].自然科學進展, 2006, 16(1): 55-60.
[22]Abramowitz M, Stegun I A.Handbook of Mathematical Functions.With Formulas, Graphs, and Mathematical Tables [M].Washington, DC: National Bureau of Standards, 1964: 555-566.
[23]厚宇德.超幾何函數在量子力學上的應用[J].哈爾濱商業大學學報: 自然科學版, 2002, 18(3): 334-335, 329.
[24]朱嘉麟.超幾何方程的解在函數展開中的應用[J].計算物理, 1988, 5(4): 455-465.

