胞孔構(gòu)型對(duì)金屬蜂窩動(dòng)態(tài)力學(xué)性能的影響機(jī)理＊

胡玲玲，蔣 玲

（中山大學(xué)工學(xué)院應(yīng)用力學(xué)與工程系，廣東 廣州510275）

蜂窩作為一種多胞材料，具有良好的能量吸收能力、較高的比強(qiáng)度和比剛度等性能，因此，將其做成輕質(zhì)結(jié)構(gòu)和能量吸收構(gòu)件在航空航天、汽車工業(yè)、交通運(yùn)輸?shù)阮I(lǐng)域有廣闊的應(yīng)用前景。作為吸能材料，蜂窩往往受到?jīng)_擊荷載的作用，因此對(duì)蜂窩動(dòng)態(tài)力學(xué)性能的研究已成為近年來(lái)的一個(gè)研究熱點(diǎn)。很多研究已表明，蜂窩的相對(duì)密度對(duì)其力學(xué)性能有重要的影響［1］，除此之外，胞孔的幾何構(gòu)型［2－3］、加載方式［4］和加載速度［5－6］等也會(huì)影響多胞材料的力學(xué)性能。研究胞孔構(gòu)型與蜂窩宏觀力學(xué)性能之間的關(guān)系對(duì)蜂窩材料的設(shè)計(jì)有重要意義。L.L.Hu等［6］和D.Ruan等［7］給出了正六角形蜂窩動(dòng)態(tài)承載力的表達(dá)式，并進(jìn)一步研究了胞壁夾角對(duì)六角形蜂窩動(dòng)態(tài)力學(xué)性能的影響［8－9］。X.M.Qiu等［3］給出了具有不同胞孔構(gòu)型的蜂窩的平臺(tái)應(yīng)力經(jīng)驗(yàn)公式。Y.Liu等［10］保持胞壁厚度與長(zhǎng)度之比不變，研究了三角形和四邊形胞孔蜂窩的承載力。另外，胡玲玲等［2］、張新春等［11］討論了胞孔構(gòu)型對(duì)蜂窩能量吸收性能的影響。這些研究重點(diǎn)分析了胞孔構(gòu)型在特定加載方式下對(duì)蜂窩力學(xué)性能的影響，對(duì)于具有同一種胞元的蜂窩，在不同加載方式下其表現(xiàn)出的力學(xué)性能也會(huì)不同［4］。以上這些研究是在控制胞壁長(zhǎng)度和厚度不變的情況下，對(duì)比具有不同胞孔構(gòu)型的蜂窩的力學(xué)性能。然而，對(duì)于不同胞孔構(gòu)型的蜂窩，其相對(duì)密度與胞孔尺寸間的關(guān)系是不同的，這將引入相對(duì)密度的影響。本文中，在控制相對(duì)密度和沖擊速度不變的情況下，通過(guò)研究7種金屬蜂窩的力學(xué)行為，剖析胞孔構(gòu)型對(duì)金屬蜂窩動(dòng)態(tài)力學(xué)性能影響的內(nèi)在機(jī)理，以期研究結(jié)果對(duì)蜂窩胞孔構(gòu)型的設(shè)計(jì)有一定的指導(dǎo)意義。

1 有限元模型

基于ANSYS－LSDYNA建立金屬蜂窩的有限元模型，將蜂窩材料放置在一個(gè)固定的剛性板上，在其上方受到另一剛性板以恒定速度v＝120m／s沿豎直方向的沖擊，如圖1所示。蜂窩的基體材料采用金屬鋁，假設(shè)為理想彈塑性材料，服從Mises屈服準(zhǔn)則，楊氏模量E＝69GPa，屈服應(yīng)力σys＝76MPa，密度ρs＝2 700kg／m3，泊松比υ＝0.3。剛性板選用鋼材，其楊氏模量為210GPa，密度為7 800kg／m3。胞壁選用Shell163殼單元，參照文獻(xiàn)［6，8，10］，每個(gè)胞壁在長(zhǎng)度方向劃分為16個(gè)單元，足以描述胞壁的變形和胞孔的坍塌過(guò)程。限制各節(jié)點(diǎn)的面外位移，以防止試件發(fā)生面外屈曲。

本文中涉及了7種胞孔構(gòu)型，分別為：規(guī)則排布三角形胞孔（T－R）、交錯(cuò)排布三角形胞孔（T－S）、規(guī)則排布正方形胞孔（S－R）、交錯(cuò)排布正方形胞孔（S－S）、x方向受壓的正六角形胞孔（H－X）、y方向受壓的正六角形胞孔（H－Y）和Kagome（K）排布胞孔，如圖2所示。這些蜂窩材料的相對(duì)密度均為0.1，模型尺寸均為58.5mm×70.2mm。

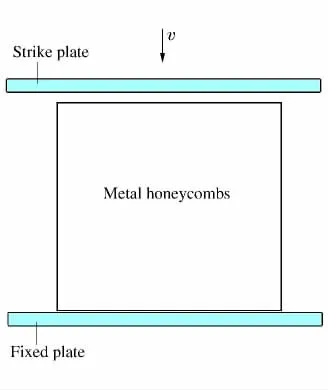
圖1 數(shù)值計(jì)算的有限元模型Fig.1 FEM model for simulations

圖2 蜂窩的胞孔構(gòu)型Fig.2 Various cell configurations of honeycombs

2 變形模式及蜂窩分類

各種蜂窩試件在宏觀應(yīng)變（即試件的壓縮變形量除以試件的原始高度）分別為0.52和0.78時(shí)的變形如圖3所示。由圖3（a）和（c）可知，對(duì)于具有規(guī)則排布三角形或四邊形胞孔的蜂窩材料（T－R和S－R蜂窩），胞孔從蜂窩的上下兩端向中間逐層壓垮密實(shí)，形成明確的局部化變形帶；而具有交錯(cuò)排布胞孔的蜂窩（T－S和S－S蜂窩），雖然在沖擊端形成密實(shí)帶，與此同時(shí)密實(shí)帶之外的胞孔也發(fā)生了較大變形，如圖3（b）和（d）所示。從圖2所示的胞孔構(gòu)型可以發(fā)現(xiàn)，對(duì)于具有交錯(cuò)排布胞孔的蜂窩，如圖2（b）和（d）所示，胞孔的某些端點(diǎn)正好位于相鄰一行胞的水平胞壁的中點(diǎn)，這將導(dǎo)致水平胞壁在上一行胞孔的坍塌過(guò)程中發(fā)生折彎，如圖3（b）和（d）所示，從而發(fā)生連鎖反應(yīng)，使變形遍及整個(gè)試件。而具有規(guī)則排布胞孔的蜂窩（T－R和S－R蜂窩）其胞孔排列是點(diǎn)對(duì)點(diǎn)、邊對(duì)邊的形式，如圖2（a）和（c）所示，胞孔坍塌以胞壁的受壓屈曲變形為主，對(duì)相鄰一行胞的影響較小，因而它們的變形會(huì)集中在有限的區(qū)域。

對(duì)于正六邊形蜂窩，無(wú)論是沿x方向加載還是沿y方向加載，蜂窩在變形過(guò)程中都沿沖擊端形成局部變形帶。沿x方向加載的蜂窩（H－X），其傾斜胞壁首先被上方的豎直胞壁壓為水平，進(jìn)而向下轉(zhuǎn)動(dòng)，如圖3（e）所示。沿y方向加載的蜂窩（H－Y），在變形過(guò)程中，胞壁繞在其端點(diǎn)所形成的塑性鉸轉(zhuǎn)動(dòng)，最終以波浪形方式緊密排列在一起，形成密實(shí)帶，如圖3（f）所示。

Kagome蜂窩作為一種特殊的組合模型，是由正三角形和正六邊形共同構(gòu)成。Kagome蜂窩的變形也是集中在上下兩端，如圖3（g）所示。

將蜂窩的坍塌胞孔放大后觀察（見(jiàn)圖3），可以發(fā)現(xiàn)胞孔的坍塌機(jī)制大致分為2種：一種主要由胞壁繞端點(diǎn)轉(zhuǎn)動(dòng)（胞壁基本保持直線），從而引起胞孔坍塌，如H－X和H－Y蜂窩；另一種主要由胞壁中間發(fā)生折彎，導(dǎo)致胞孔坍塌。對(duì)于前一種情況，胞壁在胞孔坍塌過(guò)程中僅繞端點(diǎn)轉(zhuǎn)動(dòng)，說(shuō)明該胞壁的受力以彎矩（應(yīng)力狀態(tài)為彎曲應(yīng)力）為主。對(duì)于后一種情況，如果折彎點(diǎn)處連接其他胞壁，該胞壁的折彎主要由其他胞壁施加的橫向荷載所致，此時(shí)該胞壁的受力也以彎矩為主，如T－S和S－S蜂窩；如折彎點(diǎn)處沒(méi)有連接其他胞壁，該胞壁的折彎是由其發(fā)生軸向受壓屈曲所致，說(shuō)明胞壁的受力以膜力（應(yīng)力狀態(tài)為膜應(yīng)力）為主，如T－R、S－R和 K蜂窩。

因此，根據(jù)胞壁所受的應(yīng)力狀態(tài)，將這些蜂窩分為彎曲主導(dǎo)蜂窩和膜力主導(dǎo)蜂窩2大類。彎曲主導(dǎo)蜂窩包括分別沿x方向和y方向加載的正六邊形蜂窩（H－X和H－Y）以及交錯(cuò)排布的三角形（T－S）和四邊形（S－S）蜂窩。規(guī)則排布的三角形（T－R）和四邊形（S－R）蜂窩以及Kagome蜂窩屬于膜力主導(dǎo)蜂窩。

圖3 蜂窩的變形模式Fig.3 Deformation modes of honeycombs

3 動(dòng)態(tài)承載力

圖4中給出了蜂窩在沖擊荷載下的應(yīng)力應(yīng)變（σ－ε）曲線。從圖4可以看出，相對(duì)于彎曲主導(dǎo)蜂窩，膜力主導(dǎo)蜂窩的平臺(tái)應(yīng)力波動(dòng)幅度較大。主要原因在于，膜力主導(dǎo)蜂窩的胞壁往往承受壓應(yīng)力，進(jìn)而發(fā)生屈曲，導(dǎo)致胞壁在屈曲瞬間承載力突然下降，從而在蜂窩的應(yīng)力應(yīng)變曲線上表現(xiàn)為較大幅度的波動(dòng)；而彎曲主導(dǎo)蜂窩的胞壁以受彎曲荷載為主，其應(yīng)力應(yīng)變曲線波動(dòng)幅度較小。

從圖4也可以看出，膜力主導(dǎo)蜂窩的平臺(tái)應(yīng)力高于彎曲主導(dǎo)蜂窩的平臺(tái)應(yīng)力。為了進(jìn)一步明確該結(jié)論，圖5中比較了這些蜂窩的動(dòng)態(tài)承載力σc，其中動(dòng)態(tài)承載力定義為蜂窩應(yīng)力應(yīng)變曲線在平臺(tái)階段應(yīng)力的平均值。一般來(lái)說(shuō)，高速?zèng)_擊下，慣性效應(yīng)對(duì)蜂窩的動(dòng)態(tài)承載力起重要作用，其影響與蜂窩的密度ρ和沖擊速度的平方v2成正比［6，12］。本文中所研究的這些蜂窩具有相同的密度和沖擊速度，因此圖5所示的各種蜂窩承載力之間的差別主要由胞孔的不同構(gòu)型引起，可見(jiàn)胞孔構(gòu)型確實(shí)對(duì)蜂窩的動(dòng)態(tài)承載力有明顯影響。Kagome蜂窩表現(xiàn)出最高的承載力，y方向加載的六角形蜂窩的承載力最低。胞孔規(guī)則排列的蜂窩（T－R和S－R）的承載力高于胞孔交錯(cuò)排列的蜂窩（T－S和S－S）。總的來(lái)說(shuō)，圖5表明胞孔的坍塌機(jī)制決定了膜力主導(dǎo)蜂窩比彎曲主導(dǎo)蜂窩具有更高的承載力。

圖4 蜂窩的應(yīng)力應(yīng)變曲線Fig.4 Stress－strain curves of honeycombs

圖5 蜂窩的動(dòng)態(tài)承載力Fig.5 Crushing strength of honeycombs

4 能量吸收性能

多孔材料常常被作為能量吸收構(gòu)件，圖6中給出了各種蜂窩所吸收的能量Ea隨應(yīng)變的變化曲線。從圖6可以看出，這些曲線明顯分成了2束，胞孔規(guī)則排布的三角形（T－R）和四邊形（S－R）蜂窩以及Kagome（K）蜂窩的曲線聚集為一束，表現(xiàn)出較高的能量吸收能力，其他幾種蜂窩的能量曲線較低。對(duì)照胞壁的應(yīng)力狀態(tài)，可以發(fā)現(xiàn)能量曲線的分束正好與蜂窩根據(jù)胞壁應(yīng)力狀態(tài)的分組相對(duì)應(yīng)，即膜力主導(dǎo)蜂窩比彎曲主導(dǎo)蜂窩具有更高的能量吸收能力。

圖6 蜂窩吸收的能量隨應(yīng)變的變化關(guān)系Fig.6 Energy absorbed by honeycombs varied with strain

圖7 蜂窩內(nèi)能的分?jǐn)?shù)隨應(yīng)變的變化關(guān)系Fig.7 Internal－energy fraction of honeycombs varied with strain

在沖擊過(guò)程中，蜂窩吸收的能量主要轉(zhuǎn)化為2大部分，即蜂窩的內(nèi)能和動(dòng)能，將兩者之和定義為總能。圖7中給出了各種蜂窩在變形過(guò)程中內(nèi)能占總能量的分?jǐn)?shù)γi。從圖7可以看出，內(nèi)能占總能量的分?jǐn)?shù)在受壓初期迅速增加，進(jìn)入平臺(tái)區(qū)后穩(wěn)定在某一值：彎曲主導(dǎo)蜂窩（T－S、S－S、H－X和H－Y）的內(nèi)能占總能量的分?jǐn)?shù)穩(wěn)定在0.6左右，而膜力主導(dǎo)蜂窩（T－R、S－R和Kagome）的保持在0.7左右。這說(shuō)明，蜂窩吸收的能量絕大多數(shù)轉(zhuǎn)化成了內(nèi)能，并且膜力主導(dǎo)蜂窩的內(nèi)能在其總能量中占的分?jǐn)?shù)更高。

為了進(jìn)一步剖析2組蜂窩在能量吸收能力方面的差別，圖8和圖9中分別給出了蜂窩的動(dòng)能Ek和內(nèi)能Ei隨應(yīng)變的變化過(guò)程。所有蜂窩在變形過(guò)程中動(dòng)能的變化較接近（見(jiàn)圖8），而它們的內(nèi)能曲線（見(jiàn)圖9）卻類似總能量曲線（見(jiàn)圖6）分成了上下2束，較高的一束為膜力主導(dǎo)蜂窩，較低的一束為彎曲主導(dǎo)蜂窩。這說(shuō)明，2組蜂窩吸收能量間的差別主要來(lái)自于不同的內(nèi)能，膜力主導(dǎo)蜂窩在變形過(guò)程中能耗散更多的內(nèi)能，這也是其具有較高承載力和能量吸收能力的原因。

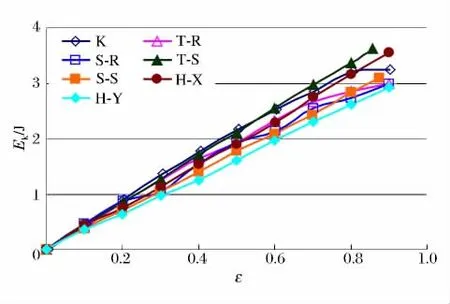
圖8 蜂窩動(dòng)能隨應(yīng)變的變化關(guān)系Fig.8 Kinetic energy of honeycombs varied with strain

圖9 蜂窩內(nèi)能隨應(yīng)變的變化關(guān)系Fig.9 Internal energy of honeycombs varied with strain

5 結(jié) 論

金屬蜂窩的胞孔構(gòu)型確實(shí)會(huì)對(duì)其動(dòng)態(tài)承載力和能量吸收能力產(chǎn)生影響，其主要原因在于不同的胞孔構(gòu)型決定了胞壁的受力狀態(tài)和坍塌機(jī)制不同。根據(jù)胞壁的應(yīng)力狀態(tài)可將蜂窩分為膜力主導(dǎo)蜂窩和彎曲主導(dǎo)蜂窩2大類。膜力主導(dǎo)蜂窩在壓潰過(guò)程中以胞壁的受壓屈曲為主，會(huì)出現(xiàn)荷載的突然下降，因而其應(yīng)力應(yīng)變曲線表現(xiàn)出較大幅度的波動(dòng)；彎曲主導(dǎo)蜂窩的胞壁以受彎曲荷載為主，其應(yīng)力應(yīng)變曲線波動(dòng)幅度較小。蜂窩吸收的能量大部分轉(zhuǎn)化為胞壁的內(nèi)能，并且膜力主導(dǎo)蜂窩的內(nèi)能在其總能量中占的分?jǐn)?shù)更高。2類蜂窩在變形過(guò)程中動(dòng)能的變化接近，膜力主導(dǎo)蜂窩比彎曲主導(dǎo)蜂窩具有更高的承載力和能量吸收能力，其主要原因在于膜力主導(dǎo)蜂窩在變形過(guò)程中能耗散更多的內(nèi)能。

對(duì)照胞孔構(gòu)型圖（圖2）可以發(fā)現(xiàn)，膜力主導(dǎo)蜂窩的胞孔構(gòu)型同時(shí)滿足以下2個(gè)條件：（1）每個(gè)胞孔頂點(diǎn)所連接的胞壁均成對(duì)出現(xiàn)，并且每對(duì)胞壁都位于同一條直線上；（2）這些胞壁在胞孔頂點(diǎn)上關(guān)于加載方向?qū)ΨQ。這2個(gè)條件保證了蜂窩胞壁在變形初期以受壓縮膜力為主，表現(xiàn)出較優(yōu)越的力學(xué)性能。這對(duì)蜂窩的工業(yè)應(yīng)用及其胞孔構(gòu)型設(shè)計(jì)有一定的指導(dǎo)意義。

［1］Gibson L J，Ashby M F.Cellular solids：Structure and properties［M］.2nd ed.Cambridge，UK：Cambridge University Press，1997：99－158.

［2］胡玲玲，陳依驪.三角形蜂窩在面內(nèi)沖擊荷載下的力學(xué)性能［J］.振動(dòng)與沖擊，2011，30（5）：226－229.Hu Ling－ling，Chen Yi－li.Mechanical properties of triangular honeycombs under in－plane impact loading［J］.Journal of Vibration and Shock，2011，30（5）：226－229.

［3］Qiu X M，Zhang J，Yu T X.Collapse of periodic planar lattices under uniaxial compression，part II：Dynamic crushing based on finite element simulation［J］.International Journal of Impact Engineering，2009，36（10／11）：1231－1241.

［4］Hu L L，Yu T X，Gao Z Y，et al.The inhomogeneous deformation of polycarbonate circular honeycombs under inplane compression［J］.International Journal of Mechanical Sciences，2008，50（7）：1224－1236.

［5］Zou Z，Reid S R，Tan P J，et al.Dynamic crushing of honeycombs and features of shock fronts［J］.International Journal of Impact Engineering，2009，36（1）：165－176.

［6］Hu L L，Yu T X.Dynamic crushing strength of hexagonal honeycombs［J］.International Journal of Impact Engineering，2010，37（5）：467－474.

［7］Ruan D，Lu G，Wang B，et al.In－plane dynamic crushing of honeycombs：A finite element study［J］.International Journal of Impact Engineering，2003，28（2）：161－182.

［8］胡玲玲，尤帆帆.鋁蜂窩的動(dòng)態(tài)力學(xué)性能及影響因素［J］.爆炸與沖擊，2012，32（1）：23－28.Hu Ling－ling，You Fan－fan.Dynamic mechanical properties of aluminum honeycomb and its effect factors［J］.Explosion and Shock Waves，2012，32（1）：23－28.

［9］Hu L L，You F F，Yu T X.Crushing strength of honeycombs with various cell wall angles［J］.Materials Research Innovations，2010，15（s1）：155－157.

［10］Liu Y，Zhang X C，The influence of cell micro－topology on the in－plane dynamic crushing of honeycombs［J］.International Journal of Impact Engineering，2009，36（1）：98－109.

［11］張新春，劉穎，章梓茂.組合蜂窩材料面內(nèi)沖擊性能的研究［J］.工程力學(xué)，2009，26（6）：220－225.Zhang Xin－chun，Liu Ying，Zhang Zi－mao.Research on dynamic properties of suppercell honeycomb structures under in－plane impact loading［J］.Engineering Mechanics，2009，26（6）：220－225.

［12］胡玲玲，余同希.慣性效應(yīng)對(duì)蜂窩能量吸收性能的影響［J］.兵工學(xué)報(bào)，2009，30（增刊2）：144－147.Hu Ling－ling，Yu Tong－xi.Influence of inertia effect on the energy absorption of hexagonal honeycombs［J］.Acta Armamentarii，2009，30（suppl 2）：144－147.