對(1± 1)n 兩種系數(shù)展開式上線性區(qū)域的解析初步
——基于quot;牛頓三角形quot;性質(zhì)的研究與探討㈠

王以將 劉忠 王紅霞

(1.江蘇省阜寧縣羊寨鎮(zhèn)農(nóng)業(yè)經(jīng)濟服務(wù)中心,江蘇鹽城 224415;2.桂林理工大學(xué),廣西桂林 541006)

對(1± 1)n兩種系數(shù)展開式上線性區(qū)域的解析初步
——基于quot;牛頓三角形quot;性質(zhì)的研究與探討㈠

王以將1劉忠2王紅霞2

(1.江蘇省阜寧縣羊寨鎮(zhèn)農(nóng)業(yè)經(jīng)濟服務(wù)中心,江蘇鹽城 224415;2.桂林理工大學(xué),廣西桂林 541006)

“楊輝-牛頓三角形”已經(jīng)將二項系數(shù)的展開式表示為數(shù)圖化的圖形形式,然發(fā)現(xiàn)其延展出的可糅合性、命名性、滑動性、連貫性、線性區(qū)域這五種特性,可使牛頓三角形內(nèi)任意兩點間,都可建立起連貫性的關(guān)系式;將 (1± 1)n兩形式的系數(shù)展開式及其示圖,糅合成一個新的三角形“△”后,仍清晰反映兩形式系數(shù)的不同角度與方向上的點、行、列之間的線性連貫關(guān)系,可發(fā)現(xiàn)更多性質(zhì),新產(chǎn)生性質(zhì)公式275個。

性質(zhì)(含公式) 應(yīng)用公式 線性關(guān)系區(qū)域 不同角度與方向

二項式系數(shù)的展開已經(jīng)組成“楊輝-牛頓三角形”,在此基礎(chǔ)上,我們依據(jù) (a+ b )n與 (a-b )n形式或合略稱 (1± 1)n兩形式所組成的三角形的可揉合性,結(jié)合成一個新的三角形“△”后,其各自部分仍保持原有的性質(zhì)不變．通過數(shù)圖化的圖形形式,發(fā)現(xiàn)其延展出的可揉合性、命名性、滑動性、連貫性、線性區(qū)域這五種特性,其中最重要兩點命名性、連貫性,可使牛頓三角形內(nèi)任意兩點都可建立起連貫的線性關(guān)系式．且由一點起經(jīng)與有關(guān)行或列上的移動性連續(xù)運算是本文的主要方法與特點,可省卻大量繁重的歸納演繹推導(dǎo)；故新三角形“△”,仍清晰反映不同角度與方向上的點、行、列之間的線性連貫關(guān)系,新產(chǎn)生性質(zhì)公式275個。

1 新三角形“△”具有的五種特性

牛頓三角形對于 (1+ 1)n形式系數(shù)展開式采用了數(shù)字表示法,據(jù)此也可將 (1- 1)n形式三角形表示出來．并根據(jù) (1± 1)n兩形式三角形的五種特性所構(gòu)成不同角度與方向上的線性區(qū)域及線性連貫關(guān)系。以示圖形式作一簡要描述,見圖1-1。

(1)可揉合性。新三角形“△”,仍可以保持它們各自原有的一些性質(zhì)定理的存在,同時以行n’為界線行置于 (1- 1)n的可視起始處,自然分為上、下各自部分,在閱讀上仍較方便．

圖1-1

(2)可命名性。除了行的概念外,圖中有列的概念,即對每一斜向的列可進行命名．而斜列的表示法,如圖:由上右至下左方向排列的分別稱第1、2、3、…左斜列,用符號“1/”、“2/”、“3 /”、……表示；由上左至下右方向排列的分別稱第1、2、3、…右斜列,用符號“1”、“2”、“3”、……表示。例某一點或(-),可表示在第n行上,同時在第“(m+1)/”上,也在第“(n-m+1)”上．從圖形上反映標示位置,左斜列在圖形右側(cè),右斜列在圖形左側(cè)。

(3)可滑動性。以界線行n’為滑動線,作上、下、左、右滑動,都可反映兩形式的上、下各自部分的正、負符號的隨機變化。如實現(xiàn)在計算機應(yīng)用領(lǐng)域能自動控制滑動則更好。當處于 (1+ 1)n形式時,每項(點)前符號都屬于正號；處于 (1- 1)n形式時,每上標為零與偶數(shù)位項時屬于正號,每上標為奇數(shù)位項時屬于負號。

(4)可連貫性。新三角形“△”內(nèi)部,任一最小的倒等邊三角形“ ▽”的三個相鄰項(點)之間都存在6個互逆的關(guān)系式,由此外延,對應(yīng)于某一原項(點)P0[稱Cmn或(±)]的其它項(點)Pr,都存在對應(yīng)于原點 P0的線性連貫關(guān)系式,且通過示圖及移動運算式可得到推導(dǎo)[將“△”左或右外的項(點)的值為0時,在圖形中用空項“□”符號表示其位置]。

(5)線性區(qū)域。若干對應(yīng)于某一項(點)P0的其它項(點)Pr,都存在對應(yīng)于原點P0的角度問題,可用公式0．5H)]來表達[I、H分別表示橫、縱向上的移動運算步(項)數(shù)]。但公式使用起來多數(shù)情況下其角度難以確切表示．但某些角度仍可確切掌握清晰,例每相隔30度的0°、30°、60°、90°、120°、150°、180°、210° 、240°、270°、300°、330°這12個方向的對應(yīng)角度項(點)。

根據(jù)科學(xué)出版社出版的,由胡國定等編寫的《簡明數(shù)學(xué)詞典》2000年11月第1版第9章“組合數(shù)學(xué)-圖論”中第495頁的兩處介紹組合數(shù)性質(zhì)與組合恒等式[及同包含龍門書局出版社2002年1月第1版源流等編寫的《發(fā)散課堂大思維》·高二代數(shù)(下)·試驗本第158頁],目前排列數(shù)、組合(數(shù))恒等式有9個]共有10個。而據(jù)http://baike．so．com/doc/5534332．html網(wǎng)國外狀況部分介紹“:組合數(shù)學(xué)在國外早已成為十分重要的學(xué)科,甚至可以說是計算機科學(xué)的基礎(chǔ)。一些大公司,如IBM,ATamp;T都有全世界最強的組合研究中心。Microsoft 的Bill Gates近來也在提倡和支持計算機科學(xué)的基礎(chǔ)研究。例如,Bell實驗室的有關(guān)線性規(guī)劃算法的實現(xiàn),以及有關(guān)計算機網(wǎng)絡(luò)的算法,由于有明顯的商業(yè)價值,顯然是沒有對外公開的”。根據(jù)胡國定等編寫的《簡明數(shù)學(xué)詞典》提及的10個組合數(shù)性質(zhì)與恒等式進行比照,例(見參考文獻[1])( ±)=(±)+(?):

(1)組合數(shù)性質(zhì)[帕斯卡公式(Pascal)]；

(2)組合恒等式(combinatirial identity)。

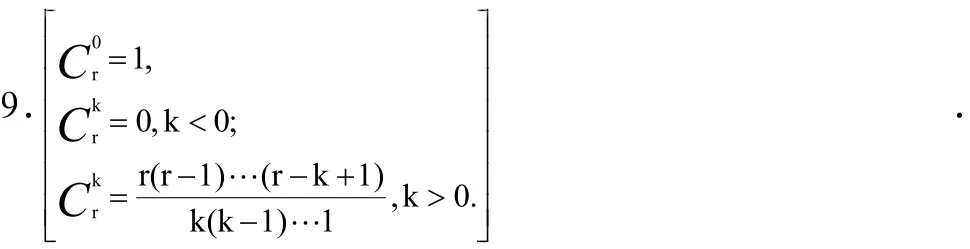
其中除5．6．8．9．中的部分外,大部分能在本文的移動運算中找到它們的存在之處。

鑒于此本文從任一行與緊鄰下一行上或任一列與緊鄰一側(cè)列上的兩點間的可產(chǎn)生的運算關(guān)系式類型,進行多種方向上的關(guān)系式類型的推導(dǎo)。產(chǎn)生新性質(zhì)(含公式)94個,另含附類屬公式181個合275個,預(yù)計產(chǎn)生應(yīng)用公式3760個,總推得公式3854個,另有14處為原已存在的性質(zhì)公式即原有恒等式(以下“結(jié)果值”一詞簡化用符號“※”表示)。

2 新三角形“△”內(nèi)一行上的一般線性連貫關(guān)系

指完全一行上的前、后半數(shù)項之和與中項問題,及隔位項之和問題分兩部分說明,存在性質(zhì)(含公式)1～12合12個,其中新產(chǎn)生性質(zhì)公式8個。

2.1 完全一行上的前、后半數(shù)項之和與中項問題

存在新產(chǎn)生性質(zhì)(含公式)1～8合8個。

2.1.1 對于 (1+ 1)n形式

完全一行上的前、后半數(shù)項之和相等且都為2n-1,⑴．當n為偶數(shù)時,前、后半數(shù)項之和同加單一最中間項的一半,其值為2n-1；⑵．當n為奇數(shù)時,前、后半數(shù)項之和分別加前、后相等的兩個最中間項,其值相等都為2n-1．存在新性質(zhì)(含公式)1～2合2個。

⑴．當n為偶數(shù)時(共含奇數(shù)個項),前、后半數(shù)項之和同加單一最中間項的一半 1 /2時,其值為2n-1,見圖2-4．性質(zhì),公式1；

圖2-4

⑵．當n為奇數(shù)時(共含偶數(shù)個項),前、后半數(shù)項之和分別加兩個前、后相等的最中間項時,其值相等都為2n-1,見圖2-5．性質(zhì)

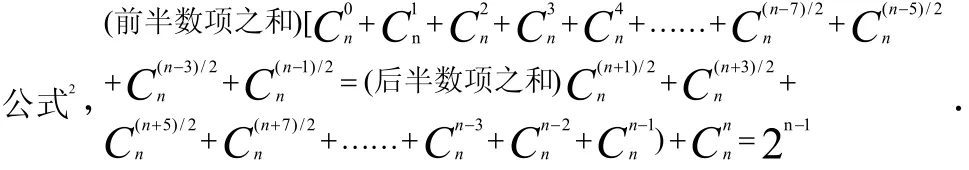
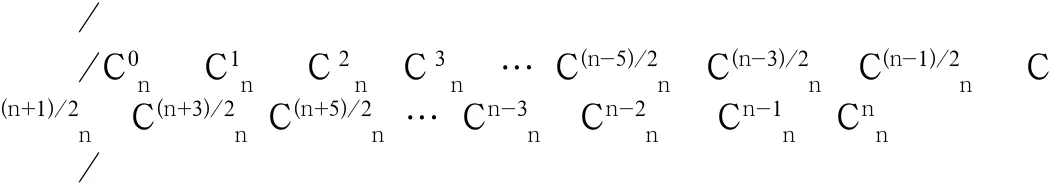
圖2-5

2.1.2 對于 (1- 1)n形式

存在⑴．當n為偶數(shù)時,完全一行上的前、后半數(shù)項之和(同加本行單一最中間項)相等,其值為上一(奇數(shù))行的同左斜列項即后一中間項[且n/2為偶數(shù),即n≡mod(4,0)]或( -)[且n/2為奇數(shù),即n≡mod(4,2)],且當n為偶數(shù)時,前、后半數(shù)項之和僅同加本行單一最中間項的一半,其和值為0；⑵．當n為奇數(shù)時(有前、后兩個最中間項),前、后半數(shù)項之和互為相反數(shù),其值為上一(偶數(shù))行的同左斜列項即單一最中間項[且n為奇數(shù),即(n-1)/2為偶數(shù)≡mod(4,2)]或[且n為奇數(shù),即(n-1)/2為偶數(shù)≡mod(4, 0)]．存在新性質(zhì)(含公式)3～8合6個。

下面分別敘述:(1)．當n為偶數(shù)時(共含奇數(shù)個項,僅含1個最中間項),(1)-①．且n/2為偶數(shù),即n≡mod(4,0),見圖2-6．因自上一行一端起與本行的連續(xù)運算(同加本行單一最中間項)的結(jié)果值等于上一行的同左或同右斜列項上的值,證明過程如下(以下此推導(dǎo)證明方式相同；故從略):

因其同一行上前、后半數(shù)項之和是相等的,所以(此處同加本行單一最中間項),其值為上一(奇數(shù))行的同左斜列項即后一中間項

圖2-6

⑴-②．且n/2為奇數(shù),即n≡mod(4,2),見圖2-6．前、后半數(shù)項之和相等[此處同加本行單一最中間項(-)],其值為上一(奇數(shù))行的同左斜列項即后一中間項 (-),性質(zhì)

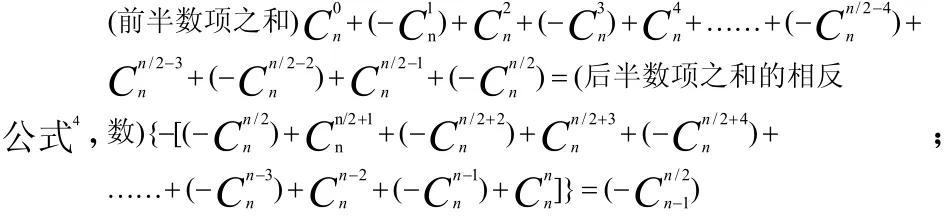
⑴-③．并n/2為偶數(shù),即n≡mod(4,0),前、后半數(shù)項之和相等且僅同加本行單一最中間項的一半 1 /2,其和值為0,因同時符合了上一(奇數(shù))行互為相反的前、后雙中間項之和為0,性質(zhì)

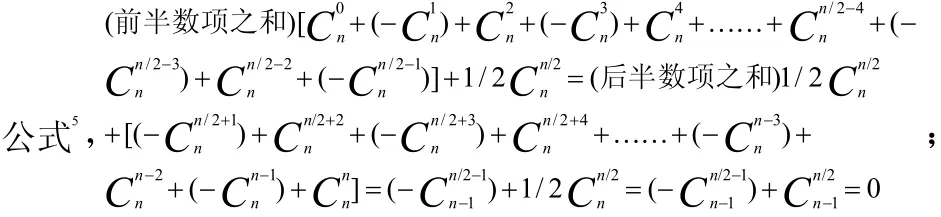
⑴-④．并n/2為奇數(shù),即n≡mod(4,2),前、后半數(shù)項之和相等且僅同加單一最中間項的一半 1/2( -),其和值為0,因同時符合了上一(奇數(shù))行互為相反的前、后雙中間項與( -)之和為0,性質(zhì)

(2)當n為奇數(shù)時(共含偶數(shù)個項,有前、后兩個最中間項),(2)-①．且(n-1)/2為偶數(shù)≡mod(4,2),前、后半數(shù)項之和互為相反數(shù),其值為上一(偶數(shù))行的同左斜列項即單一最中間項；(2)-②．且(n-1)/2為偶數(shù)≡mod(4,0),前、后半數(shù)項之和互為相反數(shù),其值為上一(偶數(shù))行的同左斜列項即單一最中間項見圖2-7。

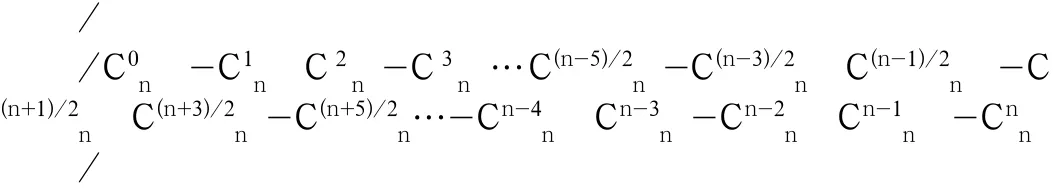
圖2-7

⑵-①．并(n-1)/2為偶數(shù)≡mod(4,2),前、后半數(shù)項之和互為相反數(shù){此處前、后分別加本行兩個最中間項其值為上一(偶數(shù))行的同左斜列項即單一最中間項C(n-1)/2,見圖2-7．性質(zhì)。

IKAnalyzer 是一個開源的基于Java 語言開發(fā)的輕量級的中文分詞工具包，結(jié)合詞典分詞和文法分析算法，正向最大匹配，原則是有效文本長度越長、詞元個數(shù)越少、路徑跨度越大、歧義詞詞元隊列位置越靠后、詞元位置權(quán)重越大等。

（2)-②．并(n-1)/2為偶數(shù)≡mod(4,0),前、后半數(shù)項之和互為相反數(shù){此處前、后分別加本行兩個最中間項其值為上一(偶數(shù))行的同左斜列項即單一最中間項 [- C(n-1)/2],見圖2-7．性質(zhì)。

2.2 完全一行上的隔位項之和問題

存在性質(zhì)(含公式)9～12合4個,全為原已存在的性質(zhì)公式。

2.2.1 對于 (1+ 1)n形式

完全一行上的偶、奇數(shù)位隔位項之和相等同為2n-1,存在性質(zhì)(含公式)9～10合2個．得出2個性質(zhì)(含公式)同屬于原有恒等式。

⑴．當n為偶數(shù)時(共含奇數(shù)個項),偶、奇數(shù)位隔位項之和的值都為2n-1,參考見圖2-4．性質(zhì)公式9(此符合原已存在性質(zhì)公式)(上標偶次項和)(上標奇次項和)即屬原有恒等式n正整數(shù)。

⑵．當n為奇數(shù)時(共含偶數(shù)個項),偶、奇數(shù)位隔位項之和的值都為2n-1,參考見圖2-5．性質(zhì)公式10(此符合原已存在性質(zhì)公式),(上標偶次項和即屬原有恒等式n正整數(shù)．

(1）．當n為偶數(shù)時(共含奇數(shù)個項),參考見圖2-6．偶、奇數(shù)位隔位項之和互為相反數(shù),其值分別為2n-1、(-2n-1),性質(zhì)公式11(此符合原已存在性質(zhì)公式),

2.2.2 對于形式 (1- 1)n無論n為偶或奇數(shù)

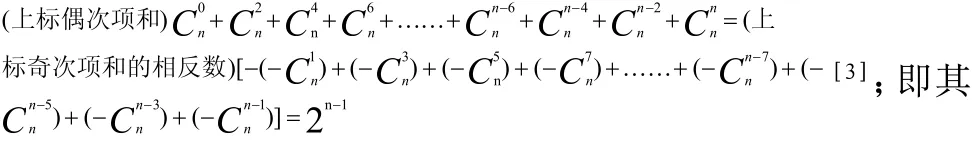
絕對值同屬于原有恒等式

K=0K=0

⑵．當n為奇數(shù)時(共含偶數(shù)個項),參考見圖2-7．偶、奇數(shù)位隔位項之和互為相反數(shù),其值分別為2n-1、(-2n-1),性質(zhì)公式12(此符合原已存在性質(zhì)公式),

[1]胡國定等.簡明數(shù)學(xué)詞典,北京:科學(xué)出版社,2000,11:495.

[2]源流等.發(fā)散思維大課堂,高二代數(shù)(下)·試驗本,北京:龍門書局出版社,2002,1:158.

王以將(1950—),男,農(nóng)藝師,漢族,江蘇阜寧人,畢業(yè)于江蘇農(nóng)學(xué)院.先后入編世界與國內(nèi)優(yōu)秀專家人才名典等.發(fā)表文章30余篇,獲國際與國內(nèi)優(yōu)秀獎57項;涉及數(shù)列應(yīng)用(農(nóng)業(yè)類)的“植物分枝(蘗)的兩種數(shù)學(xué)模型求解公式”一文在《中國科技財富》2009年第11期(下)登載.本文的前身是簡要的《用滑動性六翼形區(qū)域解牛頓三角形之謎》,在2003年“第二屆中國科學(xué)家”論壇上獲二等獎.現(xiàn)經(jīng)系統(tǒng)整理于下(全文約1200頁).