某發動機藥柱極端溫度發射結構完整性分析*

楊軍輝，雷勇軍，蒙上陽

(1國防科學技術大學航天科學與工程學院，長沙 410073;2 63961部隊，北京 100000)

0 引言

陸軍野戰火箭為了滿足火力迅速、猛烈、能全天候作戰使用的要求，一般采用大長徑比固體火箭發動機傾斜機動發射，發動機在使用過程中要經歷各種載荷的考驗，特別是在點火發射階段，推進劑藥柱要承受內壓、過載、熱載荷等聯合作用，增壓速率高、軸向過載大(一般在20 g以上)，是火箭發動機最容易發生結構完整性問題的時刻。此外，為了滿足不同地域、不同環境下的使用要求，陸軍野戰火箭發動機必須考慮極端環境溫度下發射時的結構完整性問題。目前，國內對固體火箭發動機在單獨載荷作用下的結構完整性研究較多［1-6］，但對分段式大長徑比固體火箭發動機在極端溫度、高過載和點火增壓聯合作用下的結構響應及其結構完整性研究并不多見。因此，有必要對這一類型固體火箭發動機在極端溫度條件下發射時的結構完整性進行研究，這對于作戰使用和工程設計具有重要意義。

文中以某野戰火箭固體發動機為例，采用三維熱粘彈性有限元方法，在內壓、軸向過載和溫度載荷(－40℃、+50℃)聯合作用下進行了數值仿真，得到了發動機藥柱的位移、應力和應變場，并對其結構完整性進行評估，研究結果可為分段式大長徑比固體火箭發動機設計和使用提供參考。

1 計算模型

1.1 本構關系和有限元方程

復合固體推進劑屬于粘彈性材料，其本構關系有微分型和積分型兩種形式，積分型本構關系由于更有利于數值計算的實現而得到了廣泛的應用。假設推進劑為各向同性的熱流變簡單材料，不考慮物理非線性，積分型粘彈性本構關系可寫成［7］:

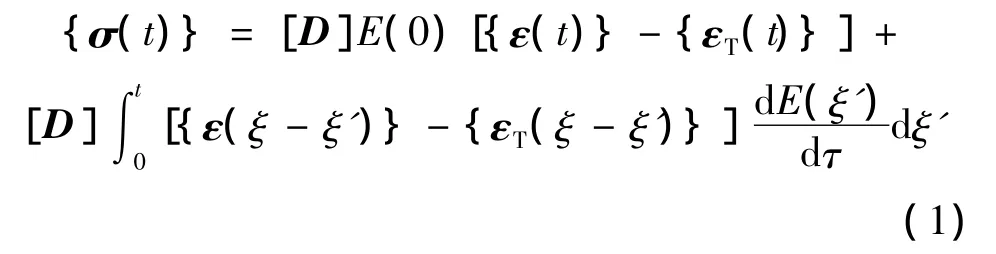
式中:{σ}、{ε}和{εT}分別為應力張量、應變張量和溫度應變張量;E(0)為初始模量，E(t)為松弛模量，［D］為粘彈性矩陣。將松弛模量E(t)表示成Prony級數的形式，并將式(1)在時域中離散，得到增量型本構方程:

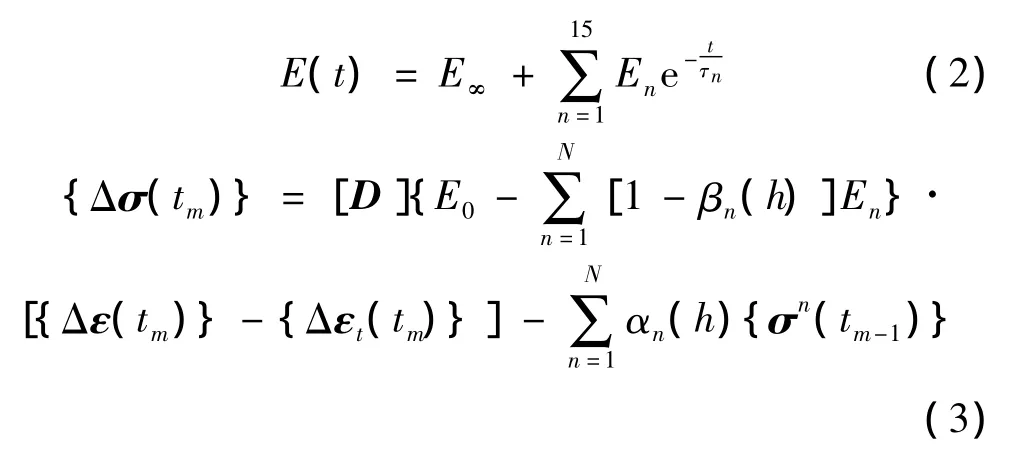
式(2)中 E∞為持久模量，En、τn為第 n個 Maxwell單元的彈性模量和松弛時間;式(3)中Δσ(tm)、Δε(tm)和Δεt(tm)分別為應力張量、應變張量和溫度應變張量在tm時刻的增量，αn(h)、βn(h)是只和推進劑松弛模量和計算時間步長h相關的參數。

將式(3)代入增量形式的虛功方程中，最終得到增量型有限元方程:

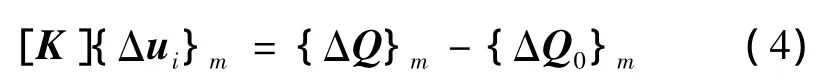
式中:［K］、{Δui}m、{ΔQ}m、{ΔQ0}m分別為 t時刻非線性剛度矩陣、節點位移增量、節點外載荷增量和初始外載荷增量，具體表達式見文獻［7］。

1.2 發動機藥柱有限元模型

以某大長徑比固體火箭發動機為例，該發動機為2段式結構，前段藥柱為5星型，后段藥柱為管形，整個發動機由殼體、絕熱層、推進劑、應力釋放罩構成，長徑比為12.3。利用載荷的軸對稱性和發動機藥柱幾何結構的循環對稱性，取其中1/10建立三維有限元計算模型，共劃分71 146個六面體單元，節點總數為84 265個，如圖1所示。

圖1 發動機藥柱三維有限元模型

根據對稱性，對稱剖面上位移邊界條件uθ=0，發動機殼體前段位移邊界條件ur=uθ=uz=0。

1.3 材料力學性能參數

發動機殼體彈性模量205 GPa，泊松比0.3，密度7.8 g/cm3，熱膨脹系數 1.2E-5。絕熱層、包覆層和推進劑的泊松比高溫時取0.497，低溫時取0.495;密度按測量值取;絕熱層、包覆層和推進劑熱膨脹系數分別為8.5E-5、8.5E-5 和8.8E-5。

絕熱層、包覆層和推進劑松弛模量用Prony級數表示，推進劑20℃時持久模量E∞=0.576 MPa，Prony級數取其中6項，見表1。絕熱層和包覆層松弛模量分別按推進劑松弛模量的0.9和2.0倍計算。藥柱時-溫等效因子(WLF方程)如下:

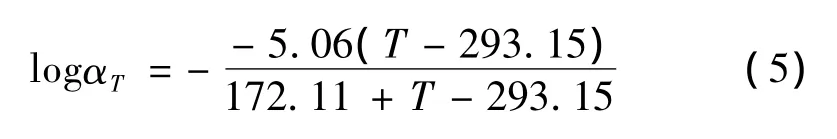
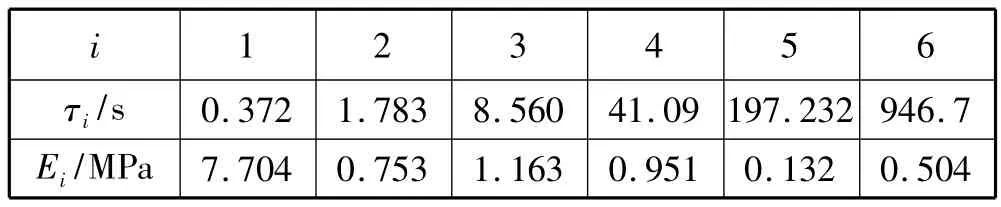
表1 Prony級數參數

2 載荷工況

在高溫和低溫兩種工況下對藥柱結構響應進行分析:高溫環境下點火發射時，發動機由零應力溫度降到+50℃后，再加載內壓和軸向過載;低溫環境下點火發射時，發動機由零應力溫度歷時一天下降至低溫－40℃，再加載內壓和軸向過載。發動機藥柱在固化過程中，其零應力溫度為+58℃，當環境溫度變化時，假設其規律線性變化，在任一時刻整個發動機溫度場是均勻的。發動機點火后建壓時間為200 ms，最大內壓值13 MPa，由于建壓時間短，不考慮燒蝕效應。發射時軸向過載為20 g，并假設在整個過程中加速度不隨時間改變。

3 位移、應力和應變分析

3.1 位移場計算結果

發動機藥柱在高溫+50℃和低溫－40℃發射時的位移幅值計算結果如圖2、圖3所示，位移幅值沿翼槽特征線(藥柱前段沿翼槽軸向，后段沿內表面軸向)的分布規律如圖4所示。

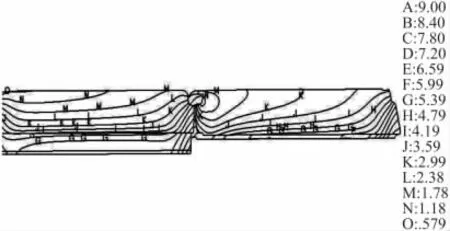
圖2 高溫發射時藥柱位移幅值場等值線

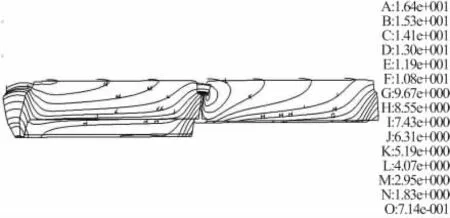
圖3 低溫發射時藥柱位移幅值場等值線

從計算結果可見，高、低溫點火發射時，在軸向內壓和過載的共同作用下，位移最大值均出現在后段藥柱的尾部，且低溫發射時位移幅值要大于高溫發射時位移幅值。高溫點火發射時位移最大值為9.3 mm，是后段藥柱長度的0.5%;低溫點火發射時位移最大值為16.4 mm，是藥柱長度的0.89%，形變相對量不大。

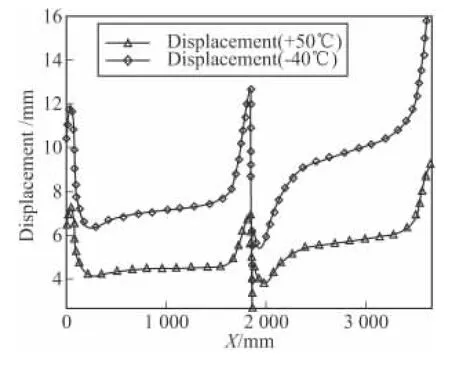
圖4 藥柱位移幅值沿翼槽特征線分布規律

3.2 應變場計算結果

無缺陷固體推進劑藥柱破壞準則一般采用八面體剪應變準則較為合理［8］，Von Mises應變準則與八面體剪應變準則本質上是等效的，因此文中用Von Mises應變準則作為藥柱結構完整性判據。圖5、圖6與圖7描述了高溫、低溫點火發射時推進劑藥柱Von Mises應變場分布及沿軸向特征線變化的規律。計算結果表明高溫、低溫點火發射載荷導致推進劑藥柱三向受壓，推進劑藥柱前段翼槽中部、后段圓管中部均存在Von Mises應變集中，其中，在發動機藥柱前段翼槽中部對應處的Von Mises應變為全局最大值。由圖5高溫發射時藥柱Von Mises應變場等值線、圖7藥柱Von Mises應變沿翼槽特征線分布規律可見，高溫發射時Von Mises應變最大值為14.6%，后段中部的Von Mises應變為10.6%，推進劑的高溫許用應變為40%，安全系數為2.74，高溫點火發射時推進劑藥柱的結構完整性滿足要求。

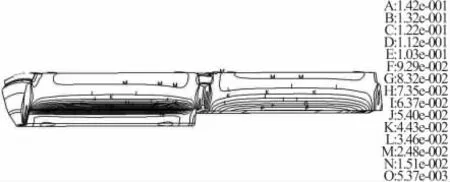
圖5 高溫發射時藥柱Von Mises應變場等值線

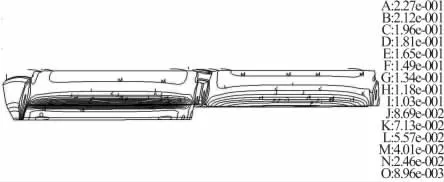
圖6 低溫發射時藥柱Von Mises應變場等值線

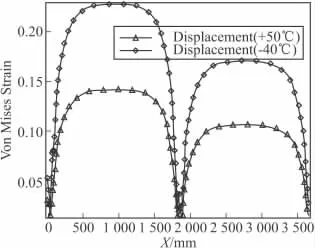
圖7 Von Mises應變沿翼槽特征線分布規律

低溫發射時推進劑藥柱的Von Mises應變水平是考驗發動機藥型優劣的重要參數之一，由圖6低溫發射時藥柱Von Mises應變場等值線、圖7藥柱Von Mises應變沿翼槽特征線分布規律可見，低溫發射時藥柱Von Mises應變最大值為23.5%，后段中部的Von Mises應變為10.6%，推進劑的低溫許用應變為58%，安全系數為2.46，低溫點火發射時推進劑藥柱的結構完整性滿足要求。從圖5、圖6和圖7可見在點火發射時推進劑藥柱承載分布較為均勻合理，沒有特別尖峰的突變應變值出現。

3.3 應力場計算結果

推進劑藥柱的Von Mises應力場的分布規律可以反映出藥柱承受應力水平的高低，也是評估發動機藥型優劣的一個參考指標，因此有必要探討推進劑藥柱的應力場。高溫、低溫點火發射時推進劑藥柱Von Mises應力場的分布規律與Von Mises應變場的分布規律是一致的，即在前翼槽處、圓柱段中部出現應力集中，Von Mises應力在藥柱前翼槽處達到最大值。由圖8 Von Mises應力沿翼槽特征線分布規律可見，高溫、低溫發射時發動機藥柱前翼槽中部的 Von Mises應力最大值分別為 1.69 MPa 和 1.3 MPa，后段中部的Von Mises應力最大值分別為1.22 MPa和0.91 MPa。

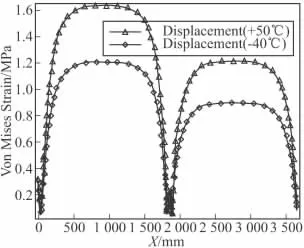
圖8 Von Mises應力沿翼槽特征線分布規律

4 結論

文中通過采用三維熱粘彈性有限元方法，得到了一種大長徑比陸軍野戰火箭固體發動機推進劑藥柱在高溫和低溫點火發射時的位移、應變和應力場分布規律，并對其結構完整性進行評估，主要結論如下:

1)發射時藥柱在內壓和軸向過載作用下是收縮的，前后兩段藥柱均是兩端位移較大，中間位移較小。位移最大值出現在藥柱圓柱段后端，高溫和低溫發射時分別為 9.3 mm、16.4 mm，是推進劑藥柱長度的0.5%和0.89%，形變相對量不大，各組成部分在工作中無相互擠壓，剛度滿足要求。

2)高溫和低溫點火發射時推進劑藥柱三向受壓，推進劑藥柱前段翼槽中部、后段圓管中部均存在Von Mises應變、應力集中，其中，藥柱前段翼槽中部對應處的Von Mises應變為全局最大值。高溫、低溫發射時藥柱 Von Mises應變最大值分別為 14.6%和23.5%，安全系數分別為2.74 和2.46，滿足無缺陷固體推進劑藥柱結構完整性要求。

3)高、低溫點火發射時推進劑藥柱沒有特別尖峰的突變應力、應變值出現，承載分布較為均勻合理。

［1］于洋，王寧飛，張平.溫度載荷下帶筋套管形裝藥結構完整性分析［J］.推進技術，2006，27(6):492-496.

［2］王玉峰，李高春，劉著卿，等.變溫環境下固體藥柱的溫度應力分析［J］.宇航學報，2010，31(9):2223-2230.

［3］孟紅磊，周長省，鞠玉濤，等.非均布瞬態內壓作用下星孔藥柱應力分析［J］.固體火箭技術，2010，33(3):289-293.

［4］劉中兵，利鳳祥，李越森，等.高過載條件下固體推進劑藥柱結構完整性分析計算［J］.固體火箭技術，2003，26(2):12-16.

［5］劉華，李旭昌，馮錦虎，等.固體推進劑藥柱在振動載荷作用下的結構完整性分析［J］.戰術導彈技術，2009(5):10-14.

［6］李恩奇，雷勇軍，袁端才，等.某固體火箭發動機藥柱的動力學分析［J］.固體火箭技術，2007，30(6):486-489.

［7］蒙上陽.基于粘彈性有限元方法的固體火箭發動機結構完整性分析［D］.長沙:國防科技大學，2005.

［8］陳汝訓.固體火箭發動機設計與研究［M］.北京:宇航出版社，2005.