鴨舵修正機構舵偏角選擇方法*
邵 盼,郭煜洋,郝永平,張 華
(沈陽理工大學兵器科學技術研究中心,沈陽 110159)
0 引言
目前精確打擊彈藥在信息化戰爭中有著非常重要的作用,其中二維彈道修正彈成本較低并具有一定的打擊精度,而修正能力是保證打擊精度的基礎。二維彈道修正的方式主要分為鴨舵修正和微小型推進器修正,其中微小型推進器修正對彈丸的修正能力次數是有限的,并且在引信中集成的難度系數很大,而鴨舵修正能對彈丸實施較為平穩的修正,修正能力連續靈活,且可以對較長飛行時間的彈丸彈道進行修正,是目前二維彈道修正技術的主要方法。
文中以某普通制式彈丸為研究對象,使用固定式鴨舵對其進行二維彈道修正。首先分析了不同舵偏角下彈丸的氣動特性,并運用ADAMS仿真得到不同舵偏角下的彈丸飛行穩定性特征,綜合考慮電機控制能力和修正能力得出合理選擇鴨舵舵偏角的方法。
1 固定式鴨舵修正彈修正方法
鴨舵式二維彈道修正彈的修正機構主要包括舵翼、探測系統、控制系統、引信激發裝置等,修正執行機構主要是兩對帶偏角的舵翼,其中一對是減旋舵,另一對是修正舵。當減旋舵受到空氣動力作用時,導致引信的導轉力矩與原旋轉方向相反,為控制引信提供部分動力。當需要修正偏移量時,修正舵會提供所需的氣動力。可見修正舵對彈丸的修正效果有很大的影響,而不同的舵偏角又對舵片的選擇具有重要的意義,所以合理的舵偏角是保證彈道修正彈打擊精度的必要條件之一。二維彈道修正原理如圖1所示:當需要打擊某一目標時,在彈丸發射前將目標落點的相關參數輸入到二維彈道的修正引信中,彈丸發射后,引信中的彈載系統結合彈丸的發射初始條件和目標參數,計算出理論彈道;在彈丸飛行過程中,彈丸的實時飛行參數傳給彈丸的探測裝置,彈載系統對此進行計算得到實際彈道,并與理論彈道的相關數據進行比較,對彈道進行俯仰和偏航修正。當偏差達到預先設置的修正量極限時,控制系統就會利用修正機構對彈道進行修正,從而可以更好的導向目標落點,實現提高打擊精度、高效毀傷目標的目的。
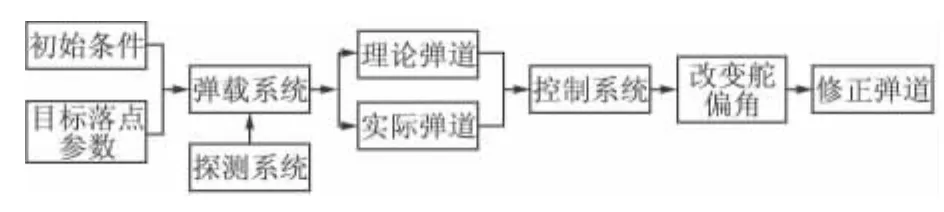
圖1 鴨舵式二維彈道修正彈修正系統原理圖
2 不同舵偏角氣動特性分析
二維修正彈的修正鴨舵迎風面積相同,舵偏角度數不同時對彈丸的氣動特性是有影響的,而且不同的偏角度數對彈丸的整體氣動特性的影響也是不同的,直接影響著舵翼的側向力、導轉力矩和整個彈丸的阻力、翻轉力矩等方面,可能會使彈丸在飛行過程中出現翻轉、過穩定等情況,影響彈丸的打擊能力,故選擇合理的舵偏角同樣是保證彈丸修正機構氣動布局設計合理的重要條件。
為了觀察鴨舵式二維彈道修正舵偏角對全彈氣動特性的影響,以確定合理的舵偏角。在此以某炮彈為研究背景設計了舵翼迎風面積、形狀、位置等相同,舵偏角不同的仿真模型,其中彈丸布局如圖2所示。

圖2 鴨舵機構與全彈布局簡圖
現建立以非對稱舵為例,分別取舵偏角2°、4°、6°、8°、10°、12°、14°的仿真模型進行氣動仿真,得到圖3~圖5的結果。
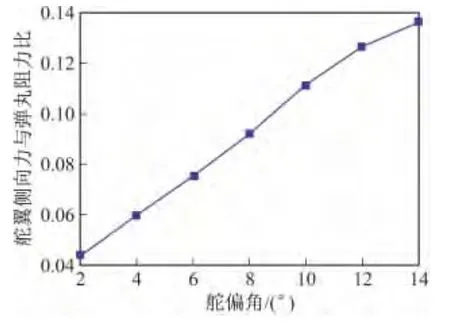
圖3 舵偏角大小對舵翼側向力與彈丸阻力之比影響
從圖3中可以看出,舵翼側向力與彈丸阻力的比例關系是隨著舵偏角的增加而有增大趨勢的,其中2°~8°偏角時,比例關系基本呈線性關系。
從圖4可以看出,彈丸翻轉力矩隨舵偏角的增大而增加,其中2°~12°偏角時,比例關系基本呈線性關系,舵偏角增加的幅度比較大,這對彈丸的穩定性影響比較大。
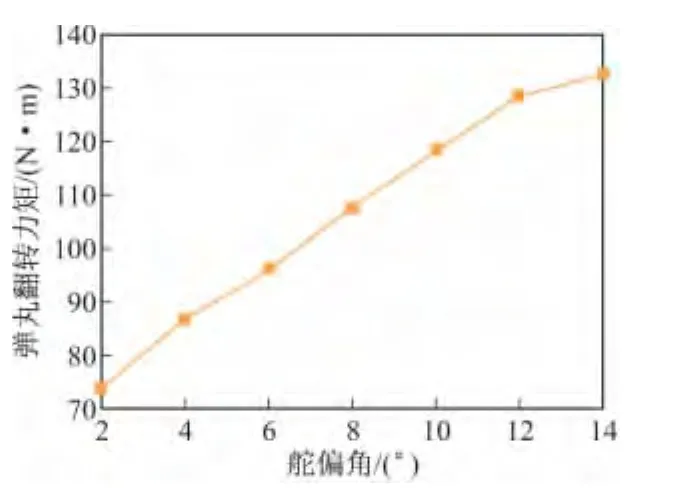
圖4 翻轉力矩與舵偏角關系
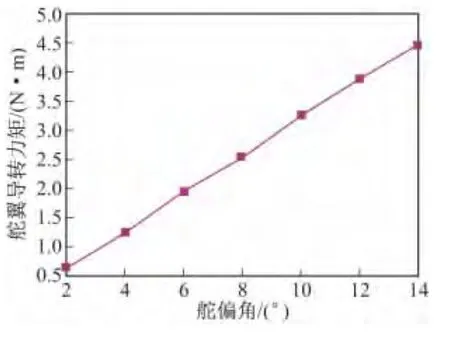
圖5 舵翼導轉力矩與舵偏角關系
從圖5中可以看出,舵翼導轉力矩隨著舵偏角的增加呈線性關系增加,由于引信部分的轉動慣量一定,當導轉力矩越大則引信旋轉的速度越快,對電機的要求越高。若選擇的舵偏角過大,則會因無法選擇合適的電機而不能實現彈丸的合理設計。
以2°、6°、10°舵偏角時的壓力等值線圖為例,如圖6比較可以看出:不同的舵偏角所展現出的彈丸周圍云圖有明顯差異。

圖6 數值模擬仿真
從以上分析可以看出,舵偏角對彈丸的舵翼升力、舵翼導轉力矩、彈丸翻轉力矩影響是非常明顯的,其中舵偏角越大彈丸舵翼的升力、導轉力矩以及彈丸的翻轉力矩越大。
3 邊力學仿真分析
以某普通制式彈丸為基礎的修正彈,在射角50°,初速800 m/s等初始條件下,基于動力學分析軟件,結合彈丸在飛行過程中,受靜不穩定力矩的作用,在擾動產生攻角及彈丸在重力作用下彈道出現彎曲等的影響。通過動力學仿真分析,得到不同舵偏角下修正彈丸的實時運動狀態。其中舵偏角在6°及以下時彈丸均能克服上述影響,從而滿足陀螺穩定性、動態穩定性、追隨穩定性,進行穩定的全彈道飛行,而在8°偏角時則修正彈丸無法完成穩定的全彈道飛行。其中部分偏角下的彈丸飛行狀態動態情形如圖7、圖8所示。

圖7 6°舵偏時彈丸穩定運動姿態

圖8 8°舵偏時彈丸不穩定運動狀態
通過動力學仿真可以觀察到,當舵偏角為6°時,修正彈丸的外彈道飛行是穩定的。舵偏角達到8°時,修正彈丸的飛行狀態是不穩定的,出炮口后彈丸很快出現翻轉。同理,可以知道當舵偏角大于8°時,修正彈丸的飛行是不穩定的。
4 電機控制能力分析
固定在彈丸頭部位置的鴨舵,包含一對減旋舵和一對修正舵,其中減旋舵受空氣作用而產生的導轉力矩與電磁力矩結合起來共同控制引信的低速旋轉及目標姿態。減旋舵的導轉力矩的變化趨勢如圖9所示。
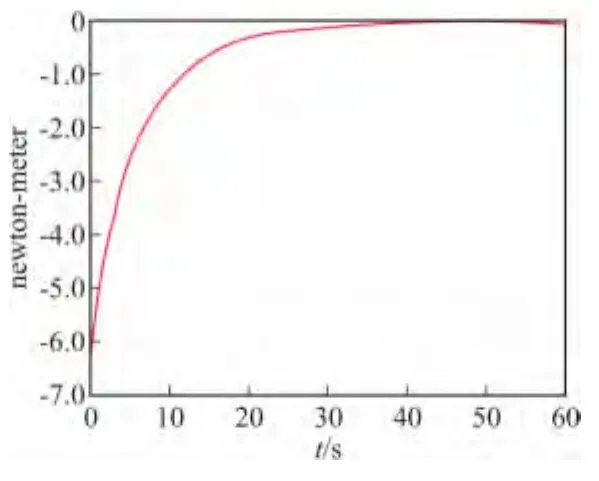
圖9 6°舵偏角時減旋舵導轉力矩變化
從圖9中引信的導轉力矩變化趨勢可以看出,在彈丸出炮口后10 s的時間內,導轉力矩變化率很大,且力矩的值變化也很大。在10 s以后,導轉力矩變化率較小,且力矩值的變化也相對較小。
結合上述的導轉力矩變化趨勢,利用電機對引信姿態進行控制,當電機的電磁力矩取值范圍在1.5 N·m內時,設定在出炮口5 s后開始控制引信滾轉在目標姿態,則在5~80 s的控制范圍之內,引信實際被控制的時間是13~80 s,如圖10所示。
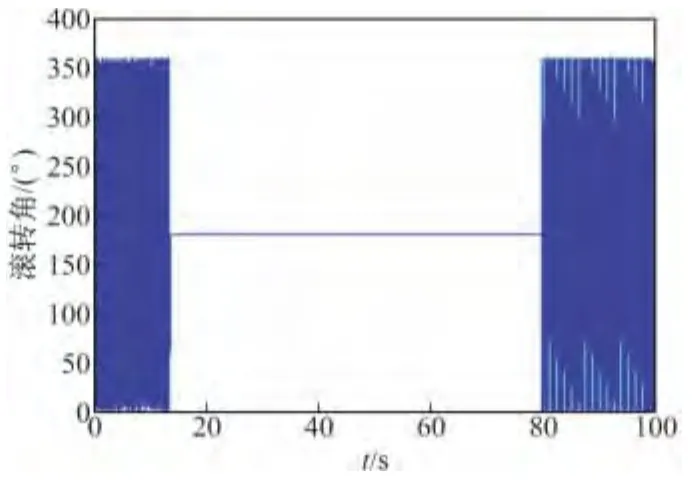
圖10 電磁力矩在1.5 N·m內時的控制能力
當電機的電磁力矩取值范圍在2.0 N·m范圍內時,同樣設定在炮彈出炮口后5 s時起控,則在5~80 s的控制范圍內,引信實際被有效控制的時間是7~80 s,如圖11所示。

圖11 電磁力矩在2 N·m內時的控制能力
綜合以上可以得到,電磁力矩的取值直接影響引信姿態的控制時間,電磁力矩越大則對引信的控制能力越強,但對電機的要求會大大提高并會增加成本。
5 修正能力分析
以舵偏角為6°時的修正彈模型為例,已知該炮彈按照射角50°,初速800 m/s發射。在上述條件下的修正彈經過彈道方程解算,得到射程約為22.5 km。當修正舵處于特定位置時,它能為橫向修正提供側向力,而在特定時間內持續性的固定在某一值則能得到此位置下的最大修正能力,在此選取時間t=35 s處作為固定修正舵時間點并進行持續修正,來觀察舵偏角分別為2°、4°、6°時彈道修正效果如圖12。通過外彈道仿真分析,得到6°舵偏角時的修正量,如表1所示。
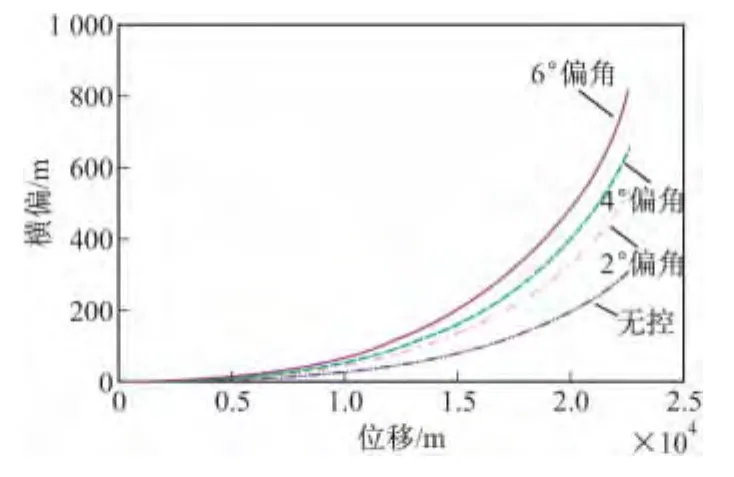
圖12 修正彈最大修正能力
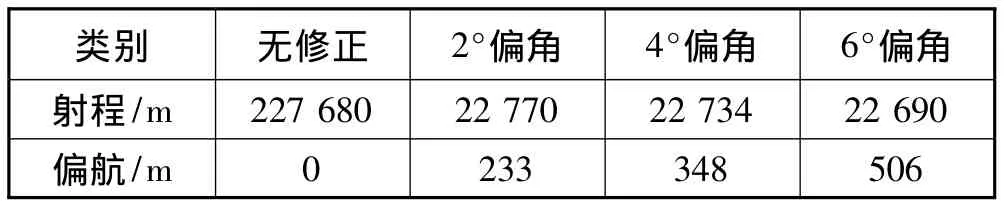
表1 彈丸修正能力與舵偏角關系
由結果可以看出,彈丸的修正能力與舵偏角有直接關系,舵偏角越大,彈丸的修正能力越強,但必須滿足彈丸的飛行穩定性和電機控制能力。
6 結論
文中重點探討了如何對固定式鴨舵修正機構舵偏角進行選擇,建立了不同舵偏時的氣動仿真模型,并得到了各情形下的氣動力數據,通過分析可以得出:舵偏角對彈丸翻轉力矩及舵翼升力影響較大,且舵翼升力隨著舵偏角的增大而增大;對鴨舵導轉力矩影響較大,且舵偏角越大則舵面導轉力矩越大。
建立了運動學仿真模型,通過對彈丸外彈道飛行狀態的模擬,可以看出當舵偏角在6°以下時,彈丸可以全彈道穩定飛行,但當舵偏角達到8°時,彈丸無法穩定飛行。
通過對電機控制能力的分析,可以得出舵翼導轉力矩的大小直接影響對電機的合理選擇。同時,電機的電磁力矩取值范圍也限制了舵偏角的取值。
通過利用適合修正彈的彈道模型對彈丸的修正能力進行仿真,得出了穩定飛行時不同舵偏角下的修正能力。
綜合以上得出,若要合理選擇舵偏角,須把彈丸的飛行穩定性、修正能力、電機的合理性等綜合考慮才能最終合理的選擇一種符合修正機構氣動布局的舵偏角。
[1]郝永平,孟慶宇,張嘉易.固定翼二維彈道修正彈氣動特性分析[J].彈箭與制導學報,2012,32(3):171-177.
[2]劉恒,霍鵬飛.彈道修正引信菱形翼型等腰梯形十字減旋翼[J].探測與控制學報,2009,31(6):47-50.
[3]韓子鵬.彈箭外彈道學[M].北京:北京理工大學出版社,2008:141-143.
[4]徐明友.火箭外彈道學[M].哈爾濱:哈爾濱工業大學出版社,2004:10-15.
[5]張嘉易,王廣,郝永平.二維彈道修正彈鴨舵修正機構氣動特性研究[J].彈箭與制導學報,2013,33(2):88-91.
[5]雷文星,田曉麗,吳建萍,等.一維彈道修正彈的氣動特性與修正量研究[J].彈箭與制導學報,2012,32(6):131-135.
[6]William J Larkin,Mitch Thomas.Atmospheric flight of a variable-bend body[J].Jounal of Guidance and Control,1979,2(5):382-387.
[7]Lock R C.Test cases for numerical methods in two-dimensional transonic flows,AGARD-R-575-70(AD715554)[R].1970.

