基于兩種瓶頸度的制造車間多瓶頸動態(tài)預測方法

劉 志 蔣增強 龔本剛

1.安徽工程大學，蕪湖，241000 2.北京交通大學，北京，100044

0 引言

現(xiàn)代制造模式下，制造企業(yè)的生產過程充滿了大量的不確定性因素，這使得其優(yōu)化控制日益困難。為降低制造車間優(yōu)化工作的難度，有學者將約束理論中的瓶頸概念加以拓展，提出了一種基于瓶頸的制造車間生產過程優(yōu)化方法［1－2］。該方法強調在復雜的制造環(huán)境中能快速識別影響系統(tǒng)整體性能的薄弱環(huán)節(jié)（系統(tǒng)瓶頸），并以此為中心，對生產過程加以分解，以降低制造車間生產過程優(yōu)化的難度，提高優(yōu)化的性能。瓶頸識別作為生產過程優(yōu)化的首要任務，其準確與否直接決定了優(yōu)化工作的時效性。目前，主要的瓶頸識別方法可歸結為3類：基于瓶頸外部表現(xiàn)特征（如將設備阻塞和饑餓時間［3－5］、設備持續(xù)活性時間［6－7］、設備負荷［8］、設備利用率［9］等作為系統(tǒng)瓶頸的特征）的識別方法、基于調度視覺的瓶頸識別方法［10－13］和基于能力負荷比的瓶頸識別方法［14－18］。

以上3種方法以預測系統(tǒng)的平均瓶頸為主，缺乏對瓶頸漂移過程的實時分析；同時，現(xiàn)有的3類瓶頸預測方法因各有特定的適用范圍，并不總是具有良好的可擴展性。方法1利用的瓶頸外部表現(xiàn)特征是瓶頸判定的必要條件，而不是充分條件，當系統(tǒng)處于飽和生產狀態(tài)時，很多設備的利用率均會達到比較高的相似水平，此時，運用設備利用率難以識別系統(tǒng)瓶頸。方法2定義了每個機器調度方案的變化對系統(tǒng)調度性能的影響，具有局部性和全局性，但只從調度角度考慮了瓶頸對系統(tǒng)性能的影響，不夠全面；同時，該方法需進行大量的仿真和實驗。方法3克服了前兩種方法存在的不足，但當系統(tǒng)存在多個瓶頸時，工序間的復雜相關性使得制造單元瓶頸責任并不總能得到有效的認定，使得具有最大能力負荷比的瓶頸單元（主瓶頸）的判定準則并不總是成立，導致無法準確預測系統(tǒng)真正的主次瓶頸。因此，本文在充分考慮制造單元相關性對瓶頸能力影響的基礎上，提出一種基于兩種瓶頸度的多瓶頸動態(tài)預測方法，以實現(xiàn)制造系統(tǒng)瓶頸的準確、連續(xù)預測。

1 兩種瓶頸度的描述

1.1 兩種瓶頸度的提出

在生產過程中，因各種不確定性因素的影響，任何一個制造單元都有成為瓶頸的能力，這一能力稱為瓶頸度［16］。瓶頸度是制造單元固有的一種動態(tài)屬性，是制造環(huán)境中各種不確定性因素的綜合作用結果。瓶頸度越大，制造單元成為系統(tǒng)瓶頸的概率越大，反之則越小。

在實際生產過程中，制造單元之間存在一定的相關性，導致制造單元成為瓶頸的能力可能部分依賴于前趨單元的制造能力和制造速度。將完全或部分依賴其他單元產出的瓶頸稱為非獨立瓶頸，將完全不依賴其他單元發(fā)生的瓶頸稱為獨立瓶頸。非獨立瓶頸可能會隨著獨立瓶頸的消除或被弱化（如次瓶頸隨著主瓶頸的消除而轉化為非瓶頸），或被強化。通常意義上的瓶頸度實質上是當前制造單元固有瓶頸能力、前趨單元制造能力和制造需求綜合作用的結果，在多瓶頸環(huán)境下，無法反映出系統(tǒng)各個瓶頸的獨立性，進而使得系統(tǒng)主次瓶頸的預測因缺乏制造單元相關性的合理分析而并不總是十分準確。因此，在文獻［16］的基礎上，提出兩種瓶頸度概念，以在認定制造單元瓶頸責任的基礎上，實現(xiàn)系統(tǒng)主次瓶頸的準確預測。

綜合瓶頸度（一般瓶頸度）指制造單元在外部要素（產品需求、原材料供應等）和固有要素（加工設備、操作人員等）共同影響下成為瓶頸的能力；獨立瓶頸度指制造單元在不考慮前趨單元影響（簡稱前影）、只在其固有要素影響下成為瓶頸的能力。

每個制造單元都有成為瓶頸的可能，因此，任何一個制造單元都存在兩種瓶頸度，且綜合瓶頸度不小于獨立瓶頸度。只有在下列情況下，兩種瓶頸度才相等：①生產系統(tǒng)的第一個制造單元上，若原材料、零部件的供應穩(wěn)定，為簡化分析，不考慮生產系統(tǒng)輸入的影響；②上下制造單元在技術上無任何聯(lián)系，此時，前趨單元的影響為0。

1.2 瓶頸指數(shù)和獨立瓶頸指數(shù)的數(shù)學描述

兩種瓶頸度是對制造單元運行狀態(tài)的一種綜合描述，而定性分析無法為生產過程的有效控制提供依據(jù)。目前，綜合瓶頸度通過瓶頸指數(shù)加以度量［16－17］，而獨立瓶頸度的度量方法則無相關研究，因此，以瓶頸指數(shù)IBN數(shù)學模型為基礎，綜合考慮制造單元之間的相關性，建立獨立瓶頸指數(shù)IBNI，來定量描述制造單元獨立瓶頸度的大小。

1.2.1 瓶頸指數(shù)的數(shù)學描述

文獻［18］從加工能力和加工需求兩個方面出發(fā)，以時間、質量和成本為參數(shù)，構建了瓶頸指數(shù)IBN的數(shù)學模型，其中，加工單元的瓶頸指數(shù)數(shù)學模型為

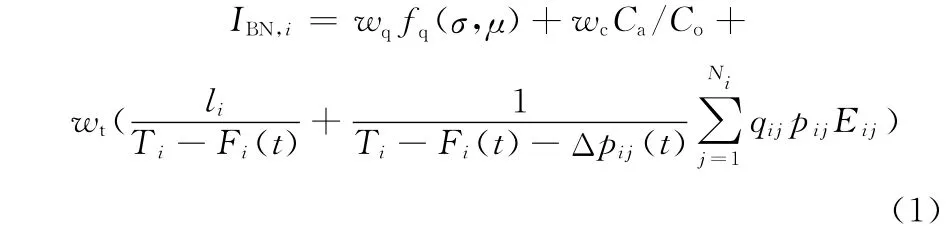
式中，wt、wq、wc分別為時間、質量和成本在瓶頸度中的影響權重，wt＋wq＋wc＝1；li、Ti分別為制造單元i的生產負荷與計劃可用生產時間；Fi（t）為制造單元i因實際生產條件變化而引起的生產能力變動量；pij、Eij、qij分別為產品j在制造單元i上的廢品率、單位處理時間、加工數(shù)量；Δpij（t）為j不合格品在制造單元i上的返修時間；Ni、fq（σ，μ）分別為制造單元i上加工產品的種類數(shù)和制造單元i質量保證能力對綜合瓶頸度的影響函數(shù)；σ、μ分別為質量特性的標準差和均值；Co、Ca分別為制造單元的目標成本和實際成本。

1.2.2 獨立瓶頸指數(shù)的數(shù)學描述

獨立瓶頸指數(shù)IBNI的數(shù)學模型可描述如下：

（1）若生產系統(tǒng)的零部件供應穩(wěn)定，則對于第一個制造單元，有IBNI，1＝IBN，1。

（2）當制造單元i與其前趨單元i－1在技術上無關聯(lián)時，IBNI，i＝IBN，i。

（3）當制造單元i與其前趨單元i－1在技術上相關聯(lián)時（兩制造單元均為加工單元），零部件的加工質量是2個制造單元相互影響的表征，前趨單元的制造成本和制造時間對后繼單元的影響通過零部件的質量加以反映。制造單元總質量由上影質量和分質量組成，其中，上影質量反映前趨單元對本制造單元的影響，分質量反映了本制造單元自身固有的加工能力和質量保證能力。因此，以瓶頸指數(shù)為基礎，以分質量和上影質量為輸入，構建獨立瓶頸指數(shù)的數(shù)學模型：

式中，IBNI，i為制造單元i的獨立瓶頸指數(shù)；β為消影系數(shù)，用以消除前趨單元i－1質量保證能力不足而引發(fā)i單元不合格率和生產成本的增加量，其大小與前趨單元i－1的質量保證能力及質量評定標準相關；fq（σ1，μ1）表示制造單元i的固有質量保證能力對其獨立瓶頸度的影響函數(shù)；σ1、μ1分別為分質量特性的標準差和均值。

制造單元i工序能力指數(shù)Cpk，i越高，產品質量穩(wěn)定性保證能力越高，對兩種瓶頸度的影響越小，其對應的權重wq也隨之越小。考慮質量的經(jīng)濟性，企業(yè)會根據(jù)客戶的需求，結合實際狀況設定適當?shù)脑u定標準。表1顯示了在一定評定標準下，消影系數(shù)β的確定方式；表2顯示了質量穩(wěn)定性保證能力對獨立瓶頸度的影響函數(shù)fq（σ1，μ1）和影響權重wq，其中，α1、α2、α3、α4為工序能力指數(shù)評價標準；Cpk1，i為第i道工序的分質量工序能力指數(shù)；θ∈ （0，1）；λ為變量，λ∈ （2，＋ ∞），Cpk，i－1越小，且離α4越近，λ越大。

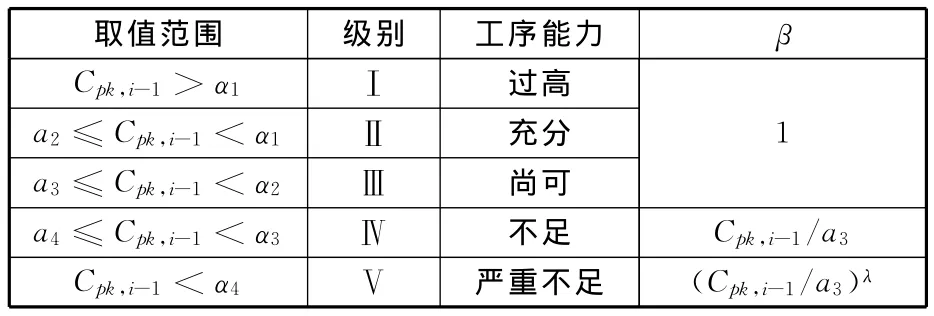
表1 消影系數(shù)β的確定規(guī)則

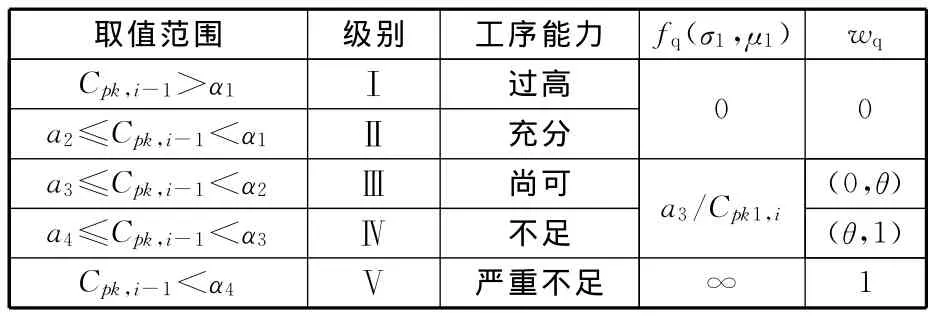
表2 fq（σ1，μ1）和wq 的確定

2 多瓶頸動態(tài)預測方法

以兩種瓶頸度為基礎，構建多瓶頸動態(tài)預測方法，其運作流程如圖1所示。圖1中，K為瓶頸個數(shù)。

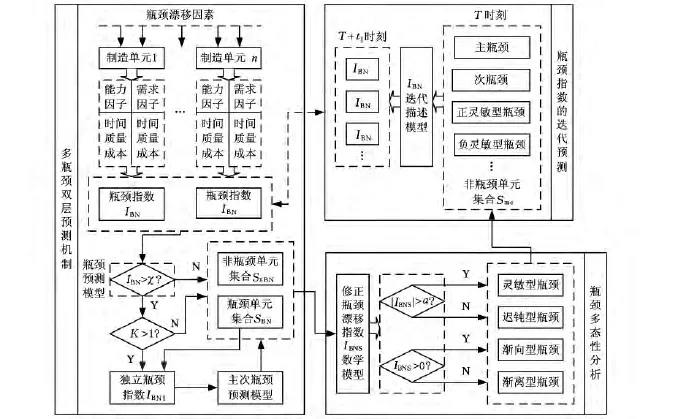
圖1 基于兩種瓶頸度的多瓶頸動態(tài)預測方法運作流程

由圖1可知，多瓶頸動態(tài)預測方法基本流程及內容如下：

（1）多瓶頸雙層預測機制。以瓶頸指數(shù)為依據(jù)，預測系統(tǒng)的瓶頸單元和非瓶頸單元。當系統(tǒng)存在多個瓶頸時，以獨立瓶頸指數(shù)為依據(jù)，實現(xiàn)主次瓶頸的預測。具體步驟如下：

步驟1 設定計劃期［0，T］，并將其分為l個時間段，表示為［t0，t1］，［t1，t2］，…，［tl－1，tl］，令t0＝0。

步驟2 統(tǒng)計分析計劃期［te－1，te］（e＝1，2，…，l）內制造單元i（i＝1，2，…，n）加工能力和加工需求相關的生產數(shù)據(jù)，具體包括制造單元可用加工時間、產品加工質量保證能力、單位產品目標成本、產品組合及各產品的工藝路線、已調度工件的執(zhí)行進度、單位產品處理時間及實際加工成本、質量需求等。

步驟3 計算［te－1，te］內制造單元i的瓶頸指數(shù)IBN，ie。

步驟4 計算［0，T］內制造單元i的瓶頸指數(shù)IBN，i＝ （0.5 IBN，i1＋ IBN，i2＋ …IBN，i（l－1）＋0.5IBN，il）／（l－1）。

步驟5 以瓶頸指數(shù)為指標，依據(jù)下式：

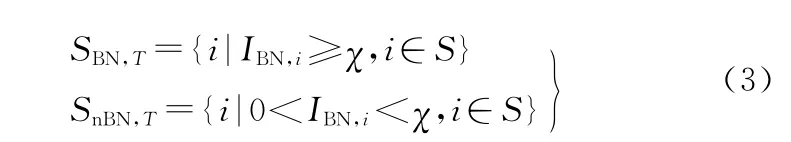
式中，SnBN，T、SBN，T為非瓶頸單元集合和瓶頸單元集 合；S為車間制造單元集合；χ為瓶頸判定標準，一般在0.9～1.0之間取值［16］。

預測系統(tǒng)在［0，T］內的瓶頸單元與非瓶頸單元。

步驟6 假設k為SBN，T元素個數(shù)，若k＞1，表示系統(tǒng)存在多個瓶頸，轉至步驟7；否則，預測結束。

步驟7 依據(jù)式（2），計算瓶頸單元r（r＝1，2，…，k）在［te－1，te］內的獨立瓶頸指數(shù)IBNI，ie，并最終計算其在［0，T］內的獨立瓶頸指數(shù)IBNI，i＝（0.5 IBNI，i1＋ IBNI，i2＋ … ＋ IBNI，i（k－1）＋0.5IBNI，ik）／（k－1）。

步驟8 依據(jù)式（4），預測系統(tǒng)的主瓶頸BF和次瓶頸BS：

（2）瓶頸多態(tài)性分析。在文獻［17］的基礎上，修正瓶頸漂移指數(shù)IBNS的數(shù)學模型，并依據(jù)瓶頸漂移指數(shù)大小，開展瓶頸多態(tài)性的分析，以識別系統(tǒng)的漸向型瓶頸、漸離型瓶頸、正靈敏型瓶頸和負靈敏型瓶頸。修正后的瓶頸漂移指數(shù)數(shù)學模型為

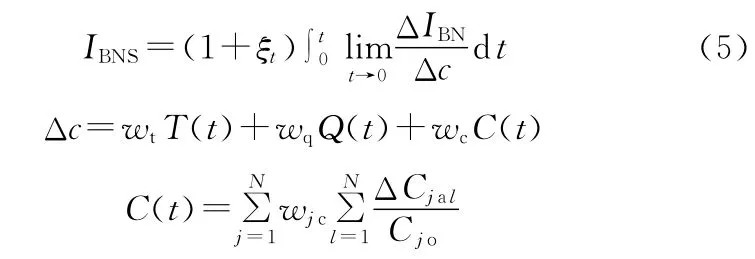
式中，ΔIBN為不確定性因素引發(fā)的制造單元瓶頸指數(shù)的變化量；Δc為各個不確定性因素對制造單元時間、質量和成本的綜合影響值；T（t）、Q（t）、C（t）分別為各因素在時間t內的變化對制造單元時間、質量和成本的影響；ξt為動態(tài)修正系數(shù)，以反映t時間內非隨機變量對制造單元的影響；ΔCjal為因素l的變化引起的制造單元上第j種產品的實際生產成本變化量；wjc為產品j實際成本變化幅度對C（t）的影響權重，根據(jù)各個產品計劃生產量占總生產量的比重進行設定。

（3）瓶頸指數(shù)的迭代預測［17］。以主瓶頸、次瓶頸、正靈敏型瓶頸、負靈敏型瓶頸、重點且具有正靈敏性的非瓶頸單元集合Smc在［0，T］內的瓶頸指數(shù)IBN，T為基礎，建立各個單元的瓶頸指數(shù)迭代預測模型：

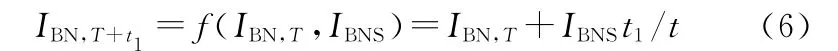
以預測各個單元在［T，T＋t1］時刻的瓶頸指數(shù)。

3 實例論證

以某汽車制造企業(yè)裝配車間中一產品總裝線為例，運用兩種瓶頸度動態(tài)預測法（dynamic prediction method based on two bottleneck degree，TBDM）、瓶頸指數(shù)法／單瓶頸度法（single bottleneck degree prediction method，SBDM）和基于最大出現(xiàn)頻率PBM預測方法（PBMM），預測該裝配線在22個生產日內的生產瓶頸，并采用文獻［6］中方法檢測實際瓶頸，以檢驗上述3類方法的準確性。該車間共有11個制造單元Mi（i＝1，2，…，11），其布局如圖2所示，裝配 A、B、C、D四類產品。表3顯示了各類產品每天的加工數(shù)量；表4表示各類產品的單位不確定處理時間；表5表示各類產品的單位目標成本co和實際成本ca，表6顯示了第1天制造單元加工產品時的質量保證能力，cp為工序能力指數(shù)，p為產品報廢率，返修產品在特定區(qū)域返修。

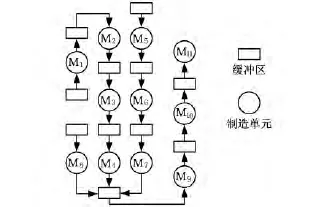
圖2 產品裝配總線布局

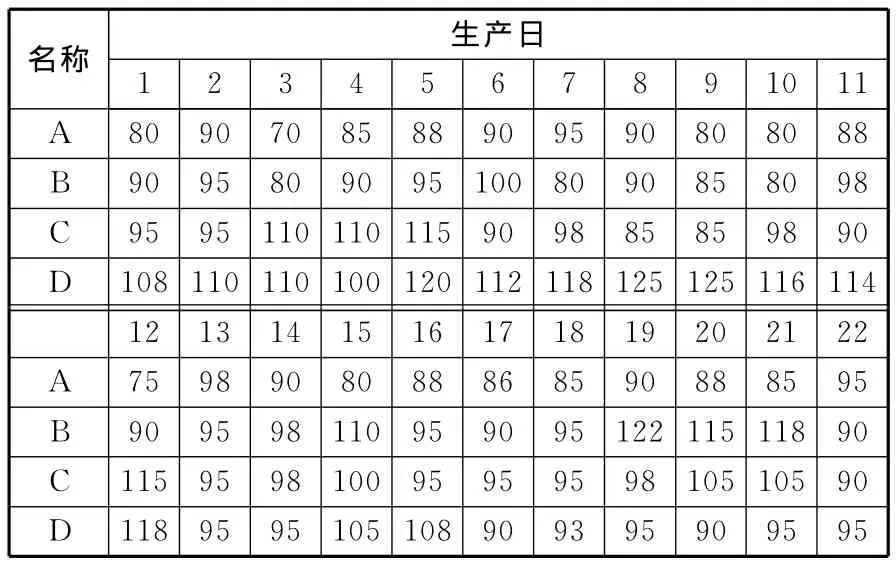
表3 產品加工數(shù)量 件

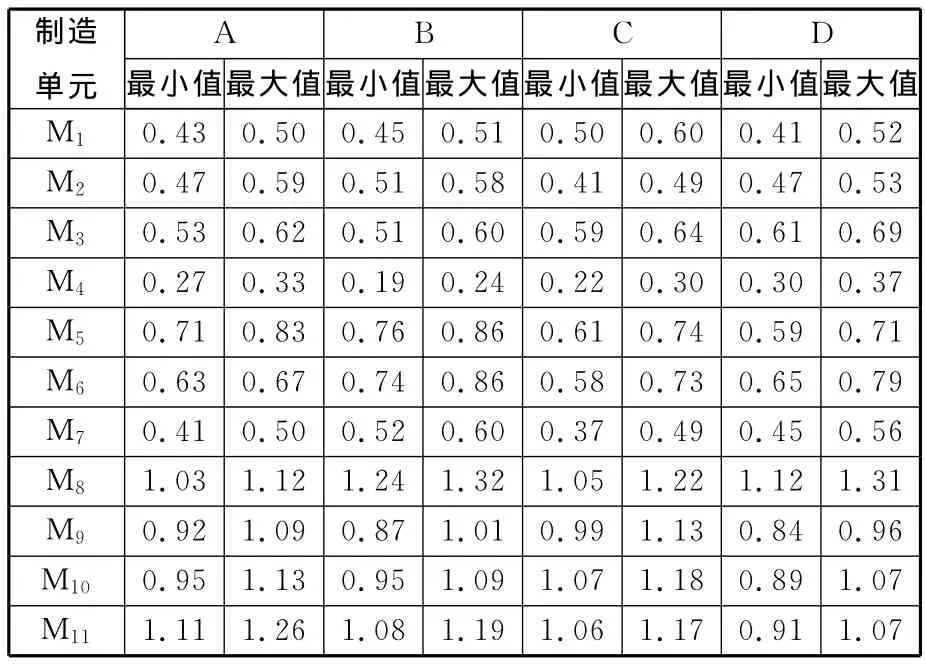
表4 單位產品的處理時間 min

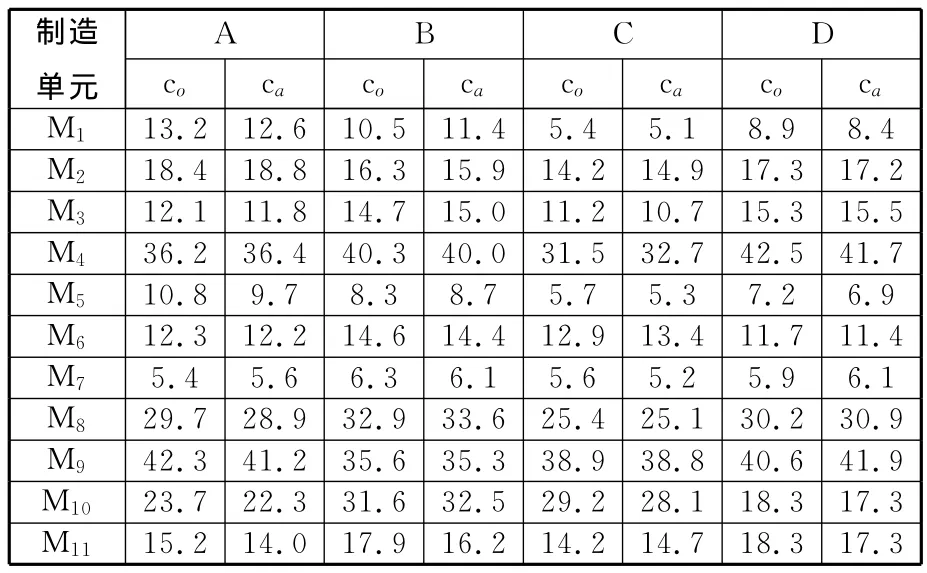
表5 單位產品的目標成本和實際成本 元

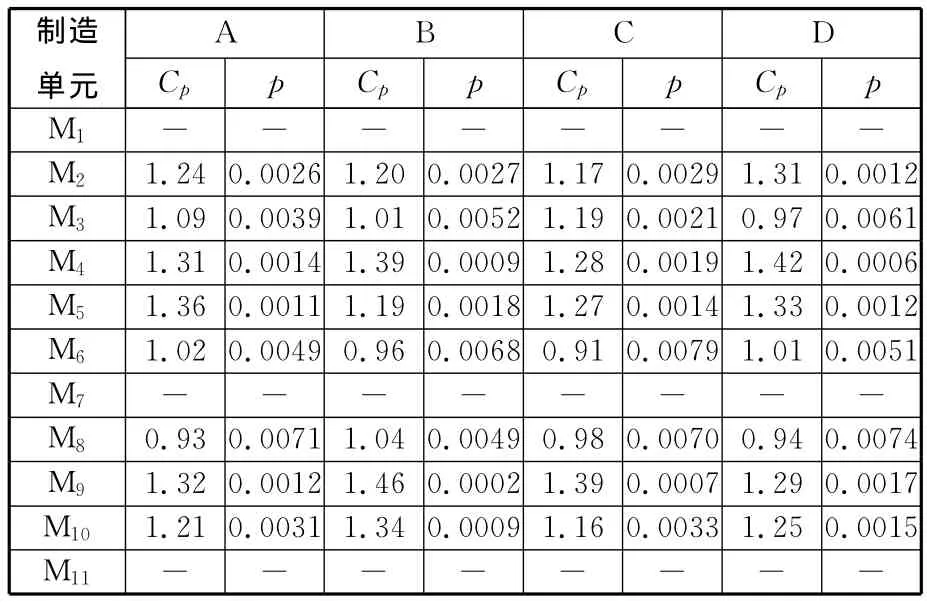
表6 制造單元質量保證能力

3.1 各方法的預測結果

計算各個制造單元在22個工作日內的瓶頸指數(shù)和非瓶頸指數(shù)，計算結果如表7、表8所示。22個工作日內制造單元M1～M5沒有獨立瓶頸指數(shù)IBNI，故在表8中，省略。利用TBDM、SBDM和PBMM預測系統(tǒng)瓶頸，結果如表9所示。其中，＊表示多瓶頸存在時，該瓶頸為主瓶頸。

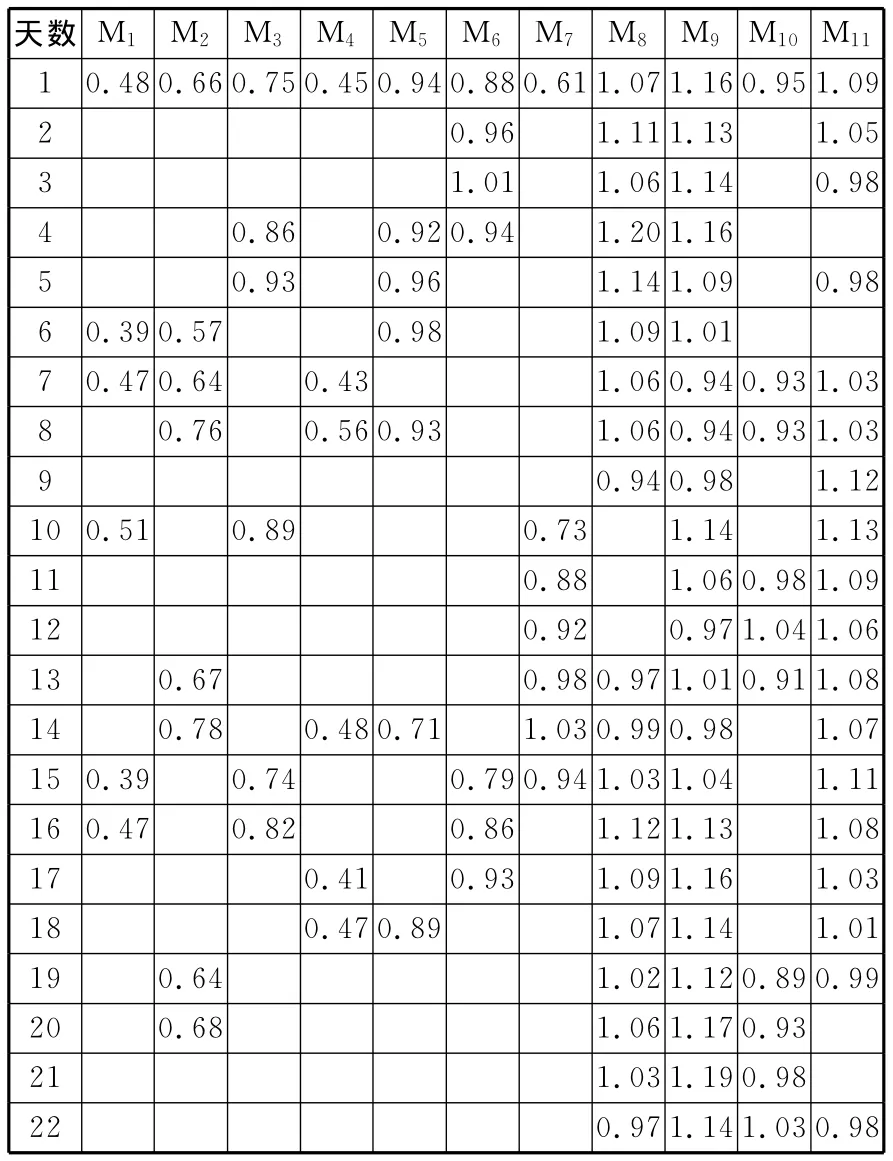
表7 各制造單元的瓶頸指數(shù)IBN計算結果

表8 各制造單元的獨立瓶頸指數(shù)IBNI計算結果（部分）

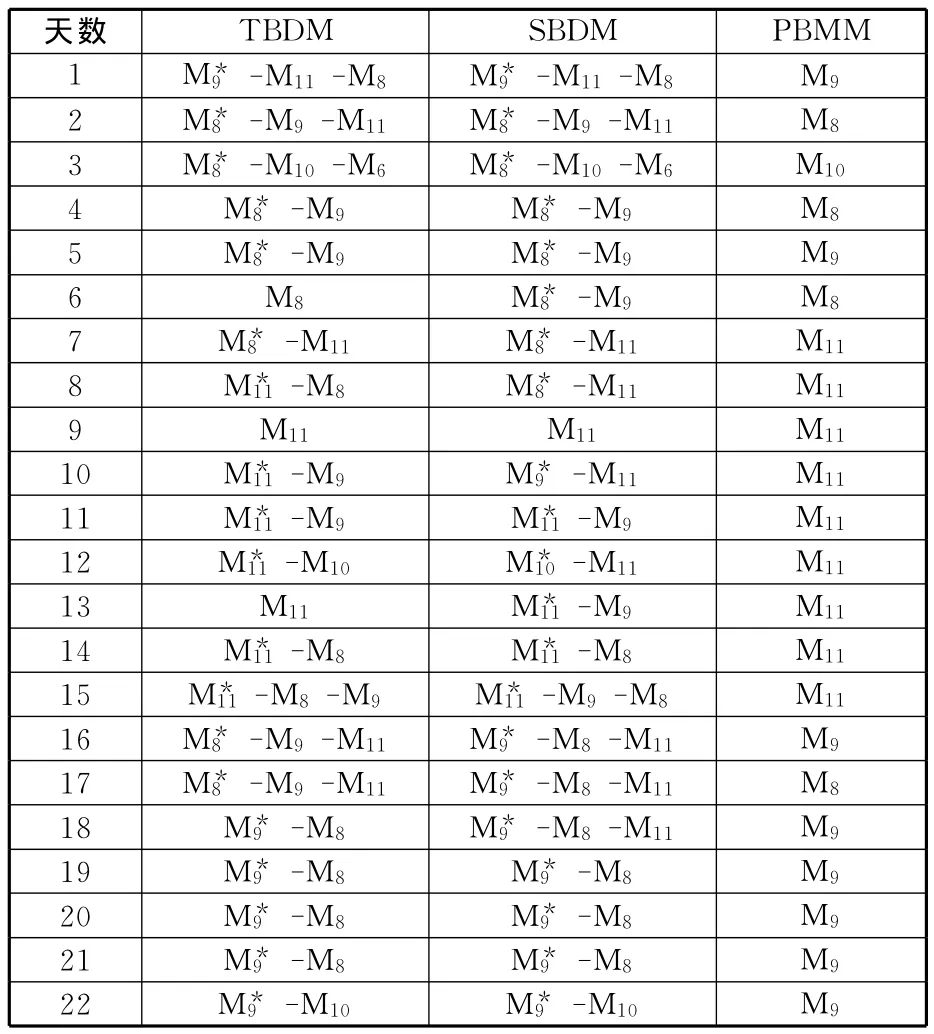
表9 瓶頸預測結果

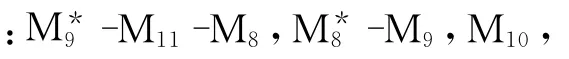
3.2 結果分析

（1）TBDM和SBDM在主瓶頸預測方面的吻合率為77.27%，次瓶頸預測結果的吻合率為63.64%，由此可知，兩者之間的預測結果并不總是一致，進而論證了制造單元的相關性對其后繼單元的瓶頸能力具有一定的影響。

（2）TBDM對主瓶頸、次瓶頸預測的準確率達到90.91%和81.82%，均高于SBDM（SBDM對主次瓶頸預測的準確率分別為77.27%和63.64%），由此可知，當制造單元間之間存在著較強的關聯(lián)性時，TBDM因合理認定瓶頸責任而使得瓶頸預測結果更加精確。

（3）PBMM 對主瓶頸預測的準確率為90.91%，與TBDM相同，但該方法只能預測出系統(tǒng)的主瓶頸，對其他非主瓶頸則忽略不計，使得不確定性環(huán)境下生產過程優(yōu)化決策因未考慮多瓶頸相互關系而降低柔性。

4 結語

針對現(xiàn)有瓶頸預測方法存在的不足，本文提出了基于兩種瓶頸度的多瓶頸動態(tài)預測方法。基于兩種瓶頸度構建的包含多瓶頸雙層預測機制、瓶頸多態(tài)性分析和瓶頸指數(shù)迭代預測的動態(tài)預測方法，在合理區(qū)分瓶頸責任、定量描述瓶頸漂移過程和保證瓶頸預測精度的前提下，實現(xiàn)了系統(tǒng)瓶頸預測由間斷轉向連續(xù)，為生產過程的合理規(guī)劃和有效控制提供了依據(jù)。

［1］韓文民，葉濤鋒.混流條件下基于TOC制定生產作業(yè)計劃的關鍵問題：研究現(xiàn)狀及發(fā)展探討［J］.江蘇科技大學學報，2005，19（6）：92－96.Han Wenmin，Ye Taofeng.Critical Problems on Determining Production Scheduling for Hybrid Flow Shop Based on TOC：A Survey［J］.Journal of Jiangsu University of Science and Technology，2005，19（6）：92－96.

［2］李黎，成曄，袁守華.基于瓶頸分析的優(yōu)先權調度算法研究［J］.計算機集成制造系統(tǒng)－CIMS，2005，12（11）：247－250.Li Li，Cheng Ye，Yuan Shouhua.Research on Priority Scheduling Algorithm Based on Bottleneck Analysis［J］.Computer Integrated Manufacturing Systems，2005，12（11）：247－250.

［3］Ching S N，Meerkov S M，Zhang Liang.Assembly Systems with Non－exponential Machines：Throughput and Bottlenecks［J］.Nonlinear Analysis，2008，69：911－917.

［4］Li Lin，Chang Qing，Ni Jun.Data－driven Bottleneck Detection of Manufacturing Systems［J］.International Journal of Production Research，2009，47（18）：5019－5036.

［5］Yan Hongsen，An Yuwei，Shi Wenwu.A New Bottleneck Detecting Approach to Productivity Improvement of Knowledgeable Manufacturing System［J］.Journal of Intelligent Manufacturing，2010，21（6）：665－680.

［6］Roser C，Nakano M，Tanak M.Comparison of Bottleneck Detection Methods for AGV Systems［C］／／Proceedings of the 2003Winter Simulation Conference.New Orleans，2003：1192－1198.

［7］Faget P，Eriksson U，Herrmana F.Applying Discrete Event Simulation and an Automated Bottleneck Analysis as an Aid to Detect Running Production Constraints［C］／／Proceedings of the 2005Winter Simulation Conference.Orlando，2005：1401－1407.

［8］Rajakumar S，Arunachalam V P，Selladuraiv V.Workflow Balancing in Parallel Machine Scheduling with Precedence Constraints Using Genetic Algorithm［J］.Journal of Manufacturing Technology Management，2006，17（2）：239－254.

［9］張懷，江志斌，郭乘濤.面向瓶頸的半導體晶圓制造系統(tǒng)派工策略及參數(shù)優(yōu)化［J］.上海交通大學學報，2007，41（8）：1252－1257.Zhang Huai，Jiang Zhibin，Guo Chengtao.The Bottleneck－oriented Dispatching Strategy and Parameter Optimization in Semiconductor Wafer Fabrication System［J］.Journal of Shanghai Jiaotong University，2007，41（8）：1252－1257.

［10］翟穎妮，孫樹棟，王軍強，等.基于正交試驗的作業(yè)車間瓶頸識別方法［J］.計算機集成制造系統(tǒng)，2010，16（9）：1945－1952.Zhai Yinni，Sun Shudong，Wang Junqiang，et al.Bottleneck Detection Method Based on Orthogonal Experiment for Job Shop［J］.Computer Integrated Manufacturing Systems，2010，16（9）：1945－1952.

［11］王剛，王軍強，孫樹棟，等.擾動環(huán)境下Job Shop瓶頸識別方法研究［J］.機械科學與技術，2010，29（12）：1697－1702.Wang Gang，Wang Junqiang，Sun Shudong，et al.Machine Bottleneck Identification for Job Shop Operation Management［J］.Mechanical Science and Technology for Aerospace Engineering，2010，29 （12）：1697－1702.

［12］Zhang Rui，Wu Cheng.Bottleneck Identification Procedures for the Job Shop Scheduling Problem with Applications to Genetic Algorithms［J］.The International Journal of Advanced Manufacturing Technology，2009，42（11）：1153－1164.

［13］Zhang Rui，Wu Cheng.Bottleneck Machine Identification Method Based on Constraint Transformation for Job Shop Scheduling with Genetic Algorithms［J］.Information Sciences，2012，188：236－252.

［14］Singh R K，Prakash K S，Tiwari M K.Psycho－clonal Based Approach to Solve a TOC Product Mix Decision Problem［J］.International Journal of Advanced Manufacturing Technology，2006，29（11／12）：1194－1202.

［15］Richard A R.Applying the TOC Five－step Focusing Process on the Service Sector－A Banking Subsystem［J］.Managing Service Quality，2007，17（2）：209－234.

［16］Liu Mingzhou，Tang Jun，Ge Maogen，et al.Dynamic Prediction Method of Production Logistics Bottleneck Based on Bottleneck Index［J］.Chinese Journal of Mechanical Engineering，2009，22（5）：710－716.

［17］劉志，唐娟，費志敏.基于瓶頸多態(tài)性的生產物流瓶頸閉環(huán)預測方法［J］.計算機集成制造系統(tǒng)，2012，18（11）：2554－2561.Liu Zhi，Tang Juan，F(xiàn)ei Zhimin.Close－loop Prediction Method of Logistics Bottleneck Based on Bottleneck Polymorphism ［J］.Computer Integrated Manufacturing Systems，2012，18（11）：2554－2561.

［18］唐娟，劉志.基于瓶頸指數(shù)的生產物流瓶頸多態(tài)性研究［J］.現(xiàn)代制造工程，2011（10）：23－26.Tang Jun，Liu Zhi.Research on Polymorphism of Production Logistics Bottleneck Based on Bottleneck Index［J］.Modern Manufacturing Engineering，2011（10）：23－26.