機械碰撞振動系統分岔與混沌的參數演化

柴 林，吳曉明

（廈門大學物理與機電工程學院，福建 廈門361005）

碰撞振動是機械系統中常見的一種現象，其響應可能會呈現復雜的非線性混沌現象.在工程實際中，一方面，為了某種生產目的，可以利用碰撞振動的動力學原理設計制造如振動篩、壓路機、微振造型機等多種沖擊振動機械；另一方面，碰撞振動也可能造成負面影響，如降低穩定性、損壞設備、制造噪聲等，特別是碰撞振動所產生的非線性運動是造成機械部件疲勞、損壞的主要原因之一［1］.因此，工程實際中要根據機械系統的功能需求去選擇利用或者避免碰撞振動的非線性動力學現象.

碰撞振動是一個復雜的過程，它受多方面因素的影響，如碰撞體的約束狀況、接觸時的相對速度、接觸面的幾何形狀及接觸持續時間、局部塑性變形等，其研究涉及工程機械、系統動力學、數值分析等多個專業領域.牛頓、Poisson及 Whittaker理論構成了經典碰撞動力學理論的框架.在系統進行動態分析時，用于描述碰撞過程的模型有3種［2－3］：1）瞬時沖擊模型；2）分段線性模型；3）考慮碰撞中的局部變形的模型，用Hertz接觸理論描述接觸力.

本文以一大類實際工程機械，如振動篩、制磚機、振動壓實機為基礎，建立了單自由度碰撞振動機械的通用動力學模型.采用瞬時沖擊法，在碰撞過程中只考慮能量的損失，利用恢復系數法計算碰撞前后速度之間的關系，用四階龍格——庫塔法求解模型的動力學微分方程，討論設計參數變化時系統呈現周期運動以及混沌現象的演化過程.

1 動力學模型及其運動方程

具有約束的單自由度碰撞振動系統的動力學模型如圖1所示，質量為m的振子由剛度為k／2的線性彈簧和阻尼系數為c／2的阻尼器對稱連接于支承臺，振動臺質量為M并受到振幅為A、頻率為ω的強制簡諧激勵的作用，碰撞恢復系數設為R.

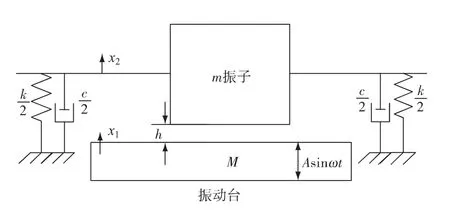
圖1 單自由度碰撞振動系統的力學模型Fig.1 Mechanics model of SDOF collision vibration system

系統在未發生碰撞時，自由運動階段方程為：

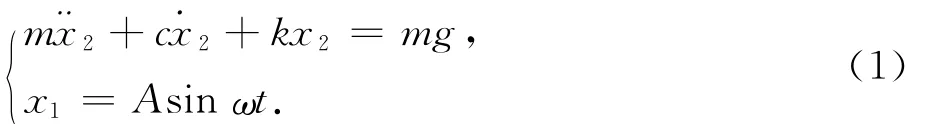
碰撞過程采用瞬時沖擊模型，“－”、“＋”分別表示振動臺與振子碰撞前后的瞬時狀態，碰撞前后瞬時速度關系式為［4］：

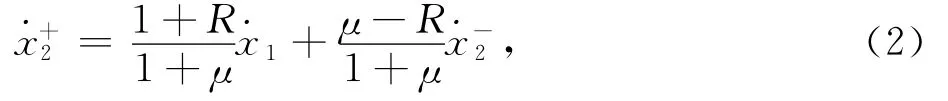
在MATLAB中用四階龍格－庫塔法求解二階微分方程，并判斷當x1＝x2時即發生碰撞，分別把這一時刻的速度值˙x－2和˙x1帶入式（2）中，求出瞬時碰撞后下一時刻的速度.計算時，步長設置為ts＝0.000 1s，運行時間為4s.

已知參數有：m＝200kg，c＝11 000N·s／m，k＝500 000N／m，g＝10m／s2，A＝0.05m，h＝0.02m，R＝0.9，μ＝0.1，ω＝50×2π＝314.16rad／s，x2為位移，單位：m；dx2為速度，單位：m／s.

MATLAB運行結果如圖2所示.從圖2（a）、（b）可以看出振子作復雜的非周期運動，每一次碰撞結束后的一周期內速度和位移均無規律可言.由圖2（c）可以看出，從相圖得到運動狀態是由多條不封閉曲線組成，而圖2（d）上分布著多個離散的無規律的點，說明系統出現了混沌現象［5］.

2 參數對系統響應狀態的影響

對于碰撞振動系統，設計參數的變化對系統是周期性響應還是混沌狀態具有決定性影響，本節討論碰撞振動系統設計參數對系統響應狀態的影響.

圖2 系統動態響應Fig.2 Dynamics responses of system

2.1 初始碰撞位置

系統參數如上節所述，分別取初始碰撞位置h＝0.04m和h＝0.003m，數值仿真的位移和相圖如圖3所示，結合圖2所示h＝0.02m時的系統響應圖，可以看出系統運動狀態表現出隨機性和不可預測性，但同時振子的最大位移和整體運動趨勢局限在一定范圍內，顯現出局部不穩定而整體穩定的特性［6－7］.在碰撞間隙為0～0.05m的范圍內取值為0.003，0.02和0.04m的仿真數值結果表明，系統運動狀態變化不大，碰撞間隙作為參數對系統的混沌現象產生和演化影響并不明顯.

2.2 黏性阻尼系數

以阻尼系數為分岔參數，數值仿真系統的運動狀態.通過計算，得到阻尼從4 000～18 000N·s／m，振子的狀態變量全局分岔圖（見圖4），圖中位置“一、二、三”分別對應參數阻尼c的值為9 280，10 290，11 610N·s／m.從圖中可見，振子在“一”位置進入周期倍化階段，此后系統從倍化分岔序列通向混沌，在“二”位置進入混沌運動狀態，在“三”位置結束混沌運動狀態.為此，我們分別選取c為10 000，10 500和16 000N·s／m進行動態響應數值計算，結果如圖5所示.

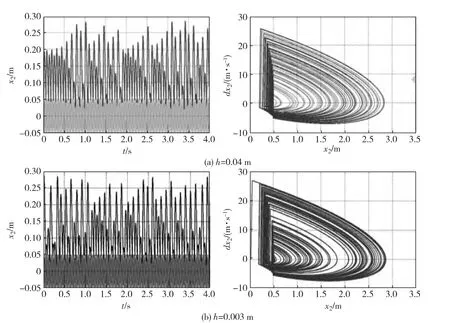
圖3 不同初始碰撞位置的位移響應圖（左）和相圖（右）Fig.3 Displacement－velocity response graph（left）and phase portraits（right）（h＝0.04m、h＝0.003m）

圖4 阻尼c的全局分岔圖Fig.4 Overall bifurcation of damp

從圖5可看出，在阻尼c分別取10 000，10 500 N·s／m時，系統處于周期倍化運動狀態和混沌狀態.當阻尼c＝16 000N·s／m時，相圖是一條閉合曲線，Poincaré截面映射圖上表現為孤立的1個點，說明振子的響應呈現周期性，系統具有穩定的周期運動.

由阻尼變量全局分岔圖4可見，碰撞振動系統的運動狀態對振子支撐元件阻尼參數是敏感的，特別是在運動響應隨阻尼變化發生分岔進而出現混沌狀態的交界點“一”“二”“三”位置附近，阻尼常數的小變化會引起系統運動的極大變化.

2.3 剛度k

選定一組基本參數c＝6 000N·s／m，m＝200kg，A＝0.05m，ω＝314.16rad／s，取剛度k為變化參數，數值計算出關于參數k的全局和局部分岔圖，如圖6所示.

可見，剛度對系統響應周期的影響極大.隨剛度增加，系統的運動狀態變得復雜，混沌運動與周期運動、擬周期交錯出現.從圖6可看出，當k的數值從0.85×106N／m遞增到0.95×106N／m 時，運動軌跡和周期性變得更為豐富，系統分別經歷突變、倍化分岔、臨界hopf分岔連接混沌區域.

2.4 激振頻率ω

選定一組基本參數為m＝200kg，A＝0.05m，k＝500 000N／m，取激振頻率ω為變化參數，計算出ω的系統全局分岔圖，如圖7所示.

從圖7可得出，當阻尼系數一定時，隨激振頻率增加，振子的周期運動與非周期運動交替出現，且相鄰周期與非周期的運動狀態組合呈現一定規律性，并可看出周期運動和混沌區域的最高點逐漸增加；而隨著阻尼系數c的遞增，系統振子運動的最高位置明顯減小，周期運動與混沌界限變得模糊，混沌區域增加.

圖5 不同阻尼c的系統動態相應數值仿真計算結果Fig.5 Displacement－velocity response and Phase portraits

圖6 剛度k的全局和局部分岔圖Fig.6 Overall and part bifurcation of stiffness

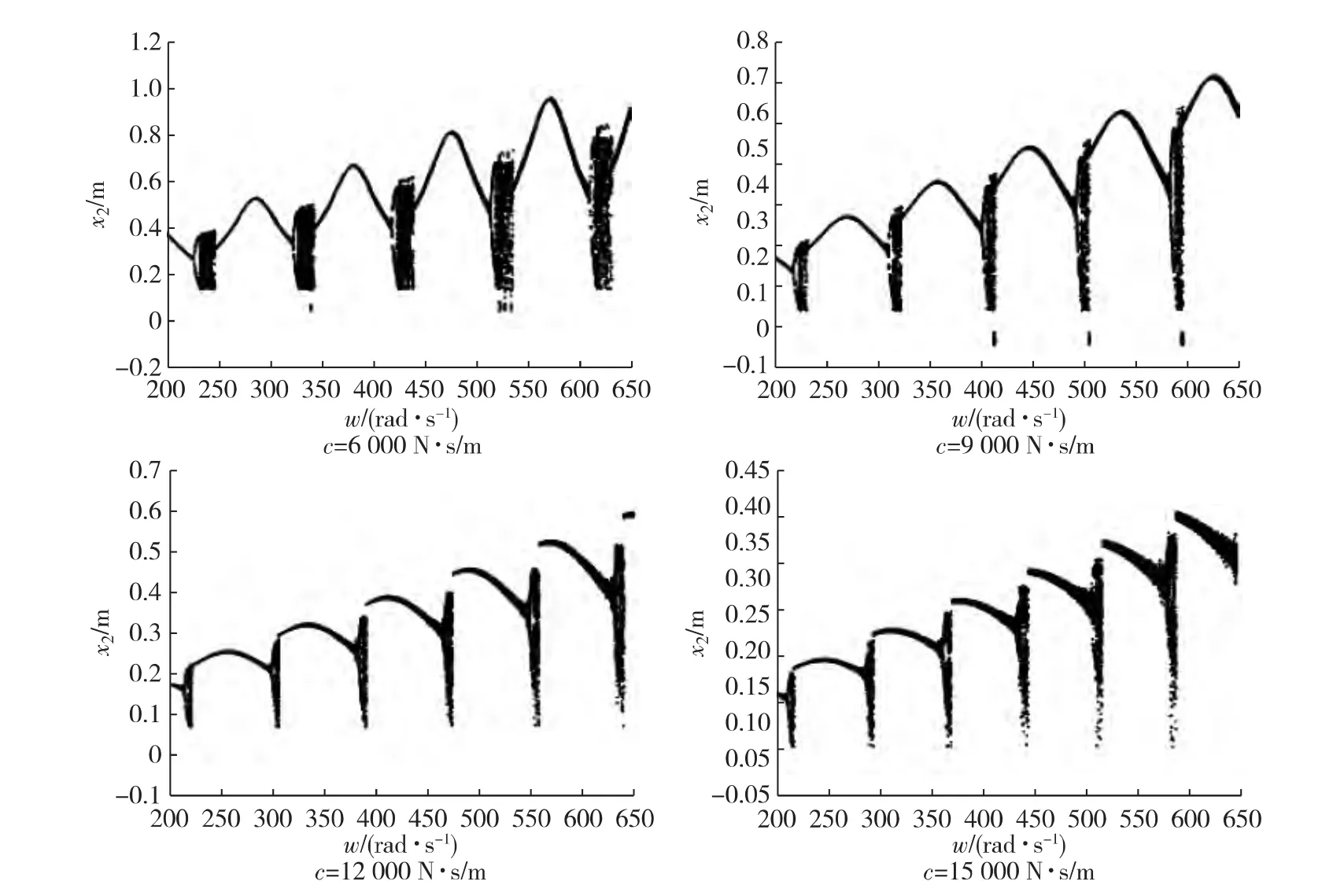
圖7 頻率ω的全局分岔圖Fig.7 Overall bifurcation of frequency

3 典型設計參數的三維全局分岔圖

系統分岔圖是實際機械系統中設計參數選取的重要依據［8］.而典型設計參數往往是多元的，以臺式制磚機為例，為了使振子運動達到理想工作狀態，最常用的方法是改變支撐振子的彈簧和阻尼.由于二維分岔圖每次只能選取單個設計參數，然后進行反復地樣機試制實驗，準確找到所需要的彈簧剛度和阻尼參數值并非易事.本文對力學模型的剛度和阻尼兩個參數變化進行數值計算，得到系統剛度和阻尼在一定區間內變化的三維全局分岔圖.

從圖8可以得到，當阻尼c取6 000～14 000 N·s／m、剛度k從4.6×105N／m 遞增到5.4×105N／m的區間中，振子在穩定單周期運動時位移最高點逐漸增大，而混沌區域逐漸減小，剛度k取4.6×105N／m時的系統混沌面積是取5.4×105N／m時的3倍左右.

4 結 論

圖8 分岔三維圖Fig.8 Three－dimensional bifurcation

針對含間隙碰撞振動系統，建立了其力學模型，研究了設計參數變化所引起的系統動力學響應從平衡狀態到出現分岔及混沌現象的演變過程.通過設計參數包括初始碰撞位置、黏性阻尼因子、剛度和振動臺激振頻率的變化，得到可以反映系統運動狀態的時間歷程圖、相圖、分岔圖和Poincaré截面圖，全面反映系統周期運動和混沌運動狀態的演化過程.根據機械設計參數多元化的特點，提出了兩個典型參數變化過程的三維分岔圖，為含間隙的碰撞振動機械系統的參數設計提供理論依據.

［1］丁旺才，謝建華.碰撞振動系統分岔與混沌的研究進展［J］.力學進展，2005，35（4）：513－524.

［2］金棟平，胡海巖.碰撞振動與控制［M］.北京：科學出版社，2005.

［3］Peterka F，Tondl A.Phenomena of subharmonic motions of oscillator with soft impact［J］.Chaos，Solutions ＆Fractals，2004，19（5）：1283－1290.

［4］丁旺才，謝建華，李萬祥.碰撞振動系統強共振下的兩參數動力學分析［J］.計算力學學報，2004，21（6）：658－664.

［5］楊尚普.含非線性彈簧－阻尼碰撞振動系統的動力學研究［D］.蘭州：蘭州交通大學，2012.

［6］聞邦椿，李以農，徐培民，等.工程非線性振動［M］.北京：科學出版社，2007.

［7］陳予恕.非線性振動［M］.北京：高等教育出版社，2002.

［8］魏艷輝.一類兩自由度碰撞振動系統的動力學研究［D］.桂林：廣西大學，2007.