被動雷達導引頭抗干擾性能評估指標權重算法＊

張平峰 孟 蕾 肖 韓

（1.海軍駐上海某軍事代表室 上海 200000）（2.海軍航空工程學院 煙臺 264001）（3.91867部隊41分隊 義烏 322000）

1 引言

被動雷達導引頭具有探測距離遠、隱蔽性好、耗能少等優點，已經被廣泛用于反輻射導彈［1］和防空導彈［2］。現代海上復雜戰場干擾環境下，其抗干擾性能評估顯得越來越重要［3～5］。抗干擾指標不是都可以量化，有一部分指標只能進行定性分析，所以必須通過定量和定性相結合的方法來綜合評價導引頭的抗干擾能力，考慮到抗干擾指標的多層次性和評估的模糊性，本文選用模糊層次分析法建立被動雷達導引頭抗干擾能力指標體系［6～8］。

2 基于自信度的專家打分法

傳統的專家打分法只要求專家對各因素之間的相對重要性打分。由于評估問題量化的復雜性，專家的打分往往存在一些不確定的主觀因素。為了描述這種不確定性，可以請專家給相對重要性打分的同時，也對自己打分時的自信度做合理的估計，同樣也以打分的形式給出，這個自信度可以用重要性比值的均方差來具體量化，這種打分法是把相對重要性比值看作是有一定波動范圍的隨機變量。專家對每一對指標評估時要給出兩個分值，一個代表重要性比值的大小，另一個代表自信度的大小，打分的分值在1～9之間。

提出層次分析法的美國運籌學家T.L.Saaty最早采用的1～9標度法對打分進行賦值，后人對標度法進行了改進，根據韋伯—費希納準則，人的主觀感覺等差遞增時，刺激感覺的客觀物理量是等比遞增的，所以指數標度法更符合人們的認知規律，專家對重要性程度和自信度的打分含義如表1所示，表中同時給出了打分分值相對應的指數標度值。

表1 專家打分的含義

假設相對重要性比值X近似服從正態分布，即X～N（β，δ2），X的概率密度函數可以表示為

由于正態分布的隨機變量基本分布在均值β的3δ范圍內，根據以上分析可知，專家對指標的相對重要性進行評估時給出的不再是單一數值，而是根據自己的經驗給出的一個數集（β－3δ，β＋3δ），在這個集合內fX（x）的積分幾乎等于1，重要性比值不會接近0，而δ一般很小，所以在β－3δ＞0時，有

假設專家對重要性比值X的打分分值為k，對自信度δ0的打分分值為t，標度計算公式為

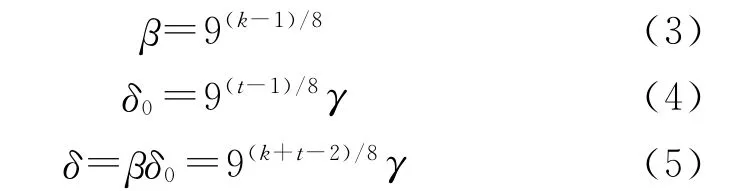
式中，β為X的均值，δ為X 的均方差。自信度δ0可以認為是X的均方差δ與均值β的比值，也就是X的相對誤差，δ0越大表示X的波動范圍越大，此時專家對自己的判斷自信性也越小，相反，δ0越小表示X的波動范圍越小，專家對自己的判斷自信性也越大。γ為對自信度打1分時δ0的大小，專家自信性最差時打9分，δ0＝9γ，此時X大部分分布在β（1±27γ）范圍內，考慮到專家自信性最差時允許X的波動范圍在30%以內，γ可取值1%。

被動雷達導引頭的抗干擾指標主要有抗有源噪聲干擾和欺騙干擾指標，無源干擾對被動雷達作用不大。抗有源噪聲干擾指標主要有測角精度、跟蹤精度、壓制系數和相對燒穿距離。抗欺騙干擾指標主要有抗欺騙干擾概率和抗誘偏瞄準誤差。針對被動雷達導引頭識別目標所采取的若干抗干擾措施，識別能力指標有識別概率，載頻、重頻和脈寬可識別范圍，抗頻率捷變范圍等。被動雷達導引頭抗干擾指標體系如圖1所示。

圖1 被動雷達導引頭抗干擾指標體系

以被動雷達導引頭抗有源噪聲干擾指標下層的四個指標為例，專家打分表如表2所示，相對重要性只需要兩兩進行比較，所以四個指標的相對重要性比值有C24個，n個指標的重要性比值有C2n個，兩兩比較時順序不同的相對重要性比值互為倒數，所以只需要知道其中一個就行，為了方便標度，專家只需要給出大于1的比值，同時在表中注明比較的順序。

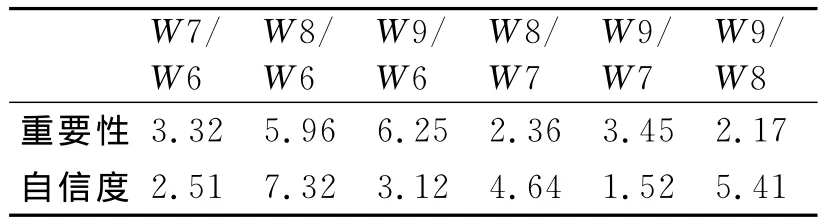
表2 專家對W6～W9指標的打分表

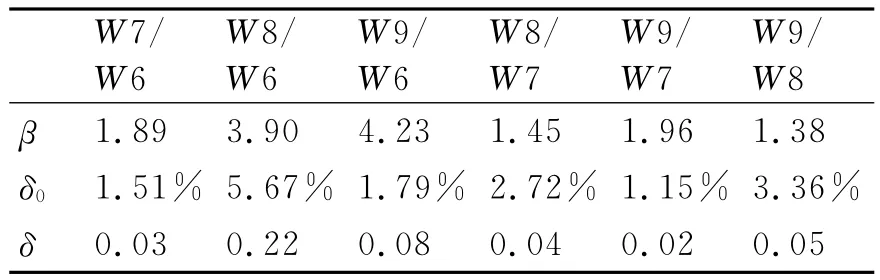
表3 X的均值和均方差計算表

表中，專家對W7／W6的重要性打分k＝3.32，對自信度打分t＝2.51，表明這位專家認為W7指標比W6指標稍微重要，并且對自己判斷非常有自信。k＝3.32對應的重要性比值的均值β＝1.89，t＝2.5對應的自信度是δ0＝1.51%，重要性比值的均方差δ＝βδ0＝0.029。同樣方法可以得到其它重要性比值的均值β、自信度δ0和均方差δ，專家打分表經過指數標度法處理后得到表3。

重要性比值X＝W7／W6的概率密度函數為f76（y），類似的有f86（y），f96（y），f87（y），f97（y），f98（y），它們的圖像如圖2所示。

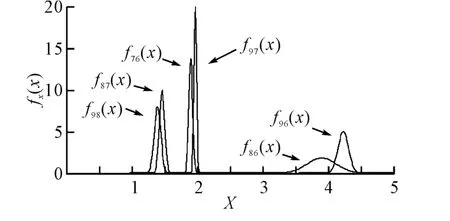
圖2 X概率密度函數

為了更加客觀地評價，專家往往不止一個，若總共有m個專家參加打分，他們對某一對指標的打分處理結果為（β1，δ1），（β2，δ2），…，（βm，δm），按照正態分布隨機變量疊加理論，m個專家的評價綜合結果為（β，δ）

3 構造判斷矩陣

對專家打分的指數標度實際上只是給出了判斷矩陣中非對角線元素中的一半，即兩兩比較時，只給出了其中大于1的比值，而且這個比值是個隨機變量X，當這兩個元素位置顛倒過來時，重要性比值是小于1的，這時重要性比值也是個隨機變量Y［9］。構造判斷矩陣時，需要由X計算相應的Y，設X的分布函數和概率密度函數分別為FX（x）和fX（x），Y的分布函數和概率密度函數分別為FY（y）和f′Y（y），并且有Y＝1／X。在 X 近似服從正態分布的假設下，X和Y的散布范圍都很小，為負數的可能性極小，即可以認為FX（0）＝FY（0）＝0，x，y＞0，計算Y的概率密度函數

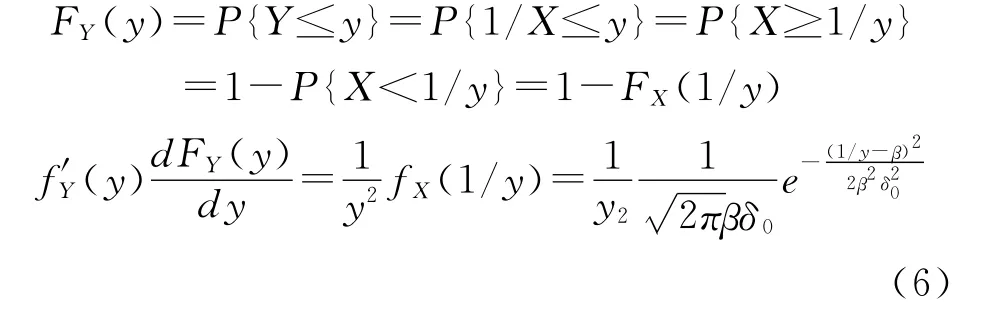
下面驗證f′Y（y）的積分是否為1：

做變量代換，x＝1／y，由式（2）知

明顯隨機變量Y的分布不屬于正態分布，f′Y（y）的形式和逆高斯分布類似

在λ趨于無窮大時，逆高斯分布逐漸趨近于高斯分布，可以設想一定條件下Y也是近似服從正態分布的。為了統一判斷矩陣中各個元素的分布情況，可以假設小于1的重要性比值Y也是符合正態分布的，并且Y的相對誤差σ0和對應的大于1的重要性比值X的相對誤差δ0是相同的，即σ0＝δ0，這樣就避免了通過隨機變量X的分布求隨機變量Y的分布，結果不為正態分布的困難局面。根據假設Y～N（α，σ2），則有

下面證明，y在1／β附近，即當y－1／β≈0時，有f′Y（y）≈fY（y），將式（6）和式（10）中的指數部分分別展開成泰勒級數：

當δ0≤0.1的時候，由y≈1／β知1／β－y2β≈0，式（11）分子減去分母得

所以，可得出結論：在δ0≤0.1的情況下，當X服從正態分布時，Y也是近似服從正態分布的。β＝2，自信度δ0取不同值時，概率密度函數f′Y（y）和fY（y）的圖像如圖3所示。

從圖2中可以看f′Y（y）和fY（y）的圖像非常相似，尤其是當相對誤差δ0≤0.1時，這說明通過Y＝1／X由X 求得Y的分布情況和通過X、Y有相同相對誤差σ0＝δ0求得的結果幾乎是相同的，這兩種方法并不沖突。

圖3 兩種概率密度函數

考慮到后期對判斷矩陣進行數據處理的方便性，選用第二種方法，經計算可以得到小于1的重要性比值的均值α、自信度σ0和均方差σ，如表4所示。

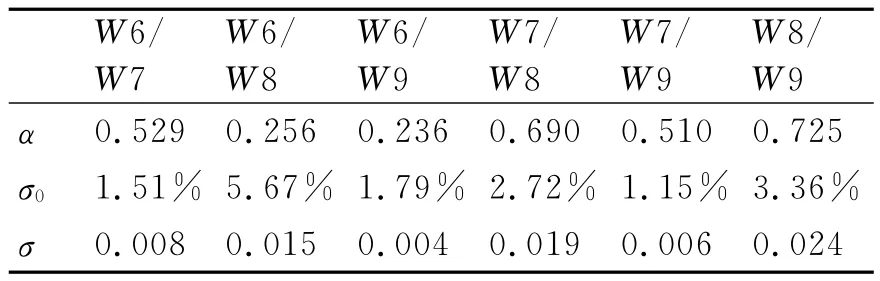
表4 Y的均值和均方差計算表

重要性比值Y＝W6／W7的概率密度函數為f67（y），類似的有f68（y），f69（y），f78（y），f79（y），f89（y），它們的圖像如圖4所示。

圖4 Y的概率密度函數

這樣可以認為判斷矩陣中所有的元素都屬于變化范圍較小的正態隨機變量，所以每個元素需要有兩個參數才能完整描述，即均值和均方差。W6～W9指標的判斷矩陣如表5所示。

表5 W6～W9指標的判斷矩陣

4 計算指標權重

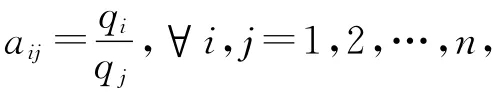
n階正互反矩陣A為一致矩陣當且僅當其最大特征根λmax＝n，且當正互反矩陣A非一致時，必有λmax＞n。可以由λmax是否等于n來檢驗判斷矩陣A是否為一致矩陣。當λmax比n大得越多，A的非一致性程度也就越嚴重，λmax對應的標準化特征向量也就越不能真實地反映各指標所占的比重。因此，對判斷矩陣有必要作一次一致性檢驗，以決定是否能接受它。對判斷矩陣的一致性檢驗的步驟如下：

第一步，計算一致性指標CI

第二步，查找相應的平均隨機一致性指標RI。對n＝1，…，9，指數標度法RI的值如表6所示。

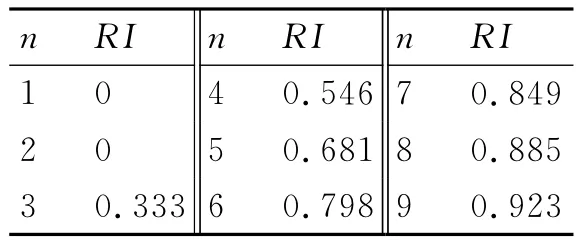
表6 指數標度法RI的值

指數標度法的平均隨機一致性指標RI是這樣得到的，用隨機方法構造500個樣本矩陣：隨機地從9－8／8，…，9－1／8，1，91／8，…，98／8共17個數中抽取數字構造正互反矩陣，求得最大特征根的平均值λ′max，并定義

第三步，計算一致性比例CR

當CR＜0.10時，認為判斷矩陣的一致性是可以接受的，否則應對判斷矩陣作適當修正。若有判斷矩陣A＝（aij）n×n，定義矩陣C＝（cij）n×n滿足

則稱C為判斷矩陣A的導出矩陣。

找出導出矩陣C中最大項cij后，說明判斷矩陣A中對應的元素aij是造成不一致性最嚴重的元素，修改元素aij使得

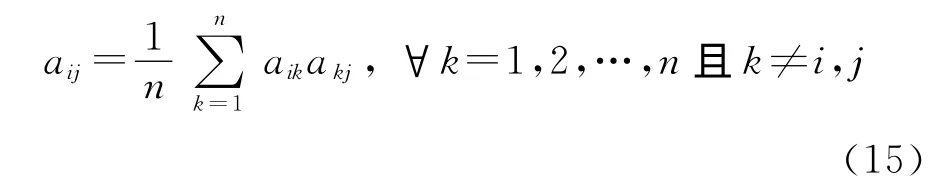
重新進行一致性判斷，若還不滿足一致性要求，繼續根據導出矩陣尋找不一致元素aij并修改，直至滿足一致性為止。求出判斷矩陣A的最大特征值λmax對應的歸一化特征向量Q＝（q1，…，qn），qi（i＝1，…，n）就是第i個指標的權重，Q就是這n個指標的權重向量。

按照表5判斷矩陣中各元素的均值和方差，隨機生成一個判斷矩陣表7。

表7 隨機生成判斷矩陣

利用Matlab的EIG函數求得上述矩陣的特征值和特征向量，最大特征值λmax＝4.0998，根據式（12）得CI＝0.0333，RI＝0.546，對應的CR＝0.061＜0.1，判斷矩陣滿足一致性，對應的歸一化特征向量為Q＝（0.0906 0.1919 0.3190 0.3985），權重向量Q的元素即為W6～W7對應的指標權重。

5 結語

考慮了自信度的專家打分法更能反映評估中的不確定性因素，利用合理的指數標度法對打分進行數量化，雖然基于自信度的判斷矩陣計算相對復雜一些，但是也能更好地反映評估指標間相對重要性關系的細微不確定性，本文通過嚴密的數學推導得出指標權重的算法，通過對被動雷達導引頭抗有源干擾指標的子指標間相對權重的計算，結果驗證了算法的有效性和準確性。

［1］楊莉，吳陽春，樊祥.對抗反輻射導彈技術分析［J］.探測與控制學報，2006，28（2）：53－56.

［2］風云.美國防空導彈概覽［J］.中國民兵，2005（2）：59－60.

［3］郭豫并，張慶祥，余波.雷達抗干擾效果評估方法探討［J］.雷達與對抗，2006（4）：1－3.

［4］李相平，李世忠，李亞昆.反艦導彈主被動雷達復合導引頭抗干擾性能評估研究［J］.雷達與對抗，2007（3）：8－12.

［5］同武勤.導引頭抗干擾性能評估［J］.現代雷達，2005，27（12）：61－64.

［6］劉軍，賈宏慧.模糊層次分析法在防空導彈武器系統效能分析中的應用［J］.計算機工程與設計，2007，28（16）：4049－4051.

［7］白普易，任明秋，王學軍.等.雷達抗干擾性能評估指標分析與測試平臺設計［J］.計算機與數字工程，2011，39（11）：25－29.

［8］邱鵬宇.反艦導彈復合導引頭抗干擾性能仿真研究［D］.長沙：國防科技大學，2005：12－14.

［9］劉興堂，吳曉燕.現代系統建模與仿真技術［M］.西安：西北工業大學出版社，2001，8：99－102.

［10］劉揚，水娟娜.某型艦空導彈武器系統驗收方案的優選［J］.海軍航空工程學院學報，2012（1）：747－751.